Fractals/Iterations in the complex plane/MandelbrotSetExterior/ParameterExternalRay

Parameter external ray

Tuning external ray

• DOUADY’S MAGIC FORMULA: Claude : "Douady's magic formula maps rays from the cardioid to the real axis by prefixing binary expansion with 10 or 01 depending if the angle is below or above 1/2. The paper involves veins and Hubbard trees"

landing

The Douady-Hubbard landing theorem for periodic external for a complex polynomial f with bounded postcritical set:

• every periodic external ray lands at a repelling or parabolic periodic point
• conversely every repelling or parabolic point is the landing point of at least one periodic external ray

Q&A

relation between parameter and dynamic rays

wake

Mandel demo 3 ( external ray) page 8

For a p-periodic angle, the corresponding dynamic ray of a connected Julia set lands at a repelling or parabolic point with period dividing p. The corresponding parameter ray lands at the root of a hyperbolic component with period p.

To show this, consider a parameter c0 where the parameter ray accumulates. For parameters c on this ray, the corresponding dynamic ray branches. If the dynamic ray for c0 landed at a repelling periodic point, it would land without branching also for c ≈ c0 by the Implicit Function Theorem and a pullback argument. This contradiction shows that the dynamic ray for the parameter c0 must land at a parabolic point, and c0 is a root.

In fact, exactly two parameter rays with periodic angles land at every root. This was shown

• by Adrien Douady and John Hamal Hubbard, using Fatou coordinates for the parabolic implosion (Chapter 2).
• Combinatorial proofs were given by Dierk Schleicher and John Milnor.

For parameters c in the wake between the two parameter rays:

• the two dynamic rays with the same angles land together,
• and the critical value z = c is always in the wake between them, even if there are more dynamic rays landing.

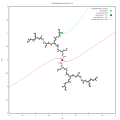
The left image shows the parameter rays with the 2-periodic angles 1/3 and 2/3, which land at the root of the period-2 component. The cross indicates the center c = -1.

The right image shows the corresponding filled Julia set, the "basilica," and the two dynamic rays landing at the repelling fixed point αc . The cross is at the critical value z = c. Now you shall see the Julia sets for the centers corresponding to the p-periodic angles 1/(2p-1) and 2/(2p-1), and all parameter rays with these denomiantors: Hit Return or push the Go-button to increase the period (2...9).

Subdivision rule

How to compute dynamic external rays that land on the critical point $z=0$ of the dendrite Julia set?

Steps:

• the preperiodic angle $\theta$ (decimal fraction with even denominator )
• find on the parameter plane the landing point of the parameter external ray $\theta$ which is Misiurewicz point: $\gamma _{M}(\theta )=c=M$
• on the dynamic plane:
  • landing point of the ray with angle $\theta$ is critical value: $z=c$
  • on the critical point z = 0 land rays with angles: $\theta /2$ and $(\theta +1)/2$

Examples of parameter rays:

• Ray for angle ${\frac {1}{2}}=0.0(1)$ lands on the point $c=\gamma _{M}(1/2)=-2=M_{1,1}$ from the parameter plane. It is tip of the main antenna ( end of 1/2 limb).
• Ray for angle ${\frac {1}{4}}=0.00(1)$ lands on the point $c=\gamma _{M}(1/4)=-0.228155493653962+1.115142508039937i=M_{2,1}$ from the parameter plane. It is the first tip of wake 1/3.
• Ray for angle ${\frac {1}{6}}=0.0(01)$ lands on the point $c=\gamma _{M}(1/6)=i=M_{1,2}$ from the parameter plane. It is the last tip of wake 1/3
• Ray for angle ${\frac {17}{240}}=0001(0010)$ lands on the point $c=\gamma _{M}(17/240)=0.366362983422764+0.591533773261445i=M_{4,4}$ from the parameter plane. It is the principle Misiurewicz point ( branch point or hub) of wake 1/4.
• Ray for angle ${\frac {9}{56}}=0.001(010)$ lands on the point $c=\gamma _{M}(9/56)=-0.101096363845622+0.956286510809142i=M_{3,3}$ from the parameter plane. It is the principle Misiurewicz point ( branch point or hub) of wake 1/3.
• Ray for angle ${\frac {129}{16256}}=0.0000001(0000010)$ lands on the point $c=\gamma _{M}(129/16256)=0.397391822296541+0.133511204871878i=M_{7,7}$ from the parameter plane. It is the principle Misiurewicz point ( branch point or hub) of wake 1/7.

Partition of the dynamic plane by dynamic rays is related with the kneading sequence

• 
  1/4
• 
  1/6
• 
  9/56
• 
  129/16256

principal Misiurewicz point rule

External rays of the wake and repelling fixed point on the dynamic plane

Notes from demo 3 (external rays) page 9/12 from program mandel by Wolf Jung

The parameter rays with the angles 1/7 and 2/7 land at the root of a period-3 component, which is of satellite type with rotation number 1/3.

For all parameters c in the wake between the rays

• for c in the 1/3-limb of the Mandelbrot set,
  • for c equal to the principle Misiurewicz point of the wake

the dynamic rays with the angles 1/7, 2/7, and 4/7:

• land together at the repelling fixed point $z=\alpha _{c}$
• the critical value z = c is between the first two rays.

We shall compute the external angles of certain preimages of fixed point alpha $z=\alpha _{c}$under $f_{c}(z)$.

Note that an angle $\theta$ has two preimages under doubling modulo 1, $(\theta /2,(\theta +1)/2)$.

Point $z=-\alpha _{c}$ is the only preimage of $z=\alpha _{c}$ different from the fixed point itself.

The angle 1/7 has the preimages (1/7)/2 = 1/14 and (1/7 + 1)/2 = 4/7. The latter angle belongs to $z=\alpha _{c}$, so 1/14 is an external angle of $z=-\alpha _{c}$ .

In the same way, the other angles 9/14 and 11/14 are obtained. The rays are drawn blue.

Move z to that preimage of $z=-\alpha _{c}$ between the rays for 2/7 and 4/7. The angle 1/14 has the preimages (1/14)/2 = 1/28 and (1/14 + 1)/2 = 15/28. Only the latter angle is in the chosen interval. The other two external angles of z are 9/28 and 11/28. The rays are drawn magenta.

Now z is the preimage between the rays for 1/7 and 2/7. By taking preimages in this interval, the external angles 9/56, 11/56, and 15/56 are obtained. The rays are drawn red.

Rays with preperiodic angles, i.e., even denominators, land at preperiodic points in the dynamic plane, or at Misiurewicz points in the parameter plane. For these parameters, the critcal value is preperiodic under the iteration of fc(z).

orbit of repelling fixed point alpha $z=\alpha _{c}$ has period 3

z	orbit portrait	description
-0.327586178699357 +0.577756453298949 i	(1/7, 2/7, 4/7)	repelling fixed point alpha $z=\alpha _{c}$
+0.327586178699356 -0.577756453298949 i	(1/14, 9/14, 11/14)	preimage: $z=b(\alpha _{c})=f^{-1}(\alpha _{c})=-\alpha _{c}$
-1.005359779818338 +0.762932332734299 i	(9/28, 11/28, 15/28 )	a(z)
-0.101096363845622 +0.956286510809142 i	(9/56, 11/56, and 15/56)	a(z)
-0.000000003174826 +0.000000002063599 i	(9/56, 11/56, and 15/56)	a(z) ; it should be critical point z = 0
-0.728941649258717 +0.655941740822478 i		a(z)
-0.184581740009785 +0.813582020547489 i		a(z)
-0.202294024682997 +0.352715534938011 i		a(z)
-0.505370243253601 +0.597157217578291 i		a(z)
-0.261224737974777 +0.687395259758146 i		a(z)
-0.276433581450372 +0.486357789166200 i		a(z)

symbolic dynamic

• Symbolic Dynamics of Quadratic Polynomials. Version of July 27, 2011. Henk Bruin, Alexandra Kaffl and Dierk Schleicher
  • long version
  • short version

idea

• take a segment of straight ray ( near infinity )
• pull it back toward boundary of Mandelbrot set

How to aproximate external rays?

• binary decomposition method for Julia set ( BDM/J)
• field lines of the scalar field ( potential)
• SAM = Stripe Average Method is basically a cheap way to calculate an angle.

• 
  BDM , some rays can be seen
• 
  boundaries of BDM
• 
  field lines
• 
  SAM

In BDM images the external rays of angles (measured in turns):

$angle=(k/2^{n})~~{\mbox{mod }}~1\,$

can be seen as borders of subsets.

What means to draw external ray ?

It means:

• calculate (approximate) DS points of ray. The result is the set of complex numbers $\{c_{m}:1\leq m\leq DS\}$ ( points on the parameter plane ), use numerical algotrithm
• join points by line segments, use graphical algorithm )

This will give an approximation of ray ${\mathcal {R}}$.

trace an external ray for angle t in turns, which means ( description by Claude Heiland-Allen)

• starting at a large circle (e.g. r = 65536, x = r cos(2 pi t), y = r sin(2 pi t))
• following the escape lines (like the edges of binary decomposition colouring with large escape radius) in towards the Mandelbrot set.

this algorithm is O(period^2), which means doubling the period takes 4x as long, so it's only really feasible for periods up to a few 1000.

How to compute one point of the ray ?

By solving polynomial equation

  $P_{m}(c)=0$

with numerical methods. The root of above equation is point $c_{m}$.

 $c_{m}=c:P_{m}(c)=0$

It is a point of the external parameter ray ${\mathcal {R}}(\theta )$

 $\arg(\Phi _{M}(c_{m}))=\theta$

or

 $c_{m}\in {\mathcal {R}}(\theta )$

Using Newton method ( iteration ) one can compute approximation of point $c_{m}$

What one needs to start :

• arbitrarily chosen external angle $\theta$ of the ray $R(\theta )$ one wants to draw. Angle is usually given in turns
• value of function P ( which approximates Boettcher mapping ) and its derivative P'
• starting point $c_{m,0}$ ( initial approximation )
• stopping rule ( criteria to stop iteration ): Ray tracing has a natural stopping condition: when the ray enters the atom domain with period p, Newton's method is very likely to converge to the nucleus at its center.

When ray lands ?

"The rays get closer and closer to the boundary, but don't reach it in finite time - for a more exact boundary point you need to switch to different methods when the ray is close enough. For points on the boundary of hyperbolic components, split the internal angled address (computable from the angle) into island and child path components, when tracing the ray to the parent island use atom domain test (to see if Newton's method is likely to converge to the right place) and switch to Newton's method to find the nucleus of the parent island and then trace internal rays through the chain of connected components to the desired boundary point.

For Misiurewicz points, there is probably a similar test to the atom domain test after which point Newton's method will converge to the desired location (though rays to Misiurewicz points tend to converge much more quickly than rays to roots of hyperbolic components anyway). The atom domain test checks that the iteration count of the last minimum of |z| is the same as the period of the ray." Claude Heiland-Allen

So ray does not "land" in the finite time. Landing point can be denoted as $c_{\infty }$

Algorithms

• Jungreis-Ewing-Schober (JES) algorithm (based on the Laurent series expansion about infinity for $\Phi _{M}^{-1}\,$)
• OTIS method ( based on the Newton method)

tracing rays

• outwards: "External Rays of the form 2pi*n/32, on top of the modulus of the potential gradient. For each point c, a path is created that follows the direction of the gradient of the potential. Each step size is proportional to the distance estimation to M. When the point is far enough of M, it's phase aproximates the phase of phi(c)." Inigo Quilez
• inwards : "The drawing method : ... the path is followed in reverse order: from the infinity towards M, following the minus gradient."

Tracing ray

• inwards = from infinity towards Mandelbrot set
• outwards = from point near Mandelbrot set towards infinity

Collecting bits of external angle's binary expansion when crossing dwell bands ( boundaries of level sets):

• inwards: add bit at the end of binary expansion
• outwards: add the bit at the beginning of binary expansion

crossing dwell bands ( boundaries of level sets)

• when ray value is changing it's integer part

See also

• binary decomposition
  • parameter plane
  • dynamic plane
• reading bits from binary decomposition = collecting bits of external angle's binary expansion

in

• When tracing inwards, one peels off the most-significant bit (aka angle doubling) each time the ray crosses a dwell band (integer part of normalized iteration count increases by 1).

trace an external ray for angle t in turns, which means ( description by Claude Heiland-Allen)

• starting at a large circle (e.g. r = 65536, x = r cos(2 pi t), y = r sin(2 pi t))
• following the escape lines (like the edges of binary decomposition colouring with large escape radius) in towards the Mandelbrot set.

this algorithm is O(period^2), which means doubling the period takes 4x as long, so it's only really feasible for periods up to a few 1000.

out

External angle of the ray: image is showing how the bits of external angle's binary expansion are collected. When tracing a ray outwards: add the bit at begining

 "you need to trace a ray outwards, which means using different C values, and the bits come in reverse order, first the deepest bit from the iteration count of the start pixel, then move C outwards along the ray (perhaps using the newton's method of mandel-exray.pdf in reverse), repeat until no more bits left.  you move C a fractional iteration count each time, and collect bits when crossing integer dwell boundaries" Claude Heiland-Allen

Newton method

• using Newton method
• description by Tomoki Kawahira
• tracing inward ( from infinity toward Mandelbrot set) = ray-in
• arbitrary precision ( mpfr) with dynamic precision adjustment by Claude Heiland-Allen

variables

• r = radial parameter = radius ( see complex potential )
• m = radial index = index of point along ray, integer
• j = sharpness = number of points on the dwell band, integer
• k = integer depth = number of dwell bands, integer
• d = m/S = real depth, floating point number ( name d is not used by Kawahira)
• l = index of Newton iteration ( name l is not used by Kawahira)
• n = index of iteration for computing Newton map

Names are from T Kawahira description

constant values

• S = $j_{max}$ =
• D = $k_{max}$ =
• R = ER = Escape Radius
• DS = $m_{max}$ = number of points
• $L=L_{m}=l_{m,max}$

ranges

• sharpness : $1\leq j\leq S$
• radial index : $1\leq m\leq DS$
• depth :
  • $1\leq k\leq D$
  • $1\leq d\leq D$
• ray's radius ( subset): $R^{1/2^{D}}\leq r<R$
• iterations :
  • quadratic : $1\leq n\leq k$
  • Newton : $1\leq l_{m}\leq L_{m}$

sequences

m-sequences ( along the ray toward the Mandelbrot set):

• $r_{1},r_{2},\cdots ,r_{SD}$
• $t_{1},t_{2},\cdots ,t_{SD}$
• $c_{1},c_{2},\cdots ,c_{SD}$

Newton sequences = l-sequences, here m is constant:

• from initial value $c_{m,0}$ toward an approximation of $c_{m,L}$
• $c_{m,0},c_{m,1},\cdots ,c_{m,L}$

  $c_{m,0}{\xrightarrow {N}}c_{m,1}{\xrightarrow {N}}c_{m,1}{\xrightarrow {N}}\cdots {\xrightarrow {N}}c_{m,L}$

Maps

r map

 $r_{m}=R^{1/2^{d}}$

compare it with inverse iteration on c=0 dynamic plane

Depth

Using fixed integer D (maximal depth ) :

$k_{max}=D>1$

and fixed maximal value of radial parameter ( escape radius = ER ) :

$r_{max}=R>1$

one can compute D points of ray using formula :

$r=R^{1/2^{k}}$

which is :

$1<R^{1/2^{D}}<=r<=R$

When $k\to k_{max}=D\$ then $r\to 1$ and radius reaches enough close to the boundary of Mandelbrot set

/*
Maxima CAS code

Number of ray points = depth  
r = radial parametr : 1 < R^{1/{2^D}} <= r > ER  
*/

GiveRadius( depth):=
block (
 [ r, R: 65536],
 r:R,
 print("r = ER = ", float(R)),

 for k:1   thru depth  do
   (
     r:er^(1/(2^k)),
     print("k = ", k, " r = ", float(r))
    )
)$

compile(all)$

/* --------------------------- */

GiveRadius(10)$

Output :

r = ER =  65536.0 
"k = "1"  r = "256.0
"k = "2"  r = "16.0
"k = "3"  r = "4.0
"k = "4"  r = "2.0
"k = "5"  r = "1.414213562373095
"k = "6"  r = "1.189207115002721
"k = "7"  r = "1.090507732665258
"k = "8"  r = "1.044273782427414
"k = "9"  r = "1.021897148654117
"k = "10" r = "1.0108892860517

Depth and sharpness

How to make ray more smooth ? Add more points between level sets.

Using:

• fixed integer S =maximal sharpness
• fixed integer D = maximal depth

 $S>0$

one can compute S*D points of ray using fomula :

 $m=m_{S}(j,k)=(k-1)S+j$
 $d=d_{S}(j,k)=d_{S}(m)={\frac {m}{S}}=(k-1)+{\frac {j}{S}}$

Note that k is equal to integer part of d :

 $k=int(d)$

and last point is the same as in depth method

  $r_{d_{max}}=r_{k_{max}}$

but there are more points here because :

 $S*D>D$

/* Maxima CAS code */
kill(all);
remvalue(all);

GiveRadius(  depth, sharpness):=
block (
 [ r, R: 65536, d ],
 
 r:R,
 
 print("r = ER = ", float(R)),

 for k:1   thru depth  do
   (
     for j:1   thru sharpness  do
      (  d: (k-1) + j/sharpness,
         r:R^(1/(2^d)),
         print("k = ", k, " ; j = ", j , "; d = ", float(d), "; r = ", float(r))
      )
    )
)$

compile(all)$

/* --------------------------- */

GiveRadius( 10, 4)$
compile(all)$

Output :

r = ER =  65536.0 
k =  1  ; j =  1 ; d =  0.25 ; r =  11224.33726645605 
k =  1  ; j =  2 ; d =  0.5 ; r =  2545.456152628088 
k =  1  ; j =  3 ; d =  0.75 ; r =  730.9641900482128 
k =  1  ; j =  4 ; d =  1.0 ; r =  256.0 
k =  2  ; j =  1 ; d =  1.25 ; r =  105.9449728229521 
k =  2  ; j =  2 ; d =  1.5 ; r =  50.45251383854013 
k =  2  ; j =  3 ; d =  1.75 ; r =  27.0363494216252 
k =  2  ; j =  4 ; d =  2.0 ; r =  16.0 
k =  3  ; j =  1 ; d =  2.25 ; r =  10.29295743812011 
k =  3  ; j =  2 ; d =  2.5 ; r =  7.10299330131601 
k =  3  ; j =  3 ; d =  2.75 ; r =  5.199648971000369 
k =  3  ; j =  4 ; d =  3.0 ; r =  4.0 
k =  4  ; j =  1 ; d =  3.25 ; r =  3.208263928999625 
k =  4  ; j =  2 ; d =  3.5 ; r =  2.665144142690224 
k =  4  ; j =  3 ; d =  3.75 ; r =  2.280273880699502 
k =  4  ; j =  4 ; d =  4.0 ; r =  2.0 
k =  5  ; j =  1 ; d =  4.25 ; r =  1.791162731021284 
k =  5  ; j =  2 ; d =  4.5 ; r =  1.632526919438152 
k =  5  ; j =  3 ; d =  4.75 ; r =  1.51005757529291 
k =  5  ; j =  4 ; d =  5.0 ; r =  1.414213562373095 
k =  6  ; j =  1 ; d =  5.25 ; r =  1.338343278468302 
k =  6  ; j =  2 ; d =  5.5 ; r =  1.277703768264832 
k =  6  ; j =  3 ; d =  5.75 ; r =  1.228843999575581 
k =  6  ; j =  4 ; d =  6.0 ; r =  1.189207115002721 
k =  7  ; j =  1 ; d =  6.25 ; r =  1.156867874248526 
k =  7  ; j =  2 ; d =  6.5 ; r =  1.13035559372475 
k =  7  ; j =  3 ; d =  6.75 ; r =  1.108532362890494 
k =  7  ; j =  4 ; d =  7.0 ; r =  1.090507732665258 
k =  8  ; j =  1 ; d =  7.25 ; r =  1.075577925697867 
k =  8  ; j =  2 ; d =  7.5 ; r =  1.063181825335982 
k =  8  ; j =  3 ; d =  7.75 ; r =  1.052868635153737 
k =  8  ; j =  4 ; d =  8.0 ; r =  1.044273782427414 
k =  9  ; j =  1 ; d =  8.25 ; r =  1.037100730738276 
k =  9  ; j =  2 ; d =  8.5 ; r =  1.031107087230023 
k =  9  ; j =  3 ; d =  8.75 ; r =  1.026093872486205 
k =  9  ; j =  4 ; d =  9.0 ; r =  1.021897148654117 
k =  10  ; j =  1 ; d =  9.25 ; r =  1.018381426940945 
k =  10  ; j =  2 ; d =  9.5 ; r =  1.015434432757735 
k =  10  ; j =  3 ; d =  9.75 ; r =  1.012962917626408 
k =  10  ; j =  4 ; d =  10.0 ; r =  1.0108892860517 

m

One can use only one loop : m-loop and ccompute j,k and d from m

/* Maxima CAS code */
kill(all);
remvalue(all)$

GiveRadius( depth, sharpness):=
block (
 [ r, R: 65536, j, k, d, mMax ],
 
 r:float(R),
 mMax:depth*sharpness,
 
 print("r = ER = ", r),
 print( "m k j  r"),

 for m:1   thru mMax  do
   (
      d: m/sharpness,
      r:float(R^(1/(2^d))),

      k: floor(d),
      j: m - k*sharpness ,

      print( m, k, j, r)
     
    )
)$

compile(all)$

/* --------------------------- */

GiveRadius( 10, 4)$

output :

r = ER =  65536.0 
m k j r 
1 0 1 11224.33726645605 
2 0 2 2545.456152628088 
3 0 3 730.9641900482128 
4 1 0 256.0 
5 1 1 105.9449728229521 
6 1 2 50.45251383854013 
7 1 3 27.0363494216252 
8 2 0 16.0 
9 2 1 10.29295743812011 
10 2 2 7.10299330131601 
11 2 3 5.199648971000369 
12 3 0 4.0 
13 3 1 3.208263928999625 
14 3 2 2.665144142690224 
15 3 3 2.280273880699502 
16 4 0 2.0 
17 4 1 1.791162731021284 
18 4 2 1.632526919438152 
19 4 3 1.51005757529291 
20 5 0 1.414213562373095 
21 5 1 1.338343278468302 
22 5 2 1.277703768264832 
23 5 3 1.228843999575581 
24 6 0 1.189207115002721 
25 6 1 1.156867874248526 
26 6 2 1.13035559372475 
27 6 3 1.108532362890494 
28 7 0 1.090507732665258 
29 7 1 1.075577925697867 
30 7 2 1.063181825335982 
31 7 3 1.052868635153737 
32 8 0 1.044273782427414 
33 8 1 1.037100730738276 
34 8 2 1.031107087230023 
35 8 3 1.026093872486205 
36 9 0 1.021897148654117 
37 9 1 1.018381426940945 
38 9 2 1.015434432757735 
39 9 3 1.012962917626408 
40 10 0 1.0108892860517 

Polynomial map q

Complex quadratic polynomial :

 $q_{c}(z)=z^{2}+c$

iteration :

 $q_{c}^{n}(z)={q_{c}^{n-1}(z)}^{2}+c$

Map t

   $t_{m}=t_{m}(r,\theta ):=r_{m}^{2^{k}}e^{2\pi i2^{k}\theta }$

compare it with forward iteration on c=0 plane :

 $z=r_{m}e^{2\pi i\theta }$

 $q_{0}^{k}(z_{m})$

Polynomial map P

P is a polynomial of degree $2^{k}$ in variable c.

 $P_{m}(c):=q_{c}^{k}(c)-t_{m}$

Derivative with respect to c :

 $P'_{m}(c):={\frac {dP_{m}(c)}{dc}}=2P'_{m-1}(c)P_{k-m}(c)+1$

Newton map N

Newton map:

 $N_{m}(c_{l})=c_{l}-{\frac {P_{m}(c_{l})}{P'_{m}(c_{l})}}$

note that here :

  $c_{l}=c_{m,l}$

How to compute new value $c_{m,l+1}$ ?

• start with $c_{m,l}$
• compute value $t_{m}$ ( without iteration )
• compute $C_{n}$ and $D_{n}$ using quadratic iteration from n=1 to n=k
• compute next point $c_{m,l+1}$ using one Newton iteration

Arbitrary names :

  $C_{n}:=q^{n}(c_{m,l})$ 
  $D_{n}:=P'_{n}(c_{m,l})=(q^{n}(c_{m,l})-t)'=(q^{n}(c_{m,l}))'$

Note that the derivative of a constant is zero.

The recursive formulae and initial values:

 $C_{n}=C_{n-1}^{2}+c_{m,l};\qquad \qquad C_{1}=c_{m,l}$ 
 $D_{n}=2C_{n-1}D_{n-1}+1;\qquad D_{1}=1$

After k quadratic iterations compute new value $c_{m,l+1}$ using one Newton iteration

 $c_{m,l+1}=N_{m}(c_{m,l})=c_{m,l}-{\frac {C_{k}-t_{m}}{D_{k}}}$

It is implemented in :

• mandelbrot-numerics library
  • c/lib/m_d_exray_in_step = double precision
  • c/lib/m_r_exray_in.c = mpfr ( arbitrary precision)

Newton iteration

Formula :

 $c_{m,l+1}:=N(c_{m,l})$

Newton iterations gives Newton sequence ( = l-sequence, here m is constant):

• from initial value $c_{m,0}$ toward an approximation of $c_{m,L}$
• $c_{m,0},c_{m,1},\cdots ,c_{m,L}$

Sequence :

  $c_{m,0}{\xrightarrow {N}}c_{m,1}{\xrightarrow {N}}c_{m,1}{\xrightarrow {N}}\cdots {\xrightarrow {N}}c_{m,L}$

Initial points

• $c_{1,0}=Re^{2\pi i\theta }$
• The value $c_{m-1,L}$ is presumably a “neighbor” of $c_{m,L}$ on ray so use it as the initial value for $c_{m}$ which is $c_{m,0}$

  $c_{m,0}=c_{m-1,L}$

Code

• c code by Claude Heiland-Allen
  • book console program and gui version, uses stream
  • mandelbrot-numerics library
  • mandelbrot perturbator GUI program
• newtonRay - cpp code from program Mandel by Wolf Jung
• sage
  • description by Ben Barros
  • mandel_julia.py = python code at git repo by Ben Barros
  • mandel_julia_helper.pyx
  • final-report
  • Sage Reference Manual: Discrete dynamics Release 8.3
• The Mandelbrot capacitor with field lines by Nils Berglund and c code : heat.c

c code

mpfr

Code for computing external ray inwards using Newton method based on the mandelbrot-book code by Claude Heiland-Allen

External angle is read from the string ( binary fraction)

/*

code is from : 
https://code.mathr.co.uk/mandelbrot-book
mandelbrot-book/code/examples/ray-in.sh
mandelbrot-book/code/examples/ray-in.c
mandelbrot-book/code/bin/mandelbrot_external_ray_in.c
mandelbrot-book/code/lib/mandelbrot_external_ray_in.c
mandelbrot-book/code/lib/mandelbrot_external_ray_in.h
mandelbrot-book/code/lib/mandelbrot_external_ray_in_native.c
mandelbrot-book/code/lib/mandelbrot_external_ray_in_native.h
mandelbrot-book/code/lib/mandelbrot_binary_angle.c
mandelbrot-book/code/lib/mandelbrot_binary_angle.h
mandelbrot-book/code/lib/pi.c
mandelbrot-book/code/lib/pi.h


--------------------------------------------------------

gcc r.c -std=c99 -Wall -Wextra -pedantic -lm -lgmp -lmpfr
./a.out



*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <complex.h>
#include <gmp.h>
#include <mpfr.h>
#include <stdbool.h>



const float pif = 3.14159265358979323846264338327950288419716939937510f;
const double pi = 3.14159265358979323846264338327950288419716939937510;
const long double pil = 3.14159265358979323846264338327950288419716939937510l;



// ------------------------------------------------------------
struct mandelbrot_binary_angle {
  int preperiod;
  int period;
  char *pre;
  char *per;
};

struct mandelbrot_external_ray_in {
  mpq_t angle;
  mpq_t one;
  unsigned int sharpness; // number of steps to take within each dwell band
  unsigned int precision; // delta needs this many bits of effective precision
  unsigned int accuracy;  // epsilon is scaled relative to magnitude of delta
  double escape_radius;
  mpfr_t epsilon2;
  mpfr_t cx;
  mpfr_t cy;
  unsigned int j;
  unsigned int k;
  // temporaries
  mpfr_t zx, zy, dzx, dzy, ux, uy, vx, vy, ccx, ccy, cccx, cccy;
};


// ----------------------------------------------------------------------------



int depth = 0;
mpq_t angle;
int base = 2; // The base can vary from 2 to 62, or if base is 0 then the leading characters are used: 0x or 0X for hex, 0b or 0B for binary, 0 for octal, or decimal otherwise.
char *s;
struct mandelbrot_binary_angle *a ;
mpfr_t cre, cim;

struct mandelbrot_external_ray_in *ray; //  = mandelbrot_external_ray_in_new(angle);


// ----------------------------------------------------------------------------
void mandelbrot_binary_angle_delete(struct mandelbrot_binary_angle *a) {
  free(a->pre);
  free(a->per);
  free(a);
}



// FIXME check canonical form, ie no .01(01) etc
struct mandelbrot_binary_angle *mandelbrot_binary_angle_from_string(const char *s) {
  const char *dot = strchr(s,   '.');
  if (! dot) { return 0; }
  const char *bra = strchr(dot, '(');
  if (! bra) { return 0; }
  const char *ket = strchr(bra, ')');
  if (! ket) { return 0; }
  if (s[0] != '.') { return 0; }
  if (ket[1] != 0) { return 0; }
  struct mandelbrot_binary_angle *a = malloc(sizeof(struct mandelbrot_binary_angle));
  a->preperiod = bra - dot - 1;
  a->period = ket - bra - 1;
  fprintf( stderr	, "external angle \n");
  fprintf( stderr	, "\thas preperiod = %d \t period = %d\n",  a->preperiod,  a->period);
  
  if (a->period < 1) {
    free(a);
    return 0;
  }
  a->pre = malloc(a->preperiod + 1);
  a->per = malloc(a->period + 1);
  memcpy(a->pre, dot + 1, a->preperiod);
  memcpy(a->per, bra + 1, a->period);
  a->pre[a->preperiod] = 0;
  a->per[a->period] = 0;
  for (int i = 0; i < a->preperiod; ++i) {
    if (a->pre[i] != '0' && a->pre[i] != '1') {
      mandelbrot_binary_angle_delete(a);
      return 0;
    }
  }
  for (int i = 0; i < a->period; ++i) {
    if (a->per[i] != '0' && a->per[i] != '1') {
      mandelbrot_binary_angle_delete(a);
      return 0;
    }
  }
  return a;
}


void mandelbrot_binary_angle_to_rational(mpq_t r, const struct mandelbrot_binary_angle *t) {
  mpq_t pre, per;
  mpq_init(pre);
  mpq_init(per);
  mpz_set_str(mpq_numref(pre), t->pre, 2);
  mpz_set_si(mpq_denref(pre), 1);
  mpz_mul_2exp(mpq_denref(pre), mpq_denref(pre), t->preperiod);
  mpq_canonicalize(pre);
  mpz_set_str(mpq_numref(per), t->per, 2);
  mpz_set_si(mpq_denref(per), 1);
  mpz_mul_2exp(mpq_denref(per), mpq_denref(per), t->period);
  mpz_sub_ui(mpq_denref(per), mpq_denref(per), 1);
  mpz_mul_2exp(mpq_denref(per), mpq_denref(per), t->preperiod);
  mpq_canonicalize(per);
  mpq_add(r, pre, per);
  mpq_clear(pre);
  mpq_clear(per);
}

// -------------------------------------------------------------

struct mandelbrot_external_ray_in *mandelbrot_external_ray_in_new(mpq_t angle) {
  struct mandelbrot_external_ray_in *r = malloc(sizeof(struct mandelbrot_external_ray_in));
  mpq_init(r->angle);
  mpq_set(r->angle, angle);
  mpq_init(r->one);
  mpq_set_ui(r->one, 1, 1);
  r->sharpness = 4;
  r->precision = 4;
  r->accuracy  = 4;
  r->escape_radius = 65536.0;
  mpfr_init2(r->epsilon2, 53);
  mpfr_set_ui(r->epsilon2, 1, GMP_RNDN);
  double a = 2.0 * pi * mpq_get_d(r->angle);
  mpfr_init2(r->cx, 53);
  mpfr_init2(r->cy, 53);
  mpfr_set_d(r->cx, r->escape_radius * cos(a), GMP_RNDN);
  mpfr_set_d(r->cy, r->escape_radius * sin(a), GMP_RNDN);
  r->k = 0;
  r->j = 0;
  // initialize temporaries
  mpfr_inits2(53, r->zx, r->zy, r->dzx, r->dzy, r->ux, r->uy, r->vx, r->vy, r->ccx, r->ccy, r->cccx, r->cccy, (mpfr_ptr) 0);
  return r;
}

int mandelbrot_external_ray_in_step(struct mandelbrot_external_ray_in *r) {
  if (r->j >= r->sharpness) {
    mpq_mul_2exp(r->angle, r->angle, 1);
    if (mpq_cmp_ui(r->angle, 1, 1) >= 0) {
      mpq_sub(r->angle, r->angle, r->one);
    }
    r->k++;
    r->j = 0;
  }
  // r0 <- er ** ((1/2) ** ((j + 0.5)/sharpness))
  // t0 <- r0 cis(2 * pi * angle)
  double r0 = pow(r->escape_radius, pow(0.5, (r->j + 0.5) / r->sharpness));
  double a0 = 2.0 * pi * mpq_get_d(r->angle);
  double t0x = r0 * cos(a0);
  double t0y = r0 * sin(a0);
  // c <- r->c
  mpfr_set(r->ccx, r->cx, GMP_RNDN);
  mpfr_set(r->ccy, r->cy, GMP_RNDN);
  for (unsigned int i = 0; i < 64; ++i) { // FIXME arbitrary limit
    // z <- 0
    // dz <- 0
    mpfr_set_ui(r->zx, 0, GMP_RNDN);
    mpfr_set_ui(r->zy, 0, GMP_RNDN);
    mpfr_set_ui(r->dzx, 0, GMP_RNDN);
    mpfr_set_ui(r->dzy, 0, GMP_RNDN);
    // iterate
    for (unsigned int p = 0; p <= r->k; ++p) {
      // dz <- 2 z dz + 1
      mpfr_mul(r->ux, r->zx, r->dzx, GMP_RNDN);
      mpfr_mul(r->uy, r->zy, r->dzy, GMP_RNDN);
      mpfr_mul(r->vx, r->zx, r->dzy, GMP_RNDN);
      mpfr_mul(r->vy, r->zy, r->dzx, GMP_RNDN);
      mpfr_sub(r->dzx, r->ux, r->uy, GMP_RNDN);
      mpfr_add(r->dzy, r->vx, r->vy, GMP_RNDN);
      mpfr_mul_2ui(r->dzx, r->dzx, 1, GMP_RNDN);
      mpfr_mul_2ui(r->dzy, r->dzy, 1, GMP_RNDN);
      mpfr_add_ui(r->dzx, r->dzx, 1, GMP_RNDN);
      // z <- z^2 + c
      mpfr_sqr(r->ux, r->zx, GMP_RNDN);
      mpfr_sqr(r->uy, r->zy, GMP_RNDN);
      mpfr_sub(r->vx, r->ux, r->uy, GMP_RNDN);
      mpfr_mul(r->vy, r->zx, r->zy, GMP_RNDN);
      mpfr_mul_2ui(r->vy, r->vy, 1, GMP_RNDN);
      mpfr_add(r->zx, r->vx, r->ccx, GMP_RNDN);
      mpfr_add(r->zy, r->vy, r->ccy, GMP_RNDN);
    }
    // c' <- c - (z - t0) / dz
    mpfr_sqr(r->ux, r->dzx, GMP_RNDN);
    mpfr_sqr(r->uy, r->dzy, GMP_RNDN);
    mpfr_add(r->vy, r->ux, r->uy, GMP_RNDN);
    mpfr_sub_d(r->zx, r->zx, t0x, GMP_RNDN);
    mpfr_sub_d(r->zy, r->zy, t0y, GMP_RNDN);
    mpfr_mul(r->ux, r->zx, r->dzx, GMP_RNDN);
    mpfr_mul(r->uy, r->zy, r->dzy, GMP_RNDN);
    mpfr_add(r->vx, r->ux, r->uy, GMP_RNDN);
    mpfr_div(r->ux, r->vx, r->vy, GMP_RNDN);
    mpfr_sub(r->cccx, r->ccx, r->ux, GMP_RNDN);
    mpfr_mul(r->ux, r->zy, r->dzx, GMP_RNDN);
    mpfr_mul(r->uy, r->zx, r->dzy, GMP_RNDN);
    mpfr_sub(r->vx, r->ux, r->uy, GMP_RNDN);
    mpfr_div(r->uy, r->vx, r->vy, GMP_RNDN);
    mpfr_sub(r->cccy, r->ccy, r->uy, GMP_RNDN);
    // delta^2 = |c' - c|^2
    mpfr_sub(r->ux, r->cccx, r->ccx, GMP_RNDN);
    mpfr_sub(r->uy, r->cccy, r->ccy, GMP_RNDN);
    mpfr_sqr(r->vx, r->ux, GMP_RNDN);
    mpfr_sqr(r->vy, r->uy, GMP_RNDN);
    mpfr_add(r->ux, r->vx, r->vy, GMP_RNDN);
    // enough_bits = 0 < 2 * prec(eps^2) + exponent eps^2 - 2 * precision
    int enough_bits = 0 < 2 * (mpfr_get_prec(r->epsilon2) - r->precision) + mpfr_get_exp(r->epsilon2);
    if (enough_bits) {
      // converged = delta^2 < eps^2
      int converged = mpfr_less_p(r->ux, r->epsilon2);
      if (converged) {
        // eps^2 <- |c' - r->c|^2 >> (2 * accuracy)
        mpfr_sub(r->ux, r->cccx, r->cx, GMP_RNDN);
        mpfr_sub(r->uy, r->cccy, r->cy, GMP_RNDN);
        mpfr_sqr(r->vx, r->ux, GMP_RNDN);
        mpfr_sqr(r->vy, r->uy, GMP_RNDN);
        mpfr_add(r->ux, r->vx, r->vy, GMP_RNDN);
        mpfr_div_2ui(r->epsilon2, r->ux, 2 * r->accuracy, GMP_RNDN);
        // j <- j + 1
        r->j = r->j + 1;
        // r->c <- c'
        mpfr_set(r->cx, r->cccx, GMP_RNDN);
        mpfr_set(r->cy, r->cccy, GMP_RNDN);
        return 1;
      }
    } else {
      // bump precision
      mpfr_prec_t prec = mpfr_get_prec(r->cx) + 32;
      mpfr_prec_round(r->cx, prec, GMP_RNDN);
      mpfr_prec_round(r->cy, prec, GMP_RNDN);
      mpfr_prec_round(r->epsilon2, prec, GMP_RNDN);
      mpfr_set_prec(r->ccx, prec);
      mpfr_set_prec(r->ccy, prec);
      mpfr_set_prec(r->cccx, prec);
      mpfr_set_prec(r->cccy, prec);
      mpfr_set_prec(r->zx, prec);
      mpfr_set_prec(r->zy, prec);
      mpfr_set_prec(r->dzx, prec);
      mpfr_set_prec(r->dzy, prec);
      mpfr_set_prec(r->ux, prec);
      mpfr_set_prec(r->uy, prec);
      mpfr_set_prec(r->vx, prec);
      mpfr_set_prec(r->vy, prec);
      i = 0;
      // c <- r->c
      mpfr_set(r->cccx, r->cx, GMP_RNDN);
      mpfr_set(r->cccy, r->cy, GMP_RNDN);
    }
    mpfr_set(r->ccx, r->cccx, GMP_RNDN);
    mpfr_set(r->ccy, r->cccy, GMP_RNDN);
  }
  return 0;
}

void mandelbrot_external_ray_in_get(struct mandelbrot_external_ray_in *r, mpfr_t x, mpfr_t y) {
  mpfr_set_prec(x, mpfr_get_prec(r->cx));
  mpfr_set(x, r->cx, GMP_RNDN);
  mpfr_set_prec(y, mpfr_get_prec(r->cy));
  mpfr_set(y, r->cy, GMP_RNDN);
}



void mandelbrot_external_ray_in_delete(struct mandelbrot_external_ray_in *r) {
  mpfr_clear(r->epsilon2);
  mpfr_clear(r->cx);
  mpfr_clear(r->cy);
  mpq_clear(r->angle);
  mpq_clear(r->one);
  mpfr_clears(r->zx, r->zy, r->dzx, r->dzy, r->ux, r->uy, r->vx, r->vy, r->ccx, r->ccy, r->cccx, r->cccy, (mpfr_ptr) 0);
  free(r);
}

// -------------------------------------------------------------------------------------------------------

void PrintCInfo (void)
{

  fprintf(stderr,"gcc version: %d.%d.%d\n", __GNUC__, __GNUC_MINOR__, __GNUC_PATCHLEVEL__);	// https://stackoverflow.com/questions/20389193/how-do-i-check-my-gcc-c-compiler-version-for-my-eclipse
  // OpenMP version is displayed in the console : export  OMP_DISPLAY_ENV="TRUE"

  fprintf(stderr,"__STDC__ = %d\n", __STDC__);
  fprintf(stderr,"__STDC_VERSION__ = %ld\n", __STDC_VERSION__);
  fprintf(stderr,"c dialect = ");
  switch (__STDC_VERSION__)
    {				// the format YYYYMM 
    case 199409L:
      fprintf(stderr,"C94\n");
      break;
    case 199901L:
      fprintf(stderr,"C99\n");
      break;
    case 201112L:
      fprintf(stderr,"C11\n");
      break;
    case 201710L:
      fprintf(stderr,"C18\n");
      break;
      //default : /* Optional */
      }
      //gmp_printf (" GMP-%s \n ", gmp_version );
      mpfr_printf("Versions: MPFR-%s \n GMP-%s \n", mpfr_version, gmp_version );

    

}

void PrintInfo(void){

	//
	fprintf(stderr, "console C program  ( CLI ) for computing external ray of Mandelbrot set (parametric ray)\n"); 
	fprintf(stderr, "using Newton method described by Tomoki Kawahira \n"); 
	fprintf(stderr, "tracing inward ( from infinity toward Mandelbrot set) = ray-in\n"); 
	fprintf(stderr, "arbitrary precision (gmp, mpfr) with dynamic precision adjustment.\n Based on the code by Claude Heiland-Allen: https://mathr.co.uk/web/\n"); 
	fprintf(stderr, "usage: ./a.out angle depth\n outputs space-separated complex numbers on stdout\n example command \n./a.out 1/3 25\n or\n ./a.out .(01) 25\n");
	fprintf( stderr	, "\n");
  	fprintf( stderr	, "\tsharpness = %d\n", ray->sharpness);
  	fprintf( stderr	, "\tprecision = %d\n", ray->precision);
  	fprintf( stderr	, "\taccuracy = %d\n", ray->accuracy);
  	fprintf( stderr	, "\tescape_radius = %.0f\n", ray->escape_radius);
	// 
	PrintCInfo();
}


int setup(void){
	// 2 parameters of external ray : depth, angle
	depth  = 35;
	// external angle 
	s = ".(01)";  // landing point c = -0.750000000000000  +0.000000000000000 i    period = 10000
	// mpq
	mpq_init(angle);
	// mpq init from string or 2 integers
	
	a = mandelbrot_binary_angle_from_string(s); // set a from string 
	// gmp_fprintf (stderr, "\tas a binary fraction = %0b\n", a); // 0b or 0B for binary // not works
    	if (a) {
      		mandelbrot_binary_angle_to_rational(angle, a); // convert binary string to decimal rational number
      		mandelbrot_binary_angle_delete(a); } // use only rational form so delete string form
		
	mpq_canonicalize (angle); // It is the responsibility of the user to canonicalize the assigned variable before any arithmetic operations are performed on that variable.
	
	gmp_fprintf (stderr, "\tas a decimal rational number = %Qd\n", angle); // 
	fprintf( stderr	, "\tas a formated binary string = 0%s\n", s);
	
	
	// ---------------------------------------------------
	
	mpfr_init2(cre, 53);
	mpfr_init2(cim, 53);
	
	
	return 0;
}


int compute_ray(mpq_t angle){



	
	
	ray = mandelbrot_external_ray_in_new(angle);
	if (ray ==NULL ){ fprintf(stderr, " ray error \n"); return 1;}
	
	for (int i = 0; i < depth * 4; ++i) { // FIXME 4 = implementation's sharpness
		//fprintf( stderr	, "i = %d\n", i);
		mandelbrot_external_ray_in_step(ray); //fprintf(stderr, " ray step ok \n");
		mandelbrot_external_ray_in_get(ray, cre, cim); //fprintf(stderr, " ray get ok \n");
		mpfr_out_str(stdout, 10, 0, cre, GMP_RNDN);
		
		putchar(' ');
		mpfr_out_str(stdout, 10, 0, cim, GMP_RNDN);
		putchar('\n');
		}
	
	
	return 0;



}




int end(void){

	PrintInfo();
	fprintf(stderr, " allways free memory (deallocate )  to avoid memory leaks \n");	// wikipedia C_dynamic_memory_allocation
	mpq_clear (angle);
	mpfr_clear(cre);
	mpfr_clear(cim);
	mandelbrot_external_ray_in_delete(ray);
	return 0;
}

int main(void){
	
	setup();

	compute_ray(angle);
	end();

	return 0;
}

Python

Ray in procedure

r"""
Mandelbrot and Julia sets (Cython helper)

This is the helper file providing functionality for mandel_julia.py.
https://git.sagemath.org/sage.git/tree/src/sage/dynamics/complex_dynamics/mandel_julia_helper.pyx?id=bf9df0d7ff4f272b19293fd0d04ef3a649d05863

AUTHORS:

- Ben Barros

"""

#*****************************************************************************
#       Copyright (C) 2017 BEN BARROS <bbarros@slu.edu>
#
# This program is free software: you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation, either version 2 of the License, or
# (at your option) any later version.
#                  http://www.gnu.org/licenses/
#*****************************************************************************

from __future__ import absolute_import, division
from sage.plot.colors import Color
from sage.repl.image import Image
from copy import copy
from cysignals.signals cimport sig_check
from sage.rings.complex_field import ComplexField
from sage.functions.log import exp, log
from sage.symbolic.constants import pi


def external_ray(theta, **kwds):
    r"""
    Draws the external ray(s) of a given angle (or list of angles)
    by connecting a finite number of points that were approximated using
    Newton's method. The algorithm used is described in a paper by
    Tomoki Kawahira.
    https://git.sagemath.org/sage.git/tree/src/sage/dynamics/complex_dynamics/mandel_julia.py?id=bf9df0d7ff4f272b19293fd0d04ef3a649d05863
    REFERENCE:

    [Kaw2009]_

    INPUT:

    - ``theta`` -- double or list of doubles, angles between 0 and 1 inclusive.

    kwds:

    - ``image`` -- 24-bit RGB image (optional - default: None) user specified image of Mandelbrot set.

    - ``D`` -- long (optional - default: ``25``) depth of the approximation. As ``D`` increases, the external ray gets closer to the boundary of the Mandelbrot set. If the ray doesn't reach the boundary of the Mandelbrot set, increase ``D``.

    - ``S`` -- long (optional - default: ``10``) sharpness of the approximation. Adjusts the number of points used to approximate the external ray (number of points is equal to ``S*D``). If ray looks jagged, increase ``S``.

    - ``R`` -- long (optional - default: ``100``) radial parameter. If ``R`` is large, the external ray reaches sufficiently close to infinity. If ``R`` is too small, Newton's method may not converge to the correct ray.

    - ``prec`` -- long (optional - default: ``300``) specifies the bits of precision used by the Complex Field when using Newton's method to compute points on the external ray.

    - ``ray_color`` -- RGB color (optional - default: ``[255, 255, 255]``) color of the external ray(s).

    OUTPUT:

    24-bit RGB image of external ray(s) on the Mandelbrot set.

    EXAMPLES::

        sage: external_ray(1/3)
        500x500px 24-bit RGB image

    ::

        sage: external_ray(0.6, ray_color=[255, 0, 0])
        500x500px 24-bit RGB image

    ::

        sage: external_ray([0, 0.2, 0.4, 0.7]) # long time
        500x500px 24-bit RGB image

    ::

        sage: external_ray([i/5 for i in range(1,5)]) # long time
        500x500px 24-bit RGB image

    WARNING:

    If you are passing in an image, make sure you specify
    which parameters to use when drawing the external ray.
    For example, the following is incorrect::

        sage: M = mandelbrot_plot(x_center=0) # not tested
        sage: external_ray(5/7, image=M) # not tested
        500x500px 24-bit RGB image

    To get the correct external ray, we adjust our parameters::

        sage: M = mandelbrot_plot(x_center=0) # not tested
        sage: external_ray(5/7, x_center=0, image=M) # not tested
        500x500px 24-bit RGB image

    TODO:

    The ``copy()`` function for bitmap images needs to be implemented in Sage.
    """

    x_0 = kwds.get("x_center", -1)
    y_0 = kwds.get("y_center", 0)
    plot_width = kwds.get("image_width", 4)
    pixel_width = kwds.get("pixel_count", 500)
    depth = kwds.get("D", 25)
    sharpness = kwds.get("S", 10)
    radial_parameter = kwds.get("R", 100)
    precision = kwds.get("prec", 300)
    precision = max(precision, -log(pixel_width * 0.001, 2).round() + 10)
    ray_color = kwds.get("ray_color", [255]*3)
    image = kwds.get("image", None)
    if image is None:
        image = mandelbrot_plot(**kwds)

    # Make a copy of the bitmap image.
    # M = copy(image)
    old_pixel = image.pixels()
    M = Image('RGB', (pixel_width, pixel_width))
    pixel = M.pixels()
    for i in range(pixel_width):
        for j in range(pixel_width):
            pixel[i,j] = old_pixel[i,j]

    # Make sure that theta is a list so loop below works
    if type(theta) != list:
        theta = [theta]

    # Check if theta is in the invterval [0,1]
    for angle in theta:
        if angle < 0 or angle > 1:
            raise \
            ValueError("values for theta must be in the closed interval [0,1].")

    # Loop through each value for theta in list and plot the external ray.
    for angle in theta:
        E = fast_external_ray(angle, D=depth, S=sharpness, R=radial_parameter,
         prec=precision, image_width=plot_width, pixel_count=pixel_width)

        # Convert points to pixel coordinates.
        pixel_list = convert_to_pixels(E, x_0, y_0, plot_width, pixel_width)

        # Find the pixels between points in pixel_list.
        extra_points = []
        for i in range(len(pixel_list) - 1):
            if min(pixel_list[i+1]) >= 0 and max(pixel_list[i+1]) < pixel_width:
                for j in get_line(pixel_list[i], pixel_list[i+1]):
                    extra_points.append(j)

        # Add these points to pixel_list to fill in gaps in the ray.
        pixel_list += extra_points

        # Remove duplicates from list.
        pixel_list = list(set(pixel_list))

        # Check if point is in window and if it is, plot it on the image to
        # create an external ray.
        for k in pixel_list:
            if max(k) < pixel_width and min(k) >= 0:
                pixel[int(k[0]), int(k[1])] = tuple(ray_color)
    return M




cpdef fast_external_ray(double theta, long D=30, long S=10, long R=100,
 long pixel_count=500, double image_width=4, long prec=300):
    r"""
    Returns a list of points that approximate the external ray for a given angle.

    INPUT:

    - ``theta`` -- double, angle between 0 and 1 inclusive.

    - ``D`` -- long (optional - default: ``25``) depth of the approximation. As ``D`` increases, the external ray gets closer to the boundary of the Mandelbrot set.

    - ``S`` -- long (optional - default: ``10``) sharpness of the approximation. Adjusts the number of points used to approximate the external ray (number of points is equal to ``S*D``).

    - ``R`` -- long (optional - default: ``100``) radial parameter. If ``R`` is sufficiently large, the external ray reaches enough close to infinity.

    - ``pixel_count`` -- long (optional - default: ``500``) side length of image in number of pixels.

    - ``image_width`` -- double (optional - default: ``4``) width of the image in the complex plane.

    - ``prec`` -- long (optional - default: ``300``) specifies the bits of precision used by the Complex Field when using Newton's method to compute points on the external ray.

    OUTPUT:

    List of tuples of Real Interval Field Elements

    EXAMPLES::

        sage: from sage.dynamics.complex_dynamics.mandel_julia_helper import fast_external_ray
        sage: fast_external_ray(0,S=1,D=1)
        [(100.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000,
          0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000),
         (9.51254777713729174697578576623132297117784691109499464854806785133621315075854778426714908,
          0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000)]


    ::

        sage: from sage.dynamics.complex_dynamics.mandel_julia_helper import fast_external_ray
        sage: fast_external_ray(1/3,S=1,D=1)
        [(-49.9999999999999786837179271969944238662719726562500000000000000000000000000000000000000000,
          86.6025403784438765342201804742217063903808593750000000000000000000000000000000000000000000),
         (-5.50628047023173006234970878097113901879832542655926629309001652388544528575532346900138516,
          8.64947510053972513843999918917106032664030380426885745306040284140385975750462108180377187)]

    ::

        sage: from sage.dynamics.complex_dynamics.mandel_julia_helper import fast_external_ray
        sage: fast_external_ray(0.75234,S=1,D=1)
        [(1.47021239172637052661229972727596759796142578125000000000000000000000000000000000000000000,
          -99.9891917935294287644865107722580432891845703125000000000000000000000000000000000000000000),
         (-0.352790406744857508500937144524776555433184352559852962308757189778284058275081335121601384,
          -9.98646630765023514178761177926164047797465369576787921409326037870837930920646860774032363)]
    """

    cdef:
        CF = ComplexField(prec)
        PI = CF.pi()
        I = CF.gen()
        c_0, r_m, t_m, temp_c, C_k, D_k, old_c, x, y, dist
        int k, j, t
        double difference, m
        double error = pixel_count * 0.0001

        double pixel_width = image_width / pixel_count

        # initialize list with c_0
        c_list = [CF(R*exp(2*PI*I*theta))]

    # Loop through each subinterval and approximate point on external ray.
    for k in range(1,D+1):
        for j in range(1,S+1):
            m = (k-1)*S + j
            r_m = CF(R**(2**(-m/S)))
            t_m = CF(r_m**(2**k) * exp(2*PI*I*theta * 2**k))
            temp_c = c_list[-1]
            difference = error

            # Repeat Newton's method until points are close together.
            while error <= difference:
                sig_check()
                old_c = temp_c
                # Recursive formula for iterates of q(z) = z^2 + c
                C_k, D_k = CF(old_c), CF(1)
                for t in range(k):
                    C_k, D_k = C_k**2 + old_c, CF(2)*D_k*C_k + CF(1)
                temp_c = old_c - (C_k - t_m) / D_k   # Newton map
                difference = abs(old_c) - abs(temp_c)

            dist = (2*C_k.abs()*(C_k.abs()).log()) / D_k.abs()
            if dist < pixel_width:
                break
            c_list.append(CF(temp_c))
        if dist < pixel_width:
            break

    # Convert Complex Field elements into tuples.
    for k in range(len(c_list)):
        x,y = c_list[k].real(), c_list[k].imag()
        c_list[k] = (x, y)

    return c_list

Test and precision

angle $\theta$ in turns	landing point $c_{\infty }$	precision
0	1/4
1/2	-2
1/3	-3/4
1/4	-0.228155493653962 +1.115142508039937i
1/5	-0.154724526314600 +1.031047184160779i
1/6	i
1/10	0.384063957 +0.666805123i

See

• here
• Y-C Chen, T Kawahira, H-L Li, and J-M Yuan FAMILY OF INVARIANT CANTOR SETS AS ORBITS OF DIFFERENTIAL EQUATIONS. II: JULIA SETS (8475K, PDF) Dec 6, 09

The Wolf Jung test : The external parameter rays for angles (in turns)

• 1/7 (period 3)
• 321685687669320/2251799813685247 (period 51)
• 321685687669322/2251799813685247 ( period 51 )

Angles differ by about $10^{-15}$, but the landing points of the corresponding parameter rays are about 0.035 apart.

References

• Wolf Jung old page in web archive
• How to handle branch cuts in Böttcher functions
• Wolfram Research (2014), MandelbrotSetBoettcher, Wolfram Language function, https://reference.wolfram.com/language/ref/MandelbrotSetBoettcher.html.
• algorithms for computing angles in the mandelbrot set - Douady