Fractals/Mathematics/periodic points of complex quadratic map
Periodic points of complex quadratic map
[edit | edit source]This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the variable and the parameters are complex numbers. A periodic point of a map is a value of the variable that occurs repeatedly after intervals of a fixed length.
These periodic points play a role in the theories of Fatou and Julia sets.
Definitions
[edit | edit source]Let
be the complex quadric mapping, where and are complex numbers.
Notationally, is the -fold composition of with itself (not to be confused with the th derivative of )—that is, the value after the k-th iteration of the function Thus
Periodic points of a complex quadratic mapping of period are points of the dynamical plane such that
where is the smallest positive integer for which the equation holds at that z.
We can introduce a new function:
so periodic points are zeros of function : points z satisfying
which is a polynomial of degree
Number of periodic points
[edit | edit source]The degree of the polynomial describing periodic points is so it has exactly complex roots (= periodic points), counted with multiplicity.
Stability of periodic points (orbit) - multiplier
[edit | edit source]
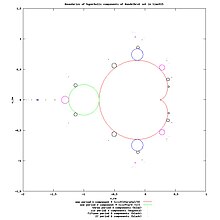

The multiplier (or eigenvalue, derivative) of a rational map iterated times at cyclic point is defined as:
where is the first derivative of with respect to at .
Because the multiplier is the same at all periodic points on a given orbit, it is called a multiplier of the periodic orbit.
The multiplier is:
- a complex number;
- invariant under conjugation of any rational map at its fixed point;[1]
- used to check stability of periodic (also fixed) points with stability index
A periodic point is[2]
- attracting when
- super-attracting when
- attracting but not super-attracting when
- indifferent when
- rationally indifferent or parabolic if is a root of unity;
- irrationally indifferent if but multiplier is not a root of unity;
- repelling when
Periodic points
- that are attracting are always in the Fatou set;
- that are repelling are in the Julia set;
- that are indifferent fixed points may be in one or the other.[3] A parabolic periodic point is in the Julia set.
Finding periodic points
[edit | edit source]solve these equations using numerical methods for solving polynomials - and even something simple such as Newton's method is going to converge a lot faster than finding the cycles just by iterating a single point (as is how bifurcations diagrams are usually made) under fc itself. Milo Brandt[4]
Methods:
- simple iterating and checking convergence
- numerical methods
- symbolic computations, algebraic
- numerical methods for finding roots of polynomial equations
Period-1 points (fixed points)
[edit | edit source]Finite fixed points
[edit | edit source]Let us begin by finding all finite points left unchanged by one application of . These are the points that satisfy . That is, we wish to solve
which can be rewritten as
Since this is an ordinary quadratic equation in one unknown, we can apply the standard quadratic solution formula:
- and
So for we have two finite fixed points and .
Since
- and where
we have .
Thus fixed points are symmetrical about .
Complex dynamics
[edit | edit source]

Here different notation is commonly used:[5]
- with multiplier
and
- with multiplier
Again we have
Distance between fixed points:
is delta
where
- so
- for distance is equal to zero: =the points coincide ( parabolic case)
- for distance is equal to 1: = the superattracting case ( alfa is a center and beta in on the unit circle)
Since the derivative with respect to z is
we have
This implies that can have at most one attractive fixed point.
These points are distinguished by the facts that:
- is:
- the landing point of the external ray for angle=0 for
- the most repelling fixed point of the Julia set
- the one on the right (whenever fixed point are not symmetrical around the real axis), it is the extreme right point for connected Julia sets (except for cauliflower).[6]
- is:
- the landing point of several rays
- attracting when is in the main cardioid of the Mandelbrot set, in which case it is in the interior of a filled-in Julia set, and therefore belongs to the Fatou set (strictly to the basin of attraction of finite fixed point)
- parabolic at the root point of the limb of the Mandelbrot set
- repelling for other values of
Special cases
An important case of the quadratic mapping is . In this case, we get and . In this case, 0 is a superattractive fixed point, and 1 belongs to the Julia set.
Only one fixed point
We have exactly when This equation has one solution, in which case . In fact is the largest positive, purely real value for which a finite attractor exists.
Infinite fixed point
[edit | edit source]We can extend the complex plane to the Riemann sphere (extended complex plane) by adding infinity:
and extend such that
Then infinity is:
- superattracting
- a fixed point of :[7]
Period-2 cycles
[edit | edit source]

Period-2 cycles are two distinct points and such that and , and hence
for :
Equating this to z, we obtain
This equation is a polynomial of degree 4, and so has four (possibly non-distinct) solutions. However, we already know two of the solutions. They are and , computed above, since if these points are left unchanged by one application of , then clearly they will be unchanged by more than one application of .
Our 4th-order polynomial can therefore be factored in 2 ways:
First method of factorization
[edit | edit source]This expands directly as (note the alternating signs), where
We already have two solutions, and only need the other two. Hence the problem is equivalent to solving a quadratic polynomial. In particular, note that
and
Adding these to the above, we get and . Matching these against the coefficients from expanding , we get
- and
From this, we easily get
- and .
From here, we construct a quadratic equation with and apply the standard solution formula to get
- and
Closer examination shows that:
- and
meaning these two points are the two points on a single period-2 cycle.
Second method of factorization
[edit | edit source]We can factor the quartic by using polynomial long division to divide out the factors and which account for the two fixed points and (whose values were given earlier and which still remain at the fixed point after two iterations):
The roots of the first factor are the two fixed points. They are repelling outside the main cardioid.
The second factor has the two roots
These two roots, which are the same as those found by the first method, form the period-2 orbit.[8]
Special cases
[edit | edit source]Again, let us look at . Then
- and
both of which are complex numbers. We have . Thus, both these points are "hiding" in the Julia set. Another special case is , which gives and . This gives the well-known superattractive cycle found in the largest period-2 lobe of the quadratic Mandelbrot set.
Cycles for period greater than 2
[edit | edit source]
The degree of the equation is 2n; thus for example, to find the points on a 3-cycle we would need to solve an equation of degree 8. After factoring out the factors giving the two fixed points, we would have a sixth degree equation.
There is no general solution in radicals to polynomial equations of degree five or higher, so the points on a cycle of period greater than 2 must in general be computed using numerical methods. However, in the specific case of period 4 the cyclical points have lengthy expressions in radicals.[9]
In the case c = –2, trigonometric solutions exist for the periodic points of all periods. The case is equivalent to the logistic map case r = 4: Here the equivalence is given by One of the k-cycles of the logistic variable x (all of which cycles are repelling) is
general numerical methods
[edit | edit source]
What I do to create an periodic components of Mandelbrot set, for :
- start iteration from , with
- for each in order
- calculate
- if
- set
- use Newton's method to solve with initial guess (this may fail to converge, in which case continue with the next ), the steps are
- calculate the derivative of the cycle
- if , then the cycle is attractive and is within a hyperbolic component of period , stop (success).
Where:
- may used as "interior coordinates" within the hyperbolic component.
- and can be used for interior distance estimation.
The point of using Newton's method is to accelerate the computation of , a point in the limit cycle attractor. Computing just by iterating could take many 1000s of iterations, especially when is close to .
I have no complete proof of correctness (but this doesn't mean I think it is incorrect; the images seem plausible). It relies on the "atom domains" surrounding each hyperbolic component of a given period.
It also relies on the cycle reached by Newton's method being the same cycle as the limit cycle approached by iteration: this is true for the quadratic Mandelbrot set because there is only one finite critical point, ( is a fixed point) and each attracting or parabolic cycle has a critical point in its immediate basin (see <https://math.stackexchange.com/a/3952801>), which means there can be at most one attracting or parabolic cycle.
For an implementation in C99 you can see my blog post at <https://mathr.co.uk/blog/2014-11-02_practical_interior_distance_rendering.html>
Speed up
[edit | edit source]Cardioid / bulb checking:
int GivePeriod(complex double c){
if (cabs2(c)>4.0) {return 0;} // exterior : out of first lemniscte
if (cabs2(1.0 - csqrt(1.0-4.0*c))<=1.0 ) {return 1;} // main cardioid
if (cabs2(4.0*c + 4)<=1.0){return 2;} // period 2 component
int period = GivePeriodByIteration(c);
if ( period < 0) // last chance
{
iUnknownPeriod +=1;
//period = m_d_box_period_do(c, 0.5, iterMax_LastIteration); // not working good
}
// period > 0 means is periodic
// period = 0 means is not periodic = exterior = escaping to infinity
// period < 0 means period not found, maybe increase global variable iterMax_Period ( see local_setup)
return period;
}
Further reading
[edit | edit source]- Geometrical properties of polynomial roots
- Alan F. Beardon, Iteration of Rational Functions, Springer 1991, ISBN 0-387-95151-2
- Michael F. Barnsley (Author), Stephen G. Demko (Editor), Chaotic Dynamics and Fractals (Notes and Reports in Mathematics in Science and Engineering Series) Academic Pr (April 1986), ISBN 0-12-079060-2
- Wolf Jung : Homeomorphisms on Edges of the Mandelbrot Set. Ph.D. thesis of 2002
- The permutations of periodic points in quadratic polynominials by J Leahy
External links
[edit | edit source]- Algebraic solution of Mandelbrot orbital boundaries by Donald D. Cross
- Brown Method by Robert P. Munafo
- arXiv:hep-th/0501235v2 V.Dolotin, A.Morozov: Algebraic Geometry of Discrete Dynamics. The case of one variable.
References
[edit | edit source]- ↑ Alan F. Beardon, Iteration of Rational Functions, Springer 1991, ISBN 0-387-95151-2, p. 41
- ↑ Alan F. Beardon, Iteration of Rational Functions, Springer 1991, ISBN 0-387-95151-2, page 99
- ↑ Some Julia sets by Michael Becker
- ↑ math.stackexchange question: equations-for-mandelbrot-bifurcation-diagram?
- ↑ On the regular leaf space of the cauliflower by Tomoki Kawahira Source: Kodai Math. J. Volume 26, Number 2 (2003), 167-178. Template:Webarchive
- ↑ Periodic attractor by Evgeny Demidov Template:Webarchive
- ↑ R L Devaney, L Keen (Editor): Chaos and Fractals: The Mathematics Behind the Computer Graphics. Publisher: Amer Mathematical Society July 1989, ISBN 0-8218-0137-6 , ISBN 978-0-8218-0137-6
- ↑ Period 2 orbit by Evgeny Demidov Template:Webarchive
- ↑ Gvozden Rukavina : Quadratic recurrence equations - exact explicit solution of period four fixed points functions in bifurcation diagram



































































































































