Basic Physics of Digital Radiography/The Applications

A selection of clinical applications of Digital Radiography are described in this chapter. General Radiography, being one of the mainstays of Diagnostic Radiography, has changed from a film-based imaging process to one based on digital technologies. The impact of these changes in terms of radiation dose and image quality are discussed in this chapter. Specialised applications such as Mammography, Digital Subtraction Angiography, C-Arm Computed Tomography, Multi-Detector CT, Dual-Energy Radiography and Image Fusion are also considered.
General Radiography
[edit | edit source]Digital image receptors have been increasingly applied in general radiography since the turn of the century. Early studies indicated its superior image quality relative to film/screen technology in skeletal radiography[1][2]. On this basis, refinements of exposure technique have also occurred[3][4][5][6]. Furthermore, dose comparisons with traditional radiography and various forms of Computed Radiography (CR) with direct and indirect Digital Radiography (DR) have been made[7][8][9]. In addition, the performance of digital image receptors for fluoroscopic applications has also been investigated[10].
Results of these investigations have indicated significant advantages in favour of the digital technology. In general, the change in image receptors has been technically similar to the transition from film-based to digital cameras in photography. However, work practice changes and capital cost are major considerations with the implementation of digital radiography[11].
Experience to the year 2010 has indicated that from a physics perspective[12][13]:
- Standard CR plates provide no dose reduction relative to traditional 400-speed film/screen systems,
- Dual-side read-out CR has a DQE about 40–50% higher than single-side read-out CR,
- Stuctured phosphor CR has a DQE about 50% higher than dual-side read-out CR and approaches that of indirect DR,
- Indirect DR receptors with structured phosphors have a DQE about twice that of direct DR receptors at spatial frequencies below 4 LP/mm,
- Doses with indirect, structured phosphor DR are 30–50% lower than 400-speed film/screen systems, and
- Dose savings are limited for highly attenuating regions of the body (e.g. retro-cardiac and infra-diaphragmatic areas of chest radiographs), but can exceed 50% in regions of high X-ray transparency (e.g. the lung fields).
From a practical perspective, convenience has been enhanced in the clinical application of these devices by the incorporation of Wi-Fi connectivity between the image receptor and the digital image processor. CR imaging cassettes, including read-out device, and DR cassettes of similar size to the traditional film/screen cassettes have also been developed. These can therefore be used without much change in the design of patient tables, upright Bucky stands and other radiographic apparatus.
The application of DR technologies has also led the development of new imaging techniques, such as Digital Tomosynthesis and Temporal Subtraction, and to new forms of digital image processing, e.g. rib suppression in chest radiography[14] and Computer-Assisted Diagnosis (CAD)[15]. These topics however are beyond the scope of our considerations here.
Mammography
[edit | edit source]Mammography is a form of soft tissue imaging and the instrumentation used is designed specifically for imaging the female breast. Low X-ray energies are therefore required to exploit the Photoelectric Effect and thereby enhance the discrimination between different types of tissues. In addition, fine details such as microcalcifications also need to be resolved by the imaging system. Small focal spot XRTs and high resolution image receptors are therefore required. These specific requirements are considered in more detail below.
Mammography X-Ray Tubes
[edit | edit source]- An X-ray energy of ~20 keV is needed to generate adequate subject contrast between different tissues. Such an energy provides discrimination between infiltrating duct carcinomas and fat, for example, although with little differentiation between fat and fibrous tissue[16].

- Molybdenum (Mo) can be used instead of tungsten as the anode material in the X-ray tube (XRT). The Mo energy spectrum consists of K-Characteristic lines between 17 and 19 keV and a Bremsstrahlung continuum - see Figure 7.22. The Bremsstrahlung can be attenuated using an added Mo filter which preferentially eliminates the low energy radiation, that would otherwise be completely absorbed by the tissues and contribute little to image formation, as well as higher energy X-rays which would otherwise degrade subject contrast. This is an example of the application of K-edge filtration.
- Rhodium (Rh) can also be used for both the anode and the filter materials. Rh has a K-edge at 23.2 keV, which is a little above that of Mo, and this can offer advantages for imaging the thicker, denser breast at a lower absorbed dose than with the Mo anodes. This results because of the superior penetration of the Rh K-shell characteristic X-rays. Other anode/filter combinations, such as Mo/Rh, W/Ag and W/Rh have also been used.
- Most X-ray tubes used for contact mammography have small focal spots (e.g. 0.3 mm) which are less than half the size used in general radiography. Such small focal spots are needed to image fine detail such as microcalcifications, that may be no larger than 100 μm. The resultant heating of the XRT anode can limit tube currents to a maximum of no more than ~100 mA at 25 kV so that long exposure times up to 3 seconds or more are needed to compensate. Patient movement therefore needs to be suppressed during the exposure.
- Mammography XRTs are generally constructed with a metal envelope, instead of the usual glass, with a thin beryllium (Be) exit port. This design has the advantage of suppressing extra-focal radiation. In addition, the tube can be constructed so that the anode-cathode axis is offset to achieve the small focal spot size - see Figure 7.23.
- Furthermore, it has been found that the focal spot should be located on a line, perpendicular to the image receptor, which contains the chest wall margin. Equally importantly, the collimator should also be adjusted to ensure that the X-ray beam intercepts the image receptor on that margin.

Mammography Image Receptors
[edit | edit source]- An ideal imaging system for mammography would require a limiting spatial resolution of ~20 LP/mm or more and a dynamic range of at least 5,000:1, achieved with minimal radiation dose to the patient. A matrix size of at least 9,600x7,200 pixels, each with a minimum of 12 bits depth, would be needed to achieve the required spatial resolution within a typical field of view of 18x24 cm. The computer storage required for one image would therefore be 132 Mbytes. Even at a limiting resolution of 10 LP/mm, 33 Mbytes of storage would still be needed for a single digital image.
- The major problem with applying CR technology to mammography is its spatial resolution, which is limited to less than ~5 LP/mm, with the sampling rate of 10 pixels/mm as generally used. The anticipated loss of resolution may not be a serious problem, however, because of the superior contrast and dynamic range available for post-acquisition digital image processing. Reducing the diameter of the stimulating laser beam, use of a thinner phosphor layer and dual-sided read-out CR plates[17] are three approaches which can be used to address this issue.
- Both direct and indirect DR receptors can be used for Digital Mammography. Here, the manufacturing technology limits pixel size to about 70-100 μm for image sizes up to 3,328x4,096 pixels of area up to 24x29 cm. Once again, it is assumed that the lack of spatial resolution is compensated by the broad dynamic range of the image receptor as well as the spatial frequency and contrast enhancement capabilities of digital image processing.
- Another technique for obtaining a digital image involves coupling a conventional phosphor screen to a Charge Coupled Device (CCD) using lenses or fibre optic coupling. The CCD matrix can be just 1,024x1,024 pixels in small field applications and systems have demonstrated limiting spatial resolutions of ~10 LP/mm. Larger fields of view can be achieved using an array of CCDs - see Figure 7.24, panel (a). When individual pixels are of size 40 μm and a detector area of 18x24 cm, an image matrix of 4,800x6,400 pixels results, which can provide a spatial resolution of 12.5 LP/mm. Broader area receptors have also found application in General Radiography, and digital implementation of Multiple Beam Equalization Radiography (AMBER) has been investigated[18].

Fig. 7.24: (a) A large phosphor screen coupled to several CCDs using fibre optic tapers; (b) A scanning-slot system where a narrow phosphor screen is coupled by the fibre optics to a few CCDs and the XRT/detector is scanned across the anatomy.
- Another alternative is to use a slot scanning arrangement - see Figure 7.24, panel (b). Here, X-rays transmitted through the compressed breast produce light in a strip of CsI:Tl phosphor and this light is collected by the fibre optics and conveyed to the CCD arrays. Some features of this design are:
- the X-ray beam is collimated to a fan of narrow width (e.g. 22 x 1 cm), giving high level of scatter rejection,
- the phosphor is coupled to a number of discrete CCD arrays abutted together to form a linear array. Each CCD array has 2,048x400 pixels of sufficiently small size that the system achieves a spatial resolution of 10 LP/mm or greater,
- the image is acquired line by line by scanning the fan-shaped X-ray beam across the breast at a constant speed - see Figure 7.25. This form of image acquisition is analogous to the Scanned Projection Radiography image, also called Scout View, used in Computed Tomography (CT) scanning,
- Image acquisition time is 5 seconds, and
- Since the X-ray field-of-view and phosphor detector are relatively small, scatter does not represent a serious problem and grids do not need to be used - which represents a potential dose saving for patients.

- One of the disadvantages of the scanning slot approach is the necessity for long exposure times which increases the load on the X-ray tube. This can be addressed using a tungsten anode XRT, which has a substantially greater efficiency for X-ray production and heat dissipation than a tube with a molybdenum anode. The tube can operated between 20 and 45 kV with a choice of Al, Mo or Rh filters. This may seem counterproductive given the earlier discussion on the importance of using low kV in order to achieve high subject contrast. However, the detector has a dynamic range of 5,000:1 so that, while subject contrast is reduced, high image contrast can nevertheless be achieved.
- Scanning systems have also been developed based on photon counting detectors, e.g. crystalline silicon X-ray detectors and multichannel gaseous ionisation chambers. These have the advantage that they detect each X-ray photon absorption event in the detector, instead of integrating the image signal generated by multiple photons as occurs with conventional image receptors. Image noise can therefore be suppressed using thresholding techniques.
- The performance of five imaging systems for Digital Mammography is compared in Lazzari et al. (2007)[19]. A higher DQE for direct over indirect DR image receptors was found, and both were superior to a scanning-slot system. Further, the application of digital tomosynthesis to mammography[20], called Digital Breast Tomosynthesis (DBT), has been investigated[21].
- The historical development of mammography is reviewed in Sprawls (2019)[22].
Mammography AEC
[edit | edit source]- Unlike the AEC in conventional radiography, the controlling detector cannot be placed in front of a CR imaging cassette because it would attenuate the X-ray beam too severely and cast its own X-ray shadow. The shadow is significant especially at the low X-ray energies used in mammography. However, when it is placed behind the cassette, the amount of X-ray flux reaching the controlling detector is strongly influenced by absorption in the image receptor, which in itself is strongly dependent on the energy of the X-ray photons emerging from the patient. The net result is that conventional AEC devices compensate very poorly for changes in breast type, thickness and kilo-voltage. These problems can be overcome,however, using microprocessor-controlled HV generator switching. The AEC detector measures the instantaneous dose-rate and, based on the selected kV and/or the measured breast thickness, terminates the exposure at the appropriate time using a look-up table (LUT). There can be a separate LUT set up for each operational mode, e.g. contact mammography with a grid, contact without a grid and magnified imaging.
- The function of an AEC can be expanded using the Auto-kV mode of operation. The control system quickly decides, within ~10-30 ms of exposure initiation, whether the selected kV is going to allow the desired image quality to be achieved in a sufficiently short time. If not, the kV can be increased appropriately to ensure that the exposure time limit, dictated by the tube loading, is not exceeded.
- Direct radiography (DR) systems can use the image receptor itself as the AEC sensor[23].
Mammography Scatter Reduction
[edit | edit source]- Compression of the breast tissues is critical for:
- reducing scattered radiation that would otherwise reduce subject contrast,
- improving contrast by decreasing the amount of beam hardening that occurs as the X-ray beam passes through the tissues,
- immobilising the breast,
- locating breast structure closer to the imaging plane,
- producing a more uniform breast thickness, and
- reducing absorbed dose through the use of reduced exposure times.
- Compression pads can be made from a thin plate of polycarbonate or perspex. Their design is such that creeping of breast tissue up the chest wall is prevented when the breast is being compressed.
- In addition, grids are used to further reduce scattered radiation and improve subject contrast. They are typically moving grids made with a carbon fibre interspace, although other designs are also in use, e.g. honeycomb grids with copper as the attenuator and air as the interspace material. Bucky Factors are typically 2-2.5 for grid ratios of 4:1 or 5:1.
- Adequate subject contrast is generally achieved with kilo-voltages less than 28 kV, and even lower (e.g. 23 kV) for thinner breast thicknesses.
Magnification Mammography
[edit | edit source]
- Magnification mammography with m = 1.5-2.0 is widely used in follow-up studies where lesion localization techniques might be necessary. There are several technical advantages associated with magnification radiography, which include:
- improved spatial resolution of the recording system,
- reduction of image noise arising from the structural components of the image receptor, and
- reduction of scatter because of the air gap (e.g. 15-30 cm), particularly in coned down magnification studies.
- Note that these advantages are achieved at the expense of increased radiation dose to the part of the breast in the primary beam because of a consequent requirement to position the breast closer to the X-ray tube in many clinical systems - see Figure 7.26, for example.
- In addition, a focal spot as small as 0.1 mm is typically used for magnification mammography. Problems with long exposure times are significant in situations where the maximum tube current is only 15-25 mA. A compromise between patient movement and subject contrast can be reached by increasing the kilo-voltage to 30-32 kV so as to keep the exposure time within reasonable bounds. However, it should be appreciated that magnification imaging is a higher dose technique which is caused by the proximity of the breast to the focal spot, so that an increase in the skin dose by anything up to a factor of four results. Although this increase is partially offset by the fact that only a region of the breast is generally irradiated and a grid is not necessary for such views, the net result is an increase in absorbed dose by a factor of about two.
Stereotactic imaging can be used to assist core biopsy sampling using, for example, 14-gauge needles. Although attachments can be made to conventional mammography equipment for these procedures, superior ergonomics is provided by prone systems with the breast to be biopsied placed in a pendant position through a hole in the patient couch. The XRT, compression pad, imaging receptor and biopsy gun are all mounted below the table whose height can be adjusted to allow sufficient space for positioning the needle. The biopsy gun is typically mounted on a Vernier driven table that allows accurate positioning of the needle during the biopsy procedure. Images of the localized region containing the suspicious lesion in the compressed breast are generally taken with the XRT at two different locations, usually ±15° to a line perpendicular to the image plane, so to provide co-ordinate information for the computer-controlled advance of the biopsy needle.
Finally, it should be noted that mammography screening was conducted annually in a cohort of 100,000 women from ages 40 to 55 years and biennially until 74 years at a dose of 3.7 mGy per breast examination[24]. It was predicted that these exposures would ultimately induce 86 breast cancers, 11 fatal, and that 10,670 woman-years would be saved because of early detection. The risk of radiation-induced breast cancer associated with routine mammographic screening of women over 40 is therefore considered to be extremely low, especially when compared with the anticipated benefits of screening, and, as a consequence, radiation risk should not deter women from mammographic screening.
Digital Subtraction Angiography
[edit | edit source]Digital Subtraction Angiography (DSA), as the name implies, involves an image subtraction technique - see Figure 7.1. As will be seen below, the technique involves more than simply applying a subtraction process in the digital image processor. In addition, it will be seen that the type of technology utilised, while based on the design of fluoroscopy systems, needs to incorporate a number of modifications unique to DSA. Before addressing the technology however, some basic physics needs to be introduced which will aid in putting the subsequent technology discussion into context.

Basic DSA Physics
[edit | edit source]- The process of subtraction angiography, as illustrated simplistically in Figure 7.2, involves the subtraction of a post-opacification image (commonly called the Live image) from a pre-opacification image of the same region (commonly called the Mask image). When it is assumed that monoenergetic X-rays irradiate the patient and that no scattered radiation is generated, the radiation intensity, I2, for an appropriate point of the live image is related to the intensity, I1, for the same point of the mask image, by:

- where μc, ρc and tc are the mass attenuation coefficient, concentration and thickness, respectively, of the contrast medium. Thus, when I2 is subtracted directly from I1, the subtracted image is given by:
- Thus,
- and, hence
- This equation indicates that the subtraction signal, D, contains information from the mask image I1, as well as from the live image. As a result, the density of opacified vessels in the subtraction image will contain artifacts which are dependent on the anatomical details which underlie and overlap the blood vessels within the patient. These artifacts result because of the exponential nature of radiation attenuation in matter. They may be reduced ideally by computing the natural logarithm of the transmitted intensities prior to subtraction. When this is done the subtraction image is now dependent on the contrast medium only - with no artifacts from surrounding anatomy, as follows:
- so that:
- and therefore,
- Many DSA systems utilise the above reasoning to logarithmically transform both the mask and the live images prior to subtraction. A second theoretical advantage of this logarithmic subtraction process is the generation of images which are not influenced by spatial non-uniformities of the imaging device. X-ray image intensifiers, for example, display significant spatial non-uniformities.
- A third theoretical advantage of logarithmic subtraction is the generation of images in which the image density is directly proportional to the projected thickness of the contrast medium, ρctc. This feature has given rise to the use of densitometric analysis of images so as to derive clinically-useful indices of function, e.g. percent stenosis and left ventricular ejection fraction. However, it is important to note that the above reasoning is based on a number of simplifying assumptions (e.g. monoenergetic radiation, no scatter) which when included in the treatment above invalidate the general conclusions reached - see Figure 7.3. Nevertheless, logarithmic subtraction is widely applied in clinical DSA.
- Note that substantial compression of the gray scale results following direct logarithmic transformation and that multiplication of the transformed pixel values by a scaling factor is generally used to re-establish the gray scale. The term Digital Subtraction Angiography can now be appreciated to be a simplification in that to implement the technique ideally requires logarithmic transformation and multiplication as well as the subtraction of pixel values.

- Figure 7.3 illustrates the dependence of Dlog on the projected thickness of contrast medium for a range of scatter-to-primary ratios (SPRs), i.e. the ratios of the intensities of detected scattered and primary radiation. These plots were generated by including scatter contributions in the above analysis. It is seen in the figure that Dlog is reduced significantly as the SPR increases and that the dependence on projected thickness becomes non-linear. For example, it is seen that Dlog is reduced, at a projected thickness of 50 mg cm-2, by about 85% when the SPR=5 relative to the no scatter condition, i.e. the contrast of an opacified blood vessel will be reduced by this factor. In addition, it is seen that Dlog becomes relatively independent of projected thickness, above about 20 mg cm-2 when SPR=5, for example, so that the ability to discriminate different projected thicknesses, and hence vessel opacity, is significantly impaired.
- A question relevant to this discussion relates to the SPRs that are typical of clinical imaging conditions. The following table shows measured SPRs for chest radiography to illustrate the situation. It is seen, for example, that the SPR is greater than unity for all anatomical regions when no grid is employed, i.e. the scatter intensity consistently exceeds the primary intensity. It is also seen that the greatest SPR reduction is achieved when a 12:1 grid is used. Referring now to the Figure 7.3, it can be seen that scatter reduction techniques, such as the use of an air gap or a grid are therefore likely to improve the contrast of opacified vessels and that their contrast will still be substantially reduced relative to the no scatter condition.
| Imaging Technique | Lung | Rib | Heart | Mediastinum |
|---|---|---|---|---|
| No Grid | 1.22 |
1.78 |
4.26 |
10.1
|
| 30 cm Air Gap | 0.54 |
0.61 |
1.78 |
4.56
|
| 6:1 Grid | 0.59 |
0.75 |
1.7 |
3.55
|
| 12:1 Grid | 0.35 |
0.47 |
0.85 |
1.33
|
- It is apparent that this discussion is congruent with the SPR consideration in an earlier chapter regarding the imaging of bone in tissue.
- Improved scatter reduction can be achieved using computerised image processing. These include methods based on estimates of scatter fields for subtraction from patient images and those based on image Deconvolution techniques. Scatter subtraction techniques use scatter and primary measurements to compute a smooth, slowly varying scatter field, are generally cumbersome and require at least two exposures of the anatomy. In addition, subtracted images have a reduced dynamic range as a result of the discrete nature of digitised data as well as a reduced signal-to-noise ratio (SNR) because the subtraction process reduces the signal and maintains the noise.
- Image deconvolution techniques are based on Spatial Filtering processes, where a low spatial frequency content is assumed for the scatter field, and such frequencies are suppressed in the scatter correction process. This approach however suffers from a lack of exact knowledge of the actual spatial frequencies in a particular scatter field.
- It should be noted that scatter correction is critical to the successful application of Volume Tomography[26].
DSA Image Noise
[edit | edit source]- The image subtraction process is highly sensitive to the presence of noise in images - noise being increased by about 40%, theoretically, as a direct consequence of the subtraction process, due to the quadratic addition of noise variances. As a result, noise reduction techniques need to be applied in DSA imaging so as to improve the conspicuity of angiographic details. The major sources of noise in DSA images are Quantum Noise - which results from the random nature of X-ray production and System Noise - which results from the electronic components of the imaging system. The major source of system noise in XII-based fluoroscopy, for example, is generally attributed to the video camera.
- The combined contributions from these sources can give rise to a mottled appearance of regions within the images. An indicator of the quality of DSA images which accounts for this mottle is the Signal- to-Noise Ratio (SNR) of the opacified regions of images. Naturally, the SNR is high when high radiation exposures and high quality imaging components are used. However, it also has a dependence on the opacity of the region being investigated in an individual examination as well as the quantity of contrast medium present.
- The SNR can be shown, when quantum noise is the dominant noise source, to be directly dependent on the concentration of the contrast medium, ρc, and the square root of the absorbed dose at the XII entrance, DXII, i.e.
- This relationship indicates that in order to double the SNR, the concentration of contrast medium in the blood vessel can be doubled or the exposure can be quadrupled. It is apparent that both methods involve increased risk to the patient from the procedure.
- Other factors which can be shown to beneficially influence the SNR include:
- Equalisation of the transmittance throughout an image by placing, for instance, bolus materials over regions of high transmittance in order to generate a roughly similar transmittance for all regions of an image.
- Choosing an X-ray energy slightly above the iodine K-edge (i.e. above 33 keV). As a result, images with a higher SNR are likely to result when a lower kilovoltage is used (say 65 kV rather than 100 kV), to a limit imposed by the K-edge and by the output of the X-ray tube (XRT).
- It is important to note that the above consideration assumes that quantum noise dominates the noise contributed by sources from within the imaging system. This condition can be satisfied directly only by using high quality imaging components. It should also be noted that, when the system noise dominates the quantum noise (as in, for example, a fluoroscopy system with a noisy or defective video camera), increases in radiation exposure are unlikely to decrease the noise in images.
- Image noise can also be reduced using the DSA image processor. This is achieved by applying image averaging processes to the sequence of angiography images following computer acquisition and before subtraction. The simplest form of image averaging involves summing a number of images together and dividing by that number. It can be shown, based on statistical considerations, that this process reduces noise ideally by a factor of √N, where N is the number of averaged images. Thus, to double the SNR, four images should be averaged. SNR improvement can also be achieved by integrating (i.e. adding) images and by recursive filtration. This latter process can involve the application of an exponentially-weighted moving average process to angiographic image sequences. It can be shown that such filtering is more powerful than simple averaging and can give a theoretical SNR improvement of √(2N-1). Note that this type of filtering can also be applied for screening exposures providing what is sometimes referred to as Fluoro Noise Reduction (FNR). Digital noise reduction techniques are generally performed using the Image ALU component of the DSA image processor.

- The temporal-averaging feature of digital noise reduction can also be used for image presentation purposes so that the time course of the movement of contrast medium during a study can be displayed using just one image - see an example in Figure 7.4 from the peripheral study shown above - instead of a sequence of numerous images. Such an image is sometimes referred to as a Vascular Trace.
- Conventional DSA imaging can be considered to be a subset of a generalised form of image processing which is referred to as Temporal Filtration. This general approach is directed at the processing of images with respect to time so as to eliminate features which, for instance, are common to all acquired images and to enhance features which change during the time course of the image sequence. In addition, the concept indicates that image subtraction is just one mechanism, from a family of possible mechanisms, which can achieve the desired result. One disadvantage of conventional DSA, for instance, is the amount of patient dose that does not contribute to the production of a diagnostic image. At the extreme, consider a DSA image sequence that involves the acquisition of 25 images and assume that only two of these images are used to generate an image showing the blood vessels of interest. In this case, only 8% (i.e. 2/25th) of the dose is utilised and the remaining 92% is essentially wasted. Temporal filtration of the image sequence attempts to overcome this limitation by involving more than just two of the 25 images for the digital processing involved in the generation of a diagnostic image.
- One method of temporal filtration, referred to as Integrated Mask-Mode DSA involves adding (also called integrating) a number of images, acquired prior to the arrival of the contrast medium, to form an integrated mask image and adding a number of peak-opacification images to form an integrated live image. This is the process that was used to generate the vascular trace image in Figure 7.4. Thus, when four images are used to generate each integrated mask and live images, eight of the 25 images are now used in the subtraction process and, as a result, only 68% of the dose is wasted, and a subtraction image with lower noise results.
- A second method of temporal filtration, referred to as Matched Filtration, attempts to utilise all 25 images. It involves using information derived from the temporal variation in the concentration of contrast medium in the blood vessel of interest. This information can be obtained by using densitometric analysis software to plot the dilution curve for a region of the blood vessel, i.e. a plot of the time course of the contrast medium. This dilution curve is then used to define a range of weighting factors that are applied to each image in the sequence and the resulting images are simply added together. The processed DSA image has a relatively high SNR as a result of the integration of images. Further refinement of such filters can be used to colour-code parameters such as the time-of-arrival and the time-to-peak opacification, into the displayed image data. Although Matched Filtration has been shown both theoretically and experimentally to generate a DSA imaging process with good image quality and dose utilisation characteristics[27], it has not gained widespread clinical application.
DSA Instrumentation
[edit | edit source]- DSA imaging systems are generally based on integrating fluoroscopy systems with computer technology. We have considered the source of X-rays and image receptors in previous chapters. The treatment here concentrates on features of this technology which are specific to DSA.
- Figure 7.5 shows a block diagram of an imaging system used for DSA which is based on XII-video technology. It is seen that images from the video camera are fed to a digital image processor for manipulation, storage and display. In order to implement a pulsed exposure mode of operation, control connections are required between the image processor and both the video camera and the HV generator. These control connections are used to instruct the HV generator to initiate each exposure pulse and to select the appropriate mode of operation of the video camera. Systems frequently include a variable optical aperture between the XII and the video camera. Note that this device is not included in the figure for reasons of clarity.

- The intense radiation exposures used for pulsed exposure DSA generate relatively bright images at the XII output. Since such bright XII images are likely to saturate the video camera (which typically has a high sensitivity to light), the optical aperture is generally used to control the illumination of the target of the video camera. The aperture is set wide when fluoroscopic exposures are used for patient positioning purposes and narrowed during the DSA exposures. The exact setting of the aperture is dependent on the particular examination and is generally set automatically by the digital image processor.
- High power X-ray generators and XRTs are required for DSA. Hence, generators are used which, for instance, can produce exposures up to 100 kV, 1000 mA with very short exposure times and XRTs are used which are of high heat capacity and small focal spots, e.g. 0.5 mm. The generator should also be capable of generating low, continuous exposures for catheter guidance and patient positioning purposes.
- Special-purpose video cameras are required for pulsed exposure DSA. One factor influencing their design results from the need for low noise components, as discussed earlier. This can be achieved using cameras with electron guns based on diode configurations. Such designs allow relatively large electron currents to be used for scanning the target of the video camera and results in low noise images. It has been found that video cameras with SNRs of the order of 60 dB (1000:1) are required.
- A second factor influencing the design of video cameras for pulsed exposure DSA results from a requirement to generate images of good temporal resolution. Thus, the camera target should be of made from low persistence or, in other words, low lag, materials. Such a target can be obtained using lead oxide, as in the Plumbicon cameras. An added advantage of using this type of target is its transfer characteristic with a gamma of unity - which is advantageous for the subsequent mathematical processing of images.
- A third factor influencing camera design is the specialised scanning mode used for reading the target with the electron beam. Both interlaced and progressive scanning are used, as described earlier.
- Finally, high resolution video cameras have found application in DSA. These include 1049-line plumbicons and CCD cameras generating 1024 x 1024 x 10 bit images at up to 25 frames per second (fps) and 2099-line plumbicons generating 2048 x 2048 x 10 bit images at up to 7.5 fps.
DSA Image Processor
[edit | edit source]- A block diagram of a DSA image processor is shown in Figure 7.6. It is seen that video signals from the XII-video image receptor are digitised using an analogue-to-digital converter (ADC) and the resulting digital data is passed through an Input Look-Up Table (ILUT) prior to storage in one of the image memories. The ILUT is generally used to logarithmically transform acquired images. It should be noted that in some system designs, logarithmic processing is performed using a look-up table between the image memory and the ALU so that displayed unsubtracted images appear in their conventional non-logarithmic format while subtracted images have the log transformation applied.

- At least three image memories are required for routine DSA - one for each of the mask and live images and the third for the subtracted image, although most systems have the capacity for storing more than three images. Image subtraction is performed using an arithmetic/logic unit (ALU) with the subtracted image data being fed along the Feedback Path so that it can be stored in image memory. The ALU can also be used for averaging images for noise reduction purposes.
- The type of image processor shown in the figure can also be used to implement a number of variations on the basic theme of DSA imaging. One of these variations is referred to as Time- Interval-Difference (TID) Imaging, which involves periodically updating the contents of the mask image memory during the DSA study. This approach allows short-term changes between images to be displayed and therefore lends itself to imaging fast moving events, such as cardiac contractions.
- A second variation on the theme involves acquiring images of both the arterial and the venous vessels in the same region of the patient (e.g. the carotid arteries and jugular veins in the neck) so that when a mask image in the arterial phase is subtracted from a live image from the venous phase, a subtracted image showing both arterial and venous vessels can be generated. A third variation is referred to as Roadmapping - see Figure 7.7 - where an image at peak opacification is used as a mask and subsequent subtraction images, without injection of additional contrast medium, are used to guide advancement of a catheter or guide-wire.

- A number of image manipulations specific to DSA include:
- Remasking: This process is used to reduce motion artifacts in subtracted images which result when the patient moves between acquisition of the mask and live images - see Figure 7.8. The process generally involves interactively choosing a more suitable mask image following image acquisition, so as to minimise the contribution of motion artifacts in the displayed DSA image.
- Reregistration: This process is also used to reduce motion artifacts in DSA images and is commonly referred to as Pixel Shifting. The process involves spatially shifting the mask image in small increments relative to the live image so that improved registration of features which are common to both images is achieved. Vertical and horizontal shifts, of the order of a fraction of a pixel, are possible under operator interaction. An array processor can be used to perform the necessary calculations and image shifts at the required speeds. Because of the complex nature of projected body movements, however, simple vertical and horizontal shifting is unlikely to remove all motion artifacts from images. However, the approach is generally useful for isolated regions within images.
- Landmarking: This process is used to provide anatomical landmarks in the subtracted images. It is generally achieved by subtracting not the full live image, but a fraction of its intensity (e.g. 90%), from the mask image.
- Spatial Enhancement: This process is used to improve the cosmetic appearance of subtracted images so that edges of blood vessels are displayed with increased prominence (e.g. edge enhancement) or sharp transitions in images are suppressed (e.g. image smoothing). An array processor can be used to perform the necessary calculations at high speeds.

- Quantification: This process is used to extract quantitative information from DSA images. The general-purpose computer with dedicated software is used for this purpose. Two general approaches have found application. One approach is referred to as Geometric Analysis and involves measuring the number of pixels between points of interest in an image or the number of pixels within specified areas of the image. On this basis, for example, a stenotic region in a blood vessel can be referenced to a non-stenosed region of the vessel or the projected area of the left ventricle can be compared in systolic and diastolic images. In addition, following appropriate image calibration, distances can be computed in conventional units of measurement (e.g. mm or cm). The second approach is referred to as Densitometric Analysis and involves computing the mean pixel value in opacified regions of images. Cardiac ejection fractions and stenoses, for example, can also be assessed using this approach. Both of these approaches generally rely on accurate determination of the edges of blood vessels and cardiac chambers. For this reason, most quantification software also includes features which aid in reproducible edge localisation. Note that both geometric and densitometric analysis can also involve significant measurement artefacts. In the geometric case, these primarily result from the spatial distortion introduced by the imaging process. In the densitometric case, they mainly result from contributions from scattered radiation and veiling glare - so that, as discussed earlier, correction techniques need to be applied in situations where accurate measurements are required.
- Additional processes involve Bolus Chasing, Rotational Angiography and Volume Tomographic Angiography. Bolus Chasing[28] has been found to be particularly helpful in peripheral angiography, for example. Here, the progress of the contrast medium is tracked automatically and used to increment the table and/or XRT/image receptor movement to the next anatomical region. The subsequent set of subtraction images can then be used to construct a composite image of the peripheral vasculature. In Rotational Angiography[29], a C-arm assembly, for example, can be caused to rotate at 10 - 30 degrees per second during the imaging sequence. Subsequent dynamic display of the subtraction images can be used to generate a perceived 3D presentation so that complex relationships within the vasculature can be more readily appreciated. Volume Tomographic Angiography[30] is similar to Computed Tomography (CT) where the C-arm is rotated around the patient during the imaging sequence. The image data is subject to a volume reconstruction algorithm which permits generation of three-dimensional images of the opacified vasculature. We will consider this latter process in more detail below.
Cone-Beam Computed Tomography
[edit | edit source]
Conventional radiography is based on the attenuation of an X-ray beam by different tissues and is used to project a shadow onto an image receptor. Essentially, these images are projections of a 3-D object onto a 2-D plane. Small lesions are therefore not readily identified, image distortion results because of unequal magnification effects and since scatter contributes substantially to the image formation, low contrast masses are poorly delineated. Further, as illustrated in Figure 7.9, there is a degeneracy introduced into the image, i.e. two anatomically quite different objects may produce the same image contrast because the effective attenuation they each produce is identical. In short, there is a considerable loss of information.
This situation can be improved using Computed Tomography (CT). This was originally developed as a radiographic technique for producing cross-sectional images by scanning a slice of tissue from multiple directions using a narrow fan-shaped X-ray beam. The attenuation of each tissue element is calculated and converted to be shown as shades of grey on a display monitor. The basic principle of CT-scanning is that the internal structure of an object can be reconstructed from multiple projections of that object. Johann Radon established this principle, as early as 1917 and Allan Cormack published work on image reconstruction in 1963 and 1964. In the early 1970s, Godfrey Hounsfield applied these concepts using computer technology and used it for diagnostic imaging[31]. And the rest as they say is history!
We'll start our treatment here with a consideration of the formation of an image of a single tomographic slice and then extend these concepts to describe cone-beam tomography.
Image Reconstruction Basics
[edit | edit source]
- A cross-sectional layer called a tomographic slice of the body is obtained by dividing it into many tiny volume elements called voxels - see Figure 7.10. When displayed on a computer screen, each voxel is represented in two dimensions by a pixel. The task in CT is to assign a number to each voxel that is proportional to its X-ray attenuation. This can be achieved by rotating an XRT and an array of detectors around the slice of interest to measure the radiation intensities projected at different angles around that slice. In other words, multiple views around the slice are acquired. An image reconstruction algorithm is then applied to this projection data to estimate the attenuation in each voxel. The amount of attenuation for a voxel is determined by its composition and size, along with the X-ray energy, and is characterised by a parameter (which can be expressed in Hounsfield Units, HU) derived from the linear attenuation coefficient, μ.
- There are a number of image reconstruction methods that can be applied. However, the one that is of interest to us is called Filtered Back Projection (FBP).

- A basic premise in back-projection is that any attenuation of the X-ray beam has occurred uniformly along the path followed from the source to the detector. Let's consider a simple tomographic slice containing just four voxels to illustrate the computational approach - see Figure 7.11. The first projection, P1 is obtained from a horizontal exposure from left to right in the figure. The back-projection of P1 involves putting the values 7 and 9 in both elements of the first and second rows, respectively. The second projection, P2 adds a 4 to the top right element, 1 to the bottom left element and 11 to the other two elements when it is back-projected. The other projections are treated in a similar fashion. Following regularisation of the data set the final image is obtained at the bottom left of the figure.
- The representation in Figure 7.12 demonstrates the principle in action. A single projection is back-projected to give a dark stripe across the entire image plane - see panel (a). As the phantom is scanned from different angles and the projections back-projected onto the image plane from many directions, an image of the radio-opaque object begins to emerge - see panel (b). As the number of projections increases, the quality improves but there will always remain streaking as seen in panel (c). A certain amount of spurious background information remains which can severely degrade the quality of reconstructed images. In mathematical terms, the image is blurred because of a convolution with a 1/r functional dependence on distance, r. In other words, the point spread function (PSF) has a 1/r dependence which is totally attributable to the back projection process.

- Image quality can be improved substantially using a modified form of back-projection called Filtered Back Projection (FBP). In this technique - see Figure 7.13 - projection data is first filtered spatially to account for the effect of sudden density changes which cause the streaking in simple back-projection. The filter is referred to as a convolution filter or kernel. The procedure can be performed in the spatial frequency domain using Fourier Transform (FT) methods or directly with spatial domain processing. After the convolution process, the data for each projection is inverse Fourier transformed before the back projection computation is undertaken. In practice the task of image reconstruction is performed using special array processors and dedicated hardware, which aids in speeding up the reconstruction task.


- A choice of filters can generally be selected to enhance either soft tissue features in the image or bone detail. Indeed, the image can be post-processed using a different filter after the scan has been completed if needed. Images can be generated to enhance bone detail or display subtle low contrast masses without the need to re-scan the patient. The filter choice therefore has a major impact on image quality. The two most common filters used in X-ray CT are those due to Ramachandran & Lakshminarayana (commonly called the Ram-Lak) and Shepp & Logan. Viewed in spatial frequency space, the former is essentially a ramp filter with a cut off frequency and the latter combines a smoothing filter with the ramp to attenuate high frequency noise. The ramp filter compensates for the artefacts introduced by the simple back projection process but does not compensate for the increasing noise content of the data with increasing frequency. Images of an axial tomogram reconstructed with a soft tissue and with a bone algorithm can be seen in Figure 7.14.
C-Arm CT
[edit | edit source]- C-arms fluoroscopy systems can implement back-projection using images acquired at different angles around the patient[32]. The X- ray beam is collimated to a large cone with an XRT and image receptor rotated as one to acquire projections from a large number of slices simultaneously. An approximate back projection reconstruction technique known as the Feldkamp algorithm is generally applied. The result is a full 3D image acquisition in a single rotation about the patient. Multi-Detector CT (MDCT) scanners use this approach with an array of detectors (e.g. 64 rows and 800 columns) - and are sometimes referred to as Multi-Detector Row scanners. C-arm fluoroscopy systems also use a broad-area image receptor but of much larger size, e.g. 1,920 dels in 2,480 columns.

- C-arm systems can therefore acquire data simultaneously for a much larger number of projections. A disadvantage, however, is that imaging with broad-area exposures generates a substantial amount of scattered radiation[33] so that tomographic images do not have the resolving capacity for low subject contrasts that is achievable with MDCT. Computerised scatter corrections are therefore applied to address the issue. Another disadvantage is that the Feldkamp algorithm only performs well for small fields of view, e.g. the head and neck. Its application to larger body areas involves handling truncated projections, which can be addressed using more sophisticated computational methods[34].
- Similar designs have also found application in dental radiography[35].
- The imaging geometry for C-Arm CT is illustrated in Figure 7.15. The XRT and image receptor take images from different angles around the patient at a magnification of ~1.5. Partial rotations of 150-200o have been found to be adequate - not the full 360o as in helical CT. In addition, rotations can be in orbital as well as oblique planes. Rotation speeds of 30o per second and imaging frame rates of 7.5-10 frames per second are typically used to acquire 50 or more 2D projections.
- In neuroangiography, the data acquisition typically involves two rotational runs - one pre- and the other post-contrast injection. The pre-contrast acquisition is called the Mask run, while the post-contrast one is called the Fill run. The resultant 3D datasets can be subtracted (similar to DSA) to form the contrast medium data that is used for image reconstruction. Quite detailed images of the cerebral vasculature can be generated, as illustrated in the following movies.
- 3D Roadmapping can be achieved using this technology by superimposing live 2D images on top of a MIP projection of the opacified blood vessels. Sophisticated systems can be interfaced to allow guidance, for instance, for electronic surgical tools. However, these topics are beyond the scope of this wikibook.
Multi-Detector Computed Tomography (MDCT)
[edit | edit source]The evolution of MDCT from the days of Computerized Axial Tomography (CAT) is illustrated in Figure 7.1.5.1. Hounsfield's original parallel pencil-beam, translation-rotation scanning was improved with narrow fan-beam scanners (2nd generation) and later with broad fan-beam, rotation-rotation scanning (3rd generation). Images were acquired in the axial plane in the early EMI Scanner designs using simultaneous acquisition of two slices of thicknesses of 8-13 mm per scan. Scan times for the head were about 5 minutes with the scanner generating non-contiguous 180° scans with the patient table incrementally stepped through the anatomical region of interest. The third generation design incorporated a curved, linear array of up to 896 detector elements (dels), each ~1 mm apart, and a fan-shaped X-ray beam which totally encompassed the patient's body. This resulted in substantial decreases in scanning times. The XRT and detector array were rotated around the patient at high speeds to irradiate slices of anatomy of thickness 1-10 mm. Furthermore, excellent contrast differentiation was achieved using pre- and post-patient collimation. In addition, bow-tie shaped filters, chosen to suit the body or head shape, were used to equalise exposures and to reduce patient dose in the periphery of the field of view.
 |
 |
 |
 |
A number of extensions to the 3rd generation design were developed because projections collected from opposite sides of the patient ideally generate the same projection data. In other words, half the scan data was redundant. These developments included the Flying Focus XRT where the electron beam could be switched alternately between two discrete focal spots during the acquisition of each projection. The foci were displaced from each other on the anode by half a del spacing. On this basis, the number of independent projections (or, equivalently, the number of dels), could be doubled by interleaving data from the two projections. One scanner design could increase the effective number of dels from 768 to 1,536 using this technique.
Scatter levels are relatively low in CT, given the narrow-beam geometry, compared to those in 2D projection radiography. This feature has allowed application of densitometric analysis to assess brain perfusion[36] and to evaluate trabecular Bone Mineral Density (BMD) in the lumbar spine, for example[37] in Quantitative Computed Tomography (QCT).
CT Image Display
[edit | edit source]- Following computation of the linear attenuation coefficient for each voxel in a slice using filtered back projection (FBP) reconstruction, the values are normalised to the value for water as a reference, scaled and presented as a Hounsfield Unit, HU, also called the CT-number, as follows:
- where μm and μwater are the linear attenuation coefficients for the tissue material and for water, respectively. The CT-number of water is therefore zero. CT-numbers for a number of tissues are shown in the table below.
| Tissue | CT-Number (HU) |
|---|---|
| Lung | -300 |
| Fat | -90 |
| White Matter | 30 |
| Gray Matter | 40 |
| Muscle | 50 |
| Trabecular Bone | 300-500 |
| Cortical Bone | 600-3,000 |
- Reconstructed images can be presented on a computer screen using a grey scale. The grey scale can be chosen to encompass all or some part of the entire range of CT-numbers by selecting a suitable window level and window width. The window width is the range of CT-numbers selected for display and the window level is generally the central CT-number about which the window is chosen. Typically, the highest number is assigned to white and the lowest number to black with all intervening numbers assigned intensities on a linear scale. Air can therefore be displayed as black with cortical bone appearing relatively bright.
- Examples of image display manipulation are shown in the two figures above. In Figure 7.15.2, the same image of a slice through a patient's liver is displayed using a relatively narrow window (high contrast) and also with a wide window. The image with the narrower window appears noisier, but this is merely a reflection of the fact that the gray scale is spread over a narrow range of CT-numbers.
- Figure 7.15.3 illustrates the use of a relatively narrow window to highlight pathology in the lungs.
Helical CT
[edit | edit source]
- Helical scanning, as illustrated in panel (d) of Figure 17.15.1, was developed on the basis of continuous movement of the patient table along the cephalocaudal direction (z-axis) of the scanner. Axial slices were generated through interpolation along the z-axis prior to Filtered Back-Projection (FBP) reconstruction. Table speeds of 1-10 mm/s and complete 360° rotations were achieved in half a second or less with the fan beam collimated to 1-10 mm thick. A new scanning parameter called the Pitch was introduced, which defined the ratio of the table movement distance in a single rotation to the slice thickness. A table movement distance of 10 mm and a slice thickness of 10 mm would therefore generate a pitch of unity. Pitch values of 0.5-2 were used depending on the desired spatial resolution along the z-axis, with those less than one, e.g. 0.8, providing adequate over-lapping slices for 3D visualizations. No gaps in the data set occurred as the anatomy was being scanned, which can be contrasted with conventional axial scanning where inter-slice gaps result unless contiguous slices are specifically chosen to be scanned.
- Because of the relative motion between the patient table and the gantry, the effective slice width given by the Slice Sensitivity Profile (SSP) was greater than the nominal slice width because the slice profile is blurred by a convolution with a triangular profile attributable to the table motion - see Figure 7.15.4. Software advances using z-interpolation techniques were then applied to minimise this broadening of the SSP[38]. Linear Interpolation could be applied, for example, to both 180o and 360o sequences from adjacent helical scans to give the so-called 180LI and 360LI, or Slim and Wide, processing algorithms. However, regardless of the interpolation technique employed increasing the pitch led to increased effective slice widths.
- A significant reduction in examination times resulted since large sections of the anatomy could be scanned rapidly and contiguously with little influence from patient motion. For example, up to 80 slices could be scanned contiguously in 60 seconds of non-stop scanning - see an example in Figure 7.15.5. Single breathhold scanning became possible on this basis. Furthermore, isotropic voxel dimensions, i.e. of equal size in all three axes, could be generated, instead of the rectangular-shaped voxels of single slice scanning, and reconstruction of sagittal, coronal, curved planar, off-axis and 3D images became feasible. Within the scanned volume, images could be reconstructed at arbitrary positions and spacings with slice widths controlled through collimation. One important difference was that the position and spacing of successive slices chosen for reconstruction could be made retrospectively without the need to re-scan the patient. Thin slices (e.g. <3 mm) could be generated with an overlap of 80%, for instance, for the reconstruction of exquisite 3D images.
Multi-Slice CT
[edit | edit source]- Scanning speed increases for volume imaging subsequently generated technical advances such as multi-detector scanning (MDCT). Initially, about year 1998, four slices of thickness 0.5-10 mm were able to be scanned simultaneously using a 2D detector array with a z-axis length of 20-32 mm - see Figure 7.15.7. Scanner rotation times of half a second or less were achieved by mounting the XRT, the HV generator and the detector array on the same rotating gantry, for instance. The speed improvements, along with reductions in tube loading, were found to result in only a modest increase in patient dose. On this basis, techniques such as ECG-gated cardiac studies, coronary artery calcification scoring, Virtual Colonoscopy and CT Angiography (CTA) were developed.
- It should be noted that the original EMI Scanner used two pencil-beams and hence was a 2-slice scanner - and therefore could be considered to be the first multi-slice scanner.
- Algorithms for axial interpolation from helical scans were developed such as Multi-Slice Linear Interpolation (MLI), e.g. 180MLI and 360MLI, and were enhanced using z-filtration processes which applied an adaptive axial interpolation such as Multi-Slice Filtered Interpolation (MFI), e.g. 360MFI.

- The 2-D detector arrays are solid-state devices and the simplest example is the Matrix Array, as illustrated in Figure 17.5.8. The array can consist of 912 columns by 16 rows, for example, of identical dels, each 1.25 mm square, curved to fit the arc of the XRT rotation. Eight of these columns are shown, in panel (a) of the figure, being irradiated by an X-ray beam of width 6 mm, with the result that data for four 1.25 mm axial slices can be acquired simultaneously. More rows, up to sixteen in this case, can be irradiated simultaneously with this arrangement when the X-ray beam is broadened to encompass the width of the detector array. Flexibility can be built into this design by coupling the outputs of adjacent detector rows, as illustrated in panels (b), (c) and (d), where the outputs of 2, 3 and 4 rows, respectively, are summed to simultaneously generate four 2.5 mm thick slices, or four 3.75 mm slices, or four 5 mm slices.
- A more flexible design is provided by the Adaptive Array detector, as illustrated in Figure 7.15.9. Rather than columns of square detectors, this array uses columns of detectors of variable width, such that the width in the two central columns is relatively narrow, e.g. 1 mm as in the figure, with the column width increasing towards the periphery, e.g. from 1.5 mm, through 2.5 mm to 5 mm as shown in the figure.

Fig. 7.15.10: Illustration of four modes of multi-slice acquisition for an adaptive array CT detector.
- Four modes of operation of this type of detector array are shown in Figure 7.15.10. It can be seen in panel (a) that two 0.5 mm slices can be acquired when a 1 mm thick X-ray beam is aligned with the central columns of the adaptive array. In panel (b), four 1 mm slices can be acquired using a beam of thickness 4 mm. Detector coupling is illustrated in panels (c) and (d), where the outputs of detectors in the four central columns are coupled so as to simulate two 2.5 mm wide detection columns, and hence acquire data for four 2.5 mm slices.
- A second advantage of the adaptive array is that the number of individual dels on each row can be considerably reduced, from 16 to 8 in the case we've just discussed. This adds greatly to the speed with which data can be generated by the array and reduces the number of computations necessary for uniformity and other corrections that must also be applied to the measured data.
Multi-Detector CT
[edit | edit source]- Z-axis coverage was increased and scan times reduced even further with the development of MDCT systems with, for instance, 16- (in the year 2001), 64- (in 2004), 128- (in 2005) and even 320- (in 2007) slice capabilities. Fan beam CT evolved into Cone-Beam CT on this basis, where the X- ray beam is collimated to a rectangular cone so that a rotating XRT/detector assembly can generate image data from multi-slice helical scans[39]. Furthermore, scanner rotation speeds as quick as 0.3 seconds or less allowed 3D images of the heart to be captured in motion, at 0.25 mm slice thickness, adding a 4th dimension (4D).
- The gantry is an important design element of the CT scanner, where its rotating components are subject to the high centrifugal forces associated with very fast rotations. Forces up to 10 G can be experienced, for example, with rotations of radius, 40 cm, and rotation speeds of less than half a second. Precise balancing is therefore needed, especially when the gantry is tilted for oblique acquisitions.
 |
 |
- CT is acknowledged to be one of the more demanding X-ray tube applications. Most particularly, with the advent of single breathhold imaging of up to one minute, the X-ray tube and housing must be capable of quickly dissipating enormous heat loads. For example, an X-ray tube operated at 133 kVp and 250 mA for 60 seconds deposits ~2 MJ of energy in the anode. Cooling rates can be enhanced through the use of heat exchangers, for example, and software generally limits misapplication of the XRT.
- An XRT design which used liquid metal bearings to increase anode rotation speeds was introduced, but a major design breakthrough was achieved with the development of the Rotating Envelope XRT. Here, the electron beam can be focussed and deflected inside a small rotating metal tube using external electromagnets[40]. Exceptional cooling rates have been obtained with the STRATON XRT, for example. In addition, precise control of the electron beam has allowed implementation of the Flying Focus principle in the z-direction. As a result, 64 slices of 3 mm thickness can be generated from two 32 slice, 6 mm thickness, simultaneous acquisitions, for example. However, fewer photons reach the detector per exposure with this technique because the photons are divided between the two focal spots.
- Both pre- and post-patient collimation of the X-ray beam is generally used to reduce scattered radiation. Modern detectors can be made using strips of phosphor materials, e.g. CdWO4, Gd2O3 and Gd2O2S, coupled to a-Si photodiode arrays. Ultra-Fast Ceramic (UFC) detectors are manufactured from doped gadolinium oxysulfide in the form of a polycrystalline wafer. These devices feature a relatively fast response, which improves the sampling rate, as well as high detection efficiency and broad dynamic range. Both matrix and adaptive arrays can be used in 64-slice scanners.
- A patient positioning system is typically used for the generation of accurate position data for the subsequent reconstruction process, especially during helical scanning. This system can also allow the patient to be positioned at the isocentre of the scanner and the area of the patient for irradiation is generally indicated using laser beams.
- Forms of image reconstruction that are in clinical use include:
- Rebinning Algorithms: These include algorithms optimized for small cone angles as in 64-slice CT, e.g. Advanced Single-Slice Rebinning (ASSR). The computation reduces three-dimensional cone-beam data to tilted 2D slices by minimizing the deviation of the reconstruction plane from the spiral for each reconstruction position. It has found application in both 16-slice and 64-slice CT scanners. The data are then sorted into angulated axial slices using filtered back projection (FBP). These oblique slices are finally interpolated to parallel axial slices. Examples are Adaptive Multi-Planar Reconstruction (AMPR) and Weighted Hyperplane Reconstruction (WHR) which can be implemented at relatively high speeds using dedicated hardware.
- Approximate Algorithms: These are generally extensions of the Feldkamp algorithm for 3D filtered back-projection to multi-slice helical scanning. Parallel axial images are obtained directly from the raw projection data. Examples include the Cone-Beam Reconstruction Algorithm (COBRA) algorithm and the True Cone-Beam Tomography (TCOT) reconstruction and require considerable processing power to implement at high speeds.
- Most reconstruction algorithms require 180o projection data for reconstruction of the first and last image in helical acquisitions to ensure reconstruction of the anatomical section of interest. This process is known as Over-Ranging and it contributes to the overall patient exposure. Its contribution is relatively high when a small volume is scanned using a low pitch, e.g. inner ear examinations. Adaptive pre-patient z-collimation can be used to reduce this effect by using opposing collimator blades which automatically open at the start of the helical scan and shut at the end.
- Automatic Exposure Control (AEC) is generally implemented by modulating the mA depending on the size, shape and composition of the patient's anatomy so as to keep image noise constant through the scan. Both in-plane (xy-axis) and longitudinal (z-axis) mA modulation are used.
- Cardiac images can be acquired using 64-slice, helical MDCT scanning with slow table movements so that projection data from 180o gantry rotations can capture sufficient image data in both space and time, even in patients with irregular heart beats[41]. ECG-gated acquisitions with a pitch of 0.15-0.25 can be used, with a consequent increase in radiation dose, although prospective-gating of acquisitions can also be used which provide reductions in patient exposure. Scanning with a 320-slice system can be used to overcome these type of issues by direct coverage of the whole heart. Further details on cardiac CT are beyond the scope of this wikibook and the interested reader is referred to Halliburton (2009)[42] for further details.
- Finally, improvements in temporal resolution can be achieved using Dual-Source MDCT with two XRTs and two detector arrays mounted at right angles to each other in the CT gantry[43]. Its application to cardiac imaging provides significant advantages[44].
CT Fluoroscopy
[edit | edit source]- CT Fluoroscopy (CTF) has also been referred to as Continuous CT or Real-Time CT since it involves generating tomographic images at sufficiently high frame rates to allow guidance of needle placement in small or deep-seated lesions. Applications can include biopsy of thoracic lesions, biopsy/drainage of pelvic lesions, vertebroplasty and drainage/aspiration of intracranial haematomas. The advantages of CTF include increased target accuracy and reduced procedure times[45].
- The major difference to a conventional CT system is that high speed reconstruction techniques are applied, and that an operator panel, exposure footswitch and image monitor are installed in the scanning room for use by the interventionist. Controls are generally available for table movement, gantry tilt, laser grid definition and fluoroscopic factors. The other significant operational change relates to the choice of tube current which is typically 30-50 mA in CTF. This should be compared with typical screening currents used in conventional fluoroscopy of up to 5 mA, so that CTF can be regarded as a high dose procedure. In this context, additional beam filtration can be introduced automatically for CTF procedures to reduce patient exposure by up to 50%, for example. Furthermore, the use of protective gloves and needle holders can reduce the radiation exposure to the hands of the interventionist.

- The fast reconstruction algorithm first applied for CTF used a partial (or incremental) reconstruction technique. It exploits the fact that each image in a sequence of CTF images contains a significant amount of data from previous images in that sequence, since the same slice is being scanned continuously. The image reconstruction process is as follows:
- raw data from the first 360o rotation is reconstructed by filtered back-projection and displayed;
- after the next No of scanning has been completed, the same processing is performed and is used to update the displayed image; and
- the process is repeated continuously during the procedure.
- The value of N is typically 30o, 45o or 60o, with frame rates of 12, 8 and 6 frames per second, respectively. In the case of 60o updates and 6 frames per second, the delay between each image is 0.17 seconds. A Last-Image-Hold (LIH) technique can be used while the image is being updated with the resulting time lag being considered by the interventionist in terms of biopsy technique. Example images are shown in Figure 7.15.11. The display of three adjacent slices of thickness 5 mm with MDCT scanning can be used to improve visual feedback to the interventionist as the needle progresses. In addition, multi-planar reconstructions (MPR) and volume rendered 3D images can be used to enhance fine control.
- Iterative reconstruction can also be applied for CTF to improve image quality and reduce patient exposure. Furthermore, techniques such as Angular Beam Modulation (ABM), where the X-ray beam is switched off for 120o during the XRT rotation proximal to the injection site, result in considerable reductions in patient dose as well as the dose to the hands of the interventionist[46]. Lead drapes on the patient to decrease scattered radiation and mobile radiation shields can be used for additional radiation protection.
Iterative Reconstruction
[edit | edit source]- This was the method employed in the original EMI scanner but was superseded by faster analytical techniques such as Filtered Back Projection (FBP). Computer hardware and algorithm developments in the first decade of the 21st century, however, have enabled the rebirth of iterative reconstruction in clinical application of Computed Tomography.
- The reconstruction process is illustrated in Figure 7.15.12 for a simple image consisting of a 2x2 pixel matrix. It starts with a guess of a solution and then compares the actual projections with the ones obtained on the basis of the guess. Modifications are made to the pixel values and the procedure is repeated. Repetitive iterations are made until the differences between the measured and calculated projections are insignificant.
- The first estimate of the image matrix is made by distributing the first projection, P1, evenly through an empty pixel matrix. The second projection, P2, is then compared to the same projection from the estimated matrix and the difference between actual and estimated projections is added to the estimated matrix. The process is repeated for all other projections.
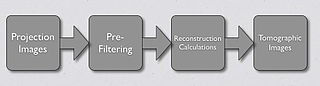
- The overall FBP process is illustrated in the following diagram:
- Developments in reconstruction algorithms such as Adaptive Statistical Iterative Reconstruction (ASIR) are based on using FBP images themselves for the initial guess and subsequently blending both FBP and IR reconstructions[47]. ASIR and similar algorithms, e.g. Iterative Reconstruction in Image Space (IRIS), are able to selectively identify noise so as to subtract its contribution from the image data and generate CT scans of superior quality to FBP. This feature can be exploited for dose reduction and substantial decreases, e.g. 23-66%, have been reported[48]. Another approach is referred to as Model-Based Iterative Reconstruction where a physics model of the CT imaging process is incorporated into the iterations. Both these approaches are compared in Love et al (2013)[49] and Stiller (2018)[50].
- Many of these computations are based on the Maximum-Likelihood Expectation-Maximisation (ML-EM) algorithm where a division process is used to compare actual and estimated projections, as shown below:

- One cycle of data through this processing chain is referred to as one iteration. The Ordered-Subsets Expectation-Maximisation (OS-EM) algorithm can be used to substantially reduce the computation time by utilising a limited number of projections (called subsets) in a sequential fashion within the iterative process. Noise generated during the reconstruction process can be reduced, for example, using a Gaussian filter built into the reconstruction calculations or applied as a post-filter:

As a final point, it should be appreciated that the concepts behind many contemporary developments in Computed Tomography, except helical scanning, have their origins in work done in the early days of its clinical application[51].
Dual-Energy Radiography
[edit | edit source]Dual-energy imaging can be used to eliminate bone information in an image, so that an image displaying tissues only is obtained. Alternatively, the technique can be used to generate the reverse effect where tissue information is eliminated and an image displaying bone only is generated. This latter option ideally allows the density of bones to be analysed. A theoretical background to this imaging technique will first be developed below with the discussion leading towards Dual-Energy X-Ray Absorptiometry (DEXA).
Basic Dual-Energy Physics
[edit | edit source]
- Dual-energy imaging is based on exploiting the difference in the attenuation of tissue and bone - see Figure 7.16 - at different X- ray energies. It generally involves acquiring images at two X-ray energies and processing them to suppress either the bone or the tissue information. A simplified mathematical model, similar to that developed earlier earlier for DSA, assumes that monoenergetic radiation is used and no scattered radiation, once again, is detected, so that the transmitted radiation intensity through a region of bone and tissue, acquired at a low X-ray energy and following logarithmic transformation, can be given by:
- where:
- μtl is the linear attenuation coefficient of tissue at the low X-ray energy,
- xt is the tissue thickness,
- μbl is the linear attenuation coefficient of bone at the low X-ray energy, and
- xb is the bone thickness.
- Similarly, the transmitted radiation intensity for the same region of an image acquired at a higher X-ray energy is given by:
- where:
- μth is the linear attenuation coefficient of tissue at the higher X-ray energy, and
- μbh is the linear attenuation coefficient of bone at the higher X-ray energy.
- When these images are multiplied by separate weighting factors, kl and kh, and the result combined to form a composite image, the result is given by:
- Therefore
- which suggests that tissue cancellation can be achieved by setting the coefficient of xt equal to zero, i.e.
- We can re-write this equation to get:
- and therefore:
- which indicates that tissue can be eliminated from the composite image when the ratio of weighting factors are chosen to equal the negative of the ratio of the attenuation coefficients of tissue at the two X- ray energies. A similar approach can be used to effect bone cancellation by setting the coefficient for xb to zero.
Dual-Energy Imaging
[edit | edit source]- CR and DR image receptors can generally be used for dual-energy radiography in either of two configurations:
- Dual exposures: where two separate exposures are used in applications where patient movement isn't an issue; and
- Single exposure: where two imaging plates separated by a filter are mounted in a dual-energy cassette to record the low energy image on the anterior plate and the high energy image on the other.
- The form of image data processing is illustrated in Figure 7.17.
- A chest radiograph acquired at 56 kV is shown in the top left panel of the figure. This is referred to as a low energy image. In the top right panel is a radiograph of the same patient's chest acquired at a high energy - 120 kV, with 1 mm copper filtration. Results of the dual-energy processing are shown on the bottom row. The bone-subtracted image is shown in the bottom left panel and the tissue-subtracted image in the bottom right panel. Notice that the tissue-subtracted image demonstrates that the lesion in the patient's left lung is a calcified nodule, since it doesn't appear in the bone-subtracted image. Simulated X-ray spectra for the two different kilovoltages are shown in Figure 7.17a to illustrate the energy separation that can be achieved using these exposure factors.
 |
 |
|---|---|
 |
 |
- Similar techniques to these have also been developed for Dual-Energy Computed Tomography (DECT)[52] and can be used to discriminate between the compositions of different types of renal calculi[53] and the evaluation of pulmonary nodules[54], for example. It is also referred to as Spectral CT.
- DECT provides the ability to differentiate between tissue, bone and contrast media using CT acquisitions at two different X-ray energies by adjusting the blending of the two sets of raw CT data before the images are reconstructed. A number of approaches to generating these datasets have been developed:
- Dual-source CT: two X-ray tubes with different kilovoltages and beam filtration (see Figure 7.17b for example spectra),
- Single-source CT with rapid switching between two kilovoltages with a single X-ray tube,
- Single-source CT with dual-layer detector with yttrium-based scintillator for low energies and gadolinium-based scintillator for high energies (see Figure 7.17c for comparative attenuation data),
- Single-source CT tube with split filter,
- Single-source CT with sequential dual-energy scans and image spatial registration.
- An overview of these techniques and their clinical application is provided in Goo & Goo, 2017[55].
DEXA Instrumentation
[edit | edit source]- Dual-Energy X-ray Absorptiometry (DEXA) has its origin in a nuclear medicine procedure where transmission for two gamma ray energies was used to determine bone mineral density. The procedure is referred to as Dual Photon Absorptiometry and typically used the isotope 153Gd, which emits gamma rays at 44 and 100 keV. As a result of limitations in photon flux and practical considerations, the radioactive source has been replaced by an X-ray tube in the DEXA technique. This technique has found widespread clinical application in the assessment and monitoring of osteoporosis and has surpassed the main alternative technique, Quantitative Computed Tomography (QCT) in terms of accuracy, precision and radiation dose.

- Two general approaches to generating the appropriate X- ray energies have been developed. In one technique, the kilovoltage and filtration are switched rapidly during image acquisition, e.g. from 70 kV and 4 mm Al filtration to 140 kV with an additional 3 mm Cu filter. In the second technique, a single X-ray energy with two different filters is used, e.g. 80 kV with alternatively no added filtration and a cerium or samarium filter. Cerium has a K absorption edge at 40.4 keV, and samarium at 46.8 keV, and both materials generate a hardened beam compared with the unfiltered spectrum.
- The DEXA technique typically involves an X-ray tube and scintillation detector mounted on a C-arm arrangement - see Figure 7.18 - so that the patient is exposed to a pencil X-ray beam scanning in a rectilinear fashion. The pencil beam is used to reduce the detection of scattered radiation and the scintillation detector typically consists of a CdWO4 or NaI(Tl) scintillator coupled to a photodetector. The filter assembly is used to switch filters and calibration standards into and out of the pencil beam at appropriate intervals. Scan times with this approach are of the order of 2 to 5 minutes, depending on the examination, which are reduced in second generation instruments where a fan-shaped X-ray beam and an array of detectors are used. By rotating the C-arm around the patient during the scan in the second generation devices, a CT image can be formed. The output of the scintillation detector is fed to a computer for dual-energy data processing and image display. A host of body composition parameters can be derived from the image data, e.g. bone mineral density and soft tissue composition.
- Note that patient doses in DEXA are trivial, even in comparison to chest radiography[56].
Image Superimposition
[edit | edit source]Correlative imaging is widely used in medical diagnosis so that information gleaned from a number of imaging modalities can be merged to form a bigger picture about a patient's condition. It is generally necessary to spatially align image data prior to the fusion process so as to address differences in orientation, magnification and other acquisition factors. This alignment process is generally referred to as image registration.
Image Registration
[edit | edit source]- Suppose we have two images to be registered - a planar nuclear medicine scan and a radiograph, as shown in Figure 7.19.
- The registration process generally assumes that a correspondence exists between spatial locations in the two images so that a Coordinate Transfer Function (CTF) can be established which can be used to map locations in one image to those of the other. In the above example, as in many clinical situations, a number of compatibility issues need to be addressed first. The obvious one arises from the different protocols used for image acquisitions, i.e. a palmar view in the bone scan and a posterior-anterior (PA) projection radiograph. We can handle this issue in our example case by extracting the right hand data from the bone scan and then mirroring it. A related issue arises when different digital resolutions are used - in this case, the nuclear medicine image was acquired using a 256 x 256 x 8-bit resolution, while the radiograph was acquired using a 2920 x 2920 pixel matrix with a 12-bit contrast resolution.

- When we assume minimal spatial distortion and identical positioning in the two images, we can infer a spatially uniform CTF, i.e. the transform applied to one pixel can also be applied to each and every other pixel. Let's call the two images to be registered A and B, with image A being the one to be processed geometrically to correspond as exactly as possible with image B. The CTF can then be represented by the following equations:
- and
- where:
- f and g define the transform in the horizontal and vertical image dimensions;
- (u,v) are the spatial co-ordinates in image A; and
- (x,y) are the spatial co-ordinates in image B.
- The first computing step is to generate an initially empty image C in the co-ordinate frame (x,y) and fill it with pixel values derived from applying the CTF to image A. The resultant image we can say is a version of image A registered to image B.
- The question, of course, is how to determine the CTF. For situations where simple geometric translations and rotations in the x- and y-dimensions are required, the functions f and g can involve relatively straight-forward bilinear interpolations. Such transformations can also compensate for image magnification effects, and the resultant processes are referred to as rigid transforms. When spatial non-uniformities are encountered, non-rigid transforms can be used to apply different magnification factors in both x- and y-dimensions, as well as other geometric translations - in which case higher order interpolants can be applied.

- Determination of the parameters of the CTF is needed and there are numerous methods we can use, for example:
- Landmarks - where corresponding locations of prominent anatomical features in both images can be identified and two sets of co-ordinates can be derived on this basis to define the CTF. Note that artificial landmarks can be created using external markers during image acquisition, where, for instance, a set of markers which are both radioactive and radio-opaque can be mounted during image acquisitions.
- Function Minimization/Maximization - where an indicator of the quality of registration is monitored as various geometric transformations are applied to the image in an iterative fashion to search for a set of parameters which minimize (or maximise) this indicator. Statistically-based computations such as Mutual Information (MI) maximisation can be used for this purpose. A major advantage is that type of image registration can be achieved automatically without operator input. An iterative process is generally followed, where the MI indicator is maximized initially for low resolution versions of the two images and then progressively for increasingly higher resolutions. Note however that reducing the resolution of the radiograph can substantially effect its spatial quality and that, while registration may be effected at this lower resolution, the resultant CTF can be used with appropriate magnification to register the bone scan with the full resolution radiograph - as illustrated in Figure 7.20.
Image Fusion
[edit | edit source]- A method of combining image data to form a fusion display is required once images have been registered. A simple approach is to add the two images. Multiplying them is also an option. However, this form of image fusion tends to obscure the underlying anatomy when hot spots exist in the nuclear medicine data. A more effective approach is to use an image compositing technique called Alpha Blending, which uses a transparency value, α, to determine a proportional mixing of the two images, as illustrated in Figure 7.21.

- This type of approach is highly developed in the publishing industry and a wide range of fusion options are available. A common one, which was used for the images above, is to apply an equation of the form:
- A transparency value of 0.5 was used to generate the image in the left panel of Figure 7.21, for instance, with the result that the underlying anatomy can be discerned through the hot spot. A powerful feature of this approach is that the fusion transparency can be varied interactively so as to optimize the data presentation, for instance, or to confirm the quality of the registration process.
- This blending approach can be extended to incorporate a variable opacity function, where different transparency values are applied to different parts of the grey scale of one image. Note that the terms transparency and opacity have a reciprocal relationship in this context. Example blends are shown in the following figure.
- The High-Low-High opacity function, for instance, applies a high level of opacity to pixel values at the top and bottom ends of the contrast scale of one of the images and a low opacity to intermediate pixel values. The result is improved visualization of fused data outside of hot spot regions - as illustrated in the top right panel of Figure 7.21. The Low-High-Low function has the opposite effect and generates the capability to visualize the relevant anatomical detail with a highlighted region around it - as shown in the bottom left panel of the figure. Logarithmic, exponential and other opacity functions can also be applied, depending on the nature of the two images to be fused.
References
[edit | edit source]- ↑ Hamers S, Freyschmidt J & Neitzel U, 2001. Digital radiography with a large-scale electronic flat-panel detector vs. screen-film radiography: Observer preference in clinical skeletal diagnostics. Eur Radiol, 11:1753-9.
- ↑ Peer S, Neitzel U, Giacomuzzi SM, Pechlaner S, Künzel KH, Peer R, Gassner E, Steingruber I, Gaber O & Jaschke W, 2002. Direct digital radiography versus storage phosphor radiography in the detection of wrist fractures. Clin Radiol, 57:258-62.
- ↑ Uffmann M, Schaefer-Prokop C, Neitzel U, Weber M, Herold CJ & Prokop M, 2004. Skeletal applications for flat-panel versus storage-phosphor radiography: Effect of exposure on detection of low-contrast details. Radiology, 231:506-14.
- ↑ Hamer OW, Völk M, Zorger N, Borisch I, Büttner R, Feuerbach S & Strotzer M, 2004. Contrast-detail phantom study for x- ray spectrum optimization regarding chest radiography using a cesium iodide-amorphous silicon flat-panel detector. Invest Radiol, 39:610-8.
- ↑ Uffmann M, Neitzel U, Prokop M, Kabalan N, Weber M, Herold CJ & Schaefer-Prokop C, 2004. Flat-panel-detector chest radiography: Effect of tube voltage on image quality. Radiology, 235:642-50.
- ↑ Hamer OW, Sirlin CB, Strotzer M, Borisch I, Zorger N, Feuerbach S & Völk M, 2005. Chest radiography with a flat-panel detector: Image quality with dose reduction after copper filtration. Radiology, 237:691-700.
- ↑ Bacher K, Smeets P, Bonnarens K, De Hauwere A & Verstraete K, Thierens H, 2003. Dose reduction in patients undergoing chest imaging: Digital amorphous silicon flat-panel detector radiography versus conventional film-screen radiography and phosphor-based computed radiography. Am J Roentgenol, 181:923-9
- ↑ Völk M, Hamer OW, Feuerbach S & Strotzer M, 2004. Dose reduction in skeletal and chest radiography using a large-area flat- panel detector based on amorphous silicon and thallium-doped cesium iodide: Technical background, basic image quality parameters, and review of the literature. Eur Radiol, 14:827-34.
- ↑ Bacher K, Smeets P, Ver- eecken L, De Hauwere A, Duyck P, De Man R, Verstraete K & Thierens H, 2006. Image quality and radiation dose on digital chest imaging: Comparison of amorphous silicon and amorphous selenium flat-panel systems. Am J Roentgenol, 187:630-7.
- ↑ Davies AG, Cowen AR, Kengyelics SM, Moore J & Sivananthan MU, 2007. Do flat detector cardiac X-ray systems convey advantages over image-intensifier-based systems? Study comparing X-ray dose and image quality. Eur Radiol, 17:1787-94.
- ↑ Stadlbauer A, Salomonowitz E, Radlbauer R, Salomonowitz G & Lomoschitz F, 2010. A SWOT (Strengths, Weaknesses, Opportunities and Threats) analysis of current digital radiography systems for thorax- and skeletal diagnostics. Gesundheitsökonomie & Qualitätsmanagement, 15:199-207.
- ↑ Schaefer-Prokop C, Neitzel U, Venema HW, Uffmann M & Prokop M, 2008. Digital chest radiography: An update on modern technology, dose containment and control of image quality. Eur Radiol, 18:1818-30.
- ↑ Schaefer-Prokop CM, De Boo DW, Uffmann M & Prokop M, 2009. DR and CR: Recent advances in technology. Eur J Radiol, 72:194-201.
- ↑ Veldkamp WJ, Kroft LJ & Geleijns J, 2009. Dose and perceived image quality in chest radiography. Eur J Radiol. 2009 Nov;72(2):209-17.
- ↑ McAdams HP, Samei E, Dobbins J 3rd, Tourassi GD & Ravin CE, 2006. Recent advances in chest radiography. Radiology. 2006 Dec;241(3):663-83.
- ↑ Johns PC & Yaffe MJ, 1987. X-ray characterisation of normal and neoplastic breast tissues. Phys Med Biol, 32:675-95.
- ↑ Rivetti S, Canossi B, Battista R, Lanconelli N, Vetruccio E, Danielli C, Borasi G & Torricelli P, 2009. Physical and clinical comparison between a screen-film system and a dual-side reading mammography-dedicated computed radiography system. Acta Radiol, 50:1109-18.
- ↑ Liu X, Shaw CC, Lai CJ, Wang T, 2011. Comparison of scatter rejection and low-contrast performance of scan equalization digital radiography (SEDR), slot-scan digital radiography, and full-field digital radiography systems for chest phantom imaging. Med Phys, 38:23-33.
- ↑ Lazzari B, Belli G, Gori C & Rosselli Del Turco M, 2007. Physical characteristics of five clinical systems for digital mammography. Med Phys. 2007 Jul;34(7):2730-43.
- ↑ Reiser I & Sechopoulos I, 2014. A review of digital breast tomosynthesis. Medical Physics International, 2:57-66.
- ↑ Gennaro G, Toledano A, di Maggio C, Baldan E, Bezzon E, La Grassa M, Pescarini L, Polico I, Proietti A, Toffoli A & Muzzio PC, 2010. Digital breast tomosynthesis versus digital mammography: A clinical performance study. Eur Radiol, 20:1545-53.
- ↑ Sprawls P, 2019. The scientific and technological developments in mammography: A continuing quest for visibility. Medical Physics International, 7:141-66.
- ↑ Gennaro G, Golinelli P, Bellan E, Colombo P, D'Ercole L, Di Nallo A, Gallo L, Giordano C, Meliadò G, Morri B, Nassivera E, Oberhofer N, Origgi D, Paolucci M, Paruccini N, Piergentili M, Rizzi E & Rossi R, 2008. Automatic Exposure Control in Digital Mammography: Contrast-to-Noise Ratio Versus Average Glandular Dose. Lecture Notes in Computer Science, 5116: 711-5.
- ↑ Yaffe MJ & Mainprize JG, 2011. Risk of radiation-induced breast cancer from mammographic screening. Radiology, 258:98-105.
- ↑ Niklason LT, Sorenson JA & Nelson JA, 1981. Scattered radiation in chest radiography, Med Phys, 8:677-681.
- ↑ Siewerdsen JH, Daly MJ, Bakhtiar B, Moseley DJ, Richard S, Keller H & Jaffray DA, 2006. A simple, direct method for x-ray scatter estimation and correction in digital radiography and cone-beam CT. Med Phys, 33:187-97.
- ↑ Nelson JA, Miller FJ Jr, Kruger RA, Liu PY & Bateman W, 1982. Digital subtraction angiography using a temporal bandpass filter: Initial clinical results. Radiology, 145:309-13.
- ↑ Jurriaans E & Wells IP, 1993. Bolus chasing: A new technique in peripheral arteriography. Clin Radiol, 48:182-5.
- ↑ Bosanac Z, Miller RJ & Jain M, 1998. Rotational digital subtraction carotid angiography: Technique and comparison with static digital subtraction angiography. Clin Radiol, 53:682-7.
- ↑ Anxionnat R, Bracard S, Macho J, Da Costa E, Vaillant R, Launay L, Trousset Y, Romeas R & Picard L, 1998. 3D angiography. Clinical interest. First applications in interventional neuroradiology. J Neuroradiol, 25:251-62.
- ↑ Kalender WA, 2006. X-ray computed tomography. Phys Med Biol, 51:R29-43.
- ↑ Kalender WA & Kyriakou Y, 2007. Flat-detector computed tomography (FD-CT). Eur Radiol, 17:2767-79.
- ↑ Kyriakou Y & Kalender WA, 2007. X-ray scatter data for flat-panel detector CT. Phys Med, 23:3-15.
- ↑ Tang X, Hsieh J, Nilsen RA, Dutta S, Samsonov D & Hagiwara A. A three-dimensional-weighted cone beam filtered backprojection (CB-FBP) algorithm for image reconstruction in volumetric CT-helical scanning. Phys Med Biol, 51:855-74.
- ↑ Scarfe WC & Farman AG, 2008. What is cone-beam CT and how does it work? Dent Clin North Am, 52:707-30.
- ↑ König M, 2003. Brain perfusion CT in acute stroke: Current status. Eur J Radiol, 45 Suppl 1:S11-22.
- ↑ Adams JE, 2009. Quantitative computed tomography. Eur J Radiol, 71:415-24.
- ↑ Hu H, 1999. Multi-slice helical CT: Scan and reconstruction. Med Phys, 26:5-18.
- ↑ Flohr TG, Schaller S, Stierstorfer K, Bruder H, Ohnesorge BM & Schoepf UJ, 2005. Multi-detector row CT systems and image-reconstruction techniques. Radiology, 235:756-73.
- ↑ Schardt P, Deuringer J, Freudenberger J, Hell E, Knüpfer W, Mattern D & Schild M, 2004. New x-ray tube performance in computed tomography by introducing the rotating envelope tube technology. Med Phys, 31:2699-706.
- ↑ Bardo DM & Brown P, 2008. Cardiac multidetector computed tomography: Basic physics of image acquisition and clinical applications. Curr Cardiol Rev, 4:231-43.
- ↑ Halliburton SS, 2009. Recent technologic advances in multi-detector row cardiac CT. Cardiol Clin, 27:655-64.
- ↑ Flohr TG, Bruder H, Stierstorfer K, Petersilka M, Schmidt B & McCollough CH, 2008. Image reconstruction and image quality evaluation for a dual source CT scanner. Med Phys, 35:5882-97.
- ↑ Kalender WA & Quick HH, 2011. Recent advances in medical physics. Eur Radiol, 21:501-4.
- ↑ Kim GR, Hur J, Lee SM, Lee HJ, Hong YJ, Nam JE, Kim HS, Kim YJ, Choi BW, Kim TH & Choe KO, 2011. CT fluoroscopy-guided lung biopsy versus conventional CT-guided lung biopsy: A prospective controlled study to assess radiation doses and diagnostic performance. Eur Radiol, 21:232-9.
- ↑ Hohl C, Suess C, Wildberger JE, Honnef D, Das M, Mühlenbruch G, Schaller A, Günther RW & Mahnken AH, 2008. Dose reduction during CT fluoroscopy: Phantom study of angular beam modulation. Radiology, 246:519-25.
- ↑ Hara AK, Paden RG, Silva AC, Kujak JL, Lawder HJ & Pavlicek W, 2009. Iterative reconstruction technique for reducing body radiation dose at CT: Feasibility study. Am J Roentgenol, 193:764-71.
- ↑ Sagara Y, Hara AK, Pavlicek W, Silva AC, Paden RG & Wu Q, 2010. Abdominal CT: Comparison of low-dose CT with adaptive statistical iterative reconstruction and routine-dose CT with filtered back projection in 53 patients. Am J Roentgenol, 195:713-9.
- ↑ Löve A, Olsson ML, Siemund R, Stålhammar F, Björkman-Burtscher IM and Söderberg M, 2013. Six iterative reconstruction algorithms in brain CT: a phantom study on image quality at different radiation dose levels. Br J Radiol 86:20130388.
- ↑ Stiller W, 2018. Basics of iterative reconstruction methods in computed tomography: A vendor-independent overview. Eur J Radiol 109:147-154
- ↑ Fleischmann D & Boas FE, 2011. Computed tomography - Old ideas and new technology. Eur Radiol, 21:510-7.
- ↑ Karcaaltincaba M & Aktas A, 2010. Dual-energy CT revisited with multidetector CT: Review of principles and clinical applications. Diagn Interv Radiol, doi: 10.4261/1305-3825.DIR.3860-10.0, Epub ahead of print.
- ↑ Boll DT, Patil NA, Paulson EK, Merkle EM, Simmons WN, Pierre SA & Preminger GM, 2009. Renal stone assessment with dual-energy multidetector CT and advanced postprocessing techniques: Improved characterization of renal stone composition - Pilot study. Radiology, 250:813-20.
- ↑ Remy-Jardin M, Faivre JB, Pontana F, Hachulla AL, Tacelli N, Santangelo T & Remy J, 2010. Thoracic applications of dual energy. Radiol Clin North Am, 48:193-205.
- ↑ Goo HW & Goo JM, 2017. Dual-Energy CT: New Horizon in Medical Imaging.. Korean J Radiol, 18(4):555-569
- ↑ Mettler FA Jr, Huda W, Yoshizumi TT & Mahesh M, 2008. Effective doses in radiology and diagnostic nuclear medicine: A catalog. Radiology, 248:254-63.



















