A-level Physics (Advancing Physics)/Print Version
| This is the print version of A-level Physics (Advancing Physics) You won't see this message or any elements not part of the book's content when you print or preview this page. |
Welcome to the Wikibooks textbook on Physics, designed to contain everything you need to know for the OCR Physics B (Advancing Physics) specification [1]. All sorts of useful documents for this specification are available at http://www.ocr.org.uk/qualifications/as_alevelgce/physics_b_advancing_physics/documents.html .
All units are assumed to be
The_SI_System_of_Units
SI units are used throughout science in many countries of the world. It was adopted in 1960 as the preferred variant of the metric system. The metric system itself dates back to the 1790.
Base units
There are seven base units, from which all other units are derived. Every other unit is either a combination of two or more base units, or a reciprocal of a base unit. Since 2019 all of the base units are defined with reference to measurable natural phenomena. Also, notice that the kilogram is the only base unit with a prefix. This is because the gram is too small for most practical applications.
| Quantity | Name | Symbol |
|---|---|---|
| Length | metre | m |
| Mass | kilogram | kg |
| Time | second | s |
| Electric Current | ampere | A |
| Thermodynamic Temperature | kelvin | K |
| Amount of Substance | mole | mol |
| Luminous Intensity | candela | cd |
Derived units
Most of the derived units are the base units divided or multiplied together. Some of them have special names. You can see how each unit relates to any other unit, and knowing the base units for a particular derived unit is useful when checking if your working is correct.
Note that "m/s", "m s-1", "m·s-1" and are all equivalent. The negative exponent form is generally preferred, for example "kg·m-1·s-2" is unambiguous. In contrast "kg/m/s2" is ambiguous -
is it or is it ?
| Quantity | Name | Symbol | In terms of other derived units | In terms of base units |
|---|---|---|---|---|
| plane angle | radian | rad | m m-1 = 1 | |
| solid angle | steradian | sr | m2 m-2 = 1 | |
| Area | square metre | m2 | m2 | |
| Volume | cubic metre | m3 | m3 | |
| Speed/Velocity | metre per second | m s-1 | m s-1 | |
| Acceleration | metre per second squared | m s-2 | m s-2 | |
| Density | kilogram per cubic metre | kg m-3 | m-3 kg | |
| Specific Volume | cubic metre per kilogram | m3 kg-1 | m3 kg-1 | |
| Current Density | ampere per square metre | A m-2 | m-2 A | |
| Magnetic Field Strength | ampere per metre | m-1 A | m-1 A | |
| Concentration | mole per cubic metre | m-3 mol | m-3 mol | |
| Frequency | hertz | Hz | s-1 | s-1 |
| Force | newton | N | kg m s-2 | m kg s-2 |
| Pressure Stress |
pascal | Pa | N m-2 | m-1 kg s-2 |
| Energy Work/ Quantity of Heat |
joule | J | N m | m2 kg s-2 |
| Power Radiant Flux |
watt | W | J s-1 | m2 kg s-3 |
| Electric Charge Quantity of Electricity |
coulomb | C | A s | s A |
| Electric Potential Potential Difference Electromotive Force |
volt | V | W A-1 | m2 kg s-3 A-1 |
| Capacitance | Farad | F | C V-1 | m-2 kg-1 s4 A2 |
| Electric Resistance | Ohm | Ω | V A-1 | m2 kg s-3 A-2 |
| Electric Conductance | siemens | S | A V-1 Ω-1 |
m-2 kg-1 s3 A2 |
| Magnetic Flux | weber | Wb | V s | m2 kg s-2 A-1 |
| Magnetic Flux Density | Tesla | T | Wb m-2 | kg s-2 A-1 |
| Inductance | henry | H | Wb A-1 | m2 kg s-2 A-2 |
| Celsius Temperature | degree Celsius | °C | K - 273.15 | |
| Luminous Flux | lumen | lm | sr cd | |
| Illuminance | lux | lx | lm m-2 | sr m-2 cd |
| Activity of a Radionuclide | bequerel | Bq | s-1 | s-1 |
| Absorbed dose | gray | Gy | J kg-1 | m2 s-2 |
| Dose equivalent | sievert | Sv | J kg-1 | m2 s-2 |
Symbols usually start with a lower case letter unless the unit was named after somebody - for example "newtons" (note lower case letter when writing in English about the units) were named after Sir Isaac Newton, "watts" after James Watt, "farads" after Michael Faraday and so on.
Prefixes
The SI units can have prefixes to make larger or smaller numbers more manageable. For example, visible light has a wavelength of roughly 0.0000005 m, but it is more commonly written as 500 nm. If you must specify a quantity like this in metres, you should write it in standard form. As given by the table below, 1 nm = 1×10-9 m. In standard form, the first number must be between 1 and 10. So to put 500 nm in standard form, you would divide the 500 by 100 to get 5, then multiply the factor by 100 (so that it's still the same number), getting 5×10-7 m. The power of 10 in this answer, i.e.,. -7, is called the exponent, or the order of magnitude of the quantity.
| Prefix | Symbol | Factor | Common Term |
|---|---|---|---|
| peta | P | quadrillions | |
| tera | T | trillions | |
| giga | G | billions | |
| mega | M | millions | |
| kilo | k | thousands | |
| hecto | h | hundreds | |
| deca | da | tens | |
| deci | d | tenths | |
| centi | c | hundredths | |
| milli | m | thousandths | |
| micro | µ | millionths | |
| nano | n | billionths | |
| pico | p | trillionths | |
| femto | f | quadrillionths |
Homogenous equations
Equations must always have the same units on both sides, and if they don't, you have probably made a mistake. Once you have your answer, you can check that the units are correct by doing the equation again with only the units.
Example 1
For example, to find the velocity of a cyclist who moved 100 metres in 20 seconds, you have to use the formula
so your answer would be 100÷20 = 5 m·s-1.
This question has the units m ÷ s and should give an answer in m·s-1. Here, the equation was correct, and makes sense. In this case a middle-dot (·) has been inserted between the "m" and the "s" to show that this is metres per second, not milliseconds.
Often, however, it isn't that simple. If a car of mass 500 kg had an acceleration of 0.2 m·s-2, you could use Newton's second law
to show that the force provided by the engines is 100 N. At first glance it would seem the equation is not homogeneous, since the equation uses the units (kg) × (m·s-2), which should give an answer in kg·m·s-2. If you look at the derived units table above, you can see that a newton is in fact equal to kg·m·s-2, and therefore the equation is correct.
Example 2
Using the same example as above, imagine that we are only given the mass of the car and the force exerted by the engine, and have been asked to find the acceleration of the car. Using
again, we need to rearrange it for a. We do this incorrectly by setting
- .
By inserting the numbers, we get the answer a = 5 m·s-2. We already know that this is wrong from the example above, but by looking at the units, we can see why this is the case
- .
The units are m-1·s2, when we were looking for m·s-2. The problem is the fact that "F=ma" was rearranged incorrectly. The correct formula was
- ,
and using it will give the correct answer of 0.2 m·s-2. The units for the correct formula are
- .
, unless stated otherwise. Diagrams can be enlarged by clicking on them.
Chapters are probably marked as 75% complete () because they are complete, but the author is not entirely happy with the correctness of the contents. Please look at these and check them!
AS Exams
=
Physics in Action
=
Lenses
Curvature of Wavefronts
Light can be viewed as beams travelling between points. However, from most light sources, the light radiates outwards as a series of wavefronts or ripples. Light from a light source is bent - wavefronts or ripples of light have a property known as curvature.

As light travels further away from its source, its curvature decreases. Consider a sphere expanding gradually from a point, which represents a given wavefront of light. As the sphere expands, the curvature of its surface decreases when we look at any part of the surface with a constant area. It should be noted at this point that light from a source infinitely far away has 0 curvature - it is straight. This is useful, as ambient light (light from a source that is far away) can be assumed to have a curvature of 0, as the difference between this and its actual curvature is negligible.
The curvature of a wavefront is given as:
,
where v is the distance from the wavefront to the in-focus image depicted by the light. Curvature is measured in dioptres (D).
Power of lenses

The function of a lens is to increase or decrease the curvature of a wavefront. Lenses have a 'power'. This is the curvature which the lens adds to the wavefront. Power is measured in dioptres, D, and is given by the formula:
,
where f equals the focal length of the lens, in meters. This is the distance between the lens and the point where an image will be in focus, if the wavefronts entering the other side of the lens are parallel.
The Lens Equation

Overall, then, the formula relating the curvature of the wavefronts leaving a lens to the curvature of the wavefronts entering it is:
where v is the distance between the lens (its centre) and the in-focus image formed, u is the distance between the lens (its centre) and the object which the in-focus image is of, and f is the focal length of the lens. The power of the lens can be substituted in for the reciprocal of f, as they are the same thing.
The Cartesian Convention
If we were to place a diagram of the lens on a grid, labelled with cartesian co-ordinates, we would discover that measuring the distance of the object distance is negative, in comparison to the image distance. As a result, the value for u must always be negative. This is known as the Cartesian convention.
This means that, if light enters the lens with a positive curvature, it will leave with a negative curvature unless the lens is powerful enough to make the light leave with a positive curvature.
Types of Lens

There are two types of lens:
Converging lenses add curvature to the wavefronts, causing them to converge more. These have a positive power, and have a curved surface which is wider in the middle than at the rim.
Diverging lenses remove curvature from the wavefronts, causing them to diverge more. These have a negative power, and have a curved surface with a dip in the middle.
Magnification
Magnification is a measure of how much an image has been enlarged by a lens. It is given by the formula:
where h1 and h2 are the heights of the image (or object) before and after being magnified, respectively. If an image is shrunk by a lens, the magnification is between 0 and 1.
Magnification can also be given as:
where v and u are the image and object distances. Therefore:
An easy way to remember this in the middle of an exam is the formula:
where I is image size, A is actual size of the object M is the magnification factor.
Questions
1. Light reflected off a cactus 1.5m from a 20D lens forms an image. How many metres is it from the other side of the lens?
3. A lens in an RGB projector causes an image to focus on a large screen. What sort of lens is it? Is its power positive or negative?
4. What is the focal length of a 100D lens?
5. The film in a camera is 5mm from a lens when automatically focussed on someone's face, 10m from the camera. What is the power of the lens?
6. The light from a candle is enlarged by a factor of 0.5 by a lens, and produces an image of a candle, 0.05m high, on a wall. What is the height of the candle?
Refraction
Reflection

Reflection is when light 'bounces' off a material which is different to the one in which it is travelling. You may remember from GCSE (or equivalent) level that we can calculate the direction the light will take if we consider a line known as the 'normal'. The normal is perpendicular to the boundary between the two materials, at the point at which the light is reflected. The angle between the normal and the ray of light is known as the angle of reflection (r). The ray of light will be reflected back at the same angle as it arrived at the normal, on the other side of the normal.
Refraction
Refraction is when light changes velocity when it travels across the boundary between two materials. This causes it to change direction. The angle between the normal and the refracted ray of light is known as the angle of refraction (r).
The Refractive Index
The refractive index is a measure of how much light will be refracted on the boundary between a material and a 'reference material'. This reference material is usually either air or a vacuum. It is given by the following formula:
where c0 is the speed of light in a vacuum (3 x 108 m/s) and c1 is the speed of light in the material.
Snell's Law
We can relate the refractive index to the angles of incidence (i) and refraction (r) using the following formula, known as Snell's Law:
Total Internal Reflection
Normally, when light passes through a non-opaque material, it is both reflected and refracted. However, sometimes, rays of light are totally internally reflected; in other words, they are not refracted, so no light goes outside the material. This is useful in optic fibres, which allow a signal to be transmitted long distances at the speed of light because the light is totally internally reflected.
Critical Angle
The critical angle is the minimum angle of incidence, for a given material, at which rays of light are totally internally reflected. At the critical angle (C), the angle of refraction is 90°, as any smaller angle of incidence will result in refraction. Therefore:
Since sin 90° = 1:
In word form, in a material with refractive index n, light will be totally internally reflected at angles greater than the inverse sine of the reciprocal of the refractive index.
Questions
1. A ray of light is reflected from a mirror. Its angle to the normal when it reaches the mirror is 70°. What is its angle of reflection?
2. The speed of light in diamond is 1.24 x 108 m/s. What is its refractive index?
3. The refractive index of ice is 1.31. What is the speed of light in ice?
4. A ray of light passes the boundary between air and a transparent material. The angle of refraction is 20°, and the angle of incidence is 10°. What is the speed of light in this material? Why is it impossible for this material to exist?
5. What is the critical angle of a beam of light leaving a transparent material with a refractive index of 2?
See also
Digital Storage
Digital Data
There are two different types of data: analogue and digital. Analogue data can, potentially, take on any value. Examples include a page of handwritten text, a cassette, or a painting. Digital data can only take on a set range of values. This enables it to be processed by a computer. Examples include all files stored on computers, CDs, DVDs, etc.
Pixels

Digital images are made up of pixels. A pixel represents the value of an individual square of the image, and it has a value assigned to it. The total number of pixels in an image is just like the formula for the area of a rectangle: number of pixels across multiplied by number of pixels down. When representing text, each pixel is a component of one character (for example, a letter, a number, a space, or a new line), it is not the entirety of a character. For instance if the letter 'E' was to be taken as an example and a section was to be taken through the three protrusions; a minimum of seven (7) pixels would be used, one white pixel at the top, then one black (for the first protrusion), then one white for the gap, then a black one for the centre - and so on. A type face - such as Helvetica, or Times New Roman, maybe made up of a more complex pattern of pixels to allow for serif details.
Bits
Each pixel's value is digital: it takes on a definite value. In a higher quality image, each pixel can take on a greater variety of values. Each pixel's value is encoded as a number of bits. A bit is a datum with a value of either 0 or 1. The more values a pixel can take on, the more bits must be used to represent its value. The number of values (N) that a pixel represented by I bits can take on is given by the formula:
N = 2I
Hence:
Log base 10 used here. For ratios, the base of the log does not matter, now we have evaluated log 2 using base 10 log N must be base 10 as well.
A pixel may be represented by values for red, green and blue, in which case each colour channel will have to be encoded separately. When dealing with text, the number of values is equal to the number of possible characters.
Overall, for an image:
Amount of information in an image (bits) = number of pixels x bits per pixel.
Bytes
A byte is equal to 8 bits. The major difference between bytes and SI units is that when prefixes (such as kilo-, mega-, etc.) are attached, we do not multiply by 103 as the prefix increases. Instead, we multiply by 1024. So, 1 kilobyte = 1024 bytes, 1 megabyte = 10242 bytes, 1 gigabyte = 10243 bytes, and 1 terabyte = 10244 bytes.
Questions
1. An image transmitted down a SVGA video cable is 800 pixels wide, and 600 pixels high. How many pixels are there in the image?
2. A grayscale image is encoded using 3 bits. How many possible values can each pixel have?
3. The characters in a text document are numbered from 0 - 255. How many bits should each character be encoded with?
4. A page contains 30 lines of text, with an average of 15 characters on each line. Each character is represented by 4 bits. How many megabytes of uncompressed storage will a book consisting of 650 pages like this fill on a computer's hard disk?
5. A 10 cm wide square image is scanned into a computer. Each pixel is encoded using 3 channels (red, green and blue), and each channel can take on 256 possible values. One pixel is 0.01 mm wide. How much information does the scanned image contain? Express your answer using an appropriate unit.
Digital Processing
As we have already seen, a digital image consists of pixels, with each pixel having a value which represents its colour. For the purposes of understanding how digital images are manipulated, we are going to consider an 8-bit grayscale image, with pixel values ranging from 0 to 255, giving us 256 (28) levels of grey. 0 represents white, and 255 represents black. This is the image we are going to consider:
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 050 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 235 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 205 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 255 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 095 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 185 | 000 | 150 | 150 | 150 | 150 | 150 |
The image consists of an edge, and some random noise. There are two methods of smoothing this image (i.e. removing noise) that you need to know about:
Mean Smoothing
In order to attempt to remove noise, we can take the mean average of all the pixels surrounding each pixel (and the pixel itself) as the value of the pixel in the smoothed image, as follows:
| 000 | 000 | 000 | 000 | 050 | 100 | 150 | 133 | 133 | 133 |
| 000 | 026 | 026 | 026 | 050 | 100 | 150 | 139 | 139 | 139 |
| 000 | 026 | 026 | 026 | 050 | 106 | 173 | 173 | 150 | 150 |
| 000 | 026 | 026 | 026 | 050 | 106 | 173 | 173 | 150 | 150 |
| 000 | 000 | 000 | 000 | 050 | 106 | 173 | 173 | 150 | 150 |
| 043 | 028 | 000 | 000 | 050 | 100 | 150 | 150 | 150 | 150 |
| 043 | 028 | 000 | 000 | 050 | 100 | 150 | 150 | 150 | 150 |
| 043 | 028 | 000 | 000 | 050 | 100 | 150 | 150 | 144 | 141 |
| 000 | 000 | 000 | 000 | 050 | 100 | 150 | 150 | 144 | 141 |
| 000 | 000 | 021 | 021 | 071 | 100 | 150 | 150 | 144 | 141 |
| 000 | 000 | 31 | 31 | 081 | 100 | 150 | 150 | 150 | 150 |
This does remove the noise, but it blurs the image with means crucial anomalies and points may be missed.
Median Smoothing
A far better method is, instead of taking the mean, to take the median, as follows:
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
| 000 | 000 | 000 | 000 | 000 | 150 | 150 | 150 | 150 | 150 |
For this image, this gives a perfect result. In more complicated images, however, data will still be lost, although, in general, less data will be lost by taking the median than by taking the mean.
Edge Detection
We can detect the positioning of edges in an image using the 'Laplace rule', or 'Laplace kernel'. For each pixel in the image, we multiply its value by 4, and then subtract the values of the pixels above and below it, and on either side of it. If the result is negative, we treat it as 0. So, taking the median-smoothed image above, edge detection gives the following result:
| 000 | 000 | 000 | 000 | 000 | 150 | 000 | 000 | 000 | 000 |
| 000 | 000 | 000 | 000 | 000 | 150 | 000 | 000 | 000 | 000 |
| 000 | 000 | 000 | 000 | 000 | 150 | 000 | 000 | 000 | 000 |
| 000 | 000 | 000 | 000 | 000 | 150 | 000 | 000 | 000 | 000 |
| 000 | 000 | 000 | 000 | 000 | 150 | 000 | 000 | 000 | 000 |
| 000 | 000 | 000 | 000 | 000 | 150 | 000 | 000 | 000 | 000 |
| 000 | 000 | 000 | 000 | 000 | 150 | 000 | 000 | 000 | 000 |
| 000 | 000 | 000 | 000 | 000 | 150 | 000 | 000 | 000 | 000 |
| 000 | 000 | 000 | 000 | 000 | 150 | 000 | 000 | 000 | 000 |
| 000 | 000 | 000 | 000 | 000 | 150 | 000 | 000 | 000 | 000 |
Questions
1. How could the above methods be applied to a digital sound sample?
2. Which of the above methods would be suitable for smoothing sharp edges? Why?
3. Use median smoothing to remove noise from the following image of a white cat in a snowstorm (the black pixels have a value of 255):
| 000 | 255 | 000 | 000 |
| 000 | 000 | 000 | 255 |
| 255 | 000 | 000 | 000 |
| 000 | 000 | 255 | 000 |
4. Why would mean sampling not be appropriate for smoothing the image given in question 3?
5. Use mean smoothing to remove noise from the following image of a black cat in a coal cellar:
| 255 | 255 | 255 | 255 |
| 255 | 255 | 000 | 255 |
| 255 | 255 | 255 | 255 |
Digitisation
Digitisation of a signal is the process by which an analogue signal is converted to a digital signal.
Digitisation & Reconstruction
Let us consider the voltage output from a microphone. The signal which enters the microphone (sound) is an analogue signal - it can be any of a potentially infinite range of values, and may look something like this waveform (from an artificial (MIDI) piano):
When the microphone converts this signal to an electrical signal, it samples the signal a number of times, and transmits the level of the signal at that point. The following diagram shows sample times (vertical black lines) and the transmitted signal (the red line):
When we wish to listen to the sound, the digital signal has to be reconstructed. The gaps between the samples are filled in, but, as you can see, the reconstructed signal is not the same as the original sound:
Sampling Rate
The sampling rate when digitising an analogue signal is defined as the number of samples per. second, and is measured in Hertz (Hz), as it is a frequency. You can calculate the sampling rate using the formula:
The higher the sampling rate, the closer the reconstructed signal is to the original signal, but, unfortunately, we are limited by the bandwidth available. Theoretically, a sampling rate of twice the highest frequency of the original signal will result in a perfect reconstructed signal. In the example given above, the sampling rate is far too low, hence the loss of information.
Number of Levels
Another factor which may limit the quality of the reconstructed signal is the number of bits with which the signal is encoded. For example, if we use 3 bits per. sample, we only have 8 (23) levels, so, when sampling, we must take the nearest value represented by one of these levels. This leads to quantization errors - when a sample does not equal the value of the original signal at a given sample point.
Questions
1. Take samples for the signal below every 0.1ms, and then produce a reconstructed signal. How does it differ from the original?
2. A signal is sampled for 5 seconds at a sampling rate of 20 kHz. How many samples were taken?
3. Most sounds created by human speech except for 'ss' and 'ff' have a maximum frequency of 4 kHz. What is a suitable sampling rate for a low-quality telephone?
4. Using a sampling rate of 20 kHz and 3 bits, sample the following signal, and then produce a reconstructed signal. What is the maximum frequency that can be perfectly reconstructed using this sampling rate?
Signal Frequencies
The frequency of a wave describes how many waves go past a certain point in one second. Frequency is measured in Hertz (usually abbreviated Hz), and can be calculated using the formula:
V = fλ
where V is the velocity of the wave (in ms−1), f is the frequency of the wave (in Hz), and λ (the Greek letter lambda) is the wavelength of the wave (distance from one peak / trough to the next, in m).
Multiple Frequencies
Let us consider the following signal (time is in ms, and the y-axis represents volts):
This signal is constructed from a number of different sine waves, with different frequencies, added together. These sine waves are as follows:
Frequency Spectra
Each of these sine waves has a different frequency. You can see this, as they have different distances between their peaks and troughs. These frequencies can be plotted against the amplitude of the wave, as in the table, and chart drawn from it, below:
| Wave (y=) | Period (ms) | Amplitude (V) | Frequency (Hz) |
|---|---|---|---|
| 3sin x | 6.284 | 3 | 159 |
| sin(0.5x + 40) | 12.566 | 1 | 80 |
| 2sin(3x - 60) | 2.093 | 2 | 478 |
This chart is known as the frequency spectrum of a signal.
Fundamental Frequency
The fundamental frequency is the lowest frequency that makes up a signal. In the above example, the fundamental frequency is 80 Hz. It is always the frequency farthest to the left of a frequency spectrum, ignoring noise. Other frequencies are known as overtones, or harmonics.
Questions
1. What is the frequency of an X-ray (wavelength 0.5 nm)?
2. A sound wave, with a frequency of 44 kHz, has a wavelength of 7.7mm. What is the speed of sound?
3. What is the fundamental frequency of the following signal?
4. Approximately how many harmonics does it contain?
5. The three sine waves sin x°, 4sin(2x-50)° and 0.5sin(3x+120)° are added together to form a signal. What are the frequencies of each of the waves? What is the signal's fundamental frequency? Assume that the waves are travelling at the speed of light, and that 60° = 1mm.
Bandwidth
Bandwidth is the frequency of a signal. Although original signals have varying frequencies, when these are transmitted, for example, as FM radio waves, they are modulated so that they only use frequencies within a certain range. FM radio modulates the frequency of a wave, so it needs some variation in the frequencies to allow for transmission of multiple frequencies. Since bandwidth is a frequency, it is the number of bits per. second. The bandwidth required to transmit a signal accurately can be calculated by using 1 as the number of bits, giving the formula:
where B is bandwidth (in Hz), and t is the time taken to transmit 1 bit of data (in s).
The bandwidth of a signal regulates the bit rate of the signal, as, with a higher frequency, more information can be transmitted. This give us the formula (similar to the formula for lossless digital sampling):
b = 2B
where b is the bit rate (in bits per. second), and B is the bandwidth (in Hz).
Questions
1. A broadband internet connection has a bit rate of 8Mbit s−1 when downloading information. What is the minimum bandwidth required to carry this bit rate?
2. The same connection has a bandwidth of 100 kHz reserved for uploading information. What is the maximum bit rate that can be attained when uploading information using this connection?
3. A lighthouse uses a flashing light and Morse Code to communicate with a nearby shore. A 'dash' consists of the light being on for 2s. The light is left off for 1s between dots and dashes. What is the bandwidth of the connection?
4. The broadband connection in question two is used to upload a 1Mbyte image to a website. How long does it take to do this?
Charge
Electrons, like many other particles, have a charge. While some particles have a positive charge, electrons have a negative charge. The charge on an electron is equal to approximately -1.6 x 10−19 coulomb. The coulomb (commonly abbreviated C) is the SI unit of charge. One coulomb is defined as the electric charge carried by 1 ampere (amp) of current in 1 second. It is normal to ignore the negative nature of this charge when considering electricity.
If we have n particles with the same charge Qparticle, then the total charge Qtotal is given by:
Qtotal = n Qparticle
By a simple rearrangement:
Questions
1. How much charge do 1234 electrons carry?
2. How many electrons does it take to carry 5 C of charge?
3. The total charge on 1 mole of electrons (6 x 1023 particles) is equal to 1 Faraday of charge. How many coulombs of charge are equal to 1 Faraday?
4. The mass of a ball is 50 mg. It is supplied 5 C of charge. Will there be any change in the mass of the ball? If so, calculate the change of the mass.
Current
Current is the amount of charge (on particles such as electrons) flowing through part of an electric circuit per second. Current is measured in amperes (usually abbreviated A), where 1 ampere is 1 coulomb of charge per second. The formula for current is:
([The triangle (Greek letter delta) means change in the quantity])
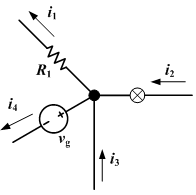
where I is current (in A), Q is charge (in C) and t is the time it took for the charge to flow (in seconds).
In a series circuit, the current is the same everywhere in the circuit, as the rate of flow of charged particles is constant throughout the circuit. In a parallel circuit, however, the current is split between the branches of the circuit, as the number of charged particles flowing cannot change. This is Kirchoff's First Law, stating that:
| “ | At any point in an electrical circuit where charge density is not changing in time [ie. there is no buildup of charge, as in a capacitor], the sum of currents flowing towards that point is equal to the sum of currents flowing away from that point. | ” |
In mathematical form:
(The character that resembles a sideways M is the Greek letter sigma, meaning 'sum of'.)
Questions

1. 10 coulombs flow past a point in a wire in 1 minute. How much current is flowing through the point?
2. How long does it take for a 2A current to carry 5C?
3. In the diagram on the left, I = 9A, and I1 = 4.5A. What is the current at I2?
4. What would I equal if I1 = 10A and I2 = 15A?
5. In the diagram on the left, in 5 seconds, 5C of charged particles flow past I1, and 6.7C flow past I2. How long does it take for 10C to flow past I?
Voltage
Charge moves through a circuit, losing potential energy as it goes. This means that the charge travels as an electric current. Voltage is defined as the difference in potential energy per. unit charge, i.e.
where V is voltage (in volts), E is the difference in potential energy (in joules) and Q is charge (in coulombs).
There are two electrical properties which are both measured in volts (commonly abbreviated V), and so both are known under the somewhat vague title of 'voltage'. Both are so called because they change the potential energy of the charge.
Electromotive Force (EMF)
Keep in mind, that EMF as the name suggests is not an electrical force, it is basically the potential difference across the terminals when the key is open i.e. when no current is drawn from the cell. EMF is named so by the scientists who performed faulty experiments and named it so, hence, just a tribute to their contribution to physics it is still called EMF but the definition has changed with time.
Potential Difference
As charge travels around a circuit, each coulomb of charge has less potential energy, so the voltage (relative to the power source) decreases. The difference between the electric potential at two points in a circuit is known as potential difference, and can be measured with a voltmeter.
Series Circuits
In a series circuit, the total voltage (EMF) is divided across the components, as each component causes the voltage to decrease, so each one has a potential difference. The sum of the potential differences across all the components is equal to the total voltage (but batteries have their own 'internal resistances', which complicates things slightly, as we will see).
Parallel Circuits
In a parallel circuit, the potential difference across each branch of the circuit is equal to the EMF, as the same 'force' is pushing along each path of the circuit. The number of charge carriers (current) differs, but the 'force' pushing them (voltage) does not.
Questions
1. A battery has an EMF of 5V. What is the total potential difference across all the components in the circuit?
2. The voltages (relative to the voltage of the battery) on either side of a resistor are -6V and -5V. What is the potential difference across the resistor?
3. At a given point in a circuit, 5C of charge have 10 kJ of potential energy. What is the voltage at this point?
4. Why do the electrons move to a point 1 cm further along the wire?
Power
Power is a measure of how much potential energy is dissipated (i.e. converted into heat, light and other forms of energy) by a component or circuit in one second. This is due to a drop in the potential energy, and so the voltage, of charge. Power is measured in Watts (commonly abbreviated W), where 1 W is 1 Js−1. It can be calculated by finding the product of the current flowing through a component / circuit and the potential difference across the component / circuit. This gives us the equation:
where P is the power dissipated (in W), E is the drop in potential energy (in Joules, J), t is the time taken (in s), I is the current (in A) and V is either potential difference or electromotive force (in V), depending on the component being measured.
Since power is the amount of energy changing form per. second, the amount of energy being given out each second will equal the power of the component giving out energy.
You should be able to substitute in values for I and V from other formulae (V=IR, Q=It) in order to relate power to resistance, conductance, charge and time, giving formulae like these:
Questions
1. The potential difference across a 9 W light bulb is 240 V. How much current is flowing through the light bulb?
2. How much energy is dissipated by a 10 W component in 1 hour?
3. The potential difference across a top-notch kettle, which can hold up to 1 litre of water, is 240 V, and the current is 12.5 A. 4.2 kJ of energy is required to raise the temperature of 1 kg of water by 1 °C. Assuming 100% efficiency and that the temperature has to be raised 80 °C (20 °C to 100 °C), how long does it take to boil 1 litre of water?
4. How much energy is dissipated by a 100Ω resistor in 10 seconds if 2A of current are flowing?
5. The charge on an electron is -1.6 x 10−19 C. How long does it take for a mole (6 x 1023 particles) of electrons to flow through a 40 W light bulb on a 240 V circuit?
Resistance and Conductance
Conductance is a measure of how well an artefact (such as an electrical component, not a material, such as iron) carries an electric current. Resistance is a measure of how well an artefact resists an electric current.
Resistance is measured in Ohms (usually abbreviated using the Greek letter Omega, Ω) and, in formulae, is represented by the letter R. Conductance is measured in Siemens (usually abbreviated S) and, in formulae, is represented by the letter G.
Resistance and conductance are each other's reciprocals, so:
and
Ohm's Law
Ohm's Law states that the potential difference across an artefact constructed from Ohmic conductors (i.e. conductors that obey Ohm's Law) is equal to the product of the current running through the component and the resistance of the component. As a formula:
V = IR
where V is potential difference (in V), I is current (in A) and R is resistance (in Ω).
In terms of Resistance
This formula can be rearranged to give a formula which can be used to calculate the resistance of an artefact:
In terms of Conductance
Since conductance is the reciprocal of resistance, we can deduce a formula for conductance (G):
The Relationship between Potential Difference and Current
From Ohm's Law, we can see that potential difference is directly proportional to current, provided resistance is constant. This is because two variables (let us call them x and y) are considered directly proportional to one another if:
where k is any positive constant. Since we are assuming that resistance is constant, R can equal k, so V=RI states that potential difference is directly proportional to current. As a result, if potential difference is plotted against current on a graph, it will give a straight line with a positive gradient which passes through the origin. The gradient will equal the resistance.
In Series Circuits
In a series circuit (for example, a row of resistors connected to each other), the resistances of the resistors add up to give the total resistance. Since conductance is the reciprocal of resistance, the reciprocals of the conductances add up to give the reciprocal of the total conductance. So:
In Parallel Circuits
In a parallel circuit, the conductances of the components on each branch add up to give the total conductance. Similar to series circuits, the reciprocals of the total resistances of each branch add up to give the reciprocal of the total resistance of the circuit. So:
When considering circuits which are a combination of series and parallel circuits, consider each branch as a separate component, and work out its total resistance or conductance before finishing the process as normal.
Questions
1. The potential difference across a resistor is 4V, and the current is 10A. What is the resistance of the resistor?
2. What is the conductance of this resistor?
3. A conductor has a conductance of 2S, and the potential difference across it is 0.5V. How much current is flowing through it?
4. A graph is drawn of potential difference across an Ohmic conductor, and current. For every 3 cm across, the graph rises by 2 cm. What is the conductance of the conductor?
5. On another graph of potential difference and current, the graph curves so that the gradient increases as current increases. What can you say about the resistor?
6. 3 resistors, wired in series, have resistances of 1kΩ, 5kΩ and 500Ω each. What is the total resistance across all three resistors?
7. 2 conductors, wired in parallel, have conductances of 10S and 5S. What is the total resistance of both branches of the parallel circuit?
8. The circuit above is attached in series to 1 10Ω resistor. What is the total conductance of the circuit now?
Internal Resistance
Batteries, just like other components in an electric circuit, have a resistance. This resistance is known as internal resistance. This means that applying Ohm's law (V = IR) to circuits is more complex than simply feeding the correct values for V, I or R into the formula.
The existence of internal resistance is indicated by measuring the potential difference across a battery. This is always less than the EMF of the battery. This is because of the internal resistance of the battery. This idea gives us the following formula:

PD across battery = EMF of battery - voltage to be accounted for
Let us replace these values with letters to give the simpler formula:
Vexternal = E - Vinternal
Since V = IR:
Vexternal = E - IRinternal
You may also need to use the following formula to work out the external potential difference, if you are not given it:
Vexternal = IΣRexternal
You should also remember the effects of using resistors in both series and parallel circuits.
Questions
1. A 9V battery is short-circuited. The potential difference across the battery is found to be 8V, and the current is 5A. What is the internal resistance of the battery?
2. What is the EMF of the battery in the following circuit?
3. What is the internal resistance of the battery in the following circuit?
Potential Dividers

A potential divider, or potentiometer, consists of a number of resistors, and a voltmeter. The voltage read by the voltmeter is determined by the ratio of the resistances on either side of the point at which one end of the voltmeter is connected.
To understand how a potential divider works, let us consider resistors in series. The resistances add up, so, in a circuit with two resistors:
If we apply Ohm's law, remembering that the current is constant throughout a series circuit:
Multiply by current (I):
So, just as the resistances in series add up to the total resistance, the potential differences add up to the total potential difference. The ratios between the resistances are equal to the ratios between the potential differences. In other words, we can calculate the potential difference across a resistor using the formula:
In many cases, you will be told to assume that the internal resistance of the power source is negligible, meaning that you can take the total potential difference as the EMF of the power source.
A potential divider may work by combining a variable resistor such as an LDR or thermistor with a constant resistor, as in the diagram below. As the resistance of the variable resistor changes, the ratio between the resistances changes, so the potential difference across any given resistor changes.
Alternatively, a potential divider may be made of many resistors. A 'wiper' may move across them, varying the number of resistors on either side of the wiper as it moves, as in the following diagram:
Questions
1. A 12 kΩ resistor and a 20 kΩ resistor are connected to a 9V battery. A voltmeter is connected across the 12kΩ resistor. What is the reading on the voltmeter? (Assume negligible internal resistance.)
2. A potential divider consists of 100 5Ω resistors, with a wiper which moves on one resistor for every 3.6° a handle connected to it turns. The wiper is connected to a voltmeter, and the circuit is powered by a 120V power source with negligible internal resistance. What is the reading on the voltmeter when the handle turns 120°?
3. A 9V battery with internal resistance 0.8Ω is connected to 3 resistors with conductances of 3, 2 and 1 Siemens. A voltmeter is connected across the 3 and 2 Siemens resistors. An ammeter is placed in the circuit, between the battery and the first terminal of the voltmeter, and reads 2A. What is the reading on the voltmeter?
Sensors
A sensor is a device which converts a physical property into an electrical property (such as resistance). A sensing system is a system (usually a circuit) which allows this electrical property, and so the physical property, to be measured.
Temperature Sensor

A common example of a sensing system is a temperature sensor in a thermostat, which uses a thermistor. In the most common type of thermistor (an NTC), the resistance decreases as the temperature increases. This effect is achieved by making the thermistor out of a semiconductor. The thermistor is then used in a potential divider, as in the diagram on the right. In this diagram, the potential difference is divided between the resistor and the thermistor. As the temperature rises, the resistance of the thermistor decreases, so the potential difference across it decreases. This means that potential difference across the resistor increases as temperature increases. This is why the voltmeter is across the resistor, not the thermistor.
Properties
There are three main properties of sensing systems you need to know about:
Sensitivity
This is the amount of change in voltage output per unit change in input (the physical property). For example, in the above sensing system, if the voltage on the voltmeter increased by 10V as the temperature increased by 6.3 °C:
V/°C
Resolution
This is the smallest change in the physical property detectable by the sensing system. Sometimes, the limiting factor is the number of decimal places the voltmeter can display. So if, for example, the voltmeter can display the voltage to 2 decimal places, the smallest visible change in voltage is 0.01V. We can then use the sensitivity of the sensor to calculate the resolution.
<math>R = \frac{0.01}{
Response Time
This is the time the sensing system takes to display a change in the physical property it is measuring. It is often difficult to measure.
Signal Amplification
Sometimes, a sensing system gives a difference in output voltage, but the sensitivity is far too low to be of any use. There are two solutions to this problem, which can be used together:
Amplification
An Amplifier is an electronic device or circuit which is used to increase the magnitude of the signal applied to its input. An Amplifier is a generic term used to describe a circuit which produces and increased version of its input signal. An amplifier can be placed in the system, increasing the signal. The main problem with this is that the signal cannot exceed the maximum voltage of the system, so values will be chopped off of the top and bottom of the signal because it is so high.
Wheatstone Bridge

This solution is far better, especially when used prior to amplification. Instead of using just one pair of resistors, a second pair is used, and the potential difference between the two pairs (which are connected in parallel) is measured. This means that, if, at the sensing resistor (e.g. thermistor / LDR) the resistance is at its maximum, a signal of 0V is produced. This means that the extremes of the signal are not chopped off, making for a much better sensor.
Questions
An LDR's resistance decreases from a maximum resistance of 2kΩ to a minimum resistance of 0Ω as light intensity increases. It is used in a distance sensing system which consists of a 9V power supply, a 1.6 kΩ resistor, the LDR and a multimeter which displays voltage to 2 decimal places measuring the potential difference across one of the two resistors.
1. Across which resistor should the multimeter be connected in order to ensure that, as the distance from the light source to the sensor increases, the potential difference recorded increases?
2. In complete darkness, what voltage is recorded on the multimeter?
3. When a light source moves 0.5m away from the sensor, the voltage on the multimeter increases by 2V. What is the sensitivity of the sensing system when using this light source, in V m−1?
4. When the same light source is placed 0m from the sensor, the potential difference is 0V. When the light source is 1m away, what voltage is displayed on the multimeter?
5. What is the resolution of the sensing system?
6. Draw a circuit diagram showing a similar sensing system to this, using a Wheatstone bridge and amplifier to improve the sensitivity of the system.
7. What is the maximum potential difference that can reach the amplifier using this new system (ignore the amplification)?
8. If this signal were to be amplified 3 times, would it exceed the maximum voltage of the system? What would the limits on the signal be?
Resistivity and Conductivity
Resistivity and conductivity are material properties: they apply to all examples of a certain material anywhere. They are not the same as resistance and conductance, which are properties of individual artefacts. This means that resistivity and conductivity only apply to a given object. They describe how well a material resists or conducts an electric current.
Symbols and Units
Resistivity is usually represented by the Greek letter rho (ρ), and is measured in Ω m. Conductivity is usually represented by the Greek letter sigma (σ), and is measured in S m−1.
Formulae
The formula relating resistivity (ρ) to resistance (R), cross-sectional area (A) and length (L) is:
Conductivity is the reciprocal of resistivity, just as conductance (G) is the reciprocal of resistance. Hence:
You should be able to rearrange these two formulae to be able to work out resistance, conductance, cross-sectional area and length. For example, it all makes a lot more sense if we write the first formula in terms of ρ, A and L:
From this, we can see that the resistance of a lump of material is higher if it has a higher resistivity, or if it is longer. Also, if it has a larger cross-sectional area, its resistance is smaller.
Questions
1. A material has a conductivity of 106 S m−1. What is its resistivity?
2. A pure copper wire has a radius of 0.5mm, a resistance of 1 MΩ, and is 4680 km long. What is the resistivity of copper?
3. Gold has a conductivity of 45 MS m−1. What is the resistance of a 0.01m across gold connector, 0.05m long?
4. A strand of metal is stretched to twice its original length. What is its new resistance? State your assumptions.
5. Which has the greater resistivity: a plank or a piece of sawdust, made from the same wood? 6. What is the relation between time and resistance and length? Worked Solutions
Semiconductors

A semiconductor has a conductivity between that of a conductor and an insulator. They are less conductive than metals, but differ from metals in that, as a semiconductor heats up, its conductivity rises. In metals, the opposite effect occurs.
The reason for this is that, in a semiconductor, very few atoms are ionised, and so very few electrons can move, creating an electric current. However, as the semiconductor heats up, the covalent bonds (atoms sharing electrons, causing the electrons to be relatively immobile) break down, freeing the electrons. As a result, a semiconductor's conductivity rises at an increasing rate as temperature rises.
Examples of semiconductors include silicon and germanium. A full list of semiconductor materials is available at Wikipedia. At room temperature, silicon has a conductivity of about 435 μS m−1.
Semiconductors are usually 'doped'. This means that ions are added in small quantities, giving the semiconductor a greater or lesser number of free electrons as required. This is controlled by the charge on the ions.
Questions
1. What is the resistivity of silicon, at room temperature?
2. What sort of variable resistor would a semiconductor be useful in?
3. If positive ions are added to silicon (doping it), how does its conductivity change? Worked Solutions
4. What is a practical application of a Semi-Conductor?
See also
- The book on Semiconductors.
Stress, Strain & the Young Modulus
Stress
Stress is a measure of the internal force an object is experiencing per unit cross sectional area:
Where σ is stress (in Newtons per square metre or, equivalently, Pascals), F is force (in Newtons, commonly abbreviated N), and A is the cross sectional area of the sample.
This is identical to the formula for pressure. Two distinctions should be made between stress and pressure: Firstly, while pressure is typically used to describe fluids (liquids or gases), stress is used to describe solids. Secondly, while pressure can only act perpendicular to a surface, stress is also able to act parallel to a surface. Stresses acting parallel to a surface are known as shear stresses.
Tensile Strength
The (ultimate) tensile strength is the maximum tensile stress of a material can experience before breaking (and a change of cross-sectional area as a result) will occur.
Yield Stress
On a stress strain graph beyond the yield point (or elastic limit) the material will no longer return to its original length. This means it has become permanently deformed. Therefore the yield stress is the level of stress at which a material will deform permanently. This is also known as yield strength.
Strain
Stresses lead to strain (or deformation). Putting pressure on an object causes it to stretch. Strain is a measure of how much an object is being stretched. The formula for strain is:
,
where is the original length of a bar being stretched, and l is its length after it has been stretched. Δl is the extension of the bar, the difference between these two lengths.
Young's Modulus
Young's Modulus is a measure of the stiffness of a material, and describes how much strain a material will undergo (i.e. how much it will stretch) as a result of a given amount of stress. The Young's Modulus E of a material is calculated as:
The values for stress and strain must be taken at as low a stress level as possible, provided a difference in the length of the sample can be measured. Strain has no units due to simply being the ratio between the extension and original length of a material, so Young's Modulus is measured by the same units as stress, i.e. newtons per square metre (Nm-2) or Pascals (Pa). As Young's Modulus is measured per unit area, it is an intensive property, meaning it only depends on the material being used, and not on the size of the material.
Stress-Strain Graphs

Stress (σ) can be graphed against strain (ε). The toughness of a material (i.e., how much it resists stress, in J m−3) is equal to the area under the curve, between the y-axis and the fracture point. Graphs such as the one on the right show how stress affects a material. This image shows the stress-strain graph for low-carbon steel. It has three main features:
Elastic Region
In this region (between the origin and point 2), the ratio of stress to strain (Young's modulus) is constant, meaning that the material is obeying Hooke's law, which states that a material is elastic (it will return to its original shape) if force is directly proportional to extension of the material
Hooke's Law
Hooke's law of elasticity is an approximation that states that the Force F (load) is in direct proportion with the extension (denoted by x or e) of a material, provided this load does not exceed the proportional limit. The constant k is inherent to the material being measured. Materials for which Hooke's law is a useful approximation are known as linear-elastic, or 'elastic materials'.
The relation is often denoted
The work done to stretch a wire or the Elastic Potential Energy is equal to the area of the triangle on a Tension/Extension graph, but can also be expressed as
Plastic Region
In this region (between points 2 and 3), the rate at which extension is increasing is going up, and the material has passed the elastic limit - it will no longer return to its original shape when the load is removed, and will now undergo plastic (permanent) deformation. After point 1, the amount of stress decreases due to necking at one point in the specimen. If the stress were recorded where the necking occurs we would observe an upward curve and an increase in stress due to this reduction in area(stress = Force / area, thus stress increases during necking). The material will now 'give' and extend more under less force.
Fracture Point
At point 3, the material has been fractured and so no further measurements can be taken.
Other Typical Graphs
In a brittle material, such as glass or ceramics, the stress-strain graph will have an extremely short elastic region, and then will fracture. There is no plastic region on the stress-strain graph of a brittle material.
Questions
- 100N of force are exerted on a wire with cross-sectional area 0.50mm2. How much stress is being exerted on the wire?
- Another wire has a tensile strength of 70MPa, and breaks under 100N of force. What is the cross-sectional area of the wire just before breaking?
- What is the strain on a Twix bar (original length 10 cm) if it is now 12 cm long?
- What is this strain, expressed as a percentage?
- 50N are applied to a wire with a radius of 1mm. The wire was 0.7m long, but is now 0.75m long. What is the Young's Modulus for the material the wire is made of?
- Glass, a brittle material, fractures at a strain of 0.004 and a stress of 240 MPa. Sketch the stress-strain graph for glass.
- (Extra nasty question which you won't ever get in an exam) What is the toughness of glass?
- Wire has a tensile strength of 0.95Mpa, and breaks under 25N of force. what is the cross-sectional area of the wire before and after breaking?
- Estimating the Young's Modulus of a diamond to be 900GPa,[1] how many centimeters would a diamond cylinder stretch if it had a 2 millimeter diameter and a length of 10 kilometers? Assume the force to be 10 Newtons. Also assume that the diamond does not break (it is currently unknown whether this would break the diamond and calculations on an object this bizarre should probably not be trusted anyway.)
- How many pounds is 10 Newtons? (This question is so nasty you should either skip it or just google the question! The "Worked Solutions" below is a botched attempt not worth repeating.)
Metals

There are several physical properties of metals you need to know about:
Electrical Properties
Metals on a microscopic scale consist of positive metal ions in 'sea' of free (delocalised) electrons. The electrons act are able to freely move around the metallic lattice, in and between the ions. Metallic bonding is therefore described as non-directional, in contrast to the directional bonds found between atoms in covalently-bonded materials (e.g. carbon atoms in diamond).
As the delocalised electrons each carry charge and are able to move freely, they are described as 'mobile charge carriers'. Electricity is simply the flow of charged particles, and so the presence of a high number of mobile charge carriers per unit volume in metals means they tend to be very effective conductors. In contrast, ionically-bonded materials involve ions in fixed positions. The ions are charged particles, however as they are immobile they are not described as mobile charge carriers, making ionic substances (eg sodium chloride) unable to carry electric current when solid.
When a current flows through a metal, the delocalised electrons collide with the metal ions, transferring kinetic energy to them, resulting in an increase in the temperature of the metal. As the temperature of the metal increases and its metal ions vibrate more, electrons are more likely to collide with them, meaning the flow of current is resisted. The resistance of a metal therefore increases with temperature.
Similarly, as higher currents involve a faster flow of electrons, they cause more collisions between electrons and metal ions, and so cause the conducting material to increase in temperature. This is exemplified by the UK power grid - electricity is transferred throughout the country at extremely high voltages (typically 275kV or 400kV) but low currents, therefore allowing the electricity to travel at a high power without significant heating occurring in the wires.
Mechanical Properties
This 'sea' of free electrons can also be described as a glue that does not dry. The negatively charged electrons have an electro-static attraction to the positively charged metal ions. This is what holds the entire metal structure together and gives metals their strength, i.e. the ability of the material to resist coming apart.
It also means that metals will change shape without coming apart completely (breaking). This is known as plastic deformation, which is when a material changes permanently (unlike elastic deformation) and also does not fracture (like when a glass fibre is stretched too far). Pure metals are usually incredibly ductile and malleable and can worked into a wide variety of shapes. The sea allows the atoms to move past each other. Atoms can move out of their place on the lattice. Other atoms can then go and fill that place. Entire layers of atoms in a crystal lattice can slip past one another, and the free electrons flowing between will keep them stuck together [see dislocations]. The glue allows movement of atoms without breaking the metallic bond, i.e. the electrostatic attraction between the free-flowing electrons and the positive ions.
Of course, metals do eventually fracture, however, they tend to show necking first.
This could not happen in a material where the strength comes from covalent bonds because the electrons need to be in specific positions. When ionic bonds or covalent bonds are broken, they do not generally go back together. Materials held together entirely by covalent or ionic bonds tend to be very brittle. The bonding in metals is not directional and not permanent. This gives metals their strength and plasticity, their most useful mechanical properties.
List of Mechanical Properties
Stiffness
As the electrostatic attraction between the sea of electrons and metal ions hold the layers quite strongly, metals resist deformation quite well. This is especially true with alloys, where atoms of different sizes prevent the layers slipping past each other.
Ductile
Since the bonding is non-directional and non-permanent, with electrons that are free to move around, atoms can move about and slide past each other. This makes metals relatively ductile.
Toughness
Metals are tough for the same reason as they are ductile: the positive ions can slide past each other while still remaining together. So, instead of breaking apart, they change shape, resulting in increased toughness. This effect is called plasticity. When a tough material breaks the ratio of 'energy used / new surface area created' is very large.
Elasticity
When a metal is stretched, it can return to its original shape because the sea of electrons which bonds the ions together can be stretched as well.
Brittle
The opposite of tough: a material is likely to crack or shatter upon impact or force. It will snap cleanly due to defects and cracks. Metals can be brittle in certain circumstances, and a metal can be made more brittle by alloying or by work hardening.
Malleability
Metals are malleable because their atoms are arranged in flat planes that can slide past each other. Their bonds are non-directional. Metals also contain dislocations which mean that ions in the structure can be moved unilaterally rather than as a whole layer, which takes less energy to do.
Thermal Properties
Metals conduct electricity well for 2 main reasons. Firstly, they are in a lattice. The atoms are arranged both closely and neatly. This means that atoms transmit forces very efficiently through the material, so thermal vibrations pass heat energy along easily. This effect is also observed in ionic lattices and in silicon and diamond which are covalent lattices.
Secondly, the free electrons move more when heated, which is another method of passing heat through the lattice.
Transformation
Diffusive transformation: occur when the planes of atoms in the material move past each other due to the stresses on the object. This transformation is permanent and cannot be recovered from due to energy being absorbed by the structure
Diffusionless transformation: occurs where the bonds between the atoms stretch, allowing the material to deform elastically. An example would be rubber or a shape memory metal/alloy (often referred to as SMA) such as a nickel-titanium alloy. In the shape memory alloy the transformation occurs via the change of phase of the internal structure from martensitic to deformed martensitic, which allows the SMA to have a high percentage strain (up to 8% for some SMA's in comparison to approximately 0.5% for steel). If the material is then heated above a certain temperature the deformed martensite will form austenite, which returns to twinned martensite after cooling.
Arrangement of atoms
Metal atoms form lattices. These are neat ordered rows of atoms that stack together to make layers, which in turn stack neatly to make a 3D structure. The fact metals stay in ordered structures is key to their properties. The neat ordered rows will stretch billions and billions of atoms across. However, they do not go on forever. Metals are usually formed from a molten state. When the liquid solidifies, this happens in many places at once. Therefore many crystals form at once, and the crystals are oriented randomly with respect to one another. Metals are polycrystalline.
How grains affect the mechanical properties is beyond the scope of the A-level course, however, as a rule of thumb, smaller grains mean a higher strength. Single crystal metals can be grown, and they have interesting unique properties related to their geometry. However, this is a difficult and specialised process, but single crystal metals can be used for turbine blades inside aeroplane engines.
Questions
1. Would you expect a metal to have more or less conductivity than a semiconductor? Why?
2. How can the stress-strain graph for a metal be explained in terms of ions in a sea of electrons?
3. As a metal heats up, what happens to its conductivity? Why?
Polymers
A simple polymer consists of a long chain of monomers (components of molecules) joined by covalent bonds. A polymer usually consists of many of these bonds, tangled up. This is known as a bulk polymer.
Types
A bulk polymer may contain two types of regions. In crystalline regions, the chains run parallel to each other, whereas in amorphous regions, they do not. Intermolecular bonds are stronger in crystalline regions. A polycrystalline polymer consists of multiple regions, in which the chains point in a different direction in each region.


Properties
Transparency
Polymers which are crystalline are usually opaque or translucent. As a polymer becomes less polycrystalline, it becomes more transparent, whilst an amorphous polymer is usually transparent.[1]
Elasticity
In some polymers, such as polyethene, the chains are folded up. When they are stretched, the chains unravel, stretching without breaking. When the stress ceases, they will return to their original shape. If, however, the bonds between the molecules are broken, the material reaches its elastic limit and will not return to its original shape.
Stiffness
Polymer chains may be linked together, causing the polymer to become stiffer. An example is rubber, which, when heated with sulfur, undergoes a process known as vulcanization. The chains in the rubber become joined by sulfur atoms, making the rubber suitable for use in car tyres. A stiffer polymer, however, will usually be more brittle.
Plasticity
When a polymer is stretched, the chains become parallel, and amorphous areas may become crystalline. This causes an apparent change in colour, and a process known as 'necking'. This is when the chains recede out of an area of the substance, making it thinner, with fatter areas on either side.
Conductivity
Polymers consist of covalent bonds, so the electrons are not free to move according to potential difference. This means that polymers are poor conductors.
Boiling Point
Polymers do not have boiling points. This is because, before they reach a theoretical boiling point, polymers decompose. Some polymers do not have melting points for the same reason.
Questions
1. Different crystalline structures have different refractive indexes. Why does this mean that a polycrystalline polymer is translucent?
2. What sort of polymer is a pane of perspex?
3. What sort of polymer does the pane of perspex become when shattered (but still in one piece)?
4. What sort of polymer is a rubber on the end of a pencil?
5. What happens to the translucency of an amorphous polymer when it is put under stress?
References
- ↑ C. A. Heaton, The Chemical industry, page 113.
=
Understanding Processes
=
What is a wave?
At this point in the course, it is easy to get bogged down in the complex theories and equations surrounding 'waves'. However, a better understanding of waves can be gained by going back to basics, and explaining what a wave is in the first place.
Definitions
A wave, at its most basic level, is a repeated disturbance that spreads out and transfers energy as it moves forwards. Water ripples, light and sound all do this.
The image below shows a waveform. It plots distance through the medium on the x-axis (e.g. distance along the surface of water), and the amount of disturbance on the y-axis (e.g. distance from where the surface would be if the water was not disturbed by ripples). The amount of disturbance is known as the displacement. Waves tend to keep the same maximum displacement. This is known as the amplitude.
The distance between two equivalent points in a wave, along the direction in which the wave travels, is known as the wavelength. The 'peaks' or 'troughs' (where displacement is at a maximum or minimum) are usually chosen as these are the best points of a wave to measure. This is the distance a wave needs to travel in order to repeat itself, or the distance of one oscillation.
The nature of a wave
This raises the question "How can the disturbance itself move?" In some cases, this is easy to answer. Lots of waves travel through a material, in which case it is the material of the medium that is being disturbed. Such waves are called "mechanical waves", which require a material medium to travel in in order to exist. The easiest example to think about is a water wave. One area moves up, pulling the next one up with it. The water in this area gains potential energy. Eventually, pressure and gravity pull the water back down, and they gain kinetic energy which is again passed onto the next area. This allows the process to repeat, spread out and keep passing energy on.
The nature of electromagnetic waves, which includes light, is much more difficult to explain. There is a section below that discusses this.

Velocity, frequency and wavelength
You should remember the equation v = fλ from earlier in this course, or from GCSE. v is the velocity at which the wave travels through the medium, in ms−1, f (or nu, ν) is the frequency of the wave, in Hz (how many waves pass through a point each second), and λ is the wavelength, in m.
This is analogous to walking. Frequency would be the number of steps taken in a unit of time, equivalent to how many times the wave oscillates in a unit of time. The wavelength is equivalent to how long each step is. As most waves have a set speed (e.g. the speed of light or speed of sound), as wavelength goes up the frequency goes down, and vice versa. They are inversely proportional. When walking, if you take steps more often, each step must make you travel less distance if you are to continue walking at the same speed.
This equation applies to electromagnetic waves, but you should remember that there are different wavelengths of electromagnetic radiation, and that different colours of visible light have different wavelengths. You also need to know the wavelengths of the different types of electromagnetic radiation:
The problem of explaining the nature of light
Until relatively recently, scientists struggled to explain what light was. In the past they could only look at what light could do and make educated guesses. Developing ideas from evidence is extremely important in science. Using ideas and to make to explain evidence is extremely important in science. Models are ideas that represent reality. Often, models are developed to explain existing evidence. A good model will predict unobserved behaviour.
Could light be made of particles?
Some scientists have historically suggested that light is a stream of particles. This would explain away the need for a medium to travel through. It would explain why light travels more slowly in denser materials, unlike sound. It also explains why light can travel in straight lines, as well the angle of incidence is equal to the angle of reflection when light "bounces" off a surface. However, there are some behaviours that a particle model does not explain well.
Light as a wave?
Light was observed to have some properties of waves, e.g. being able to spread out. This behaviour seemed to be best explained by waves. As such, a lot of scientists historically liked to think of light as a wave. However, waves were thought of as disturbances. The proponents of a wave model struggled to explain how light could move through a vacuum. This is a place with no material to disturb. Sound cannot pass through a vacuum at all because there is no material to disturb and pass energy onto. The fact light could move through a vacuum was very problematic to using waves as an explanation.
In order to get around this, some scientists came up with the idea of 'ether'. They said there must be a mysterious and undetectable substance that exists everywhere for light to disturb in order to move in. However, the ether theory had problems, including being unable to detect any. It is not a theory accepted by modern physicists.
The evidence
New experiments kept showing light to have more and more behaviour unique to waves. The most important was perhaps interference. This made physicists accept that it must be a wave. Despite not being able to explain what light was a wave in, accepting this was the only way to explain its behaviour.
Types of Waves
Waves can be categorised based on how the disturbance moves relative to the wave. A wave which causes disturbance parallel to the direction of its travel is known as a longitudinal wave, whereas a wave which causes disturbance perpendicular to the direction of its travel is known as a transverse wave.
| Longitudinal wave (e.g. sound) | Transverse wave (e.g. light) |
|---|---|

|

|
Superposition / Interference
Note that disturbance is often described as a displacement, which is a vector quantity. Vectors at any point simply add up.
One feature of waves is that they superpose. When they are travelling in the same place in the medium at the same time, they both affect the medium independently. The vector quantities of displacement simply add up and the material is displaced by the vector sum. If two waves do this whilst moving in opposite directions, after passing through one another, they will carry on unaffected.
This is often referred to as as "interference". Some physicists do not like this word as it implies any wave interfering is unwanted, or "noise". However, this effect can be extremely useful e.g. when heating food in a microwave oven.
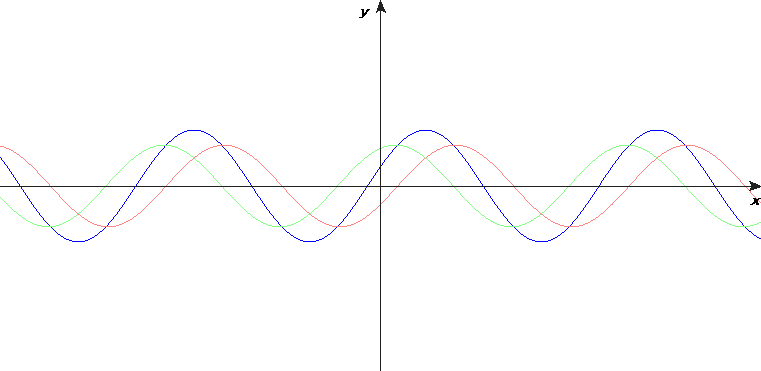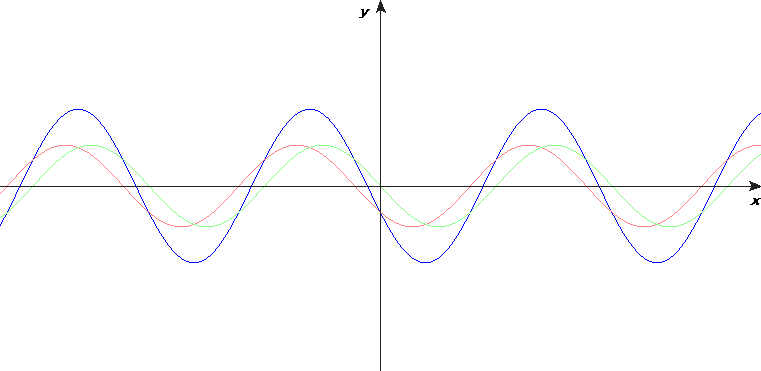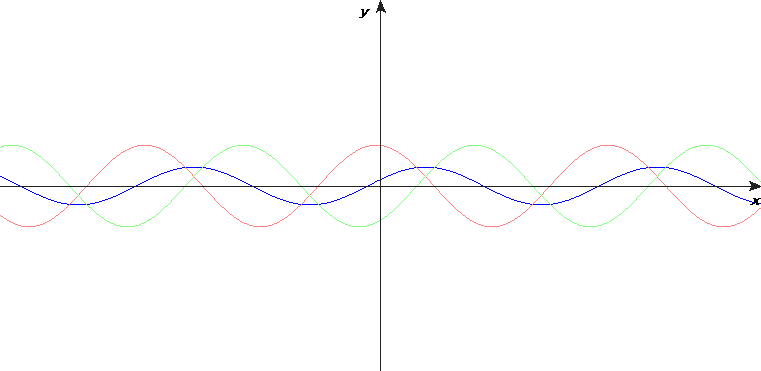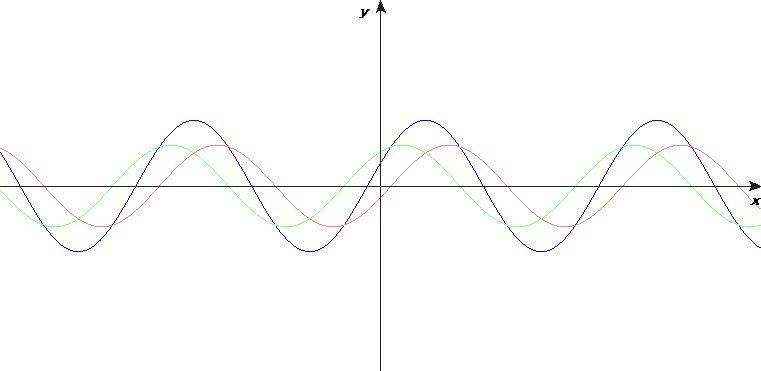
Consider two identical waveforms being superposed on each other. The resultant waveform will be like the two other waveforms, except its amplitude at every point will be twice as much. This is known as constructive interference. Alternatively, if one waveform moves on by half a wavelength, but the other does not, the resultant waveform will have no amplitude, as the two waveforms will cancel each other out. This is known as destructive interference. Both these effects are shown in the diagram below:
These effects occur because the wavefronts are travelling through a medium, but electromagnetic radiation also behaves like this, even though it does not travel through a medium.
Questions

1. What is a wave?
2. Through what medium are sound waves propagated?
3. What aspects of the behaviour of light make it look like a wave?
4. What aspects of the behaviour of light make it look like a particle?
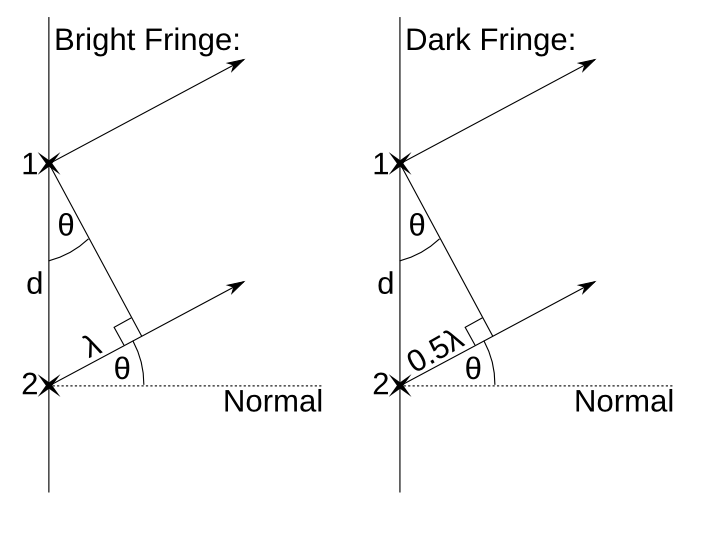
5. Consider the diagram on the right. White light is partially reflected by the transparent material. Some of the light, however, is refracted into the transparent material and reflected back by the opaque material. The result is two waves travelling in the same place at the same time at the same polarisation(the light is not a single beam). Why does, say, the red light disappear? (Variations on this question are popular with examiners.)
6. What is the wavelength of green light?
7. The lowest frequency sound wave humans can hear has a frequency of approximately 20 Hz. Given that the speed of sound in air is 343ms−1, what is the wavelength of the lowest frequency human-audible sound?
Phasors
Consider the image on the right. It shows a wave travelling through a medium. The moving blue dot represents the displacement caused to the medium by the wave. It can be seen that, if we consider any one point in the medium, it goes through a repeating pattern, moving up and down, moving faster the nearer it is to the centre of the waveform. Its height is determined by the amplitude of the wave at that point in time. This is determined by a sine wave.

Phasors are a method of describing waves which show two things: the displacement caused to the medium, and the point in the repeating waveform which is being represented. They consist of a circle. An arrow moves round the circle anticlockwise as the wave pattern passes. For every wavelength that goes past, the arrow moves 360°, or 2πc, starting from the right, as in trigonometry. The angle of the arrow from the right is known as the phase angle, and is usually denoted θ, and the radius of the circle is usually denoted a. The height of the point at the end of the arrow represents the displacement caused by the wave to the medium, and so the amplitude of the wave at that point in time. The time taken to rotate 360° is known as the periodic time, and is usually denoted T.
Phase difference is the difference between the angles (θ) of two phasors, which represent two waves. It is never more than 180°, as, since the phasor is moving in a circle, the angle between two lines touching the circumference will always be less than or equal to 180°. It can also be expressed in terms of λ, where λ is the total wavelength (effectively, 360°). You can use trigonometry to calculate the displacement from the angle, and vice-versa, provided you know the radius of the circle. The radius is equal to the maximum amplitude of the wave.
Phasors can be added up, just like vectors: tip-to-tail. So, for example, when two waves are superposed on each other, the phasors at each point in the reference material can be added up to give a new displacement. This explains both constructive and destructive interference as well. In destructive interference, the phasors for each wave are pointing in exactly opposite directions, and so add up to nothing at all. In constructive interference, the phasors are pointing in the same direction, so the total displacement is twice as much.
Questions
1. A sine wave with wavelength 0.1m travels through a given point on the surface of the sea. A phasor arrow representing the effect of this wave on this point rotates 1000°. How many wavelengths have gone past in the time taken for the phasor to rotate this much?
2. A sine wave has a maximum amplitude of 500 nm. What is its amplitude when the phasor has rotated 60° from its start position?
3. Two waves have a phase difference of 45°. When the first wave is at its minimum amplitude of -0.3m, what is the total amplitude of the superposed waveforms?
Standing Waves
When two coherent waves - waves of equal frequency and amplitude - travel in opposite directions through the same area, an interesting superposition effect occurs, as is shown in the following animation:

Some areas of the resultant waveform consistently have an amplitude of 0. These are known as nodes. At other points (half-way between the nodes), the resultant waveform varies from twice the amplitude of its constituent waveforms in both directions. These points are known as antinodes. Everywhere in between the nodes and antinodes varies to a lesser degree, depending on its position.
This effect only occurs if the two waveforms have the same amplitude and frequency. If the two waves have different amplitudes, the resultant waveform is similar to a standing wave, except that it has no nodes, and 'moves'.
Because of these conditions, standing waves usually only occur when a waveform is reflected back on itself. For example, in a microwave oven, the microwaves are reflected by the metal on the other side of the oven from the transmitter. This creates nodes and antinodes. Since nothing cooks at the nodes, a turntable is necessary to ensure that all of the food passes through the antinodes and gets cooked.
Frequencies

Consider a string, attached at either end, but allowed to move freely in between. If you pluck it, you create a wave which travels along the string in both directions, and is reflected at either end of the string. This process keeps on happening, and so a standing wave pattern is created. The string goes up, and then down, as shown in the first row of the diagram on the right. If you imagine the top arc as the first half of a waveform, you can see that when the string is vibrating at the fundamental frequency, the string is half as long as the wavelength: it is ½λ long. Therefore, λ=2L
If you were to pinch the string in the middle, and then pluck it on one side, a different standing wave pattern would be generated. By plucking, you have created an antinode, and by pinching, you have created a node. If you then let go of the string, the standing wave pattern spreads, and the string length now equals the wavelength. This is known as the first harmonic.
As you pinch the string in descending fractions (½, ⅓, ¼, etc.), you generate successive harmonics, and the total length of the string is equal to additional ½λ wavelengths.
Pipes

Consider a pipe which is open at one end, and closed at the other. In pipes, waves are reflected at the end of the pipe, regardless of whether it is open or not. If you blow across the end of the tube, you create a longitudinal wave, with the air as the medium. This wave travels down the tube, is reflected, travels back, is reflected again, and so on, creating a standing wave pattern.
The closed end of the pipe must be a node; it is the equivalent of pinching a string. Similarly, the open end must be an antinode; blowing across it is the equivalent of plucking the string.
Harmonics can be present in pipes, as well. This is how musical instruments work: an open hole in a wind instrument creates an antinode, changing the frequency of the sound, and so the pitch.
Questions
1. The air in a 3m organ pipe is resonating at the fundamental frequency. Organ pipes are effectively open at both ends. What is the wavelength of the sound?
2. A string is vibrating at the second harmonic frequency. How many wavelengths long is the standing wave created?
3. Express, in terms of λ, the length of a pipe which is closed at one end, where λ is the length of one wave at the fundamental frequency.
Young's Slits

You should be familiar with the idea that, when light passes through a slit, it is diffracted (caused to spread out in arcs from the slit). The amount of diffraction increases the closer the slit width is to the wavelength of the light. Consider the animation on the right. Light from a light source is caused to pass through two slits. It is diffracted at both these slits, and so it spreads out in two sets of arcs.
Now, apply superposition of waves to this situation. At certain points, the peaks (or troughs) of the waves will coincide, creating constructive interference. If this occurs on a screen, then a bright 'fringe' will be visible. On the other hand, if destructive interference occurs (a peak coincides with a trough), then no light will be visible at that point on the screen.
Calculating the angles at which fringes occur
If we wish to calculate the position of a bright fringe, we know that, at this point, the waves must be in phase. Alternatively, at a dark fringe, the waves must be in antiphase. If we let the wavelength equal λ, the angle of the beams from the normal equal θ, and the distance between the slits equal d, we can form two triangles, one for bright fringes, and another for dark fringes (the crosses labelled 1 and 2 are the slits):
The length of the side labelled λ is known as the path difference. For bright fringes, from the geometry above, we know that:
Therefore:
However, bright fringes do not only occur when the side labelled λ is equal to 1 wavelength: it can equal multiple wavelengths, so long as it is a whole wavelength. Therefore
,
where n is any integer.
Now consider the right-hand triangle, which applies to dark fringes. We know that, in this case:
We can generalise this, too, for any dark fringe. However, if 0.5λ is multiplied by an even integer, then we will get a whole wavelength, which would result in a bright, not a dark, fringe. So, n must be an odd integer in the following formula:
Calculating the distances angles correspond to on the screen
At this point, we have to engage in some slightly dodgy maths. In the following diagram, p is path difference, L is the distance from the slits to the screen and x is the perpendicular distance from a fringe to the normal:
Here, it is necessary to approximate the distance from the slits to the fringe as the perpendicular distance from the slits to the screen. This is acceptable, provided that θ is small, which it will be, since bright fringes get dimmer as they get further away from the point on the screen opposite the slits. Hence:
If we substitute this into the equation for the path difference p:
So, at bright fringes:
, where n is an integer.
And at dark fringes:
, where n is an odd integer.
You may have noticed that is not precisely the distance from a fringe to the normal, differing from it by the amount . However, in a diffraction grating, the distance between the slits is negligible in comparison to , so it may be ignored.
Diffraction Grating
A diffraction grating consists of a lot of slits with equal values of d. As with 2 slits, when , peaks or troughs from all the slits coincide and you get a bright fringe. Things get a bit more complicated, as all the slits have different positions at which they add up, but you only need to know that diffraction gratings form light and dark fringes, and that the equations are the same as for 2 slits for these fringes.
Questions
1. A 2-slit experiment is set up in which the slits are 0.03 m apart. A bright fringe is observed at an angle 10° from the normal. What sort of electromagnetic radiation was being used?
2. Light, with a wavelength of 500 nm, is shone through 2 slits, which are 0.05 m apart. What are the angles to the normal of the first three dark fringes?
3. Some X-rays, with wavelength 1 nm, are shone through a diffraction grating in which the slits are 50 μm apart. A screen is placed 1.5m from the grating. How far are the first three light fringes from the point at which the normal intercepts the screen?
Diffraction

We have already seen why fringes are visible when light passes through multiple slits. However, this does not explain why, when light is only passing through 1 slit, a pattern such as the one on the right is visible on the screen.
The answer to this lies in phasors. We already know that the phasor arrows add up to give a resultant phasor. By considering the phasor arrows from many paths which light takes through a slit, we can explain why light and dark fringes occur.
At the normal line, where the brightest fringe is shown, all the phasor arrows are pointing in the same direction, and so add up to create the greatest amplitude: a bright fringe.
At other fringes, we can use the same formulæ as for diffraction gratings, as we are effectively treating the single slit as a row of beams of light, coming from a row of slits.
Now consider the central beam of light. By trigonometry:
,
where θ = beam angle (radians), W = beam width and L = distance from slit to screen. Since θ is small, we can approximate sin θ as θ, so:
and since λ = d sin θ:
Questions
1. What is the width of the central bright fringe on a screen placed 5m from a single slit, where the slit is 0.01m wide and the wavelength is 500 nm?
And that's all there is to it ... maybe.
Finding the Distance of a Remote Object
In the final section (Section C) of the exam, you have to be able to write about how waves are used to find the distance of a remote object. I would recommend that you pick a method, and then answer the following questions about it:
1. What sort of wave does your system use? What is an approximate wavelength of this wave?
2. What sort of distance is it usually used to measure? What sort of length would you expect the distance to be?
3. Why is measuring this distance useful to society?
4. Draw a labelled diagram of your system.
5. Explain how the system works, and what data is collected.
6. Explain how the distance to the object is calculated using the data collected.
7. What limitations does your system have? (e.g. accuracy, consistency)
8. What percentage error would you expect these limitations to cause?
9. How might these problems be solved?
Examples
Some example answers to these questions are given in the following pages:
Light as a Quantum Phenomenon
We have already seen how light behaves like both a wave and a particle, yet can be proven not to be either. This idea is not limited to light, but we will start our brief look at quantum physics with light, since it is easiest to understand.
Quantum physics is the study of quanta. A quantum is, to quote Wiktionary, "The smallest possible, and therefore indivisible, unit of a given quantity or quantifiable phenomenon". The quantum of light is the photon. We are not describing it as a particle or a wave, as such, but as a lump of energy which behaves like a particle and a wave in some cases. We are saying that the photon is the smallest part of light which could be measured, given perfect equipment. A photon is, technically, an elementary particle. It is also the carrier of all electromagnetic radiation. However, its behaviour - quantum behaviour - is completely weird, so we call it a quantum.
Evidence for the Quantum Behaviour of Light

Dim Photos
The easiest evidence to understand is dim photographs. When you take a photo with very little light, it appears 'grainy', such as the image on the right. This means that the light is arriving at the camera in lumps. If light were a wave, we would expect the photograph to appear dimmer, but uniformly so. In reality, we get clumps of light distributed randomly across the image, although the density of the random lumps is higher on the more reflective materials (the nuts). This idea of randomness, according to rules, is essential to quantum physics.

Photoelectric Effect
The second piece of evidence is more complex, but more useful since a rule can be derived from it. It can be shown experimentally that when electromagnetic radiation (e.g. light) is shone onto the surface of a metal, it can cause electrons to be emitted. Shining the right type of light with a positively charged terminal nearby can generate a current if done in a vacuum.
Scientists found that the amount of light increased the amount of current, which was to be expected. They also found that lower frequency light, which has less energy also gave lower current. Again, this was not particularly surprising.
What was puzzling, however, was that when light went below a specific minimum frequency (dependent on the metal), no current was observed whatsoever. This confused scientists. No matter how much they increased the intensity with low frequency light, no electrons were emitted. This was surprising because even with sufficient energy the photoelectric effect stopped.
This does not fit in with a wave model of light. In a wave, the energy is evenly distributed along the wave front. Higher frequency waves deliver more energy, but higher intensity also means more waves arriving, which can compensate. The energy transferred depends on both. Despite light showing all of the properties of waves (diffraction, refraction, spreading out progressively) the fact metals need light with a minimum frequency to be able to free electrons is evidence that light is not a wave. The energy along the wave front should just add up and release the electron.
The minimum frequency threshold suggests there is something about the "waves" themselves that allows electrons to be released. If energy were evenly distributed around the wave front then they would. The energy would be evenly shared and build up until electrons could be released. Rethinking light as being particles, i.e. photons, better explains this. Photons have to have a one-to-one, quantised, particle interaction with electrons. A low energy photon never releases an electron.
This is analogous to how people pay. A wave model of light freeing electrons would be like people pooling their cash in order to buy something. If they don't have enough money, they can find more people to agree to contribute to the cost until there is enough money. Higher intensity light could provide more waves to contribute enough energy to share electrons. However, this is not what happens. The photon model is analogous to a group of people trying to pay for something by credit card. No matter how many people with insufficient credit try to pay, no card is accepted, and no one gets to buy the item.
Key points:
- To release electrons, light must be above a threshold frequency.
- Higher intensity light below the threshold frequency will never release photons despite having the same, or even more, energy.
- When light is above the minimum frequency, higher intensity light will give more electrons.
The Relationship between Energy and Frequency
The photoelectric effect allows us to derive an equation linking the frequency of electromagnetic radiation to the energy of each quantum (in this case, photons). This can be achieved experimentally, by exposing the metallic surface to light of different colours, and hence different frequencies. We already know the frequencies of the different colours of light, and we can calculate the energy each photon carries into the surface, as this is the same as the energy required to supply enough potential difference to cause the electron to move. The equation for the energy of the electron is derived as follows:
First, equate two formulae for energy:
Rearrange to get:
We also know that:
So, by substituting the previous equation into the equation for energy:
,
where P = power, E = energy, t = time, I = current, V = potential difference, Q = charge, e = charge of 1 electron = -1.602 x 10−19 C, ΔV = potential difference produced between anode and cathode at a given frequency of radiation. This means that, given this potential difference, we can calculate the energy released, and hence the energy of the quanta which caused this energy to be released.
Plotting frequency (on the x-axis) against energy (on the y-axis) gives us an approximate straight line, with a gradient of 6.626 x 10−34. This number is known as Planck's constant, is measured in Js, and is usually denoted h. Therefore:
In other words, the energy carried by each quantum is proportional to the frequency of the quantum. The constant of proportionality is Planck's constant.
Questions
1. How much energy does a photon with a frequency of 50 kHz carry?
2. A photon carries 10−30J of energy. What is its frequency?
3. How many photons of frequency 545 THz does a 20W bulb give out each second?
4. In one minute, a bulb gives out a million photons of frequency 600 THz. What is the power of the bulb?
5. The photons in a beam of electromagnetic radiation carry 2.5μJ of energy each. How long should the phasors representing this radiation take to rotate?
Quantum Behaviour
So far, we have identified the fact that light travels in quanta, called photons, and that these photons carry an amount of energy which is proportional to their frequency. We also know that photons aren't waves or particles in the traditional sense of either word. Instead, they are lumps of energy. They don't behave the way classically expected of them.
Many Paths
In fact, what photons do when they are travelling is to take every path possible. If a photon has to travel from point A to point B it will travel in a straight line and loop the loop and go via Alpha Centauri and take every other possible path. This is the photon's so-called 'quantum state'. It is spread out across all space.
However, just because a photon could end up anywhere in space does not mean that it has an equal probability of ending up in any given place. It is far more likely that a photon from a torch I am carrying will end up hitting the ground in front of me than it is that the same photon will hit me on the back of the head. But both are possible. Light can go round corners; just very rarely!
Calculating Probabilities
The probability of a photon ending up at any given point in space relative to another point in space can be calculated by considering a selection of the paths the photon takes to each point. The more paths considered, the greater the accuracy of the calculation. Use the following steps when doing this:
1. Define the light source.
2. Work out the frequency of the photon.
3. Define any objects which the light cannot pass through.
4. Define the first point you wish to consider.
5. Define a set of paths from the source to the point being considered, the more, the better.
6. Work out the time taken to traverse one of the paths.
7. Work out how many phasor rotations this corresponds to.
8. Draw an arrow representing the final phasor arrow.
9. Repeat steps 6-8 for each of the paths.
10. Add all the phasor arrows together, tip-to-tail.
11. Square the amplitude of this resultant phasor arrow to gain the intensity of the light at this point. It may help to imagine a square rotating around, instead of an arrow.
12. Repeat steps 4-11 for every point you wish to consider. The more points you consider, the more accurate your probability distribution will be.
13. Compare all the resultant intensities to gain a probability distribution which describes the probabilities of a photon arriving at one point to another. For example, if the intensity of light at one point is two times the intensity of light at another, then it is twice as likely that a photon will arrive at the first point than the second.
14. If all the points being considered were on a screen, the intensities show you the relative brightnesses of light at each of the points.
Examples
If we now take this method and apply it to several situations, we find that, in many cases, the results are similar to those obtained when treating light as a wave, with the exception that we can now reconcile this idea with the observable 'lumpiness' of light, and can acknowledge the fact that there is a certain probability that some light will not behave according to some wave laws.
Travelling from A to B

This is the simplest example to consider. If we consider a range of paths going from point A to point B, and calculate the phasor directions at the end of the paths, we get a resultant phasor arrow which gives us some amplitude at point B. Since there are no obstructions, at any point this far away from the source, we will get the same resultant amplitude.
It is important to note that different paths contribute to the resultant amplitude by different amounts. The paths closer to the straight line between the two points are more parallel to the resultant angle, whereas the paths further away vary in direction more, and so tend to cancel each other out. The conclusion: light travelling in straight lines contributes most to the resultant amplitude.
Young's Slits
Here, we just need to consider two paths: one through each slit. We can then calculate two phasor arrows, add them together to gain a resultant phasor arrow, and square its amplitude to gain the intensity of the light at the point the two paths went to. When calculated, these intensities give a pattern of light and dark fringes, just as predicted by the wave theory.

Reflection
This situation is very similar to what happens when light travels in a 'straight line'. The only difference is that we consider the paths which involve rebounding off an obstacle. The results are more or less the same, but the paths from which they were obtained are different. This means that we can assume the same conclusions about these different paths: that most of the resultant amplitude comes from the part of the mirror where the angle of incidence equals the angle of reflection. In other words, the likelihood is that a photon will behave as if mirrors work according to wave theory.

Refraction
Different paths have different lengths, and so photons take different amounts of time to traverse them (these are known as trip times). In the diagram on the right, the photons again traverse all possible paths. However, the paths with the smallest difference between trip times have phasor arrows with the smallest difference in direction, so the paths with the smallest trip times contribute most to the resultant amplitude. This shortest path is given by Snell's law. Yet again, quantum physics provides a more accurate picture of something which has already been explained to some degree.
Diffraction
Diffraction occurs when the photons are blocked from taking every other path. This occurs when light passes through a gap less than 1 wavelength wide. The result is that, where the amplitudes would have roughly cancelled each other out, they do not, and so light spreads out in directions it would not normally spread out in. This explains diffraction, instead of just being able to observe and calculate what happens.
Electron Behaviour as a Quantum Phenomenon

So far, we have considered how quantum physics applies to photons, the quanta of light. In reality, every other particle is also a quantum, but you only need to know about photons and electrons.
The image on the right shows what happens when you fire electrons through a pair of slits: it arrives in lumps, but you get fringes due to superposition as well. The electrons are behaving as both waves and particles. Actually, they are behaving as quanta. The equations describing quantum behaviour in electrons are similar to those describing it in photons.
Frequency and Kinetic Energy
We know that, for photons:
In suggesting that electrons are quanta, we assume that they must have a frequency at which the phasors representing them rotate. We also know that h is a constant; it does not change. So, when adapting the above equation to apply to electrons, all we need to adapt is E. In electrons, this energy is their kinetic energy. If the electron has some form of potential energy, this must first be subtracted from the kinetic energy, as this portion of the energy does not affect frequency. So:
De Broglie Wavelength
If electrons exhibit some wavelike properties, they must also have a 'wavelength', known as the de Broglie wavelength, after its discoverer. This is necessary in order to work out a probability distribution for the position of an electron, as this is the distance the electron travels for each phasor arrow rotation. The de Broglie wavelength λ is given by the equation:
,
where h = Planck's constant, p = momentum, m = mass of electron = 9.1 x 10−31kg and v = velocity of electron.
Potential Difference and Kinetic Energy
Potential difference is what causes electrons to move. You already know how power is related to charge, voltage and time:
Since power is the rate at which work is done:
We know that the charge on an electron equals -1.6 x 10−19, and that work done is energy, so:
Energy, in the SI system of units, is measured in Joules, but, sometimes it is measured in electronvolts, or eV. 1 eV is the kinetic energy of 1 electron accelerated by 1V of potential difference. So, 1 eV = 1.6 x 10−19 J.

Questions
1. An electron moves at 30,000 ms−1. What is its de Broglie wavelength?
2. What is its frequency?
3. What is its kinetic energy, in eV?
4. Given that it is travelling out of an electron gun, what was the potential difference between the anode and the cathode?
5. An electron is accelerated by a potential difference of 150V. What is its frequency?
Vectors
What is a vector?
Two types of physical quantity are scalars and vectors. Scalar quantities are simple: they are things like speed, distance, or time. They have a magnitude, but no direction. A vector quantity consists of two parts: both a scalar and a direction. For example, the velocity of an object is made up of both the speed of an object and the direction in which it is moving. Speed is a scalar; add a direction and it becomes velocity, a vector. Similarly, take a distance and give it a direction and it becomes a displacement, such as '2 miles south-east'. Distance is a scalar, whereas displacement is a vector.
Vectors and scalars are both useful. For example, if I run around the room several times and end up back where I started, I may have covered a distance of 50m. My displacement is 0 - the null vector. The null vector is the only vector which has no direction. If I want to calculate how much work I have done, I should use the distance. If I want to know where I am, I should use the displacement.
As we shall see, the directional component of a vector can be expressed in several different ways. '2 miles south-east' is the same as saying '2 miles on a bearing of 135°', or '1.4 miles east, -1.4 miles north'. The scalar component of a vector is known as the modulus of a vector.
Vector Notation
You need to be able to understand the following algebraic representations of vectors:
| Symbol | Meaning |
| A vector from point a to point b. | |
| a | A vector named 'a'. This is used in typed algebra. |
| a | A vector named 'a'. This is used in handwritten algebra. |
| or |a| or |a| | The modulus of a vector. |
Vector Components

Sometimes, it is useful to express a vector in terms of two other vectors. These two vectors are usually pointing up and right, and work similarly to the Cartesian co-ordinate system. So, for example, 'an acceleration of 3.4 ms−2 west' becomes 'a vertical acceleration of 0 ms−2 and an horizontal acceleration of -3.4 ms−2 east. However, this is a very simple example.
Consider the diagram on the right. The vector a consists of a vertical component j and a horizontal component i. a has a modulus |a|. |i| and |j| can be calculated using |a|, the angle between i and a θ and some basic trigonometry. We know that:
and
Hence:
|i| = |a| cos θ and |j| = |a| sin θ.
This will be given to you in the formula booklet in the exam.
Vector Addition

You also need to know how to add vectors together. This enables us to answer questions such as, "If I travel 5 miles north-west and then 6 miles east, where am I?", or "If I accelerate at 3 ms-2 in a northerly direction, and accelerate south-east at 1 ms-2, what is my total acceleration?". Vectors can be added 'tip-to-tail'; that is to say, the resultant vector is equal to 'travelling' the first vector, and then travelling the second vector.
This is shown in the diagram on the left. When vectors a and b are added together, the resultant vector a + b is produced, joining the tail of the first vector to the tip of the last, with the vectors joined together. In practise, the easiest way to add two vectors together is to calculate (if you do not already know this) the vertical and horizontal components, and add them all together to get two total vertical and horizontal components. You can then use Pythagoras' theorem to calculate the modulus of the resultant vector, and some more basic trigonometry to calculate its direction.

In algebra:
and ,
where a1 ... an are the vectors to be added together, i1 ... in are their horizontal components, j1 ... jn are their vertical components, and θ is the angle between the θ=0 line and the resultant vector Σan, as shown in the diagram on the right.
Predicting Parabolas

If you use a diagram to represent vectors (making the lengths of the arrows proportional to the modulus of the vectors they represent, and the directions equal), you can predict graphically the trajectory an object (such as a ball) will take. Use the following steps:
- Draw a vector to represent the velocity of the ball (in ms−1). Since this is the number of metres travelled in 1 second, and each step of the process is 1 second long, this vector represents both the velocity and the displacement of the ball, i.e.
- Copy this vector, and connect its tail to the tip of the first vector. This new vector represents the velocity and displacement that the ball would have had over the next second, if gravity did not exist.
- Draw another vector to represent the change in velocity due to gravity (9.81 ms−2) on Earth. This should be pointing downwards, and be to the same scale as the other vectors. This represents the fact that the velocity of the ball changes due to gravity (velocity is a vector, so both the speed and angle of the ball's travel change).
- Add these vectors together, as shown above, to give a new vector. This new vector represents the velocity and displacement of the ball over the second second.
- Repeat this process until the ball hits something (draw the ground, if in doubt).
Questions
1. Which of the following are vectors?
- 20 cm
- 9.81 ms−2 towards the centre of the earth
- 5 km south-east
- 500 ms−1 on a bearing of 285.3°
2. A displacement vector a is the resultant vector of two other vectors, 5 m north and 10 m south-east. What does a equal, as a displacement and a bearing?
3. If I travel at a velocity of 10 ms−1 on a bearing of 030°, at what velocity am I travelling north and east?
4. An alternative method of writing vectors is in a column, as follows:
,
where x and y are the vertical and horizontal components of the vector respectively. Express |a| and the angle between a and in terms of x and y.
5. A more accurate method of modelling the trajectory of a ball is to include air resistance as a constant force F. How would this be achieved?
Graphs
There are two types of graphs of motion you need to be able to use and understand: distance-time graphs and velocity-time graphs.
Distance-time Graphs

A distance-time graph plots the distance of an object away from a certain point, with time on the x-axis and distance on the y-axis.There are several types of graphs of motion you need to be able to use and understand: distance-time graphs, position-time graphs, and velocity-time graphs.
Position-time Graphs or Displacement - Time Graphs
Distance-Time Graphs give you speed, but speed is never negative so you can only have a positive slope in a distance-time graph. Position-Time graphs show displacement, have direction, and from which you can calculate velocity. If we were to imagine the line on the position-time graph to the right as a function f(t), giving an equation for s = f(t), we could differentiate this to gain:
,
where s is displacement, and t is time. By finding f'(t) at any given time t, we can find the rate at which distance is increasing (or decreasing) with respect to t. This is the gradient of the line. A positive gradient means that distance is increasing, and a negative gradient means that distance is decreasing. A gradient of 0 means that the object is stationary. The velocity of the object is the rate of change of its displacement, which is the same as the gradient of the line on a distance-time graph. This is not necessarily the same as the average velocity of the object v:
Here, t and s are the total changes in displacement and time over a certain period - they do not tell you exactly what was happening at any given point in time.
Velocity-time Graphs

A velocity-time graph plots the velocity of an object, relative to a certain point, with time on the x-axis and velocity on the y-axis. We already know that velocity is the gradient (derivative) of the distance function. Since integration is the inverse process to differentiation, if we have a velocity-time graph and wish to know the distance travelled between two points in time, we can find the area under the graph between those two points in time. In general:
If
where v is velocity (in ms−1), t is time (in s), and s is the distance travelled (in m) between two points in time t1 and t2.
Also, by differentiation, we know that the gradient (or derivative of v = f(t)) is equal to the acceleration of the object at any given point in time (in ms−2) since:
Questions
1. In the following distance-time graph, what is the velocity 4 seconds after the beginning of the object's journey?

2a)Describe this person's movements.
2b)What is the velocity at 12 seconds?
3. In the following velocity-time graph, how far does the object travel between 7 and 9 seconds?
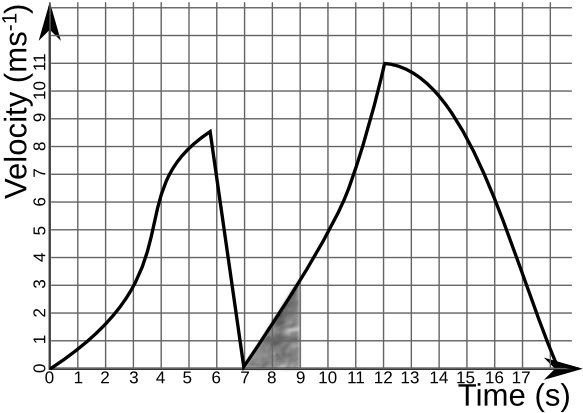
4. What is the object's acceleration at 8 seconds?
5. A car travels at 10ms−1 for 5 minutes in a straight line, and then returns to its original location over the next 4 minutes, travelling at a constant velocity. Draw a distance-time graph showing the distance the car has travelled from its original location.
6. Draw the velocity-time graph for the above situation.
The following question is more difficult than anything you will be given, but have a go anyway:
7. The velocity of a ball is related to the time since it was thrown by the equation . How far has the ball travelled after 2 seconds?
Kinematics
Kinematics is the study of how objects move. One needs to understand a situation in which an object changes speed, accelerating or decelerating, and travelling a certain distance. There are four equations you need to be able to use which relate these quantities.
Variables
Before we can understand the kinematic equations, we need to understand the variables involved. They are as follows:
- t is the length of the interval of time being considered, in seconds.
- v is the speed of the object at the end of the time interval, in ms−1.
- u is the speed of the object at the beginning of the time interval, in ms−1.
- a is the acceleration of the object during the time interval, in ms−2. Has to be a constant.
- s is the displacement (distance traveled) of the object during the time interval, in meters.
Equations
The four equations are as follows:
1.
2.
3.
4.
Derivations
It is also useful to know where the above equations come from. We know that acceleration is equal to change in speed per. unit time, so:
(*)
(1)
We also know that the average speed over the time interval is equal to displacement per. unit time, so:
(2)
If we substitute the value of v from equation 1 into equation 2, we get:
(3)
If we take the equation for acceleration (*), we can rearrange it to get:
If we substitute this equation for t into equation 2, we obtain:
(4)
Questions
1. A person accelerates from a speed of 1 ms−1 to 1.7 ms−1 in 25 seconds. How far has he travelled in this time?
2. A car accelerates at a rate of 18 kmh−2 to a speed of 60 kmh−1, travelling 1 km in the process. How fast was the car travelling before it travelled this distance?
3. A goose in flight is travelling at 4 ms−1. It accelerates at a rate of 1.5 ms−2 for 7 seconds. What is its new speed?
4. How far does an aeroplane travel if it accelerates from 400 kmh−1 at a rate of 40 kmh−2 for 1 hour?
Forces and Power
Forces
Forces are vectors. When solving problems involving forces, it is best to think of them as lots of people pulling ropes attached to an object. The forces are all pulling in different directions, with different magnitudes, but the effect is in only one direction, with only one magnitude. So, you have to add the forces up as vectors.
Forces cause things to happen. They cause an object to accelerate in the same direction as the force. In other words, forces cause objects to move in a direction closer to the direction they are pulling in. If the object is already moving, then they will not cause it to move in the direction of the force, as forces do not create velocities: they create accelerations.
If a force is acting on an object, it seems logical that the object will not accelerate as much as a result of the force if it has a lower mass. This gives rise to the equation:
,
where F = force applied (in Newtons, denoted N), m = mass (in kg) and a = acceleration (in ms−2). If we rearrange the equation, it makes more sense:
In other words, the acceleration in a given direction as the result of a force is equal to the force applied per. unit mass in that direction.
Work Done
You should already know how to calculate some types of energy, for example:
The amount of energy converted by a force is equal to the work done, which is equal (as you already know) to the force multiplied by the distance the object it is acting on moves:
When answering questions about work done, you may be given a force acting in a direction other than that of the displacement. In this case, you will have to find the displacement in the direction of the force, as shown in the section on Vectors.
Power
Power is the rate of change of energy. It is the amount of energy converted per. unit time, and is measured in Js−1:
,
where E = energy (in J) and t = time (in s). Since ΔE = work done, power is the rate at which work is done. Since:
,
where P = power (in Watts, denoted W), F = force and v = velocity.
Gravity
Gravity is something of a special case. The acceleration due to gravity is denoted g, and is equal to 9.81359ms−2. It is uniform over small distances from the Earth. The force due to gravity is equal to mg, since F = ma. Therefore:
Therefore, when things are dropped, they all fall at the same acceleration, regardless of mass. Also, the acceleration due to gravity (in ms−2) is equal to the gravitational field strength (in Nkg−1).
Questions
1. I hit a ball of mass 5g with a cue on a billiards table with a force of 20N. If friction opposes me with a force of 14.2N, what is the resultant acceleration of the ball away from the cue?
2. A 10g ball rolls down a 1.2m high slope, and leaves it with a velocity of 4ms−1. How much work is done by friction?
3. An electric train is powered on a 30kV power supply, where the current is 100A. The train is travelling at 90 kmh−1. What is the net force exerted on it in a forwards direction?
(incorporating Energy and Work Done)
A2 Exams
=
Rise and Fall of the Clockwork Universe
=
=
Field and Particle Pictures
=
=
Advances in Physics
=
| A reader requests expansion of this page to include more material. You can help by adding new material (learn how) or ask for assistance in the reading room. |