A-level Physics/Forces, Fields and Energy/Gravitational fields
We have already met gravitational fields, where the gravitational field strength of a planet multiplied by an objects mass gives us the weight of that object, and that the gravitational field strength, of Earth is equal to the acceleration of free fall at its surface, . We will now consider gravitational fields that are not uniform and how to calculate the value of for any given mass.
Gravity as a field of force
[edit | edit source]The effects of the Earth's gravity extend far out into space. For example, the Moon is kept in orbit by the Earth even though it is 400,000 km away (where gravity is the centripetal force). The Earth has a gravitational field that will attract any object with mass towards the centre of the planet.
Radial Fields
[edit | edit source]
Gravitational field is a region surrounding the earth in which another object feels force of attraction. Direction of this force is towards centre of the earth, or the center of the mass in general. Further objects feel less force attraction whereas closer objects feel more force of attraction.
Uniform fields
[edit | edit source]

A uniform field, however, has the lines perfectly parallel. The Earth's gravitational field can be considered to be uniform on the scale of small things such as cars, balls, and planes. For small heights at this scale (a few dozen kilometres), the strength of the field doesn't change enough to be noticeable. Again, the arrows point towards the centre of the Earth, since that is the way objects fall.
Newton's ideas of gravity
[edit | edit source]Isaac Newton was trying to find a way to explain why objects fell towards the centre of the Earth instead of simply staying put. He began to link the falling of an apple, with the "falling" of the Moon towards the Earth, and came up with his law of gravitation.
He suggested that any two objects with a mass would have a force of attraction between them. This force of attraction would be proportional to their masses, so that larger masses would have a stronger force of attraction than a smaller mass.
The gravitational field of every object is a radial field, since the mass is concentrated at the objects centre, and as you already know, this is the point at which gravity could be said to act.
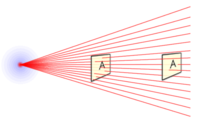
The strength of a radial field decreases as you move further away from it. As you can see on the diagram on the right, the number of field lines going through the plane quarter when the distance is doubled, and it will be of the original value if the distance was tripled.
This is called the inverse square law, and is true for anything which is a point source, such a light from a point or the amount of radiation emitted.
The inverse square law follows .
Using the above, Newton suggested that the force of attraction was proportional to the two masses as well as the distance between them:
- .
This relationship is the basis of how Newton's law of gravitation is often stated:
However, to make this into an equation, we need to add in a constant of proportionality, G:
- .
Where G is the gravitational constant, . There is also a minus sign in the equation, which will be explained in the "electric fields" module, where we will encounter repelling as well as attracting forces.
is also sometimes written as , so that capital M represents a large mass such a planet, and lower case m represents a small mass such as a ball or an aeroplane.
Gravitational field strength
[edit | edit source]Defining the gravitational field strength
[edit | edit source]The gravitational field strength tells us how strong a gravitational field is. You may recall that the gravitational field strength of the Earth near its surface is . This means an object that is near the surface of the earth will accelerate towards it at . We could then define the gravitational field strength as the acceleration an object will experience within that gravitational field.
A better definition, however, can be derived from the equation, . Making the subject of this gives us , or . From this arrangement of the equation, our definition of gravitational field strength now becomes:
The gravitational field strength at a point is the gravitational force exerted per unit mass placed at that point.
This means that the gravitational field strength, is equal to the force experienced by a mass of 1 kg in that gravitational field.
From the new definition, it follows that gravitational field strength is measured in , though it is perfectly acceptable to use for situations where it is treated as an acceleration (such as the acceleration of an object in free fall).
Finding the field strength of a mass
[edit | edit source]Since and , they can be combined to give:
- (by substituting F for mg)
- (by cancelling the lower case 'm's)
You can use this to find the gravitational field strength of a mass at a particular point, r.
Note that the gravitational field strength of the Earth near its surface is numerically equal to the acceleration of free fall, .
| A reader requests expansion of this page to include more material. You can help by adding new material (learn how) or ask for assistance in the reading room. |



















