Sorting algorithms
| Class | sorting algorithm |
|---|---|
| Data structure | Array |
| Worst case performance | О(n2) |
| Best case performance | O(n) |
| Average case performance | О(n2) |
| Worst case space complexity | О(n) total, O(1) auxiliary |
Bubble Sort
[edit | edit source]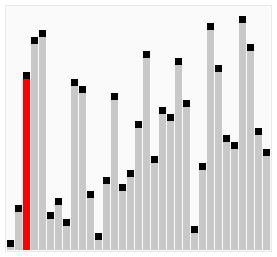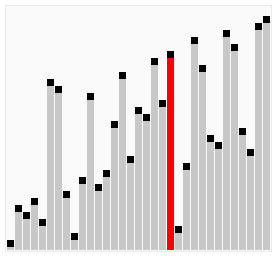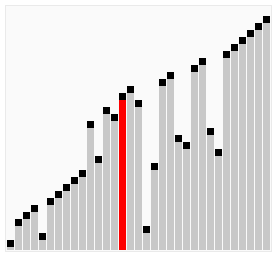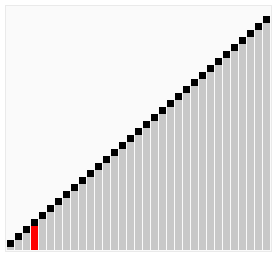
Bubble sort is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted. The algorithm gets its name from the way larger elements "bubble" to the top of the list. It is a very slow way of sorting data and rarely used in industry. There are much faster sorting algorithms out there such as insertion sort and quick sort which you will meet in A2.

Step-by-step example
[edit | edit source]Let us take the array of numbers "5 1 4 2 8", and sort the array from lowest number to greatest number using bubble sort algorithm. In each step, elements written in bold are being compared.
First Pass:
( 5 1 4 2 8 ) ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps them since 5 > 1
( 1 5 4 2 8 ) ( 1 4 5 2 8 ), It then compares the second and third items and swaps them since 5 > 4
( 1 4 5 2 8 ) ( 1 4 2 5 8 ), Swap since 5 > 2
( 1 4 2 5 8 ) ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.
The algorithm has reached the end of the list of numbers and the largest number, 8, has bubbled to the top. It now starts again.
Second Pass:
( 1 4 2 5 8 ) ( 1 4 2 5 8 ), no swap needed
( 1 4 2 5 8 ) ( 1 2 4 5 8 ), Swap since 4 > 2
( 1 2 4 5 8 ) ( 1 2 4 5 8 ), no swap needed
( 1 2 4 5 8 ) ( 1 2 4 5 8 ), no swap needed
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
Third Pass:
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
Finally, the array is sorted, and the algorithm can terminate.
Pseudocode implementation
[edit | edit source]The algorithm can be expressed as:
A[i] '''then'''
swap( A[i-1], A[i] )
swapped = true
'''end if'''
'''end for'''
'''while''' swapped
'''end procedure'''
</syntxhighlight>
{{CPTExercise|title=Exercise: Bubble Sort}}
We will now look at an example in Visual Basic using an array of people's heights. The following data set is being passed:
{| class="wikitable"
|-
! colspan="2" | height
|-
| 1 || 98
|-
| 2 || 12
|-
| 3 || 99
|-
| 4 || 54
|}
<syntaxhighlight lang="vbnet">
Sub bubbleSort(ByRef height() As integer)
Dim swapped As Boolean
Dim temp As integer
'sort the elements
Do
swapped = False
For Count = 1 To MaxSize - 1
If height(Count + 1) < height(Count) Then
temp = height(Count)
height(Count) = height(Count + 1)
height(Count + 1) = temp
swapped = True
End If
Next
Loop Until swapped = False
'Print out the elements
For Count = 1 To MaxSize
Console.WriteLine(Count & ": " & height(Count))
Next
End SubConstruct a trace table for the above code:
| Swapped | Count | MaxSize | Temp | height | |||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||
| False | 4 | null | 98 | 12 | 99 | 54 | |
Answer:
| Swapped | Count | MaxSize | Temp | height | |||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||
| False | 4 | null | 98 | 12 | 99 | 54 | |
| True | 1 | 98 | 12 | 98 | |||
| 2 | |||||||
| True | 3 | 99 | 54 | 99 | |||
| False | 1 | ||||||
| True | 2 | 98 | 54 | 98 | 99 | ||
| 3 | |||||||
| False | 1 | ||||||
| 2 | |||||||
| 3 | |||||||
Answer:
1: 12
2: 54
3: 98
4: 99
Show the following lists after one pass of bubble sort:
Sort into alphabetical order:
Henry, Cat, George, Mouse
Answer:
Cat, George, Henry, Mouse
Sort into alphabetical order:
G, C, N, A, P, CAnswer:
C, G, A, N, C, P
Sort into numerical order:
12, 56, 0, 23, 10Answer:
12, 0, 23, 10, 56
Show the following after 2 passes
Sort into alphabetical order:
Emu, Shrike, Gull, Badger
Answer:
Emu, Gull, Badger, Shrike (Pass 1) Emu, Badger, Gull, Shrike (Pass 2)
Sort into numerical order:
99, 45, 32, 56, 12
Answer:
45, 32, 56, 12, 99 (Pass 1) 32, 45, 12, 56, 99 (Pass 2)
Let's look at a more complicated example, an array of structures, TopScores. The following data set is being passed:
| TopScores | ||
|---|---|---|
| Name | Score | |
| 1 | Michael | 45 |
| 2 | Dave | 78 |
| 3 | Gerald | 23 |
| 4 | Colin | 75 |
Sub bubbleSort(ByRef TopScores() As TTopScore)
Dim swapped As Boolean
Dim temp As TTopScore
'sort the elements
Do
swapped = False
For Count = 1 To MaxSize - 1
If TopScores(Count + 1).Score > TopScores(Count).Score Then
temp.Name = TopScores(Count).Name
temp.Score = TopScores(Count).Score
TopScores(Count).Score = TopScores(Count + 1).Score
TopScores(Count).Name = TopScores(Count + 1).Name
TopScores(Count + 1).Name = temp.Name
TopScores(Count + 1).Score = temp.Score
swapped = True
End If
Next
Loop Until swapped = False
'Print out the elements
For Count = 1 To MaxSize
Console.WriteLine(Count & ": " & TopScores(Count).Name & " " & TopScores(Count).Score)
Next
End Sub
|
Exercise: Bubble Sort (Harder) Draw a trace table to see if it works:
Answer:
The output should be: 1: Dave 78 2: Colin 75 3: Michael 45 4: Gerald 23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Insertion Sort
[edit | edit source]
Unfortunately bubble sort is a very slow way of sorting data and very rarely used in industry. We'll now look at a much faster algorithm, insertion sort.
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array (or list) is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort and you may cover these at university. However, insertion sort provides several advantages:
- simple implementation
- efficient on small data sets
- uses a fixed amount of memory when running
Insertion sort requires the use of two arrays, one ordered, and one unordered. Each repetition of the algorithm moves an item from the unordered list, into a sorted position in the ordered list, until there are no elements left in the unordered list.
Sorting is typically done in-place without needing extra memory. The resulting array after k iterations has the property where the first k + 1 entries are sorted. In each iteration the first remaining entry of the input is removed, inserted into the result at the correct position, thus extending the result:
becomes
with each element greater than x copied to the right as it is compared against x.
|
Example: Insertion Sort The following table shows the steps for sorting the sequence {5, 7, 0, 3, 4, 2, 6, 1}. For each iteration, the number of positions the inserted element has moved is shown in parentheses. Altogether this amounts to 17 steps. 5 7 0 3 4 2 6 1 (0)
0 5 7 3 4 2 6 1 (2) 0 3 5 7 4 2 6 1 (2) 0 3 4 5 7 2 6 1 (2) 0 2 3 4 5 7 6 1 (4) 0 2 3 4 5 6 7 1 (1) 0 1 2 3 4 5 6 7 (6) for i ← 1 to i ← length(A)-1
{
// A[ i ] is added in the sorted sequence A[0, .. i-1]
// save A[i] to make a hole at index iHole
item ← A[i]
iHole ← i
// keep moving the hole to next smaller index until A[iHole - 1] is <= item
while iHole > 0 and A[iHole - 1] > item
{
// move hole to next smaller index
A[iHole] ← A[iHole - 1]
iHole ← iHole - 1
}
// put item in the hole
A[iHole] ← item
}
' a procedure to sort an array of integers
|
|
Exercise: Insertion Sort Describe the process of insertion sort Answer:
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array (or list) is built one entry at a time.
Show the how insert sort would work on the following unordered array: 9 6 7 1 2 Answer: sort left hand side is underlined 9 6 7 1 2 6 9 7 1 2 6 7 9 1 2 1 6 7 9 2 1 2 6 7 9 Show how the insert sort would work on the following unordered array G K L A J Answer: sort left hand side is underlined G K L A J G K L A J G K L A J A G K L J A G J K L Complete the trace table for the following code: Answer: |


