Materials in Electronics/Confined Particles/1D Infinite Wells
The 1D Infinite Well
[edit | edit source]Often, it is convenient to consider an electron "trapped" in a closed space, for example in a piece of semiconductor with a large bandgap between it and its surroundings. This kind of electron trap is called a 'potential well. The theoretically most straightforward case is the infinite potential well in one dimension, where an electron is confined completely and can never escape, as to do so would require an infinite amount of energy.
We will later expand this to more dimensions and the more realistic finite potential well, where the electron can escape.

For now, consider an electron trapped in an infinite potential well, of width L (right). The potential of this systems is given by:
The probability of finding an electron outside this region is zero. As the wavefunction of the electron in this well must be continuous according to the conditions on the wavefuction, we are seeking a solution to ψ(x) that is zero at x=0 and x=L. if this were not true, we would have a discontinuity here.
Solving for the Wavefunction
[edit | edit source]We need to solve Schrödingers Equation to find ψ(x):
.
Since V(x) is zero on this interval, we can write:
- .
Rearranging,
Recall that the energy is given by
Substituting for E in our differential equation gives:
This is now a second-order differential equation with a standard form. The general solution is given by:
[General Solution]
Applying Boundary Conditions
[edit | edit source]Applying the first boundary condition :
Therefore, B=0.
Applying the second boundary condition :
Therefore, kL must be a multiple of π:
We call A the normalisation coefficient, ψ0. This exists to ensure the probability of finding an electron in all of space is 1. Also, since when n=0 the whole equation goes to zero, the probability of an electron existing is zero, and thus, the solutions to the Schrödinger Equation for a particle in a 1D box start at n=1:
Because we a working in the x-direction, we have called our indexing number nx. This is called the wavenumber. The energies associated with the above solutions are given by:
There are two thing to note here.
- A wavefunction solving the Schrödinger Equation exists only for integer wavenumbers, n.
- Each wavefunction (eigenfunction) has a specific energy (eigenvalue) associated with it. This is proportional to the square of the wavenumber and the energy of the wavefunction with n=1, E1.
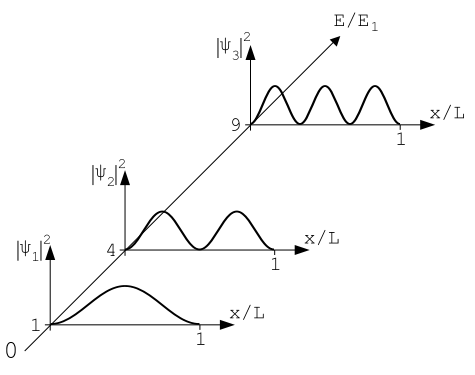
The diagram below shows the wavefunctions with wavenumbers 1, 2 and 3, plotted against the associated energy relative to E1:

The probability densities can be found easily once the wavefunctions have been found - simply take the modulus (in the case of complex wavefunctions) and square. This results in probability densities as shown below:
Normalisation Coefficient
[edit | edit source]We can find the normalisation coefficient, ψ0 using the knowledge that the electron must be somewhere in the quantum well, and therefore the area under the probability density function is one:
So, for our wavefunction, ,
Because the area under the sine curve over a whole number of periods in zero, we have
It turns out that this is independent of the wavenumber, so our normalised wavefunction for an electron in a 1-D infinite potential well is zero outside the well and given by the equation:
[Wavefunction of Particle 1D Infinite Potential Well]
Inside it, the associated energies are given by:
[Associated Energies of Wavefunctions]























![{\displaystyle \psi _{0}^{2}\left[\int \limits _{0}^{L}{{\frac {1}{2}}dx}-{\frac {1}{2}}\int \limits _{0}^{L}{\cos \left({\frac {2n_{x}\pi }{L}}x\right)dx}\right]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb685f2f0dd245b8e8120f84971b68d5a4e1e0ca)
![{\displaystyle \psi _{0}^{2}\left[{\frac {L}{2}}-{\frac {L}{4n_{x}\pi }}\left[\sin \left({\frac {2n_{x}\pi }{L}}x\right)\right]_{0}^{L}\right]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f38cf80077e7514eb1b06b4bf96417c4ca0a447)



