Engineering Acoustics/Transducers - Loudspeaker
Acoustic transducer[edit | edit source]
The purpose of an acoustic transducer is to convert electrical energy into acoustic energy. Many variations of acoustic transducers exist, such as electrostatic, balanced armature and moving-coil loudspeakers. This article focuses on moving-coil loudspeakers since they are the most commonly used type of acoustic transducer. First, the physical construction and principle of a typical moving coil transducer are discussed briefly. Second, electro-mechano-acoustical modeling of each element composing the loudspeaker is presented in a tutorial way to reinforce and supplement the theory on electro-mechanical analogies and electro-acoustic analogies previously seen in other sections. Third, the equivalent circuit is analyzed to introduce the theory behind Thiele-Small parameters, which are very useful when designing loudspeaker enclosures. A method to experimentally determine Thiele-Small parameters is also included.
Moving-coil loudspeaker construction and principle[edit | edit source]
The classic moving-coil loudspeaker driver can be divided into three key components:
1) The magnet motor drive system, comprising the permanent magnet, the center pole and the voice coil acting together to produce a mechanical force on the diaphragm from an electrical current.
2) The loudspeaker cone system, comprising the diaphragm and dust cap, permitting mechanical force to be translated into acoustic pressure;
3) The loudspeaker suspension, comprising the spider and surround, preventing the diaphragm from breaking due to over excursion, allowing only translational movement and tending to bring the diaphragm back to its rest position.
The following illustration shows a cut-away view of a typical moving coil-permanent magnet loudspeaker. A coil is mechanically coupled to a diaphragm, also called cone, and rests in a fixed magnetic field produced by a magnet. When an electrical current flows through the coil, a corresponding magnetic field is emitted, interacting with the fixed field of the magnet and thus applying a force to the coil, pushing it away or towards the magnet. Since the cone is mechanically coupled to the coil, it will push or pull the air it is facing, causing pressure changes and emitting a sound wave.

An equivalent circuit can be obtained to model the loudspeaker as a lumped system. This circuit can be used to drive the design of a complete loudspeaker system, including an enclosure and sometimes even an amplifier that is matched to the properties of the driver. The following section shows how such an equivalent circuit can be obtained.
Electro-mechano-acoustical equivalent circuit[edit | edit source]
Electro-mechanico-acoustical systems such as loudspeakers can be modeled as equivalent electrical circuits as long as each element moves as a whole. This is usually the case at low frequencies or at frequencies where the dimensions of the system are small compared to the wavelength of interest. To obtain a complete model of the loudspeaker, the interactions and properties of electrical, mechanical, and acoustical subsystems composing the loudspeaker driver must each be modeled. The following sections detail how the circuit may be obtained starting with the amplifier and ending with the acoustical load presented by air. A similar development can be found in [1] or [2].
Electrical subsystem[edit | edit source]
The electrical part of the system is composed of a driving amplifier and a voice coil. Most amplifiers can be approximated as a perfect voltage source in series with the amplifier output impedance. The voice coil exhibits an inductance and a resistance that may be directly modeled as a circuit.

Electrical to mechanical subsystem[edit | edit source]
When the loudspeaker is fed an electrical signal, the voice coil and magnet convert current to force. Similarly, voltage is related to the velocity. This relationship between the electrical side and the mechanical side can be modeled by a transformer.
;

Mechanical subsystem[edit | edit source]
In a first approximation, a moving coil loudspeaker may be thought of as a mass-spring system where the diaphragm and the voice coil constitute the mass and the spider and surround constitute the spring element. Losses in the suspension can be modeled as a resistor.

The equation of motion gives us :
Which yields the mechanical impedance type analogy in the form of a series RLC circuit. A parallel RLC circuit may also be obtained to get the mobility analog following mathematical manipulation:
Which expresses the mechanical mobility type analogy in the form of a parallel RLC circuit where the denominator elements are respectively a parallel conductance, inductance, and compliance.
Mechanical to acoustical subsystem[edit | edit source]
A loudspeaker’s diaphragm may be thought of as a piston that pushes and pulls on the air facing it, converting mechanical force and velocity into acoustic pressure and volume velocity. The equations are as follow:
;
These equations can be modeled by a transformer.
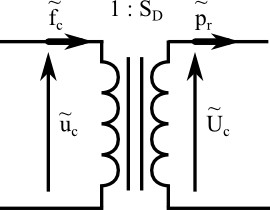
Acoustical subsystem[edit | edit source]
The impedance presented by the air load on the loudspeaker's diaphragm is both resistive due to sound radiation and reactive due to the air mass that is being pushed radially but does not contribute to sound radiation to the far field. The air load on the diaphragm can be modeled as an impedance or an admittance. Specific values and approximations can be found in [1], [2] or [3]. Note that the air load depends on the mounting conditions of the loudspeaker. If the loudspeaker is mounted in a baffle, the air load will be the same on each side of the diaphragm. Then, if the air load on one side is in the admittance analogy, then the total air load is as both loads are in parallel.
Complete electro-mechano-acoustical equivalent circuit[edit | edit source]
Using electrical impedance, mechanical mobility and acoustical admittance yield the following equivalent circuit, modeling the entire loudspeaker drive unit.

This circuit can be reduced by substituting the transformers and connected loads by an equivalent loading that would present the same impedance as the loaded transformer. An example of this is shown on figure 7, where acoustical and electrical loads and sources have been "brought over" to the mechanical side.

The advantage of doing such manipulations is that we can then directly relate electrical measurements with elements in the circuit. This will later allow us to obtain values for the different components of the model and match this model to real loudspeaker drivers. We can further simplify this circuit by using Norton's theorem and converting the series electrical components and voltage source into an equivalent current source and parallel electrical components. Then, using a technique called the Dot method, presented in section Solution Methods: Electro-Mechanical Analogies, we can obtain a single loop series circuit which is the dual of the parallel circuit previously obtained with Norton's theorem. If we are mainly interested in the low frequency behavior of the loudspeaker, as should be the case when using lumped element modeling, we can neglect the effect of the voice coil inductance, which has an effect only at high frequencies. Furthermore, the air load impedance at low frequencies is mass-like and can be modeled by a simple inductance . This results in a simplified low frequency model equivalent circuit, shown of figure 8, which is easier to manipulate than the circuit of figure 7. Note that the analogy used for this circuit is of the impedance type.

Where if is the radius of the loudspeaker and , the density of air. Mass elements, in this case the mass of the diaphragm and voice coil and the air mass loading the diaphragm can be regrouped in a single element:
Thiele-Small Parameters[edit | edit source]
Theory[edit | edit source]
The complete low frequency behavior of a loudspeaker drive unit can be modeled with just six parameters, called Thiele-Small parameters. Most of these parameters result from algebraic manipulation of the equations of the circuit of figure 8. Loudspeaker driver manufacturers seldom provide electro-mechano-acoustical parameters directly and rather provide Thiele-Small parameters in datasheets, but conversion from one to the other is quite simple. The Thiele-Small parameters are as follow:
1. , the voice coil DC resistance;
2. , the electrical Q factor;
3. , the mechanical Q factor;
4. , the loudspeaker resonance frequency;
5. , the effective surface area of the diaphragm;
6. , the equivalent suspension volume: the volume of air that has the same acoustic compliance as the suspension of the loudspeaker driver.
These parameters can be related directly from the low frequency approximation circuit of figure 8, with and being explicit.
; ; ;
Where is the Bulk modulus of air. It follows that, if given Thiele-Small parameters, one can extract the values of each component of the circuit of figure 8 using the following equations :
; ; ; ; ;
Measurement[edit | edit source]
Many methods can be used to measure Thiele-Small parameters of drivers. Measurement of Thiele-Small parameters is sometimes necessary if a manufacturer does not provide them. Also, the actual Thiele-Small parameters of a given loudspeaker can differ from nominal values significantly. The method described in this section comes from [2]. Note that for this method, the loudspeaker is considered to be mounted in an infinite baffle. In practice, a baffle with a diameter of four times that of the loudspeaker is sufficient. Measurements without a baffle are also possible: the air mass loading will simply be halved and can be easily accounted for. The setup for this method includes an FFT analyzer or a mean to obtain an impedance curve. A signal generator of variable frequency and an AC meter can also be used.


Once the impedance curve of the loudspeaker is measured, and can be directly identified by looking at the low frequency asymptote of the impedance value and the center frequency of the resonance peak. If the frequencies where are identified as and , Q factors can be calculated.
can simply be approximated by , where is the radius of the loudspeaker driver. The last remaining Thiele-Small parameter, is slightly trickier to measure. The idea is to either increase mass or reduce compliance of the loudspeaker drive unit and note the shift in resonance frequency. If a known mass is added to the loudspeaker diaphragm, the new resonance frequency will be:
And the equivalent suspension volume may be obtained with:
Hence, all Thiele-Small parameters modeling the low frequency behavior of the loudspeaker drive unit can be obtained from a fairly simple setup. These parameters are of tremendous help in loudspeaker enclosure design.
Numerical example[edit | edit source]
This section presents a numerical example of obtaining Thiele-Small parameters from impedance curves. The impedance curves presented in this section have been obtained from simulations using nominal Thiele-Small parameters of a real woofer loudspeaker. Firsy, these Thiele-Small parameters have been transformed into an electro-mechano-acoustical circuit using the equation presented before. Second, the circuit was treated as a black box and the method to extract Thiele-Small parameters was used. The purpose of this simulation is to present the method, step by step, using realistic values so that the reader can get more familiar with the process, the magnitude of the values and with what to expect when performing such measurements.
For this simulation, a loudspeaker of radius is mounted on a baffle sufficiently large to act as an infinite baffle. Its impedance is obtained and plotted in figure 11, where important cursors have already been placed.

The low frequency asymptote is immediately identified as . The resonance is clear and centered at . The value of the impedance at this frequency is about . This yields , which occurs at and . With this information, we can compute some of the Thiele-Small parameters.
As a next step, a mass of is fixed to the loudspeaker diaphragm. This shifts the resonance frequency and yields a new impedance curve, as shown on figure 12.

Once all six Thiele-Small parameters have been obtained, it is possible to calculate values for the electro-mechano-acoustical circuit modeling elements of figure 6 or 7. From then, the design of an enclosure can start. This is discussed in application sections Sealed box subwoofer design and Bass reflex enclosure design.
References[edit | edit source]
[1] Kleiner, Mendel. Electroacoustics. CRC Press, 2013.
[2] Beranek, Leo L., and Tim Mellow. Acoustics: sound fields and transducers. Academic Press, 2012.
[3] Kinsler, Lawrence E., et al. Fundamentals of Acoustics, 4th Edition. Wiley-VCH, 1999.
[4] Small, Richard H. "Direct radiator loudspeaker system analysis." Journal of the Audio Engineering Society 20.5 (1972): 383-395.























































