Engineering Acoustics/Simple Oscillation

The Position Equation

This section shows how to form the equation describing the position of a mass on a spring.

For a simple oscillator consisting of a mass m attached to one end of a spring with a spring constant s, the restoring force, f, can be expressed by the equation

$f = -sx\,$

where x is the displacement of the mass from its rest position. Substituting the expression for f into the linear momentum equation,

$f = ma = m{d^2x \over dt^2}\,$

where a is the acceleration of the mass, we can get

$m\frac{d^2 x}{d t^2 }= -sx$

or,

$\frac{d^2 x}{d t^2} + \frac{s}{m}x = 0$

Note that the frequency of oscillation $\omega_0$ is given by

$\omega_0^2 = {s \over m}\,$

To solve the equation, we can assume

$x(t)=A e^{\lambda t} \,$

The force equation then becomes

$(\lambda^2+\omega_0^2)A e^{\lambda t} = 0,$

Giving the equation

$\lambda^2+\omega_0^2 = 0,$

Solving for $\lambda$

$\lambda = \pm j\omega_0\,$

This gives the equation of x to be

$x = C_1e^{j\omega_0 t}+C_2e^{-j\omega_0 t}\,$

Note that

$j = (-1)^{1/2}\,$

and that C₁ and C₂ are constants given by the initial conditions of the system

If the position of the mass at t = 0 is denoted as x₀, then

$C_1 + C_2 = x_0\,$

and if the velocity of the mass at t = 0 is denoted as u₀, then

$-j(u_0/\omega_0) = C_1 - C_2\,$

Solving the two boundary condition equations gives

$C_1 = \frac{1}{2}( x_0 - j( u_0 / \omega_0 ))$

$C_2 = \frac{1}{2}( x_0 + j( u_0 / \omega_0 ))$

The position is then given by

$x(t) = x_0 cos(\omega_0 t) + (u_0 /\omega_0 )sin(\omega_0 t)\,$

This equation can also be found by assuming that x is of the form

$x(t)=A_1 cos(\omega_0 t) + A_2 sin(\omega_0 t)\,$

And by applying the same initial conditions,

$A_1 = x_0\,$

$A_2 = \frac{u_0}{\omega_0}\,$

This gives rise to the same position equation

$x(t) = x_0 cos(\omega_0 t) + (u_0 /\omega_0 )sin(\omega_0 t)\,$

Back to Main page

Alternate Position Equation Forms

If A₁ and A₂ are of the form

$A_1 = A cos( \phi)\,$ $A_2 = A sin( \phi)\,$

Then the position equation can be written

$x(t) = Acos( \omega_0 t - \phi )\,$

By applying the initial conditions (x(0)=x₀, u(0)=u₀) it is found that

$x_0 = A cos(\phi)\,$

$\frac{u_0}{\omega_0} = A sin(\phi)\,$

If these two equations are squared and summed, then it is found that

$A = \sqrt{x_0^2 + (\frac{u_0}{\omega_0})^2}\,$

And if the difference of the same two equations is found, the result is that

$\phi = tan^{-1}(\frac{u_0}{x_0 \omega_0})\,$

The position equation can also be written as the Real part of the imaginary position equation

$\mathbf{Re} [x(t)] = x(t) = A cos(\omega_0 t - \phi)\,$

Due to euler's rule (e^jφ = cosφ + jsinφ), x(t) is of the form

$x(t) = A e^{j(\omega_0 t - \phi)}\,$

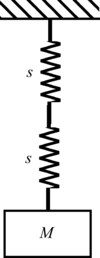
Example 1.1

GIVEN: Two springs of stiffness, $s$, and two bodies of mass, $M$

FIND: The natural frequencies of the systems sketched below

1. 

$s_{TOTAL} = s + s \text{ (springs are in parallel)}$

$\omega_{0} = \sqrt{\frac{s_{TOTAL}}{m_{TOTAL}}} = \sqrt{\frac{2s}{M}}$

$\mathbf{f_0} = \frac{\omega_{0}}{2\pi} = \mathbf{\frac{1}{2\pi}\sqrt{\frac{2s}{M}}}$

2. 

$\omega_{0} = \sqrt{\frac{s_{TOTAL}}{m_{TOTAL}}} = \sqrt{\frac{s}{2M}}$

$\mathbf{f_0} = \frac{\omega_{0}}{2\pi} = \mathbf{\frac{1}{2\pi}\sqrt{\frac{s}{2M}}}$

3. 

$\mathbf{1.}\text{ } s(x_1-x_2) = sx_2$

$\mathbf{2.}\text{ } -s(x_1-x_2) = m \frac{d^2x}{dt^2}$

$\frac{d^2x_1}{dt^2} + \frac{s}{2m}x_1 = 0$

$\omega_0 = \sqrt{\frac{s}{2m}}$

$\mathbf{f_0 = \frac{1}{2\pi}\sqrt{\frac{s}{2m}}}$

4. 

$\omega_0=\sqrt{\frac{2s}{m}}$

$\mathbf{f_0 = \frac{1}{2\pi}\sqrt{\frac{2s}{m}}}$

Back to Main page