Calculus/Limits/An Introduction to Limits
Limits, the first step into calculus, explain the complex nature of the subject. It is used to define the process of derivation and integration. It is also used in other circumstances to intuitively demonstrate the process of "approaching".
Introduction[edit | edit source]
Intuitive Look into Limits[edit | edit source]
The limit is one of the greatest tools in the hands of any mathematician. We will give the limit an approach. Because mathematics came only due to approaches... remember?!
We designate limit in the form:
This is read as "The limit of of as approaches ". This is an important thing to remember, it is basic notation which is accepted by the world.
We'll take up later the question of how we can determine whether a limit exists for at and, if so, what it is. For now, we'll look at it from an intuitive standpoint.
Let's say that the function that we're interested in is , and that we're interested in its limit as approaches . Using the above notation, we can write the limit that we're interested in as follows:
One way to try to evaluate what this limit is would be to choose values near 2, compute for each, and see what happens as they get closer to 2. There are two ways to approach values near 2. One is to approach from below, and the other is to approach from above:
| 1.7 | 1.8 | 1.9 | 1.95 | 1.99 | 1.999 | |
| 2.89 | 3.24 | 3.61 | 3.8025 | 3.9601 | 3.996001 |
The table above is the case from below.
| 2.3 | 2.2 | 2.1 | 2.05 | 2.01 | 2.001 | |
| 5.29 | 4.84 | 4.41 | 4.2025 | 4.0401 | 4.004001 |
The table above is the case from above.
We can see from the tables that as grows closer and closer to 2, seems to get closer and closer to 4, regardless of whether approaches 2 from above or from below. For this reason, we feel reasonably confident that the limit of as approaches 2 is 4, or, written in limit notation,
We could have also just substituted 2 into and evaluated: . However, this will not work with all limits.
Now let's look at another example. Suppose we're interested in the behavior of the function as approaches 2. Here's the limit in limit notation:
Just as before, we can compute function values as approaches 2 from below and from above. Here's a table, approaching from below:
| 1.7 | 1.8 | 1.9 | 1.95 | 1.99 | 1.999 | |
| -3.333 | -5 | -10 | -20 | -100 | -1000 |
And here from above:
| 2.3 | 2.2 | 2.1 | 2.05 | 2.01 | 2.001 | |
| 3.333 | 5 | 10 | 20 | 100 | 1000 |
In this case, the function doesn't seem to be approaching a single value as approaches 2, but instead becomes an extremely large positive or negative number (depending on the direction of approach). Well, one says such a limit does not exist because no finite number is approached. This arises the concept of infinity: an undefined quantity and the limit is also called infinite limit or limit without a bound.
Note that we cannot just substitute 2 into and evaluate as we could with the first example, since we would be dividing by 0.
Both of these examples may seem trivial, but consider the following function:
This function is the same as
Note that these functions are really completely identical; not just "almost the same," but actually, in terms of the definition of a function, completely the same; they give exactly the same output for every input.
In elementary algebra, a typical approach is to simply say that we can cancel the term , and then we have the function . However, that would be inaccurate; the function that we have now is not really the same as the one we started with, because it is defined when , and our original function was specifically not defined when . This may seem like a minor point, but from making this kind of assumptions we can easily derive absurd results, such that (see Mathematical Fallacy § All numbers equal all other numbers in Wikipedia for a complete example). Even without calculus we can avoid this error by stating that:
In calculus, we can introduce a more intuitive and also correct way of looking at this type of function. What we want is to be able to say that, although the function isn't defined when , it works almost as if it was. It may not get there, but it gets really, really close. For instance, . The only question that we have is: what do we mean by "close"?
Informal Definition of a Limit[edit | edit source]
As the precise definition of a limit is a bit technical, it is easier to start with an informal definition; we'll explain the formal definition later.
We suppose that a function is defined for near (but we do not require that it be defined when ).
We call the limit of as approaches if becomes close to when is close (but not equal) to , and if there is no other value with the same property.
When this holds we write
or
Notice that the definition of a limit is not concerned with the value of when (which may exist or may not). All we care about are the values of when is close to , on either the left or the right (i.e. less or greater).
Limit can also be understood as: is infinitely approaching to but never equals to , just like the function , which infinitely approaches to but never equals .
Basics[edit | edit source]
Rules and Identities[edit | edit source]
Now that we have defined, informally, what a limit is, we will list some rules that are useful for working with and computing limits. You will be able to prove all these once we formally define the fundamental concept of the limit of a function.
First, the constant rule states that if (that is, is constant for all ) then the limit as approaches must be equal to . In other words
Constant Rule for Limits
- If and are constants then .
- Example:
Second, the identity rule states that if (that is, just gives back whatever number you put in) then the limit of as approaches is equal to . That is,
Identity Rule for Limits
- If is a constant then .
- Example:
The next few rules tell us how, given the values of some limits, to compute others.
Operational Identities for Limits
Suppose that and and that is constant. Then
Notice that in the last rule we need to require that is not equal to 0 (otherwise we would be dividing by zero which is an undefined operation).
These rules are known as identities; they are the scalar product, sum, difference, product, and quotient rules for limits. (A scalar is a constant, and, when you multiply a function by a constant, we say that you are performing scalar multiplication.)
Using these rules we can deduce another. Namely, using the rule for products many times we get that
- for a positive integer .
This is called the power rule.
As a result, we can safely say that all limits for polynomial functions can be deduced into several limits that satisfy the identity rule and thus easier to compute.
- Example 1
Find the limit .
We need to simplify the problem, since we have no rules about this expression by itself. We know from the identity rule above that . By the power rule, . Lastly, by the scalar multiplication rule, we get .
- Example 2
Find the limit .
To do this informally, we split up the expression, once again, into its components. As above, .
Also and . Adding these together gives
- .
- Example 3
Find the limit .
From the previous example the limit of the numerator is . The limit of the denominator is
As the limit of the denominator is not equal to zero we can divide. This gives
- .
- Example 4
Find the limit .
We apply the same process here as we did in the previous set of examples;
- .
We can evaluate each of these; Thus, the answer is .
- Example 5
Find the limit .
In this example, evaluating the result directly will result in a division by 0. While you can determine the answer experimentally, a mathematical solution is possible as well.
First, the numerator is a polynomial that may be factored:
Now, you can divide both the numerator and denominator by :
Remember that the limit is a method to determine the approaching value of a function instead of the value of the function itself. So, though the function is undefined at , the value of the function is approaching to when
- Example 6
Find the limit .
To evaluate this seemingly complex limit, we will need to recall some sine and cosine identities (see Chapter 1.3). We will also have to use two new facts. First, if is a trigonometric function (that is, one of sine, cosine, tangent, cotangent, secant and cosecant functions), and is defined at , then .
Second, . This can be proved using squeeze theorem. Note that L'Hospital's rule is not allowed to be used to evaluate this limit because it causes circular reasoning,
in the sense that differentiating .requires this limit to equal one, which is exactly the equation that is being proven.
Method 1 (before learning L'Hôpital's rule):
To evaluate the limit, recognize that can be multiplied by to obtain which, by our trig identities, is . So, multiply the top and bottom by . (This is allowed because it is identical to multiplying by one.) This is a standard trick for evaluating limits of fractions; multiply the numerator and the denominator by a carefully chosen expression which will make the expression simplify somehow. In this case, we should end up with:
.
Our next step should be to break this up into by the product rule. As mentioned above, .
Next, .
Thus, by multiplying these two results, we obtain 0.
Note that we also cannot apply L'Hospital's rule to evaluate this limit because it causes circular reasoning.
We will now present an amazingly useful result, even though we cannot prove it yet. We can find the limit at of any polynomial or rational function, as long as that rational function is defined at (so we are not dividing by 0). That is, must be in the domain of the function.
If is a polynomial or rational function that is defined at then
We already learned this for trigonometric functions, so we see that it is easy to find limits of polynomial, rational or trigonometric functions wherever they are defined. In fact, this is true even for combinations of these functions; thus, for example, .
The Squeeze Theorem[edit | edit source]

The Squeeze Theorem is very important in calculus, where it is typically used to find the limit of a function by comparison with two other functions whose limits are known.
It is called the Squeeze Theorem because it refers to a function whose values are squeezed between the values of two other functions and , both of which have the same limit . If the value of is trapped between the values of the two functions and , the values of must also approach .
Expressed more precisely:
Suppose that holds for all in some open interval containing .
- If ,
- Then .

Example: Compute .
Since we know that
Multiplying into the inequality yields
Now we apply the squeeze theorem
Since ,
Finding Limits[edit | edit source]
Now, we will discuss how, in practice, to find limits. First, if the function can be built out of rational, trigonometric, logarithmic, or exponential functions, then if a number is in the domain of the function, then the limit at is simply the value of the function at :
when can be built out of rational, trigonometric, logarithmic, or exponential functions and the Domain of
If is not in the domain of the function, then in many cases (as with rational functions) the domain of the function includes all the points near , but not itself. An example would be if we wanted to find , where the domain includes all numbers besides 0.
In that case, in order to find we want to find a function similar to , except with the hole at filled in. The limits of and will be the same, as can be seen from the definition of a limit. By definition, the limit depends on only at the points where is close to but not equal to it, so the limit at does not depend on the value of the function at . Therefore, if , also. And since the domain of our new function includes , we can now (assuming is still built out of rational, trigonometric, logarithmic and exponential functions) just evaluate it at as before. Thus we have .
In our example, this is easy; canceling the 's gives , which equals at all points except 0. Thus, we have . In general, when computing limits of rational functions, it's a good idea to look for common factors in the numerator and denominator.
Specific DNE Situations[edit | edit source]
Note that the limit might not exist at all (DNE means "does not exist"). There are a number of ways in which this can occur:
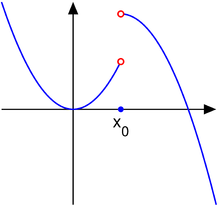
"Gap"
- does not exist when . There is no way to "approach" the middle of the graph. Note that the function also has no limit at the endpoints of the two curves generated (at and ). For the limit to exist, the point must be approachable from both the left and the right.
- Note also that there is no limit at a totally isolated point on a graph.
- "Jump"
- If the graph suddenly jumps to a different level, there is no limit at the point of the jump. For example, let be the greatest integer . Then, if is an integer, when approaches from the right , while when approaches from the left . Thus will not exist.

- Vertical asymptote
- In
- the graph gets arbitrarily high as it approaches 0, so there is no limit. (In this case we sometimes say the limit is infinite; see the next section.)

- Infinite oscillation
- These next two can be tricky to visualize. In this one, we mean that a graph continually rises above and falls below a horizontal line. In fact, it does this infinitely often as you approach a certain -value. This often means that there is no limit, as the graph never approaches a particular value. However, if the height (and depth) of each oscillation diminishes as the graph approaches the -value, so that the oscillations get arbitrarily smaller, then there might actually be a limit.
- The use of oscillation naturally calls to mind the trigonometric functions. An example of a trigonometric function that does not have a limit as approaches 0 is
- As gets closer to 0 the function keeps oscillating between and 1. In fact, oscillates an infinite number of times on the interval between 0 and any positive value of . The sine function is equal to 0 whenever , where is a positive integer. Between every two integers , goes back and forth between 0 and or 0 and 1. Hence, for every . In between consecutive pairs of these values, and , goes back and forth from 0, to either or 1 and back to 0. We may also observe that there are an infinite number of such pairs, and they are all between 0 and . There are a finite number of such pairs between any positive value of and , so there must be infinitely many between any positive value of and 0. From our reasoning we may conclude that, as approaches 0 from the right, the function does not approach any specific value. Thus, does not exist.
Determining Limits[edit | edit source]
The formal way to determine whether a limit exists is to find out whether the value of the limit is the same when approaching from below and above (see at the top of this chapter). The notation for the limit approaching from below (in increasing order) is
, notice the negative sign on the constant
The notation for the limit approaching from above (from decreasing order) is
, notice the positive sign on the constant
For example, let us find the limits of when is approaching in both directions. In other words, find and .
Recall the table we made when we are trying to intuitively feel the limit. We can use that to help us. However, if familiar enough with reciprocal functions, we can simply determine the two values by imagining the graph of the function. The following table is when is approaching from below.
| -0.3 | -0.2 | -0.1 | -0.05 | -0.01 | -0.001 | |
| -3.333 | -5 | -10 | -20 | -100 | -1000 |
Thus, we found that when is approaching from below to , the function approaches negative infinity. In mathematical terms:
Now let's talk about the approach from above.
| 0.3 | 0.2 | 0.1 | 0.05 | 0.01 | 0.001 | |
| 3.333 | 5 | 10 | 20 | 100 | 1000 |
We found that
The method of determining if limits exist is relatively intuitive. It only requires some practice to be familiar with the process.
If , then . If , then the limit does not exist (DNE).
Let's use the same example: find .
Since we already found that and , and obviously,
We can say that does not exist.
Infinity Situations[edit | edit source]
Now consider the function
What is the limit as approaches zero? The value of does not exist; it is not defined.
Notice, also, that we can make as large as we like, by choosing a small , as long as . For example, to make equal to , we choose to be . Thus, does not exist.
However, we do know something about what happens to when gets close to 0 without reaching it. We want to say we can make arbitrarily large (as large as we like) by taking to be sufficiently close to 0, but not equal to 0. We express this symbolically as follows:
Note that the limit does not exist at ; for a limit, being is a special kind of not existing. In general, we make the following definition.
We say the limit of as approaches is infinity if becomes very big (as big as we like) when is close (but not equal) to .
In this case we write
or
- .
Similarly, we say the limit of as approaches is negative infinity if becomes very negative when is close (but not equal) to .
In this case we write
or
- .
An example of the second half of the definition would be that .
Applications of Limits[edit | edit source]
To see the power of the concept of the limit, let's consider a moving car. Suppose we have a car whose position is linear with respect to time (that is, a graph plotting the position with respect to time will show a straight line). We want to find the velocity. This is easy to do from algebra; we just take the slope, and that's our velocity.
But unfortunately, things in the real world don't always travel in nice straight lines. Cars speed up, slow down, and generally behave in ways that make it difficult to calculate their velocities.
Now what we really want to do is to find the velocity at a given moment (the instantaneous velocity). The trouble is that in order to find the velocity we need two points, while at any given time, we only have one point. We can, of course, always find the average speed of the car, given two points in time, but we want to find the speed of the car at one precise moment.
This is the basic trick of differential calculus, the first of the two main subjects of this book. We take the average speed at two moments in time, and then make those two moments in time closer and closer together. We then see what the limit of the slope is as these two moments in time are closer and closer, and say that this limit is the slope at a single instant.
We will study this process in much greater depth later in the book. First, however, we will need to study limits more carefully.







































![{\displaystyle \lim _{x\to c}{\Big [}f(x)+g(x){\Big ]}=\lim _{x\to c}f(x)+\lim _{x\to c}g(x)=L+M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63558973f7dd0b0f40d8b5ec75c0069be55cbfd5)
![{\displaystyle \lim _{x\to c}{\Big [}f(x)-g(x){\Big ]}=\lim _{x\to c}f(x)-\lim _{x\to c}g(x)=L-M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2245bcbbf23e62d18e911d97fb3374f21029d253)
![{\displaystyle \lim _{x\to c}{\Big [}f(x)\cdot g(x){\Big ]}=\lim _{x\to c}f(x)\cdot \lim _{x\to c}g(x)=L\cdot M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bb3a49fa4c6cf42d9198a0a3a589f0d37f801ef)









![{\displaystyle \lim _{x\to 2}{\Big [}4x^{3}+5x+7{\Big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9aa0dd59f814b3b6360f3bf16731fe0ce310506)



![{\displaystyle \lim _{x\to 2}{\Big [}4x^{3}+5x+7{\Big ]}=\lim _{x\to 2}4x^{3}+\lim _{x\to 2}5x+\lim _{x\to 2}7=32+10+7=49}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89f353a2c991ed44a76cbe15ec92e1a7cef64b59)

![{\displaystyle \lim _{x\to 2}{\Big [}4x^{3}+5x+7{\Big ]}=49}](https://wikimedia.org/api/rest_v1/media/math/render/svg/353024d0a21d472b9fcc214957ec24ba2bba2071)
![{\displaystyle \lim _{x\to 2}(x-4)(x+10)=\lim _{x\to 2}{\big [}x-4{\big ]}\cdot \lim _{x\to 2}{\big [}x+10{\big ]}=(2-4)(2+10)=-24}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65c63b2f02d6f5fcce2f8d9f4a03197753b87877)


![{\displaystyle \lim _{x\to 4}{\frac {x^{4}-16x+7}{4x-5}}={\frac {\lim \limits _{x\to 4}{\Big [}x^{4}-16x+7{\Big ]}}{\lim \limits _{x\to 4}{\Big [}4x-5{\Big ]}}}={\frac {\lim \limits _{x\to 4}x^{4}-\lim \limits _{x\to 4}16x+\lim \limits _{x\to 4}7}{\lim \limits _{x\to 4}4x-\lim \limits _{x\to 4}5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7642ef2f4b9658fcf3b321603072b3855871b00c)







![{\displaystyle \lim _{x\to 0}\left[{\frac {1-\cos(x)}{x}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/439aaecbbba70015d6ba2bc0dbbdb28af2a4c879)







![{\displaystyle =\lim _{x\to 0}\left[{\frac {1-\cos(x)}{x}}\cdot {\frac {1}{1}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/004dae8cac61686c58224237354804a0103ebd9a)
![{\displaystyle =\lim _{x\to 0}\left[{\frac {1-\cos(x)}{x}}\cdot {\frac {1+\cos(x)}{1+\cos(x)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7224657c3fd7b37a16b7a5588b984dda8bc95b3)



![{\displaystyle =\lim _{x\to 0}\left[{\frac {\sin(x)}{x}}\cdot {\frac {\sin(x)}{1+\cos(x)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d41ba3366a2096441341036c51d162bec854de87)
![{\displaystyle \lim _{x\to 0}\left[{\frac {\sin(x)}{x}}\right]\cdot \lim _{x\to 0}\left[{\frac {\sin(x)}{1+\cos(x)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01925eba7f3f6d88a6cb8834c53788681d75b7a5)
![{\displaystyle \lim _{x\to 0}\left[{\frac {\sin(x)}{x}}\right]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/160f1b5c8451bba4f762d0423a4ddf0b4c06b44f)
![{\displaystyle \lim _{x\to 0}\left[{\frac {\sin(x)}{1+\cos(x)}}\right]={\frac {\lim \limits _{x\to 0}{\big [}\sin(x){\big ]}}{\lim \limits _{x\to 0}{\big [}1+\cos(x){\big ]}}}={\frac {0}{1+\cos(0)}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3162bb4a9f849e9fce9bed16c245dd028f15052a)

![{\displaystyle \lim _{x\to 1}{\bigg [}\sin(x^{2})+4\cos ^{3}(3x-1){\bigg ]}=\sin(1^{2})+4\cos ^{3}(3\cdot 1-1)=\sin 1+4\cos ^{3}2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57ef4597d5d1294ea634e4d530898e083ed19734)






























![{\displaystyle [-2,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f94b820404eca2a458cb2c7d8c24be85fffccf90)


![{\displaystyle (0,{\tfrac {1}{\pi }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f41cc2319c9c4acc7cd957eb6a02fc6070fa869a)



































