Basic Physics of Nuclear Medicine/X-Ray CT in Nuclear Medicine
The need for attenuation compensation in SPECT imaging has been understood for many years but it has only been in recent times that effective techniques have been applied in commercial systems. Gamma rays get attenuated by the medium through which they pass, as we've seen earlier, via photoelectric absorption and Compton scattering. The projections measured in SPECT imaging therefore contain impressions of this attenuation which reduce their fidelity for tomographic reconstruction, as illustrated in the following figure:

Patient specific attenuation maps can be used to correct the measured projections. These can be produced using the gamma camera to generate a transmission scan of the patient using a radioisotope source – see the following figure for an example:

The transmission scan contains the attenuation information for the volume of interest within the patient and a map of this attenuation pattern is subsequently applied to each SPECT projection prior to filtered back projection. A more powerful approach is to use an X-ray CT scanner to generate the attenuation maps – see the following figure. Numerous hybrid scanners have been produced as a result which combine nuclear medicine with CT imaging, as in SPECT/CT and PET/CT – see the following figure for an example:

An additional benefit of these developments is the simultaneous capability, with sufficient computing power, of blending the nuclear medicine and CT images so as to generate physiological images colocalized with images of patient anatomy – as shown in the following figure – and hence improve the diagnostic utility of nuclear medicine procedures.

Hybrid scanners generally have a single patient couch with the gamma camera gantry moulded to the front of a CT unit so that the patient can be transported into the X-ray beam before or after the SPECT acquisition. Some CT units are of a low resolution design and generate crude, single slice CT images which are sufficiently accurate for SPECT attenuation correction but are of insufficient quality on their own for diagnostic purposes – see the example below. There are also higher resolution CT units in use for hybrid scanning with capabilities of acquiring, for instance, 16-slice helical scans which can compete directly with the diagnostic capabilities of dedicated CT scanners.

This chapter provides an overview of the physical aspects of X-ray CT scanning from a nuclear medicine perspective. We begin with various scanner designs and will explore a number of computational techniques relevant to this form of imaging. The intention is to provide a foundation for understanding the application of X-ray CT in nuclear medicine.
Conventional Radiography[edit | edit source]
The attenuation of an X-ray beam in the body is used in conventional radiography to project a shadow onto an image receptor (as shown in the figure below). These shadowgraphs record a two-dimensional representation of a three-dimensional object. Small lesions are therefore not readily identified because of overlapping and underlying anatomy, image distortion occurs because of unequal magnification effects and low contrast masses are poorly delineated since scatter contributes substantially to the image data.

We can consider that there is a degeneracy introduced into such images, i.e. two anatomically quite different objects may produce the same film density because the effective attenuation they each produce is identical, as illustrated in the following figure:

Panel (a) shows a pencil beam of X-radiation of incident intensity, Io, attenuated by the body, represented here for simplicity by four volume elements each of thickness, Δx, and of different linear attenuation coefficients, μ1 thru μ4. The transmitted intensity, when no scattered radiation is detected, is given by I, which is dependent on the sum of these linear attenuation coefficients, according to the exponential attenuation equation. Panel (b) illustrates that two adjacent columns of volume elements can generate identical values of the transmitted intensity, I, even though the two columns contain volume elements with different linear attenuation coefficients. In other words, what is detected in the integrated contribution of the linear attenuation coefficients without any information about the contribution from any individual volume element.
One way to improve this situation is to use X-Ray Computed Tomography (CT). Note that the image reconstruction algorithms developed for X-ray CT can also be applied to gamma camera images (as in SPECT) to overcome limitations of planar nuclear imaging and to images generated using positron-emitting radioisotopes (as in PET).
Back Projection[edit | edit source]
We have considered this method of computerized image reconstruction in a previous chapter in the context of SPECT. Our intention here is to consider this reconstruction method in the context of X-Ray CT.
The following figure is a representation of how back projection works. The basic premise is that any attenuation of the X-ray beam is assumed to have occurred uniformly along the entire ray path.

Thus, the result of the back projection of the first profile, P1 is to put the values 7 and 9 in both elements of the first and second rows, respectively. The second profile, P2 adds a 4 to the top right element, 1 to the bottom left element and 11 to the other two elements when back projected. The other profiles are treated in similar fashion. Following subtraction of an offset (16 in this case) and renormalisation (division by 3 in this case) of the data set, the final image is obtained. You should confirm for yourself that this final matrix satisfies all projections.
The principle is demonstrated in more detail in the following figure:

A single profile is back projected to give a dark stripe across the entire image plane [panel (a)]. As we scan the phantom from many directions and back project the ray profiles onto the image plane [panel (b)], an image of the radio-dense dot, albeit a poor one, begins to resolve [panel (c)]. As the number of projections increases, the quality improves but some blurring will always remain in the image.
This blurring can be removed using what is known as Filtered Back Projection.
Filtered Back Projection[edit | edit source]
The blurring inherent in the simple back projection process can be suppressed mathematically using filtering techniques and the overall reconstruction process is then called Filtered Back Projection. In this technique (see the following figure), the attenuation profile is first filtered to counteract the effect of sudden density changes which cause the blurring in simple back projection. Note that the graphical representation in the figure is very crude as the filtered profile may be a quite complicated function of distance as illustrated in panel (c). The filter is also referred to as a convolution filter, or convolution kernel. After completion of the filtration process, the Inverse Fourier Transform is applied to the data for each profile before the back projection process is undertaken. Notice that the reconstructed image [panel (d)] is free of the star artefact generated in unfiltered back projection.

Most CT scanners offer a choice of filters which may be selected by the operator to enhance either soft tissue features or bone detail in images. Indeed, the image can be post-processed using a different filter after the scan has been completed if so desired. Images can be generated to enhance bone detail on the one hand and to observe subtle low contrast masses on the other, without the need to re-scan the patient. Thus, the filter choice will have a major impact on image quality. Two common filters used in X-ray CT are those due to Ramachandran & Lakshminarayanan (Ram-Lak) and to Shepp & Logan. In SPECT, Butterworth, Hanning and Metz are used, as you will remember. The ramp filter on its own compensates for artefacts introduced by the simple back projection process but does not compensate for the increasing noise content of the data with increasing spatial frequency. The Ram-Lak is a ramp filter which leaves all frequencies unchanged except those above a cut-off, which are eliminated. Most of the other filters suppress higher frequencies to varying degrees. Sometimes these filters are referred to as algorithms. The term kernel is also used. Images of an axial tomogram reconstructed with a soft tissue and with a bone algorithm are shown below as examples:

There's an excellent online CT reconstruction simulator available via the Biomedical Imaging Group at the EPFL. As an exercise, you might like to explore your understanding of filtered back projection by varying the type of filter used prior to reconstruction. You might also like to explore the influence of the number of angles used for profile acquisition on the quality of the reconstructed image.
CT Scanning Geometries[edit | edit source]

Most CT scanner designs use some form of mechanical gantry which allows movement of the X-ray tube and the detector around the patient. The X-ray beam was collimated to a pencil beam in early designs and consists of a wide fan beam in modern systems. The thickness of the slice, typically 1 to 10 mm, is generally defined by pre-patient collimation using motor driven adjustable wedges external to the X-ray tube. Even with relatively large fan beams the volume of tissue irradiated is still small quite compared with projection radiography and scatter is a less serious problem. The detectors have collimators placed in front of them to minimise the impact of out of slice scatter. To minimise the effects of beam hardening CT scanners use a heavily filtered beam (the Siemens Somatom Plus uses 2.7 mm Al plus 0.2 mm Cu, for instance) operating at 120 – 140 kVp. Note that even with the best radiographic geometry, such as in the third generation scanners, object magnification is substantial and the finite size of the focal spot, typically 1 mm, may well limit the achievable spatial resolution.
The first generation of CT scanner used what is referred to as Translate-Rotate geometry. The original EMI Mk 1 scanner (see the figure on the right), for instance, used a pencil X-ray beam and a single detector (a NaI:Tl scintillator coupled to a photomultiplier tube). During the translational motion of the gantry, the transmitted X-ray beam was sampled 160 times to produce a single profile. A rotation through 1 degree with the X-ray beam off then followed before a new profile was obtained. This procedure was completed until the patient's head was scanned from 180 different angles.

The whole procedure took about 5 minutes and depended on the patient remaining completely still. The patient's head was usually clamped to minimise patient motion. In addition, their head was surrounded by a water bag which helped to overcome problems associated with afterglow in the NaI(Tl) scintillator and the very substantial signal dynamic range that would otherwise be present at the detectors. Subsequent generations of scanners have sought to decrease the scan time to a few seconds to minimise the movement artifact.
The second generation of scanner addressed this issue by using a small fan beam (see the next figure) with multiple detectors – up to 30 in some designs. The detectors collect multiple data readings during a translation so that fewer translations and rotations are required. Each of the detectors collects its own limited profile during each translation. Typically, a rotation of 30 degrees was employed between translational movements so that only six rotational movements were required to obtain the data for one slice.
Scan times of between 5 to 90 seconds were achieved with this design. The detector elements were scintillators but the water bag was dispensed with and body scans could be performed for the first time. The use of multiple detectors gave a quantum leap in performance.
The third generation of CT scanner decreased scan times even further by using a Rotate-Rotate geometry (see the figure on the right). Most scanners today are of the third generation type. A typical machine employs a large fan beam such that the patient is completely encompassed by the fan. The number of detector elements is typically in the hundreds, e.g.
- the GE Hispeed Advantage has 852 elements 1.0 mm apart;
- the Siemens Somatom Plus 4 has 768 elements 1.1 mm apart; and
- the Toshiba Xpress/SX has 896 elements 1.03 mm apart.

The detector elements are aligned along the arc of a circle centred on the focus of the X-ray tube. The X-ray tube and detector array rotate as one through 360 degrees during which time several hundred discrete profiles are obtained. Both solid state detectors and pressurised xenon gas detectors are used for data acquisition.
Because the fan beam totally encompasses the patient, translational motion is not needed and the tube and detector array rotate as one about the patient. The number of profiles recorded depends on the chosen scan parameters but is at least a few hundred and can be in excess of a thousand. Scan times can be as low as a second. Although the dynamic range of the detectors is very high, some manufacturers control excessive variations in signal strength by using bow-tie shaped filters chosen to suit the body or head shape. Such filters generally attenuate the peripheral part of the fan beam to a greater extent than the central part. It also helps overcome the effects of beam hardening and to minimise patient skin dose in the peripheral part of the field of view.
A number of variants on this geometry have been developed, which include those based on offsetting the centre of rotation and the use of a flying focus X-ray tube.

The fourth generation of CT scanner uses a Rotate-Fixed Ring geometry where a ring of fixed detectors completely surrounds the patient. The X-ray tube rotates inside the detector ring through a full 360 degrees with a wide fan beam. Only those detectors which see the beam are activated at any one time which means that only a small fraction of thousands of detector elements (e.g. the Picker PQ-5000V has 4800 detector elements 1.1 mm apart) are in use at any given time. Scan time is comparable with third generation scanners but the radiographic geometry is poor because the X-ray tube must be closer to the patient than the detectors, i.e. the geometric magnification is large.
The disadvantages of poor geometry noted above has been alleviated very neatly by the so called nutating geometry. The X-ray tube is external to the detector ring but slightly out of the detector plane. Scan times as low as 0.6 s can be achieved using machines of this type with interscan delays of as little as 100 ms. Excellent resolution (0.35 mm) can be obtained by using as many several thousand detector elements.
Helical Scanning[edit | edit source]
Innovations in slip-ring technology, beginning with the Siemens Somatom Plus and the Toshiba TCT 900S, have enabled the X-ray tube to rotate continuously in the same direction which overcomes problems of interscan delays. When the continuous motion of the X-ray tube is combined with a continuous advance of the patient table along the axis of the scanner we have helical (also called spiral) scanning, as illustrated the following figure. Typical table velocities are 1 – 10 mm/s; a complete 360 degree rotation can be achieved in 0.5 s and the nominal fan beam thickness is 1 mm or greater.

In the context of helical scanning a parameter called pitch is defined as the:
In other words, for a couch advance of 10 mm and a nominal slice width of 10 mm, the pitch is 1. Pitch values are typically in the range of 1 to 2 depending on the required spatial resolution in the direction of the couch motion. Its a coverage indicator, in other words.
A significant reduction in scan times results from helical scanning because large volumes can be scanned contiguously without any gaps and with little influence from patient motion. The Somatom Plus-4A, for instance, allows up to 80 slices to be scanned contiguously in 60 seconds of non-stop scanning. Single breathhold scanning of the thorax is therefore possible and reconstruction, with minimal loss of spatial resolution, of sagittal and coronal planes is feasible.
Axial reconstruction in helical scanning is illustrated in the following figure. It is seen that no axial slices are actually irradiated during the scan and that any transaxial image data needs to be estimated from the acquired helical record. One estimation technique is referred to as z-interpolation, because it applies data interpolation techniques along the z-dimension of the acquired data, i.e. the patient's head-to-foot axis.

The filtered back projection reconstruction process is therefore modified to include an z-interpolation step prior to Fourier filtration, as illustrated in the following flow diagram:

Interpolation & Extrapolation[edit | edit source]
Before proceeding, let's briefly review the topic of interpolation and extrapolation to clarify our basic understanding and to put the subsequent discussion in context. Let's start with a simple one-dimensional case, as illustrated in the following graph. Suppose we've taken measurements A and B and plotted them on the graph, and wish to estimate the value at an in-between point, C. Such an estimation process is called interpolation, and if we assume that there's a linear relationship between variables X and Y as illustrated in our graph, the process of estimating point C is called linear interpolation. Other functions can also be used as interpolatants for more complex data than we're considering here.

If we also require knowledge about point D on our graph, i.e. a point outside the measured range, we refer to the estimation process as extrapolation, and linear extrapolation is illustrated in our graph above.
Mathematically we can write that given:
then the Y-value of point C is given by:
using linear interpolation. You might like to develop a similar equation as an exercise which can be used to determine the Y-value of point, D.
Since helical scanning is a three-dimensional phenomenon, we need to develop some two-dimensional perspectives on the situation before proceeding with our discussion – as illustrated in the following figure:

We'll use the side view in the following discussion.
Interpolation in Helical CT[edit | edit source]
A large number of computational methods have been developed for helical scanning. The 360o linear interpolation algorithm is illustrated in the following figure as an example:

The following equation can be developed on the basis of our earlier discussion for linear interpolation of the transaxial data of interest:
where:
- Pz(i, α) is the interpolated projection for an angle, α, at position Zref;
- Pj(i, α) is the helical projection measured in rotation j at position Zj and projection angle α;
- Pj+1(i, α) is the helical projection measured in rotation j+1 at position Zj+1 and projection angle α; and
This interpolation process is applied throughout all data points in the helix to generate estimates of the axial data, prior to filtered backprojection. Higher order interpolation is also possible where data points from, say, four rays are used in the estimation. In addition, sophisticated z-axis filters can be applied for these estimations in multi-slice CT.
Volume Imaging[edit | edit source]
It is possible to produce a number of slices per rotation when the fan beam of a CT scanner is broadened along the z-axis and two-dimensional detectors are used. The fan beam can be formed into the shape of a cone on this basis and concepts such as volume imaging and cone beam CT can be applied. Terms such as multi-slice and multi-detector CT can also be used in this context, although as you will see the second of these two terms is probably the more appropriate.
The 2-D detectors are solid-state devices and the simplest example is the Matrix Array, as illustrated below:

The array can consist of (say) 912 columns by 16 rows of identical detectors, each 1.25 mm square, curved to fit an arc of the x-ray tube rotation. Eight of these columns are shown in panel (a) above being irradiated by an X-ray beam of width 6 mm, with the implication that data for four 1.25 mm axial slices can be acquired simultaneously. More rows, up to sixteen in this case, can be irradiated simultaneously with this arrangement when the x-ray beam is broadened to encompass the width of the detector array.
Flexibility can be built into this design by coupling the outputs of adjacent detector rows, as illustrated in panels (b), (c) and (d), where the outputs of 2, 3 and 4 rows, respectively, are summed to simultaneously generate four 2.5 mm thick slices, or four 3.75 mm slices, or (you guessed it!) four 5 mm slices.
A more flexible design is provided by the Adaptive Array detector, as illustrated in the next figure:

Rather than columns of square detectors, this array uses columns of detectors of variable width, such that the width in the two central columns is relatively narrow, e.g. 1 mm as in the figure above, with the column width increasing towards the periphery, e.g. from 1.5 mm, through 2.5 mm to 5 mm as in our figure. The reason for this pattern is explained below.
Four modes of operation of this detector array are shown in the following figure:

We can see in panel (a) that two 0.5 mm slices can be acquired when a 1 mm thick fan beam is aligned with the central columns of the adaptive array. In panel (b) we can see that four 1 mm slices can be acquired using a fan beam of thickness 4 mm. Detector coupling is illustrated in panels (c) and (d), where the outputs of detectors in the four central columns are coupled so as to simulate two 2.5 mm wide detection columns and hence acquire data for four 2.5 mm slices. How do you think this coupling process is applied in panel (d) to generate four 5 mm slices?
A second advantage of the adaptive array is that the number of individual detector elements on each row can be considerably reduced, from 16 to 8 in the case we've just discussed. This adds greatly to the speed with which data can be generated by the array and reduces the number of computations necessary for uniformity and other corrections that must also be applied to the measured data.
The interpolation process in multi-slice helical CT is illustrated in our final figure where the situation in a 4-slice system using a 360o multi-slice filtered interpolation algorithm is shown:

The number of detector rows in Multi-Detector CT (MDCT) in 2010 is typically 8, 16 or 64, or greater – even a 320-slice scanner has been developed.
CT Image Display[edit | edit source]
After the computer calculates the linear attenuation coefficient for each pixel via filtered back projection, the values are normalised to the value for water as a reference, scaled and presented as a Hounsfield or CT-number which is defined as:
where μm and μwater are the linear attenuation coefficients for the tissue material and for water, respectively. The CT-number of water is therefore zero. CT-numbers for a number of tissues are shown in the following table:
| Tissue | CT-Number (H) |
|---|---|
| Lung | -300 |
| Fat | -90 |
| White Matter | 30 |
| Gray Matter | 40 |
| Muscle | 50 |
| Trabecular Bone | 300-500 |
| Cortical Bone | 600-3,000 |
The image is usually presented on a computer monitor using a grey scale. The grey scale is chosen to encompass all or some part of the entire range of CT-numbers by selecting a suitable window level and window width. The window width is the range of CT-numbers we select for display and the window level is, usually but not always, the central CT-number about which the window is chosen. Typically, the highest number is assigned to white and the lowest number to black with all intervening numbers assigned intensities on a linear scale. Thus, air will be displayed as black and cortical bone will appear relatively bright.
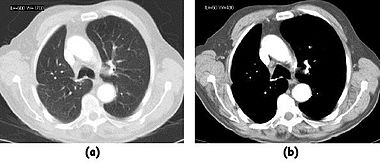
Examples of image display manipulation are shown in the following two figures. In the first, the same image of a slice through a patient's liver is displayed using a relatively narrow window (high contrast) and also with a wide window. The image with the narrower window appears noisier, but this is merely a reflection of the fact that the gray scale spreads over a narrow range of CT-numbers.

In the second figure, a relatively narrow window has been used to highlight pathology:
Scanned Projection Radiography[edit | edit source]
Most CT systems use scanned projection radiography (SPR), also known as a scout view and scanogram, to establish a consistent set of anatomical markers for all subsequent procedures. In SPR, the fan beam is not rotated about the patient but is fixed, and the patient couch is moved slowly through the beam. Each detector element measures a varying amount of radiation intensity as the anatomy changes between the focus and the detector. These discrete detector signals are digitised but not processed to any great extent. The computer stores the signals from all the detectors as a series of line images. The width of each line is small, typically 1.5 – 2 mm, corresponding to the finite width of the fan beam. Subsequently, a projection radiograph is synthesized by making a composite of these line scan images with the grey scale suitably chosen to display the anatomy with an adequate contrast – see an example image below:

The volume of tissue to be examined in CT mode can be defined once the SPR image has been generated. The CT procedure can then be automatically controlled by the computer once the appropriate scanning factors have been selected.




