XML - Managing Data Exchange/RDF - Resource Description Framework

The Resource Description Framework (RDF) is terminology used to encode, exchange and reuse metadata in the World Wide Web. Metadata, structured data about data, includes any important type of information about a resource such as author, title, creation date or language. A resource is everything that can be addressed with a Uniform Resource Identifier (URI). For example, a web page or a distinct type of document. RDF considers description as the act of making statements about the properties (attributes, characteristics) and inter-relationships of these resources. A framework is a common model to contain or manage the diverse information about a resource.

Why do we not use XML to describe things?

XML is too flexible. There are too many ways to describe things. For example, the name of a person (see code example). Each of these XML documents would map into a different logical tree. However, a query ,like what is the name of person x, has to be independent of the choice of the tree. RDF is different because it has a standard way of interpreting XML-encoded descriptions of resources which converts into one logical tree and thereby covers all possible reprensentations of a description.

<person name="Pete Maravich">

or

<person>
  <name>Pete Maravich</name>
</person>

XML documents follow a schema. The order of elements is restricted, and documents are not extensible without changing the schema. RDF allows to list information regardless of their order or appearence. RDF is also openly extensible. This means if one receives a description about something or someone, one can easily add information without being limited to following a schema. This is a great advantage, particularly for annotation and metadata applications. Besides that, it is intricate to retrieve any semantic meaning from an XML document without knowing the XML schema.

RDF is an application of XML that enforces the needed structural constraints to provide unambiguous methods of expressing semantics. XML syntax guarantees vendor independence, extensibility, validation and the ability to represent complex structures. RDF extends the general XML syntax and model to be specific for describing resources. Furthermore, RDF uses XML namespaces that allow to scope and uniquely identify a set of properties. With namespaces that point to URIs, one can generate globally unique names for its resources. Unique names need no context to qualify.

Brief History

RDF is a result of several metadata communities coming together to build a robust and flexible architecture for supporting metadata on the existing web. The first RDF specification was released 1997 by Ora Lassila and Ralph Swick. Based on that specification RDF interest groups were established in the following years and RDF became a W3C recommendation
(W3C RDF). The potential of RDF was soon realized and once its use is widespread the impacts will be tremendous. Ora Lassila said the following (W3C_NOTE_1997-11-13).

Once the web has been sufficiently "populated" with rich metadata, what can we expect? First, searching on the web will become easier as search engines have more information available, and thus searching can be more focused. Doors will also be opened for automated software agents to roam the web, looking for information for us or transacting business on our behalf. The web of today, the vast unstructured mass of information, may in the future be transformed into something more manageable - and thus something far more useful.

Purpose

Besides the human-readable display of metadata RDF is intended to enable the exchange of information between different applications without any loss of meaning. The effective use of metadata among applications, however, requires common conventions about semantics syntax, and structure. RDF imposes these conventions that make an unambiguous transfer possible. Application areas include resource description, site-maps, content rating, electronic commerce, collaborative services, and privacy preferences. Earlier one of the major obstacles of metadata interoperability has been the multiplicity of incompatible standards for metadata syntax and schema definition languages. However since RDF is a W3C recommendation and communities provide a standard vocabulary to describe things application designers and developers can create applications that allow metadata exchange in a standardized way.

The Basic Structure

Statements

With RDF one can make statements about resources. Below you can see an example of a statement that can be made about a web page. The key parts of the statement are highlighted:

http://www.example.org/index.html has an author whose name is Pete Maravich.

In general a RDF statement is a triple that contains a:

Resource, the subject of a statement
Property, the predicate of a statement
Value, the object of a statement

RDF is based on the concept that every resources can have different properties which have values. A resources, represented by an URI reference, can be fully described by using properties and their values. Other properties for this web page could be:

http://www.example.org/index.html has a language which is English.
or
http://www.example.org/index.html has a title which is Example_Title.

Graphs

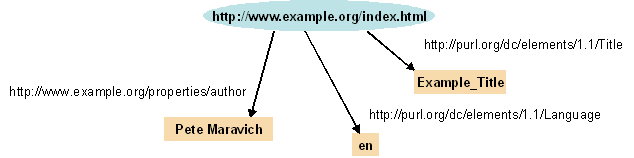
An RDF statement is a structured triple that contains a subject, a predicate and an object. A set of such triples is called a graph where a subject is always a node, a predicate is always an arc and an object is always a node:

Figure 1 - Abstract RDF graph

The set of example statements can be represented by the following graph:

Figure 2 - Example graph

Subject	http://www.example.org/index.html	is either an URI reference or a blank node
Predicate	http://purl.org/dc/elements/1.1/Title	is an URI reference
Object	Example_Title	can either be an URI reference, a literal or a blank node

RDF/XML

Natural English sentences and graphs that represent RDF's concept model are very useful pratices to understand the basics of RDF. However RDF uses a normative XML syntax called RDF/XML to put down and exchange graphs. Like HTML, RDF/XML is machine processable and, using URIs, can link pieces of information. But, unlike conventional hypertext, RDF URIs can refer to any identifiable thing, including things that may not be directly retrievable on the Web (such as persons).

The following lines represent the graph in Figure 2 in RDF/XML:

 <?xml version="1.0"?><br>
 <rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#"
          xmlns:dc="http://purl.org/dc/elements/1.1/"
          xmlns:property="http://www.example.org/properties/"> <br>
     <rdf:Description rdf:about="http://www.example.org/index.html">
         <property:author>Pete Maravich</property:author>
     </rdf:Description> <br>
     <rdf:Description rdf:about="http://www.example.org/index.html">
         <dc:language>en</dc:language>
     </rdf:Description> <br>
     <rdf:Description rdf:about="http://www.example.org/index.html">
         <dc:title>Example_Title</dc:title> 
     </rdf:Description> <br>
 </rdf:RDF>

Figure 3 - example_rdf.rdf

Let's examine the lines of code to get a better understanding of the syntax:

{1} XML declaration, identifies the document as XML in the current version 1.0
{2} Start of an rdf:RDF element, identifies the following code as RDF - also declares an XML namespace rdf, all tags starting with the prefix rdf: are part of the namespace identified by the URIref http://www.w3.org/1999/02/22-rdf-syntax-ns# which describe the RDF vocabulary
{3} declares an XML namespace dc, all tags starting with the prefix dc: are part of the namespace identified by the URIref http://purl.org/dc/elements/1.1/ - the link defines a standard vocabulary of terms for metadata
{4} declares an XML namespace property, all tags starting with the prefix property: are part of the namespace identified by the URIref http://www.example.org/properties/ - this URI is fictitious and was chosen to indicate that one can create their own vocaburaly to describe resources
{5 to 7} represents a specific statement about the resource http://www.example.org/index.html as seen in the examples - Line 5 declares the subject of the description - Line 6 provides a property element, the qualified name property is an abbreviation that represents the assigned namespace (line 4), property:author stands for http://www.example.org/properties/author - embedded in the property tag is the value(object) of the description as a plain literal

{8 to 10} shows another statement - Line 8 again provides the subject - dc:language specifies the predicate for the statement, http://purl.org/dc/elements/1.1/language - the literal 'en' is an international standard two-letter code for English

{11 to 13} shows yet another statement - Line 10 to identify the subject - dc:title specifies the predicate for the statement, http://purl.org/dc/elements/1.1/title - the value Example_Title is the object
{14} ends the rdf:RDF element

Section 3 has covererd the basic structure of RDF and is intended to provide a fundamental understanding of the topic. The next section will cover some advanced structures and features of RDF.

Advanced Concepts

Structured Property Values and Blank Nodes

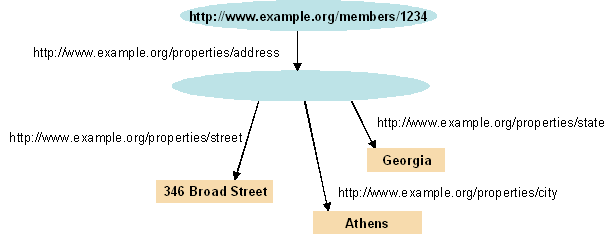
As mentioned earlier the object of a statement can be a literal, a blank node or a URI reference. The latter two give RDF more power because they allow to create complex structures, so called structured property values. For instance you consider describing the address of somebody. An address is a structure that consists of different values such as a street, a city, a state and a zipcode. In RDF one would identify the adress as a resource to allow a more detailed description.

Figure 4 - structured RDF graph

As you can see the value of the property creator is represented by a reference using the URI http://www.example.org/members/1234. RDF statements (additional arcs and nodes) can then be written with that node as the subject, to represent the additional information like the name of the creator and his address. The property adress itself is represented by a URI, which allows a detailed description that is aggregated from further statements about the address.

However the URIref http://www.example.org/address/1234 may never need to be referred to directly from outside a particular graph, and therefore may not require a specific identifier. The concept above could also be represented by using a blank node for the address object. Blank nodes were called anonymous resources, they have no URIrefs and no literals.

Figure 5 - structured RDF graph using a blank node

In RDF/XML the concept of structured property values and blank nodes are represented like this:

 <?xml version="1.0"?><br>
 <rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#"
          xmlns:dc="http://purl.org/dc/elements/1.1/"
          xmlns:property="http://www.example.org/properties/"> <br>
     <rdf:Description rdf:about="http://www.example.org/index.html">
         <dc:creator>
             <rdf:Description rdf:about="http://www.example.org/members/1234">
                 <properties:name>Pete Maravich</properties:name>
                 <properties:address rdf:nodeID="abc"/>
             </rdf:Description>
         </dc:creator>
     </rdf:Description><br>
     <rdf:Description rdf:nodeID="abc">
         <properties:street>346 Broad Street</properties:street>
         <properties:city>Athens</properties:city>
         <properties:state>Georgia</properties:state>
     </rdf:Description> <br>
 </rdf:RDF>

Figure 6 - structured_rdf.xml

Let's examine the lines of code that represent the new concepts:

{5 to 12} describes the resource http://www.example.org/index.html that has the value http://www.example.org/members/1234
{7 to 10} displays a way to abbreviate multiple property elements for a resource - usually a node has multiple arcs(properties) coming off and instead of writing one description for each property one can abbreviate this by using multiple child property elements inside the node element describing the subject node
{9} shows how one can identify a blank node in RDF/XML - it is sometimes necessary that the same blank node in a graph is referred to in the RDF/XML in multiple places - if so, a blank node identifier can be given to the blank node for identifying it in the document
{13-17} displays the properties and values for the blank node identified in line {9}

RDF applications

Dublin Core Metadata Initiative

The Dublin Core Metadata Initiative (DCMI) is an organization dedicated to promoting the widespread adoption of interoperable metadata standards and developing specialized metadata vocabularies for describing resources that enable more intelligent information discovery systems.
Basically the Dublin Core is a set of elements that are used to describe a document. The goal of the Dublin Core is to provide a minimal set of descriptive elements that support and simplify the description and the automated indexing of document-like networked objects. Discovery tools on the Internet, such as the "Webcrawlers" employed by popular World Wide Web search engines use the metadata set. In addition, the Dublin Core is meant to be sufficiently simple to be understood and used by the wide range of authors and casual publishers who contribute information to the Internet. (also see RFC-2413)

Dublin Core Metadata Element Set shows a description of all current elements defined in the Dublin Core. In the following example one can see an RDF document that uses the Dublin Core elements to describe an article in a magazine:

 <?xml version="1.0"?><br>
 <rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#"
          xmlns:dc="http://purl.org/dc/elements/1.1/"
          xmlns:dcterms="http://purl.org/dc/terms/"><br>
     <rdf:Description rdf:about="http://www.cio.com/archive/101504/km.html">
         <dc:title>Less for Success</dc:title>
         <dc:creator>Alice Dragoon</dc:creator>
         <dc:subject>
             <rdf:Bag>
                 <rdf:li>knowledge management</rdf:li>
                 <rdf:li>technology investments</rdf:li>
             </rdf:Bag>
         </dc:subject>
         <dc:description>Forget the big bang approach. When it comes to demonstrating the value
          of knowledge management, a piecemeal strategy works best.</dc:description>
         <dc:publisher>CXO Media</dc:publisher>
         <dcterms:issued>October 15, 2004</dcterms:issued>
         <dc:format>text/html</dc:format>
         <dc:language>en</dc:language>
         <dcterms:isPartOf rdf:resource="http://www.cio.com/archive/101504/index.html"/>
     </rdf:Description><br>
 </rdf:RDF>

Figure 7 - cio_article.rdf

Adobe's XMP

The Extensible Metadata Platform is a specification describing RDF-based data and storage models for metadata about documents in any format. XMP can be included in text files such as HTML or SVG, image formats such as JPEG or GIF and Adobe's own formats like Photoshop or Acrobat. Adobe is making efforts that all of their applications will support XMP. However Adobe claims that XMP provides a standard format for the creation, processing and interchange of metadata, the specification is not a standard.

XMP provides the following:

A data model - as a useful and flexible way of describing metadata in documents.
A storage model - for the implementation of the data model. This includes the serialization of the metadata as a stream of XML and XMP Packets, a means of packaging the data in files.
Schemas - predefined sets of metadata property definitions that are relevant for a wide range of applications, including all of Adobe’s editing and publishing products, as well as for applications from a wide variety of vendors. XMP also provides guidelines for the extension and addition of schemas.

However XMP metadata vocubularly is relatively small,i.e. the ways to describe a document are limited. To overcome this issue Adobe is using metadata standards such as the Dublin Core and also allows users to define their own metadata vocaburlarly.

The following screenshot is from Acrobat Professional 6.0 Document Metadata feature. The description field allows users to define metadata, whereas the advanced tab shows an overview of the metadata. Under view Source one can see the metadata in RDF/XML.

Abobe XMP example
Figure 8 - Adobe XMP example

The RDF/XML based representation of the document's metadata can be found here. The property funFactor expresses the hilariousness of a document. It was included using the 'load' functionality of Acrobat Professional to test the addition of arbitrary metadata to the properties Acrobat Professional already knew about.

RSS - RDF Site Summary

RDF Site Summary (RSS) is also an application of RDF. Please have a look at the Chapter on RSS in this Wikibook.

Creating an RDF Vocabulary

As seen earlier in the chapter one can create its own RDF metadata vocabulary, despite using standards like the Dublin Core. This section is intended to show a very general approach in creating such a personal vocabulary. For a detailed description please see Practical RDF - Powers 2003.

The first step in creating a vocabulary is to define the domain elements and their properties within the given area interest. This means one has to outline what kind of information about the resource should be described. Let's say we want to save the following facts about a resource:

Property	Description
Title	Title of the resource
Created	Date of creation
Author	Author of the resource
Status	Current status of the resource
Subject	Subject/topic of the resource
Format	Format of the resource
FunFactor	FunFactor of the resource

The next step is to create a RDF Schema(RDFS) document for the new vocabulary:

Here you can see the definition for our desired properties. Using this RDFS one can describe the article seen above the following way:

 <?xml version="1.0"?><br>
 <rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#"
          xmlns:same="http://mitglied.lycos.de/virtuoso5/elements/1.0/myschema#"><br>
     <rdf:Description rdf:about="http://www.cio.com/archive/101504/km.html">
         <same:title>Less for Success</same:title>
         <same:author>Alice Dragoon</same:author>
         <same:subject>
             <rdf:Bag>
                 <rdf:li>knowledge management</rdf:li>
                 <rdf:li>technology investments</rdf:li>
            </rdf:Bag>
         </same:subject>
         <same:format>text/html</same:format>
         <same:status>active</same:status>
         <same:created>2004-10-19</same:created>
         <same:funFactor>3</same:funFactor>
     </rdf:Description><br>
 </rdf:RDF>

Figure 9 - cio_article2.rdf

To validate its RDFS and RDF files one can use the W3C RDF Validator.

Exercises

Create an RDF/XML document that describes an article of your choice (e.g. from magazines like CIO.com or ZDNet.com). Use the Dublin Core element set and the Dublin Core termsas a framework for your description. After completing the document please validate your work with the
W3C RDF Validator.

References

RDF Primer - W3C Recommendation 10 February 2004, http://www.w3.org/TR/rdf-primer/
Shelley Powers - Practical RDF, O'Reilly 2003
Tim Berners-Lee Why RDF model is different from the XML model, September 1998, http://www.w3.org/DesignIssues/RDF-XML.html
Dublin Core Metadata Initiative - http://dublincore.org/
Adobe XMP - http://www.adobe.com/products/xmp/main.html
XML.com - XMP Lowdown, http://www.xml.com/pub/a/2004/09/22/xmp.html