User:Dirk Hünniger/gsl
Introduction
[edit | edit source]| This page is the introduction for the collection Wikibooks:Collections/GLSL Programming in Unity. It should not be referenced by other pages. |
About GLSL
[edit | edit source]GLSL (OpenGL Shading Language) is one of several commonly used shading languages for real-time rendering (other examples are Cg and HLSL). These shading languages are used to program shaders (i.e. more or less small programs) that are executed on a GPU (graphics processing unit), i.e. the processor of the graphics system of a computer – as opposed to the CPU (central processing unit) of a computer.
GPUs are massively parallel processors, which are extremely powerful. Most of today's real-time graphics in games and other interactive graphical applications would not be possible without GPUs. However, to take full advantage of the performance of GPUs, it is necessary to program them directly. This means that small programs (i.e. shaders) have to be written that can be executed by GPUs. The programming languages to write these shaders are shading languages. GLSL is one of them. In fact, it is the shading language of several 3D graphics APIs (application programming interfaces), namely OpenGL, OpenGL ES 2.x, and WebGL. Therefore, GLSL is commonly used in applications for desktop computers, mobile devices, and the web.
About this Wikibook
[edit | edit source]This wikibook was written with students in mind, who like neither programming nor mathematics. The basic motivation for this book is the observation that students are much more motivated to learn programming environments, programming languages and APIs if they are working on specific projects. Such projects are usually developed on specific platforms and therefore the approach of this book is to present GLSL within the game engine Unity.
Chapters 1 to 8 of the book consist of tutorials with working examples that produce certain effects. Note that these tutorials assume that you read them in the order in which they are presented, i.e. each tutorial will assume that you are familiar with the concepts and techniques introduced by previous tutorials. If you are new to GLSL or Unity you should at least read through the tutorials in Chapter 1, “Basics”.
More details about the OpenGL pipeline and GLSL syntax in general are included in an “Appendix on the OpenGL Pipeline and GLSL Syntax”. Readers who are not familiar with OpenGL or GLSL might want to at least skim this part since a basic understanding of the OpenGL pipeline and GLSL syntax is very useful for understanding the tutorials.
About GLSL in Unity
[edit | edit source]GLSL programming in the game engine Unity is considerably easier than GLSL programming for an OpenGL, OpenGL ES, or WebGL application. Import of meshes and images (i.e. textures) is supported by a graphical user interface; mipmaps and normal maps can be computed automatically; the most common vertex attributes and uniforms are predefined; OpenGL states can be set by very simple commands; etc.
A free version of Unity can be downloaded for Windows and MacOS at Unity's download page. All of the included tutorials work with the free version. Three points should be noted:
- First, Windows users have to use the command-line argument
-force-opengl[1] when starting Unity in order to be able to use GLSL shaders; for example, by changing theTargetsetting in the properties of the desktop icon to:"C:\Program Files\Unity\Editor\Unity.exe" -force-opengl. (On MacOS X, OpenGL and therefore GLSL is used by default.) Note that GLSL shaders cannot be used in Unity applications running in web browser on Windows. - Secondly, this book assumes that readers are somewhat familiar with Unity. If this is not the case, readers should consult the first three sections of Unity's User Guide [2] (Unity Basics, Building Scenes, Asset Import and Creation).
- Furthermore, as of version 3.5, Unity supports a version of GLSL similar to version 1.0.x for OpenGL ES 2.0 (the specification is available at the “Khronos OpenGL ES API Registry”); however, Unity's shader documentation [3] focuses on shaders written in Unity's own “surface shader” format and Cg/HLSL [4]. There are only very few details documented that are specific to GLSL shaders [5]. Thus, this wikibook might also help to close some gaps in Unity's documentation. However, optimizations (see, for example, this blog) are usually not discussed.
Martin Kraus, August 2012

Minimal Shader
[edit | edit source]This tutorial covers the basic steps to create a minimal GLSL shader in Unity.
Starting Unity and Creating a New Project
[edit | edit source]After downloading and starting Unity (Windows users have to use the command-line argument -force-opengl ), you might see an empty project. If not, you should create a new project by choosing File > New Project... from the menu. For this tutorial, you don't need to import any packages but some of the more advanced tutorials require the scripts and skyboxes packages. After creating a new project on Windows, Unity might start without OpenGL support; thus, Windows users should always quit Unity and restart it (with the command-line argument -force-opengl) after creating a new project. Then you can open the new project with File > Open Project... from the menu.
If you are not familiar with Unity's Scene View, Hierarchy View, Project View and Inspector View, now would be a good time to read the first two (or three) sections (“Unity Basics” and “Building Scenes”) of the Unity User Guide.
Creating a Shader
[edit | edit source]Creating a GLSL shader is not complicated: In the Project View, click on Create and choose Shader. A new file named “NewShader” should appear in the Project View. Double-click it to open it (or right-click and choose Open). An editor with the default shader in Cg should appear. Delete all the text and copy & paste the following shader into this file:
Shader "GLSL basic shader" { // defines the name of the shader
SubShader { // Unity chooses the subshader that fits the GPU best
Pass { // some shaders require multiple passes
GLSLPROGRAM // here begins the part in Unity's GLSL
#ifdef VERTEX // here begins the vertex shader
void main() // all vertex shaders define a main() function
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
// this line transforms the predefined attribute
// gl_Vertex of type vec4 with the predefined
// uniform gl_ModelViewProjectionMatrix of type mat4
// and stores the result in the predefined output
// variable gl_Position of type vec4.
}
#endif // here ends the definition of the vertex shader
#ifdef FRAGMENT // here begins the fragment shader
void main() // all fragment shaders define a main() function
{
gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);
// this fragment shader just sets the output color
// to opaque red (red = 1.0, green = 0.0, blue = 0.0,
// alpha = 1.0)
}
#endif // here ends the definition of the fragment shader
ENDGLSL // here ends the part in GLSL
}
}
}
Save the shader (by clicking the save icon or choosing File > Save from the editor's menu).
Congratulations, you have just created a shader in Unity. If you want, you can rename the shader file in the Project View by clicking the name, typing a new name, and pressing Return. (After renaming, reopen the shader in the editor to make sure that you are editing the correct file.)
Unfortunately, there isn't anything to see until the shader is attached to a material.
Creating a Material and Attaching a Shader
[edit | edit source]To create a material, go back to Unity and create a new material by clicking Create in the Project View and choosing Material. A new material called “New Material” should appear in the Project View. (You can rename it just like the shader.) If it isn't selected, select it by clicking. Details about the material appear now in the Inspector View. In order to set the shader to this material, you can either
- drag & drop the shader in the Project View over the material or
- select the material in the Project View and then in the Inspector View choose the shader (in this case “GLSL basic shader” as specified in the shader code above) from the drop-down list labeled Shader.
In either case, the Preview in the Inspector View of the material should now show a red sphere. If it doesn't and an error message is displayed at the bottom of the Unity window, you should reopen the shader and check in the editor whether the text is the same as given above. Windows users should make sure that OpenGL is supported by restarting Unity with the command-line argument -force-opengl.
Interactively Editing Shaders
[edit | edit source]This would be a good time to play with the shader; in particular, you can easily change the computed fragment color. Try neon green by opening the shader and replacing the fragment shader with this code:
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(0.6, 1.0, 0.0, 1.0);
// red = 0.6, green = 1.0, blue = 0.0, alpha = 1.0
}
#endif
You have to save the code in the editor and activate the Unity window again to apply the new shader. If you select the material in the Project View, the sphere in the Inspector View should now be green. You could also try to modify the red, green, and blue components to find the warmest orange or the darkest blue. (Actually, there is a movie about finding the warmest orange and another about dark blue that is almost black.)
You could also play with the vertex shader, e.g. try this vertex shader:
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix
* (vec4(1.0, 0.1, 1.0, 1.0) * gl_Vertex);
}
#endif
This flattens any input geometry by multiplying the coordinate with . (This is a component-wise vector product; for more information on vectors and matrices in GLSL see the discussion in Section “Vector and Matrix Operations”.)
In case the shader does not compile, Unity displays an error message at the bottom of the Unity window and displays the material as bright magenta. In order to see all error messages and warnings, you should select the shader in the Project View and read the messages in the Inspector View, which also include line numbers, which you can display in the text editor by choosing View > Line Numbers in the text editor menu. You could also open the Console View by choosing Window > Console from the menu, but this will not display all error messages and therefore the crucial error is often not reported.
Attaching a Material to a Game Object
[edit | edit source]We still have one important step to go: attaching the new material to a triangle mesh. To this end, create a sphere (which is one of the predefined game objects of Unity) by choosing GameObject > Create Other > Sphere from the menu. A sphere should appear in the Scene View and the label “Sphere” should appear in the Hierarchy View. (If it doesn't appear in the Scene View, click it in the Hierarchy View, move (without clicking) the mouse over the Scene View and press “f”. The sphere should now appear centered in the Scene View.)
To attach the material to the new sphere, you can:
- drag & drop the material from the Project View over the sphere in the Hierarchy View or
- drag & drop the material from the Project View over the sphere in the Scene View or
- select the sphere in the Hierarchy View, locate the Mesh Renderer component in the Inspector View (and open it by clicking the title if it isn't open), open the Materials setting of the Mesh Renderer by clicking it. Change the “Default-Diffuse” material to the new material by clicking the dotted circle icon to the right of the material name and choosing the new material from the pop-up window.
In any case, the sphere in the Scene View should now have the same color as the preview in the Inspector View of the material. Changing the shader should (after saving and switching to Unity) change the appearance of the sphere in the Scene View.
Saving Your Work in a Scene
[edit | edit source]There is one more thing: you should save you work in a “scene” (which often corresponds to a game level). Choose File > Save Scene (or File > Save Scene As...) and choose a file name in the “Assets” directory of your project. The scene file should then appear in the Project View and will be available the next time you open the project.
One More Note about Terminology
[edit | edit source]It might be good to clarify the terminology. In GLSL, a “shader” is either a vertex shader or a fragment shader. The combination of both is called a “program”.
Unfortunately, Unity refers to this kind of program as a “shader”, while in Unity a vertex shader is called a “vertex program” and a fragment shader is called a “fragment program”.
To make the confusion perfect, I'm going to use Unity's word “shader” for a GLSL program, i.e. the combination of a vertex and a fragment shader. However, I will use the GLSL terms “vertex shader” and “fragment shader” instead of “vertex program” and “fragment program”.
Summary
[edit | edit source]Congratulations, you have reached the end of this tutorial. A few of the things you have seen are:
- How to create a shader.
- How to define a GLSL vertex and fragment shader in Unity.
- How to create a material and attach a shader to the material.
- How to manipulate the ouput color
gl_FragColorin the fragment shader. - How to transform the input attribute
gl_Vertexin the vertex shader. - How to create a game object and attach a material to it.
Actually, this was quite a lot of stuff.
Further Reading
[edit | edit source]If you still want to know more
- about vertex and fragment shaders in general, you should read the description in Section “OpenGL ES 2.0 Pipeline”.
- about the vertex transformations such as
gl_ModelViewProjectionMatrix, you should read Section “Vertex Transformations”. - about handling vectors (e.g. the
vec4type) and matrices in GLSL, you should read Section “Vector and Matrix Operations”. - about how to apply vertex transformations such as
gl_ModelViewProjectionMatrix, you should read Section “Applying Matrix Transformations”. - about Unity's ShaderLab language for specifying shaders, you should read Unity's ShaderLab reference.
RGB Cube
[edit | edit source]
This tutorial introduces varying variables. It is based on Section “Minimal Shader”.
In this tutorial we will write a shader to render an RGB cube similar to the one shown to the left. The color of each point on the surface is determined by its coordinates; i.e., a point at position has the color . For example, the point is mapped to the color , i.e. pure blue. (This is the blue corner in the lower right of the figure to the left.)
Preparations
[edit | edit source]Since we want to create an RGB cube, you first have to create a cube game object. As described in Section “Minimal Shader” for a sphere, you can create a cube game object by selecting GameObject > Create Other > Cube from the main menu. Continue with creating a material and a shader object and attaching the shader to the material and the material to the cube as described in Section “Minimal Shader”.
The Shader Code
[edit | edit source]Here is the shader code, which you should copy & paste into your shader object:
Shader "GLSL shader for RGB cube" {
SubShader {
Pass {
GLSLPROGRAM
#ifdef VERTEX // here begins the vertex shader
varying vec4 position;
// this is a varying variable in the vertex shader
void main()
{
position = gl_Vertex + vec4(0.5, 0.5, 0.5, 0.0);
// Here the vertex shader writes output data
// to the varying variable. We add 0.5 to the
// x, y, and z coordinates, because the
// coordinates of the cube are between -0.5 and
// 0.5 but we need them between 0.0 and 1.0.
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif // here ends the vertex shader
#ifdef FRAGMENT // here begins the fragment shader
varying vec4 position;
// this is a varying variable in the fragment shader
void main()
{
gl_FragColor = position;
// Here the fragment shader reads intput data
// from the varying variable. The red, gree, blue,
// and alpha component of the fragment color are
// set to the values in the varying variable.
}
#endif // here ends the fragment shader
ENDGLSL
}
}
}
If your cube is not colored correctly, check the console for error messages (by selecting Window > Console from the main menu), make sure you have saved the shader code, and check whether you have attached the shader object to the material object and the material object to the game object.
Varying Variables
[edit | edit source]The main task of our shader is to set the output fragment color (gl_FragColor) in the fragment shader to the position (gl_Vertex) that is available in the vertex shader. Actually, this is not quite true: the coordinates in gl_Vertex for Unity's default cube are between -0.5 and +0.5 while we would like to have color components between 0.0 and 1.0; thus, we need to add 0.5 to the x, y, and z component, which is done by this expression: gl_Vertex + vec4(0.5, 0.5, 0.5, 0.0).
The main problem, however, is: how do we get any value from the vertex shader to the fragment shader? It turns out that the only way to do this is to use varying variables (or varyings for short). Output of the vertex shader can be written to a varying variable and then it can be read as input by the fragment shader. This is exactly what we need.
To specify a varying variable, it has to be defined with the modifier varying (before the type) in the vertex and the fragment shader outside of any function; in our example: varying vec4 position;. And here comes the most important rule about varying variables:
| The type and name of a varying variable definition in the vertex shader has to match exactly the type and name of a varying variable definition in the fragment shader and vice versa. |
This is required to avoid ambiguous cases where the GLSL compiler cannot figure out which varying variable of the vertex shader should be matched to which varying variable of the fragment shader.
A Neat Trick for Varying Variables in Unity
[edit | edit source]The requirement that the definitions of varying variables in the vertex and fragment shader match each other often results in errors, for example if a programmer changes a type or name of a varying variable in the vertex shader but forgets to change it in the fragment shader. Fortunately, there is a nice trick in Unity that avoids the problem. Consider the following shader:
Shader "GLSL shader for RGB cube" {
SubShader {
Pass {
GLSLPROGRAM // here begin the vertex and the fragment shader
varying vec4 position;
// this line is part of the vertex and the fragment shader
#ifdef VERTEX
// here begins the part that is only in the vertex shader
void main()
{
position = gl_Vertex + vec4(0.5, 0.5, 0.5, 0.0);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
// here ends the part that is only in the vertex shader
#ifdef FRAGMENT
// here begins the part that is only in the fragment shader
void main()
{
gl_FragColor = position;
}
#endif
// here ends the part that is only in the fragment shader
ENDGLSL // here end the vertex and the fragment shader
}
}
}
As the comments in this shader explain, the line #ifdef VERTEX doesn't actually mark the beginning of the vertex shader but the beginning of a part that is only in the vertex shader. Analogously, #ifdef FRAGMENT marks the beginning of a part that is only in the fragment shader. In fact, both shaders begin with the line GLSLPROGRAM. Therefore, any code between GLSLPROGRAM and the first #ifdef line will be shared by the vertex and the fragment shader. (If you are familiar with the C or C++ preprocessor, you might have guessed this already.)
This is perfect for definitions of varying variables because it means that we may type the definition only once and it will be put into the vertex and the fragment shader; thus, matching definitions are guaranteed! I.e. we have to type less and there is no way to produce compiler errors because of mismatches between the definitions of varying variables. (Of course, the cost is that we have to type all these #ifdef and #end lines.)
Variations of this Shader
[edit | edit source]The RGB cube represents the set of available colors (i.e. the gamut of the display). Thus, it can also be used show the effect of a color transformation. For example, a color to gray transformation would compute either the mean of the red, green, and blue color components, i.e. , and then put this value in all three color components of the fragment color to obtain a gray value of the same intensity. Instead of the mean, the relative luminance could also be used, which is . Of course, any other color transformation (changing saturation, contrast, hue, etc.) is also applicable.
Another variation of this shader could compute a CMY (cyan, magenta, yellow) cube: for position you could subtract from a pure white an amount of red that is proportional to in order to produce cyan. Furthermore, you would subtract an amount of green in proportion to the component to produce magenta and also an amount of blue in proportion to to produce yellow.
If you really want to get fancy, you could compute an HSV (hue, saturation, value) cylinder. For and coordinates between -0.5 and +0.5, you can get an angle between 0 and 360° with 180.0+degrees(atan(z, x)) in GLSL and a distance between 0 and 1 from the axis with 2.0 * sqrt(x * x + z * z). The coordinate for Unity's built-in cylinder is between -1 and 1 which can be translated to a value between 0 and 1 by . The computation of RGB colors from HSV coordinates is described in the article on HSV in Wikipedia.
Interpolation of Varying Variables
[edit | edit source]The story about varying variables is not quite over yet. If you select the cube game object, you will see in the Scene View that it consists of only 12 triangles and 8 vertices. Thus, the vertex shader might be called only eight times and only eight different outputs are written to the varying variable. However, there are many more colors on the cube. How did that happen?
The answer is implied by the name varying variables. They are called this way because they vary across a triangle. In fact, the vertex shader is only called for each vertex of each triangle. If the vertex shader writes different values to a varying variable for different vertices, the values are interpolated across the triangle. The fragment shader is then called for each pixel that is covered by the triangle and receives interpolated values of the varying variables. The details of this interpolation are described in Section “Rasterization”.
If you want to make sure that a fragment shader receives one exact, non-interpolated value by a vertex shader, you have to make sure that the vertex shader writes the same value to the varying variable for all vertices of a triangle.
Summary
[edit | edit source]And this is the end of this tutorial. Congratulations! Among other things, you have seen:
- What an RGB cube is.
- What varying variables are good for and how to define them.
- How to make sure that a varying variable has the same name and type in the vertex shader and the fragment shader.
- How the values written to a varying variable by the vertex shader are interpolated across a triangle before they are received by the fragment shader.
Further Reading
[edit | edit source]If you want to know more
- about the data flow in and out of vertex and fragment shaders, you should read the description in Section “OpenGL ES 2.0 Pipeline”.
- about vector and matrix operations (e.g. the expression
gl_Vertex + vec4(0.5, 0.5, 0.5, 0.0);), you should read Section “Vector and Matrix Operations”. - about the interpolation of varying variables, you should read Section “Rasterization”.
- about Unity's official documentation of writing vertex shaders and fragment shaders in Unity's ShaderLab, you should read Unity's ShaderLab reference about “GLSL Shader Programs”.
Debugging of Shaders
[edit | edit source]
This tutorial introduces attribute variables. It is based on Section “Minimal Shader” and Section “RGB Cube”.
This tutorial also introduces the main technique to debug shaders in Unity: false-color images, i.e. a value is visualized by setting one of the components of the fragment color to it. Then the intensity of that color component in the resulting image allows you to make conclusions about the value in the shader. This might appear to be a very primitive debugging technique because it is a very primitive debugging technique. Unfortunately, there is no alternative in Unity.
Where Does the Vertex Data Come from?
[edit | edit source]In Section “RGB Cube” you have seen how the fragment shader gets its data from the vertex shader by means of varying variables. The question here is: where does the vertex shader get its data from? Within Unity, the answer is that the Mesh Renderer component of a game object sends all the data of the mesh of the game object to OpenGL in each frame. (This is often called a “draw call”. Note that each draw call has some performance overhead; thus, it is much more efficient to send one large mesh with one draw call to OpenGL than to send several smaller meshes with multiple draw calls.) This data usually consists of a long list of triangles, where each triangle is defined by three vertices and each vertex has certain attributes, including position. These attributes are made available in the vertex shader by means of attribute variables.
Built-in Attribute Variables and how to Visualize Them
[edit | edit source]In Unity, most of the standard attributes (position, color, surface normal, and texture coordinates) are built in, i.e. you need not (in fact must not) define them. The names of these built-in attributes are actually defined by the OpenGL “compability profile” because such built-in names are needed if you mix an OpenGL application that was written for the fixed-function pipeline with a (programmable) vertex shader. If you had to define them, the definitions (only in the vertex shader) would look like this:
attribute vec4 gl_Vertex; // position (in object coordinates,
// i.e. local or model coordinates)
attribute vec4 gl_Color; // color (usually constant)
attribute vec3 gl_Normal; // surface normal vector
// (in object coordinates; usually normalized to unit length)
attribute vec4 gl_MultiTexCoord0; //0th set of texture coordinates
// (a.k.a. “UV”; between 0 and 1)
attribute vec4 gl_MultiTexCoord1; //1st set of texture coordinates
// (a.k.a. “UV”; between 0 and 1)
...
There is only one attribute variable that is provided by Unity but has no standard name in OpenGL, namely the tangent vector, i.e. a vector that is orthogonal to the surface normal. You should define this variable yourself as an attribute variable of type vec4 with the specific name Tangent as shown in the following shader:
Shader "GLSL shader with all built-in attributes" {
SubShader {
Pass {
GLSLPROGRAM
#ifdef VERTEX
varying vec4 color;
attribute vec4 Tangent; // this attribute is specific to Unity
void main()
{
color = gl_MultiTexCoord0; // set the varying variable
// other possibilities to play with:
// color = gl_Vertex;
// color = gl_Color;
// color = vec4(gl_Normal, 1.0);
// color = gl_MultiTexCoord0;
// color = gl_MultiTexCoord1;
// color = Tangent;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
varying vec4 color;
void main()
{
gl_FragColor = color; // set the output fragment color
}
#endif
ENDGLSL
}
}
}
In Section “RGB Cube” we have already seen, how to visualize the gl_Vertex coordinates by setting the fragment color to those values. In this example, the fragment color is set to gl_MultiTexCoord0 such that we can see what kind of texture coordinates Unity provides.
Note that only the first three components of Tangent represent the tangent direction. The scaling and the fourth component are set in a specific way, which is mainly useful for parallax mapping (see Section “Projection of Bumpy Surfaces”).
How to Interpret False-Color Images
[edit | edit source]When trying to understand the information in a false-color image, it is important to focus on one color component only. For example, if the standard attribute gl_MultiTexCoord0 for a sphere is written to the fragment color then the red component of the fragment visualizes the x coordinate of gl_MultiTexCoord0, i.e. it doesn't matter whether the output color is maximum pure red or maximum yellow or maximum magenta, in all cases the red component is 1. On the other hand, it also doesn't matter for the red component whether the color is blue or green or cyan of any intensity because the red component is 0 in all cases. If you have never learned to focus solely on one color component, this is probably quite challenging; therefore, you might consider to look only at one color component at a time. For example by using this line to set the varying in the vertex shader:
color = vec4(gl_MultiTexCoord0.x, 0.0, 0.0, 1.0);
This sets the red component of the varying variable to the x component of gl_MultiTexCoord0 but sets the green and blue components to 0 (and the alpha or opacity component to 1 but that doesn't matter in this shader).
If you focus on the red component or visualize only the red component you should see that it increases from 0 to 1 as you go around the sphere and after 360° drops to 0 again. It actually behaves similar to a longitude coordinate on the surface of a planet. (In terms of spherical coordinates, it corresponds to the azimuth.)
If the x component of gl_MultiTexCoord0 corresponds to the longitude, one would expect that the y component would correspond to the latitude (or the inclination in spherical coordinates). However, note that texture coordinates are always between 0 and 1; therefore, the value is 0 at the bottom (south pole) and 1 at the top (north pole). You can visualize the y component as green on its own with:
color = vec4(0.0, gl_MultiTexCoord0.y, 0.0, 1.0);
Texture coordinates are particularly nice to visualize because they are between 0 and 1 just like color components are. Almost as nice are coordinates of normalized vectors (i.e., vectors of length 1; for example, gl_Normal is usually normalized) because they are always between -1 and +1. To map this range to the range from 0 to 1, you add 1 to each component and divide all components by 2, e.g.:
color = vec4((gl_Normal + vec3(1.0, 1.0, 1.0)) / 2.0, 1.0);
Note that gl_Normal is a three-dimensional vector. Black corresponds then to the coordinate -1 and full intensity of one component to the coordinate +1.
If the value that you want to visualize is in another range than 0 to 1 or -1 to +1, you have to map it to the range from 0 to 1, which is the range of color components. If you don't know which values to expect, you just have to experiment. What helps here is that if you specify color components outside of the range 0 to 1, they are automatically clamped to this range. I.e., values less than 0 are set to 0 and values greater than 1 are set to 1. Thus, when the color component is 0 or 1 you know at least that the value is less or greater than what you assumed and then you can adapt the mapping iteratively until the color component is between 0 and 1.
Debugging Practice
[edit | edit source]In order to practice the debugging of shaders, this section includes some lines that produce black colors when the assignment to color in the vertex shader is replaced by each of them. Your task is to figure out for each line, why the result is black. To this end, you should try to visualize any value that you are not absolutely sure about and map the values less than 0 or greater than 1 to other ranges such that the values are visible and you have at least an idea in which range they are. Note that most of the functions and operators are documented in Section “Vector and Matrix Operations”.
color = gl_MultiTexCoord0 - vec4(1.5, 2.3, 1.1, 0.0);
color = vec4(gl_MultiTexCoord0.z);
color = gl_MultiTexCoord0 / tan(0.0);
The following lines require some knowledge about the dot and cross product:
color = dot(gl_Normal, vec3(Tangent)) * gl_MultiTexCoord0;
color = dot(cross(gl_Normal, vec3(Tangent)), gl_Normal) *
gl_MultiTexCoord0;
color = vec4(cross(gl_Normal, gl_Normal), 1.0);
color = vec4(cross(gl_Normal, vec3(gl_Vertex)), 1.0);
// only for a sphere!
Do the functions radians() and noise() always return black? What's that good for?
color = radians(gl_MultiTexCoord0);
color = noise4(gl_MultiTexCoord0);
Consult the documentation in the “OpenGL ES Shading Language 1.0.17 Specification” available at the “Khronos OpenGL ES API Registry” to figure out what radians() is good for and what the problem with noise4() is.
Special Variables in the Fragment Shader
[edit | edit source]Attributes are specific to vertices, i.e., they usually have different values for different vertices. There are similar variables for fragment shaders, i.e., variables that have different values for each fragment. However, they are different from attributes because they are not specified by a mesh (i.e. a list of triangles). They are also different from varyings because they are not set explicitly by the vertex shader.
Specifically, a four-dimensional vector gl_FragCoord is available containing the screen (or: window) coordinates of the fragment that is processed; see Section “Vertex Transformations” for the description of the screen coordinate system.
Moreover, a boolean variable gl_FrontFacing is provided that specifies whether the front face or the back face of a triangle is being rendered. Front faces usually face the “outside” of a model and back faces face the “inside” of a model; however, there is no clear outside or inside if the model is not a closed surface. Usually, the surface normal vectors point in the direction of the front face, but this is not required. In fact, front faces and back faces are specified by the order of the vertex triangles: if the vertices appear in counter-clockwise order, the front face is visible; if they appear in clockwise order, the back face is visible. An application is shown in Section “Cutaways”.
Summary
[edit | edit source]Congratulations, you have reached the end of this tutorial! We have seen:
- The list of built-in attributes in Unity:
gl_Vertex,gl_Color,gl_Normal,gl_MultiTexCoord0,gl_MultiTexCoord1, and the specialTangent. - How to visualize these attributes (or any other value) by setting components of the output fragment color.
- The two additional special variables that are available in fragment programs:
gl_FragCoordandgl_FrontFacing.
Further Reading
[edit | edit source]If you still want to know more
- about the data flow in vertex and fragment shaders, you should read the description in Section “OpenGL ES 2.0 Pipeline”.
- about operations and functions for vectors, you should read Section “Vector and Matrix Operations”.
Shading in World Space
[edit | edit source]
This tutorial introduces uniform variables. It is based on Section “Minimal Shader”, Section “RGB Cube”, and Section “Debugging of Shaders”.
In this tutorial we will look at a shader that changes the fragment color depending on its position in the world. The concept is not too complicated; however, there are extremely important applications, e.g. shading with lights and environment maps. We will also have a look at shaders in the real world; i.e., what is necessary to enable non-programmers to use your shaders?
Transforming from Object to World Space
[edit | edit source]As mentioned in Section “Debugging of Shaders”, the attribute gl_Vertex specifies object coordinates, i.e. coordinates in the local object (or model) space of a mesh. The object space (or object coordinate system) is specific to each game object; however, all game objects are transformed into one common coordinate system — the world space.
If a game object is put directly into the world space, the object-to-world transformation is specified by the Transform component of the game object. To see it, select the object in the Scene View or the Hierarchy View and then find the Transform component in the Inspector View. There are parameters for “Position”, “Rotation” and “Scale” in the Transform component, which specify how vertices are transformed from object coordinates to world coordinates. (If a game object is part of a group of objects, which is shown in the Hierarchy View by means of indentation, then the Transform component only specifies the transformation from object coordinates of a game object to the object coordinates of the parent. In this case, the actual object-to-world transformation is given by the combination of the transformation of a object with the transformations of its parent, grandparent, etc.) The transformations of vertices by translations, rotations and scalings, as well as the combination of transformations and their representation as 4×4 matrices are discussed in Section “Vertex Transformations”.
Back to our example: the transformation from object space to world space is put into a 4×4 matrix, which is also known as “model matrix” (since this transformation is also known as “model transformation”). This matrix is available in the uniform variable unity_ObjectToWorld(in Unity 5, maybe _Object2World in elder version), which is defined and used in the following shader:
Shader "GLSL shading in world space" {
SubShader {
Pass {
GLSLPROGRAM
uniform mat4 unity_ObjectToWorld;
// definition of a Unity-specific uniform variable
#ifdef VERTEX
varying vec4 position_in_world_space;
void main()
{
position_in_world_space = unity_ObjectToWorld * gl_Vertex;
// transformation of gl_Vertex from object coordinates
// to world coordinates;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
varying vec4 position_in_world_space;
void main()
{
float dist = distance(position_in_world_space,
vec4(0.0, 0.0, 0.0, 1.0));
// computes the distance between the fragment position
// and the origin (the 4th coordinate should always be
// 1 for points).
if (dist < 5.0)
{
gl_FragColor = vec4(0.0, 1.0, 0.0, 1.0);
// color near origin
}
else
{
gl_FragColor = vec4(0.3, 0.3, 0.3, 1.0);
// color far from origin
}
}
#endif
ENDGLSL
}
}
}
Note that this shader makes sure that the definition of the uniform is included in both the vertex and the fragment shader (although this particular fragment shader doesn't need it). This is similar to the definition of varyings discussed in Section “RGB Cube”.
Usually, an OpenGL application has to set the value of uniform variables; however, Unity takes care of always setting the correct value of predefined uniform variables such as unity_ObjectToWorld; thus, we don't have to worry about it.
This shader transforms the vertex position to world space and gives it to the fragment shader in a varying. For the fragment shader the varying variable contains the interpolated position of the fragment in world coordinates. Based on the distance of this position to the origin of the world coordinate system, one of two colors is set. Thus, if you move an object with this shader around in the editor it will turn green near the origin of the world coordinate system. Farther away from the origin it will turn dark grey.
More Unity-Specific Uniforms
[edit | edit source]There are, in fact, several predefined uniform variables similar to unity_ObjectToWorld. Here is a short list (including unity_ObjectToWorld), which appears in the shader codes of several tutorials:
// The following built-in uniforms (except _LightColor0 and
// _LightMatrix0) are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec4 _Time, _SinTime, _CosTime; // time values from Unity
uniform vec4 _ProjectionParams;
// x = 1 or -1 (-1 if projection is flipped)
// y = near plane; z = far plane; w = 1/far plane
uniform vec4 _ScreenParams;
// x = width; y = height; z = 1 + 1/width; w = 1 + 1/height
uniform vec4 unity_Scale; // w = 1/scale; see _World2Object
uniform vec3 _WorldSpaceCameraPos;
uniform mat4 unity_ObjectToWorld; // model matrix
uniform mat4 unity_WorldToObject; // inverse model matrix
// (all but the bottom-right element have to be scaled
// with unity_Scale.w if scaling is important)
uniform vec4 _LightPositionRange; // xyz = pos, w = 1/range
uniform vec4 _WorldSpaceLightPos0;
// position or direction of light source
uniform vec4 _LightColor0; // color of light source
uniform mat4 _LightMatrix0; // matrix to light space
As the comments suggest, instead of defining all these uniforms (except _LightColor0 and _LightMatrix0), you could also include the file UnityCG.glslinc. However, for some unknown reason _LightColor0 and _LightMatrix0 are not included in this file; thus, we have to define them separately:
#include "UnityCG.glslinc"
uniform vec4 _LightColor0;
uniform mat4 _LightMatrix0;
Unity does not always update all of these uniforms. In particular, _WorldSpaceLightPos0, _LightColor0, and _LightMatrix0 are only set correctly for shader passes that are tagged appropriately, e.g. with Tags {"LightMode" = "ForwardBase"} as the first line in the Pass {...} block; see also Section “Diffuse Reflection”.
More OpenGL-Specific Uniforms
[edit | edit source]Another class of built-in uniforms are defined for the OpenGL compability profile, for example the mat4 matrix gl_ModelViewProjectionMatrix, which is equivalent to the matrix product gl_ProjectionMatrix * gl_ModelViewMatrix of two other built-in uniforms. The corresponding transformations are described in detail in Section “Vertex Transformations”.
As you can see in the shader above, these uniforms don't have to be defined; they are always available in GLSL shaders in Unity. If you had to define them, the definitions would look like this:
uniform mat4 gl_ModelViewMatrix;
uniform mat4 gl_ProjectionMatrix;
uniform mat4 gl_ModelViewProjectionMatrix;
uniform mat4 gl_TextureMatrix[gl_MaxTextureCoords];
uniform mat3 gl_NormalMatrix;
// transpose of the inverse of gl_ModelViewMatrix
uniform mat4 gl_ModelViewMatrixInverse;
uniform mat4 gl_ProjectionMatrixInverse;
uniform mat4 gl_ModelViewProjectionMatrixInverse;
uniform mat4 gl_TextureMatrixInverse[gl_MaxTextureCoords];
uniform mat4 gl_ModelViewMatrixTranspose;
uniform mat4 gl_ProjectionMatrixTranspose;
uniform mat4 gl_ModelViewProjectionMatrixTranspose;
uniform mat4 gl_TextureMatrixTranspose[gl_MaxTextureCoords];
uniform mat4 gl_ModelViewMatrixInverseTranspose;
uniform mat4 gl_ProjectionMatrixInverseTranspose;
uniform mat4 gl_ModelViewProjectionMatrixInverseTranspose;
uniform mat4 gl_TextureMatrixInverseTranspose[gl_MaxTextureCoords];
struct gl_LightModelParameters { vec4 ambient; };
uniform gl_LightModelParameters gl_LightModel;
...
In fact, the compability profile of OpenGL defines even more uniforms; see Chapter 7 of the “OpenGL Shading Language 4.10.6 Specification” available at Khronos' OpenGL page. Unity supports many of them but not all.
Some of these uniforms are arrays, e.g gl_TextureMatrix. In fact, an array of matrices
gl_TextureMatrix[0], gl_TextureMatrix[1], ..., gl_TextureMatrix[gl_MaxTextureCoords - 1] is available, where gl_MaxTextureCoords is a built-in integer.
Computing the View Matrix
[edit | edit source]Traditionally, it is customary to do many computations in view space, which is just a rotated and translated version of world space (see Section “Vertex Transformations” for the details). Therefore, OpenGL offers only the product of the model matrix and the view matrix , i.e. the model-view matrix , which is available in the uniform gl_ModelViewMatrix. The view matrix is not available. Unity also doesn't provide it.
However, unity_ObjectToWorld is just the model matrix and unity_WorldToObject is the inverse model matrix. (Except that all but the bottom-right element have to be scaled by untiy_Scale.w.) Thus, we can easily compute the view matrix. The mathematics looks like this:
In other words, the view matrix is the product of the model-view matrix and the inverse model matrix (which is unity_WorldToObject * unity_Scale.w except for the bottom-right element, which is 1). Assuming that we have defined the uniforms unity_WorldToObject and unity_Scale, we can compute the view matrix this way in GLSL:
mat4 modelMatrixInverse = _World2Object * unity_Scale.w;
modelMatrixInverse[3][3] = 1.0;
mat4 viewMatrix = gl_ModelViewMatrix * modelMatrixInverse;
User-Specified Uniforms: Shader Properties
[edit | edit source]There is one more important type of uniform variables: uniforms that can be set by the user. Actually, these are called shader properties in Unity. You can think of them as parameters of the shader. A shader without parameters is usually used only by its programmer because even the smallest necessary change requires some programming. On the other hand, a shader using parameters with descriptive names can be used by other people, even non-programmers, e.g. CG artists. Imagine you are in a game development team and a CG artist asks you to adapt your shader for each of 100 design iterations. It should be obvious that a few parameters, which even a CG artist can play with, might save you a lot of time. Also, imagine you want to sell your shader: parameters will often dramatically increase the value of your shader.
Since the description of shader properties in Unity's ShaderLab reference is quite OK, here is only an example, how to use shader properties in our example. We first declare the properties and then define uniforms of the same names and corresponding types.
Shader "GLSL shading in world space" {
Properties {
_Point ("a point in world space", Vector) = (0., 0., 0., 1.0)
_DistanceNear ("threshold distance", Float) = 5.0
_ColorNear ("color near to point", Color) = (0.0, 1.0, 0.0, 1.0)
_ColorFar ("color far from point", Color) = (0.3, 0.3, 0.3, 1.0)
}
SubShader {
Pass {
GLSLPROGRAM
// uniforms corresponding to properties
uniform vec4 _Point;
uniform float _DistanceNear;
uniform vec4 _ColorNear;
uniform vec4 _ColorFar;
#include "UnityCG.glslinc"
// defines _Object2World and _World2Object
varying vec4 position_in_world_space;
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
position_in_world_space = modelMatrix * gl_Vertex;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
float dist= distance(position_in_world_space, _Point);
if (dist < _DistanceNear)
{
gl_FragColor = _ColorNear;
}
else
{
gl_FragColor = _ColorFar;
}
}
#endif
ENDGLSL
}
}
}
With these parameters, a non-programmer can modify the effect of our shader. This is nice; however, the properties of the shader (and in fact uniforms in general) can also be set by scripts! For example, a JavaScript attached to the game object that is using the shader can set the properties with these lines:
renderer.sharedMaterial.SetVector("_Point",
Vector4(1.0, 0.0, 0.0, 1.0));
renderer.sharedMaterial.SetFloat("_DistanceNear",
10.0);
renderer.sharedMaterial.SetColor("_ColorNear",
Color(1.0, 0.0, 0.0));
renderer.sharedMaterial.SetColor("_ColorFar",
Color(1.0, 1.0, 1.0));
Use sharedMaterial if you want to change the parameters for all objects that use this material and just material if you want to change the parameters only for one object. With scripting you could, for example, set the _Point to the position of another object (i.e. the position of its Transform component). In this way, you can specify a point just by moving another object around in the editor. In order to write such a script, select Create > JavaScript in the Project View and copy & paste this code:
@script ExecuteInEditMode() // make sure to run in edit mode
var other : GameObject; // another user-specified object
function Update () // this function is called for every frame
{
if (null != other) // has the user specified an object?
{
renderer.sharedMaterial.SetVector("_Point",
other.transform.position); // set the shader property
// _Point to the position of the other object
}
}
Then, you should attach the script to the object with the shader and drag & drop another object to the other variable of the script in the Inspector View.
Summary
[edit | edit source]Congratulations, you made it! (In case you wonder: yes, I'm also talking to myself here. ;) We discussed:
- How to transform a vertex into world coordinates.
- The most important Unity-specific uniforms that are supported by Unity.
- The most important OpenGL-specific uniforms that are supported by Unity.
- How to make a shader more useful and valuable by adding shader properties.
Further Reading
[edit | edit source]If you want to know more
- about vector and matrix operations (e.g. the
distance()function), you should read Section “Vector and Matrix Operations”. - about the standard vertex transformations, e.g. the model matrix and the view matrix, you should read Section “Vertex Transformations”.
- about the application of transformation matrices to points and directions, you should read Section “Applying Matrix Transformations”.
- about the specification of shader properties, you should read Unity's documentation about “ShaderLab syntax: Properties”.
Cutaways
[edit | edit source]
This tutorial covers discarding fragments, determining whether the front face or back face is rendered, and front-face and back-face culling. This tutorial assumes that you are familiar with varying variables as discussed in Section “RGB Cube”.
The main theme of this tutorial is to cut away triangles or fragments even though they are part of a mesh that is being rendered. The main two reasons are: we want to look through a triangle or fragment (as in the case of the roof in the drawing to the left, which is only partly cut away) or we know that a triangle isn't visible anyways; thus, we can save some performance by not processing it. OpenGL supports these situations in several ways; we will discuss two of them.
Very Cheap Cutaways
[edit | edit source]The following shader is a very cheap way of cutting away parts of a mesh: all fragments are cut away that have a positive coordinate in object coordinates (i.e. in the coordinate system in which it was modeled; see Section “Vertex Transformations” for details about coordinate systems). Here is the code:
Shader "GLSL shader using discard" {
SubShader {
Pass {
Cull Off // turn off triangle culling, alternatives are:
// Cull Back (or nothing): cull only back faces
// Cull Front : cull only front faces
GLSLPROGRAM
varying vec4 position_in_object_coordinates;
#ifdef VERTEX
void main()
{
position_in_object_coordinates= gl_Vertex;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
if (position_in_object_coordinates.y > 0.0)
{
discard; // drop the fragment if y coordinate > 0
}
if (gl_FrontFacing) // are we looking at a front face?
{
gl_FragColor = vec4(0.0, 1.0, 0.0, 1.0); // yes: green
}
else
{
gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0); // no: red
}
}
#endif
ENDGLSL
}
}
}
When you apply this shader to any of the default objects, the shader will cut away half of them. This is a very cheap way of producing hemispheres or open cylinders.
Discarding Fragments
[edit | edit source]Let's first focus on the discard instruction in the fragment shader. This instruction basically just discards the processed fragment. (This was called a fragment “kill” in earlier shading languages; I can understand that the fragments prefer the term “discard”.) Depending on the hardware, this can be a quite expensive technique in the sense that rendering might perform considerably worse as soon as there is one shader that includes a discard instruction (regardless of how many fragments are actually discarded, just the presence of the instruction may result in the deactivation of some important optimizations). Therefore, you should avoid this instruction whenever possible but in particular when you run into performance problems.
One more note: the condition for the fragment discard includes only an object coordinate. The consequence is that you can rotate and move the object in any way and the cutaway part will always rotate and move with the object. You might want to check what cutting in world space looks like: change the vertex and fragment shader such that the world coordinate is used in the condition for the fragment discard. Tip: see Section “Shading in World Space” for how to transform the vertex into world space.
Better Cutaways
[edit | edit source]If you are not(!) familiar with scripting in Unity, you might try the following idea to improve the shader: change it such that fragments are discarded if the coordinate is greater than some threshold variable. Then introduce a shader property to allow the user to control this threshold. Tip: see Section “Shading in World Space” for a discussion of shader properties.
If you are familiar with scripting in Unity, you could try this idea: write a script for an object that takes a reference to another sphere object and assigns (using renderer.sharedMaterial.SetMatrix()) the inverse model matrix (renderer.worldToLocalMatrix) of that sphere object to a mat4 uniform variable of the shader. In the shader, compute the position of the fragment in world coordinates and apply the inverse model matrix of the other sphere object to the fragment position. Now you have the position of the fragment in the local coordinate system of the other sphere object; here, it is easy to test whether the fragment is inside the sphere or not because in this coordinate system all spheres are centered around the origin with radius 0.5. Discard the fragment if it is inside the other sphere object. The resulting script and shader can cut away points from the surface of any object with the help of a cutting sphere that can be manipulated interactively in the editor like any other sphere.
Distinguishing between Front and Back Faces
[edit | edit source]A special boolean variable gl_FrontFacing is available in the fragment shader that specifies whether we are looking at the front face of a triangle. Usually, the front faces are facing the outside of a mesh and the back faces the inside. (Just as the surface normal vector usually points to the outside.) However, the actual way front and back faces are distinguished is the order of the vertices in a triangle: if the camera sees the vertices of a triangle in counter-clockwise order, it sees the front face. If it sees the vertices in clockwise order, it sees the back face.
Our fragment shader checks the variable gl_FrontFacing and assigns green to the output fragment color if gl_FrontFacing is true (i.e. the fragment is part of a front-facing triangle; i.e. it is facing the outside), and red if gl_FrontFacing is false (i.e. the fragment is part of a back-facing triangle; i.e. it is facing the inside). In fact, gl_FrontFacing allows you not only to render the two faces of a surfaces with different colors but with completely different styles.
Note that basing the definition of front and back faces on the order of vertices in a triangle can cause problems when vertices are mirrored, i.e. scaled with a negative factor. Unity tries to take care of these problems; thus, just specifying a negative scaling in the Transform component of the game object will usually not cause this problem. However, since Unity has no control over what we are doing in the vertex shader, we can still turn the inside out by multiplying one (or three) of the coordinates with -1, e.g. by assigning gl_Position this way in the vertex shader:
gl_Position = gl_ModelViewProjectionMatrix
* vec4(-gl_Vertex.x, gl_Vertex.y, gl_Vertex.z, 1.0);
This just multiplies the coordinate by -1. For a sphere, you might think that nothing happens, but it actually turns front faces into back faces and vice versa; thus, now the inside is green and the outside is red. (By the way, this problem also affects the surface normal vector.) Thus, be careful with mirrors!
Culling of Front or Back Faces
[edit | edit source]Finally, the shader (more specifically the shader pass) includes the line Cull Off. This line has to come before GLSLPROGRAM because it is not in GLSL. In fact, it is the command of Unity's ShaderLab to turn off any triangle culling. This is necessary because by default back faces are culled away as if the line Cull Back was specified. You can also specify the culling of front faces with Cull Front. The reason why culling of back-facing triangles is active by default, is that the inside of objects is usually invisible; thus, back-face culling can save quite some performance by avoiding to rasterize these triangles as explained next. Of course, we were able to see the inside with our shader because we have discarded some fragments; thus, we had to deactivate back-face culling.
How does culling work? Triangles and vertices are processed as usual. However, after the viewport transformation of the vertices to screen coordinates (see Section “Vertex Transformations”) the graphics processor determines whether the vertices of a triangle appear in counter-clockwise order or in clockwise order on the screen. Based on this test, each triangle is considered a front-facing or a back-facing triangle. If it is front-facing and culling is activated for front-facing triangles, it will be discarded, i.e., the processing of it stops and it is not rasterized. Analogously, if it is back-facing and culling is activated for back-facing triangles. Otherwise, the triangle will be processed as usual.
Summary
[edit | edit source]Congratulations, you have worked through another tutorial. (If you have tried one of the assignments: good job! I didn't yet.) We have looked at:
- How to discard fragments.
- How to render front-facing and back-facing triangles in different colors.
- How to deactivate the default culling of back faces.
- How to activate the culling of front faces.
Further Reading
[edit | edit source]If you still want to know more
- about the vertex transformations such as the model transformation from object to world coordinates or the viewport transformation to screen coordinates, you should read Section “Vertex Transformations”.
- about how to define shader properties, you should read Section “Shading in World Space”.
- about Unity's ShaderLab syntax for specifying culling, you should read Culling & Depth Testing.
Transparency
[edit | edit source]
This tutorial covers blending of fragments (i.e. compositing them) using GLSL shaders in Unity. It assumes that you are familiar with the concept of front and back faces as discussed in Section “Cutaways”.
More specifically, this tutorial is about rendering transparent objects, e.g. transparent glass, plastic, fabrics, etc. (More strictly speaking, these are actually semitransparent objects because they don't need to be perfectly transparent.) Transparent objects allow us to see through them; thus, their color “blends” with the color of whatever is behind them.
Blending
[edit | edit source]As mentioned in Section “OpenGL ES 2.0 Pipeline”, the fragment shader computes an RGBA color (i.e. red, green, blue, and alpha components in gl_FragColor) for each fragment (unless the fragment is discarded). The fragments are then processed as discussed in Section “Per-Fragment Operations”. One of the operations is the blending stage, which combines the color of the fragment (as specified in gl_FragColor), which is called the “source color”, with the color of the corresponding pixel that is already in the framebuffer, which is called the “destination color” (because the “destination” of the resulting blended color is the framebuffer).
Blending is a fixed-function stage, i.e. you can configure it but not program it. The way it is configured, is by specifying a blend equation. You can think of the blend equation as this definition of the resulting RGBA color:
vec4 result = SrcFactor * gl_FragColor + DstFactor * pixel_color;
where pixel_color is the RGBA color that is currently in the framebuffer and result is the blended result, i.e. the output of the blending stage. SrcFactor and DstFactor are configurable RGBA colors (of type vec4) that are multiplied component-wise with the fragment color and the pixel color. The values of SrcFactor and DstFactor are specified in Unity's ShaderLab syntax with this line:
Blend {code for SrcFactor} {code for DstFactor}
The most common codes for the two factors are summarized in the following table (more codes are mentioned in Unity's ShaderLab reference about blending):
| Code | Resulting Factor (SrcFactor or DstFactor)
|
|---|---|
One |
vec4(1.0)
|
Zero |
vec4(0.0)
|
SrcColor |
gl_FragColor
|
SrcAlpha |
vec4(gl_FragColor.a)
|
DstColor |
pixel_color
|
DstAlpha |
vec4(pixel_color.a)
|
OneMinusSrcColor |
vec4(1.0) - gl_FragColor
|
OneMinusSrcAlpha |
vec4(1.0 - gl_FragColor.a)
|
OneMinusDstColor |
vec4(1.0) - pixel_color
|
OneMinusDstAlpha |
vec4(1.0 - pixel_color.a)
|
As discussed in Section “Vector and Matrix Operations”, vec4(1.0) is just a short way of writing vec4(1.0, 1.0, 1.0, 1.0). Also note that all components of all colors and factors in the blend equation are clamped between 0 and 1.
Alpha Blending
[edit | edit source]One specific example for a blend equation is called “alpha blending”. In Unity, it is specified this way:
Blend SrcAlpha OneMinusSrcAlpha
which corresponds to:
vec4 result = vec4(gl_FragColor.a) * gl_FragColor + vec4(1.0 - gl_FragColor.a) * pixel_color;
This uses the alpha component of gl_FragColor as an opacity. I.e. the more opaque the fragment color is, the larger its opacity and therefore its alpha component, and thus the more of the fragment color is mixed in the result and the less of the pixel color in the framebuffer. A perfectly opaque fragment color (i.e. with an alpha component of 1) will completely replace the pixel color.
This blend equation is sometimes referred to as an “over” operation, i.e. “gl_FragColor over pixel_color”, since it corresponds to putting a layer of the fragment color with a specific opacity on top of the pixel color. (Think of a layer of colored glass or colored semitransparent plastic on top of something of another color.)
Due to the popularity of alpha blending, the alpha component of a color is often called opacity even if alpha blending is not employed. Moreover, note that in computer graphics a common formal definition of transparency is 1 − opacity.
Premultiplied Alpha Blending
[edit | edit source]There is an important variant of alpha blending: sometimes the fragment color has its alpha component already premultiplied to the color components. (You might think of it as a price that has VAT already included.) In this case, alpha should not be multiplied again (VAT should not be added again) and the correct blending is:
Blend One OneMinusSrcAlpha
which corresponds to:
vec4 result = vec4(1.0) * gl_FragColor + vec4(1.0 - gl_FragColor.a) * pixel_color;
Additive Blending
[edit | edit source]Another example for a blending equation is:
Blend One One
This corresponds to:
vec4 result = vec4(1.0) * gl_FragColor + vec4(1.0) * pixel_color;
which just adds the fragment color to the color in the framebuffer. Note that the alpha component is not used at all; nonetheless, this blending equation is very useful for many kinds of transparent effects; for example, it is often used for particle systems when they represent fire or something else that is transparent and emits light. Additive blending is discussed in more detail in Section “Order-Independent Transparency”.
More examples of blend equations are given in Unity's ShaderLab reference about blending.
Shader Code
[edit | edit source]Here is a simple shader which uses alpha blending to render a green color with opacity 0.3:
Shader "GLSL shader using blending" {
SubShader {
Tags { "Queue" = "Transparent" }
// draw after all opaque geometry has been drawn
Pass {
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend SrcAlpha OneMinusSrcAlpha // use alpha blending
GLSLPROGRAM
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(0.0, 1.0, 0.0, 0.3);
// the fourth component (alpha) is important:
// this is semitransparent green
}
#endif
ENDGLSL
}
}
}
Apart from the blend equation, which has been discussed above, there are only two lines that need more explanation: Tags { "Queue" = "Transparent" } and ZWrite Off.
ZWrite Off deactivates writing to the depth buffer. As explained in Section “Per-Fragment Operations”, the depth buffer keeps the depth of the nearest fragment and discards any fragments that have a larger depth. In the case of a transparent fragment, however, this is not what we want since we can (at least potentially) see through a transparent fragment. Thus, transparent fragments should not occlude other fragments and therefore the writing to the depth buffer is deactivated. See also Unity's ShaderLab reference about culling and depth testing.
The line Tags { "Queue" = "Transparent" } specifies that the meshes using this subshader are rendered after all the opaque meshes were rendered. The reason is partly because we deactivate writing to the depth buffer: one consequence is that transparent fragments can be occluded by opaque fragments even though the opaque fragments are farther away. In order to fix this problem, we first draw all opaque meshes (in Unity´s “opaque queue”) before drawing all transparent meshes (in Unity's “transparent queue”). Whether or not a mesh is considered opaque or transparent depends on the tags of its subshader as specified with the line Tags { "Queue" = "Transparent" }. More details about subshader tags are described in Unity's ShaderLab reference about subshader tags.
It should be mentioned that this strategy of rendering transparent meshes with deactivated writing to the depth buffer does not always solve all problems. It works perfectly if the order in which fragments are blended does not matter; for example, if the fragment color is just added to the pixel color in the framebuffer, the order in which fragments are blended is not important; see Section “Order-Independent Transparency”. However, for other blending equations, e.g. alpha blending, the result will be different depending on the order in which fragments are blended. (If you look through almost opaque green glass at almost opaque red glass you will mainly see green, while you will mainly see red if you look through almost opaque red glass at almost opaque green glass. Similarly, blending almost opaque green color over almost opaque red color will be different from blending almost opaque red color over almost opaque green color.) In order to avoid artifacts, it is therefore advisable to use additive blending or (premultiplied) alpha blending with small opacities (in which case the destination factor DstFactor is close to 1 and therefore alpha blending is close to additive blending).
Including Back Faces
[edit | edit source]The previous shader works well with other objects but it actually doesn't render the “inside” of the object. However, since we can see through the outside of a transparent object, we should also render the inside. As discussed in Section “Cutaways”, the inside can be rendered by deactivating culling with Cull Off. However, if we just deactivate culling, we might get in trouble: as discussed above, it often matters in which order transparent fragments are rendered but without any culling, overlapping triangles from the inside and the outside might be rendered in a random order which can lead to annoying rendering artifacts. Thus, we would like to make sure that the inside (which is usually farther away) is rendered first before the outside is rendered. In Unity's ShaderLab this is achieved by specifying two passes, which are executed for the same mesh in the order in which they are defined:
Shader "GLSL shader using blending (including back faces)" {
SubShader {
Tags { "Queue" = "Transparent" }
// draw after all opaque geometry has been drawn
Pass {
Cull Front // first pass renders only back faces
// (the "inside")
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend SrcAlpha OneMinusSrcAlpha // use alpha blending
GLSLPROGRAM
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(1.0, 0.0, 0.0, 0.3);
// the fourth component (alpha) is important:
// this is semitransparent red
}
#endif
ENDGLSL
}
Pass {
Cull Back // second pass renders only front faces
// (the "outside")
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend SrcAlpha OneMinusSrcAlpha
// standard blend equation "source over destination"
GLSLPROGRAM
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(0.0, 1.0, 0.0, 0.3);
// fourth component (alpha) is important:
// this is semitransparent green
}
#endif
ENDGLSL
}
}
}
In this shader, the first pass uses front-face culling (with Cull Front) to render the back faces (the inside) first. After that the second pass uses back-face culling (with Cull Back) to render the front faces (the outside). This works perfect for convex meshes (closed meshes without dents; e.g. spheres or cubes) and is often a good approximation for other meshes.
Summary
[edit | edit source]Congratulations, you made it through this tutorial! One interesting thing about rendering transparent objects is that it isn't just about blending but also requires knowledge about culling and the depth buffer. Specifically, we have looked at:
- What blending is and how it is specified in Unity.
- How a scene with transparent and opaque objects is rendered and how objects are classified as transparent or opaque in Unity.
- How to render the inside and outside of a transparent object, in particular how to specify two passes in Unity.
Further Reading
[edit | edit source]If you still want to know more
- the OpenGL pipeline, you should read Section “OpenGL ES 2.0 Pipeline”.
- about per-fragment operations in the OpenGL pipeline (e.g. blending and the depth test), you should read Section “Per-Fragment Operations”.
- about front-face and back-face culling, you should read Section “Cutaways”.
- about how to specify culling and the depth buffer functionality in Unity, you should read Unity's ShaderLab reference about culling and depth testing.
- about how to specify blending in Unity, you should read Unity's ShaderLab reference about blending.
- about the render queues in Unity, you should read Unity's ShaderLab reference about subshader tags.
Order-Independent Transparency
[edit | edit source]
This tutorial covers order-independent blending.
It continues the discussion in Section “Transparency” and solves some problems of standard transparency. If you haven't read that tutorial, you should read it first.

Order-Independent Blending
[edit | edit source]As noted in Section “Transparency”, the result of blending often (in particular for standard alpha blending) depends on the order in which triangles are rendered and therefore results in rendering artifacts if the triangles are not sorted from back to front (which they usually aren't). The term “order-independent transparency” describes various techniques to avoid this problem. One of these techniques is order-independent blending, i.e. the use of a blend equation that does not depend on the order in which triangles are rasterized. There two basic possibilities: additive blending and multiplicative blending.
Additive Blending
[edit | edit source]The standard example for additive blending are double exposures as in the images in this section: colors are added such that it is impossible (or at least very hard) to say in which order the photos were taken. Additive blending can be characterized in terms of the blend equation introduced in Section “Transparency”:
vec4 result = SrcFactor * gl_FragColor + DstFactor * pixel_color;
where SrcFactor and DstFactor are determined by a line in Unity's ShaderLab syntax:
Blend {code for SrcFactor} {code for DstFactor}
For additive blending, the code for DstFactor has to be One and the code for SrcFactor must not depend on the pixel color in the framebuffer; i.e., it can be One, SrcColor, SrcAlpha, OneMinusSrcColor, or OneMinusSrcAlpha.
An example is:
Shader "GLSL shader using additive blending" {
SubShader {
Tags { "Queue" = "Transparent" }
// draw after all opaque geometry has been drawn
Pass {
Cull Off // draw front and back faces
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend SrcAlpha One // additive blending
GLSLPROGRAM
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(1.0, 0.0, 0.0, 0.3);
}
#endif
ENDGLSL
}
}
}
Multiplicative Blending
[edit | edit source]An example for multiplicative blending in photography is the use of multiple uniform grey filters: the order in which the filters are put onto a camera doesn't matter for the resulting attenuation of the image. In terms of the rasterization of triangles, the image corresponds to the contents of the framebuffer before the triangles are rasterized, while the filters correspond to the triangles.
When specifying multiplicative blending in Unity with the line
Blend {code for SrcFactor} {code for DstFactor}
the code for SrcFactor has to be Zero and the code for DstFactor must depend on the fragment color; i.e., it can be SrcColor, SrcAlpha, OneMinusSrcColor, or OneMinusSrcAlpha. A typical example for attenuating the background with the opacity specified by the alpha component of fragments would use OneMinusSrcAlpha for the code for DstFactor:
Shader "GLSL shader using multiplicative blending" {
SubShader {
Tags { "Queue" = "Transparent" }
// draw after all opaque geometry has been drawn
Pass {
Cull Off // draw front and back faces
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend Zero OneMinusSrcAlpha // multiplicative blending
// for attenuation by the fragment's alpha
GLSLPROGRAM
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(1.0, 0.0, 0.0, 0.3);
// only A (alpha) is used
}
#endif
ENDGLSL
}
}
}
Complete Shader Code
[edit | edit source]Finally, it makes good sense to combine multiplicative blending for the attenuation of the background and additive blending for the addition of colors of the triangles in one shader by combining the two passes that were presented above. This can be considered an approximation to alpha blending for small opacities, i.e. small values of alpha, if one ignores attenuation of colors of the triangle mesh by itself.
Shader "GLSL shader using order-independent blending" {
SubShader {
Tags { "Queue" = "Transparent" }
// draw after all opaque geometry has been drawn
Pass {
Cull Off // draw front and back faces
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend Zero OneMinusSrcAlpha // multiplicative blending
// for attenuation by the fragment's alpha
GLSLPROGRAM
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(1.0, 0.0, 0.0, 0.3);
// only A (alpha) is used
}
#endif
ENDGLSL
}
Pass {
Cull Off // draw front and back faces
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend SrcAlpha One // additive blending to add colors
GLSLPROGRAM
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(1.0, 0.0, 0.0, 0.3);
}
#endif
ENDGLSL
}
}
}
Note that the order of the two passes is important: first the background is attenuated and then colors are added.
Summary
[edit | edit source]Congratulations, you have reached the end of this tutorial. We have looked at:
- What order-independent transparency and order-independent blending is.
- What the two most important kinds of order-independent blending are (additive and multiplicative).
- How to implement additive and multiplicative blending.
- How to combine two passes for additive and multiplicative blending for an order-independent approximation to alpha blending.
Further Reading
[edit | edit source]If you still want to know more
- about the shader code, you should read Section “Transparency”.
- about another technique for order-independent transparency, namely depth peeling, you could read a technical report by Cass Everitt: “Interactive Order-Independent Transparency”, which is available online.
Silhouette Enhancement
[edit | edit source]
This tutorial covers the transformation of surface normal vectors. It assumes that you are familiar with alpha blending as discussed in Section “Transparency” and with shader properties as discussed in Section “Shading in World Space”.
The objective of this tutorial is to achieve an effect that is visible in the photo to the left: the silhouettes of semitransparent objects tend to be more opaque than the rest of the object. This adds to the impression of a three-dimensional shape even without lighting. It turns out that transformed normals are crucial to obtain this effect.

Silhouettes of Smooth Surfaces
[edit | edit source]In the case of smooth surfaces, points on the surface at silhouettes are characterized by normal vectors that are parallel to the viewing plane and therefore orthogonal to the direction to the viewer. In the figure to the left, the blue normal vectors at the silhouette at the top of the figure are parallel to the viewing plane while the other normal vectors point more in the direction to the viewer (or camera). By calculating the direction to the viewer and the normal vector and testing whether they are (almost) orthogonal to each other, we can therefore test whether a point is (almost) on the silhouette.
More specifically, if V is the normalized (i.e. of length 1) direction to the viewer and N is the normalized surface normal vector, then the two vectors are orthogonal if the dot product is 0: V·N = 0. In practice, this will rarely be the case. However, if the dot product V·N is close to 0, we can assume that the point is close to a silhouette.
Increasing the Opacity at Silhouettes
[edit | edit source]For our effect, we should therefore increase the opacity if the dot product V·N is close to 0. There are various ways to increase the opacity for small dot products between the direction to the viewer and the normal vector. Here is one of them (which actually has a physical model behind it, which is described in Section 5.1 of this publication) to compute the increased opacity from the regular opacity of the material:
It always makes sense to check the extreme cases of an equation like this. Consider the case of a point close to the silhouette: V·N ≈ 0. In this case, the regular opacity will be divided by a small, positive number. (Note that GLSL guarantees to handle the case of division by zero gracefully; thus, we don't have to worry about it.) Therefore, whatever is, the ratio of and a small positive number, will be larger. The function will take care that the resulting opacity is never larger than 1.
On the other hand, for points far away from the silhouette we have V·N ≈ 1. In this case, α' ≈ min(1, α) ≈ α; i.e., the opacity of those points will not change much. This is exactly what we want. Thus, we have just checked that the equation is at least plausible.
Implementing an Equation in a Shader
[edit | edit source]In order to implement an equation like the one for in a shader, the first question should be: Should it be implemented in the vertex shader or in the fragment shader? In some cases, the answer is clear because the implementation requires texture mapping, which is often only available in the fragment shader. In many cases, however, there is no general answer. Implementations in vertex shaders tend to be faster (because there are usually fewer vertices than fragments) but of lower image quality (because normal vectors and other vertex attributes can change abruptly between vertices). Thus, if you are most concerned about performance, an implementation in a vertex shader is probably a better choice. On the other hand, if you are most concerned about image quality, an implementation in a pixel shader might be a better choice. The same trade-off exists between per-vertex lighting (i.e. Gouraud shading, which is discussed in Section “Specular Highlights”) and per-fragment lighting (i.e. Phong shading, which is discussed in Section “Smooth Specular Highlights”).
The next question is: in which coordinate system should the equation be implemented? (See Section “Vertex Transformations” for a description of the standard coordinate systems.) Again, there is no general answer. However, an implementation in world coordinates is often a good choice in Unity because many uniform variables are specified in world coordinates. (In other environments implementations in view coordinates are very common.)
The final question before implementing an equation is: where do we get the parameters of the equation from? The regular opacity is specified (within a RGBA color) by a shader property (see Section “Shading in World Space”). The normal vector gl_Normal is a standard vertex attribute (see Section “Debugging of Shaders”). The direction to the viewer can be computed in the vertex shader as the vector from the vertex position in world space to the camera position in world space _WorldSpaceCameraPos, which is provided by Unity.
Thus, we only have to transform the vertex position and the normal vector into world space before implementing the equation. The transformation matrix _Object2World from object space to world space and its inverse _World2Object are provided by Unity as discussed in Section “Shading in World Space”. The application of transformation matrices to points and normal vectors is discussed in detail in Section “Applying Matrix Transformations”. The basic result is that points and directions are transformed just by multiplying them with the transformation matrix, e.g.:
uniform mat4 _Object2World;
...
vec4 positionInWorldSpace = _Object2World * gl_Vertex;
vec3 viewDirection = _WorldSpaceCameraPos - vec3(positionInWorldSpace);
On the other hand normal vectors are transformed by multiplying them with the transposed inverse transformation matrix. Since Unity provides us with the inverse transformation matrix (which is _World2Object * unity_Scale.w apart from the bottom-right elemen), a better alternative is to multiply the normal vector from the left to the inverse matrix, which is equivalent to multiplying it from the right to the transposed inverse matrix as discussed in Section “Applying Matrix Transformations”:
uniform mat4 _World2Object; // the inverse of _Object2World
// (after multiplication with unity_Scale.w)
uniform vec4 unity_Scale;
...
vec3 normalInWorldSpace = vec3(vec4(gl_Normal, 0.0) * _World2Object
* unity_Scale.w); // corresponds to a multiplication of the
// transposed inverse of _Object2World with gl_Normal
Note that the incorrect bottom-right matrix element is no problem because it is always multiplied with 0. Moreover, the multiplication with unity_Scale.w is unnecessary if the scaling doesn't matter; for example, if we normalize all transformed vectors.
Now we have all the pieces that we need to write the shader.
Shader Code
[edit | edit source]Shader "GLSL silhouette enhancement" {
Properties {
_Color ("Color", Color) = (1, 1, 1, 0.5)
// user-specified RGBA color including opacity
}
SubShader {
Tags { "Queue" = "Transparent" }
// draw after all opaque geometry has been drawn
Pass {
ZWrite Off // don't occlude other objects
Blend SrcAlpha OneMinusSrcAlpha // standard alpha blending
GLSLPROGRAM
uniform vec4 _Color; // define shader property for shaders
// The following built-in uniforms are also defined in
// "UnityCG.glslinc", which could be #included
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
// (apart from the factor unity_Scale.w)
varying vec3 varyingNormalDirection;
// normalized surface normal vector
varying vec3 varyingViewDirection;
// normalized view direction
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object;
// multiplication with unity_Scale.w is unnecessary
// because we normalize transformed vectors
varyingNormalDirection = normalize(
vec3(vec4(gl_Normal, 0.0) * modelMatrixInverse));
varyingViewDirection = normalize(_WorldSpaceCameraPos
- vec3(modelMatrix * gl_Vertex));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection = normalize(varyingViewDirection);
float newOpacity = min(1.0, _Color.a
/ abs(dot(viewDirection, normalDirection)));
gl_FragColor = vec4(vec3(_Color), newOpacity);
}
#endif
ENDGLSL
}
}
}
The assignment to newOpacity is an almost literal translation of the equation
Note that we normalize the varyings varyingNormalDirection and varyingViewDirection in the vertex shader (because we want to interpolate between directions without putting more nor less weight on any of them) and at the begin of the fragment shader (because the interpolation can distort our normalization to a certain degree). However, in many cases the normalization of varyingNormalDirection in the vertex shader is not necessary. Similarly, the normalization of varyingViewDirection in the fragment shader is in most cases unnecessary.
More Artistic Control
[edit | edit source]While the described silhouette enhancement is based on a physical model, it lacks artistic control; i.e., a CG artist cannot easily create a thinner or thicker silhouette than the physical model suggests. To allow for more artistic control, you could introduce another (positive) floating-point number property and take the dot product |V·N| to the power of this number (using the built-in GLSL function pow(float x, float y)) before using it in the equation above. This will allow CG artists to create thinner or thicker silhouettes independently of the opacity of the base color.
Summary
[edit | edit source]Congratulations, you have finished this tutorial. We have discussed:
- How to find silhouettes of smooth surfaces (using the dot product of the normal vector and the view direction).
- How to enhance the opacity at those silhouettes.
- How to implement equations in shaders.
- How to transform points and normal vectors from object space to world space (using the transposed inverse model matrix for normal vectors).
- How to compute the viewing direction (as the difference from the camera position to the vertex position).
- How to interpolate normalized directions (i.e. normalize twice: in the vertex shader and the fragment shader).
- How to provide more artistic control over the thickness of silhouettes .
Further Reading
[edit | edit source]If you still want to know more
- about object space and world space, you should read the description in Section “Vertex Transformations”.
- about how to apply transformation matrices to points, directions and normal vectors, you should read Section “Applying Matrix Transformations”.
- about the basics of rendering transparent objects, you should read Section “Transparency”.
- about uniform variables provided by Unity and shader properties, you should read Section “Shading in World Space”.
- about the mathematics of silhouette enhancement, you could read Section 5.1 of the paper “Scale-Invariant Volume Rendering” by Martin Kraus, published at IEEE Visualization 2005, which is available online.
Diffuse Reflection
[edit | edit source]
This tutorial covers per-vertex diffuse reflection.
It's the first in a series of tutorials about basic lighting in Unity. In this tutorial, we start with diffuse reflection from a single directional light source and then include point light sources and multiple light sources (using multiple passes). Further tutorials cover extensions of this, in particular specular reflection, per-pixel lighting, and two-sided lighting.
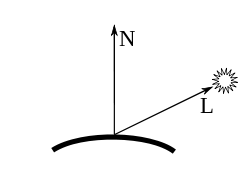
Diffuse Reflection
[edit | edit source]The moon exhibits almost exclusively diffuse reflection (also called Lambertian reflection), i.e. light is reflected into all directions without specular highlights. Other examples of such materials are chalk and matte paper; in fact, any surface that appears dull and matte.
In the case of perfect diffuse reflection, the intensity of the observed reflected light depends on the cosine of the angle between the surface normal vector and the ray of the incoming light. As illustrated in the figure to the left, it is common to consider normalized vectors starting in the point of a surface, where the lighting should be computed: the normalized surface normal vector N is orthogonal to the surface and the normalized light direction L points to the light source.
For the observed diffuse reflected light , we need the cosine of the angle between the normalized surface normal vector N and the normalized direction to the light source L, which is the dot product N·L because the dot product a·b of any two vectors a and b is:
.
In the case of normalized vectors, the lengths |a| and |b| are both 1.
If the dot product N·L is negative, the light source is on the “wrong” side of the surface and we should set the reflection to 0. This can be achieved by using max(0, N·L), which makes sure that the value of the dot product is clamped to 0 for negative dot products. Furthermore, the reflected light depends on the intensity of the incoming light and a material constant for the diffuse reflection: for a black surface, the material constant is 0, for a white surface it is 1. The equation for the diffuse reflected intensity is then:
For colored light, this equation applies to each color component (e.g. red, green, and blue). Thus, if the variables , , and denote color vectors and the multiplications are performed component-wise (which they are for vectors in GLSL), this equation also applies to colored light. This is what we actually use in the shader code.
Shader Code for One Directional Light Source
[edit | edit source]If we have only one directional light source, the shader code for implementing the equation for is relatively small. In order to implement the equation, we follow the questions about implementing equations, which were discussed in Section “Silhouette Enhancement”:
- Should the equation be implemented in the vertex shader or the fragment shader? We try the vertex shader here. In Section “Smooth Specular Highlights”, we will look at an implementation in the fragment shader.
- In which coordinate system should the equation be implemented? We try world space by default in Unity. (Which turns out to be a good choice here because Unity provides the light direction in world space.)
- Where do we get the parameters from? The answer to this is a bit longer:
We use a shader property (see Section “Shading in World Space”) to let the user specify the diffuse material color . We can get the direction to the light source in world space from the Unity-specific uniform _WorldSpaceLightPos0 and the light color from the Unity-specific uniform _LightColor0. As mentioned in Section “Shading in World Space”, we have to tag the shader pass with Tags {"LightMode" = "ForwardBase"} to make sure that these uniforms have the correct values. (Below we will discuss what this tag actually means.) We get the surface normal vector in object coordinates from the attribute gl_Normal. Since we implement the equation in world space, we have to convert the surface normal vector from object space to world space as discussed in Section “Silhouette Enhancement”.
The shader code then looks like this:
Shader "GLSL per-vertex diffuse lighting" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// make sure that all uniforms are correctly set
GLSLPROGRAM
uniform vec4 _Color; // shader property specified by users
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 color;
// the diffuse lighting computed in the vertex shader
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(
vec3(vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 lightDirection = normalize(
vec3(_WorldSpaceLightPos0));
vec3 diffuseReflection = vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
color = vec4(diffuseReflection, 1.0);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = color;
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Diffuse"
}
When you use this shader, make sure that there is only one light source in the scene, which has to be directional. If there is no light source, you can create a directional light source by selecting Game Object > Create Other > Directional Light from the main menu. Also, make sure that the “Forward Rendering Path” is active by selecting Edit > Project Settings > Player and then in the Inspector View the Per-Platform Settings > Other Settings > Rendering > Rendering Path should be set to Forward. (See below for more details about the “Forward Rendering Path”.)
Fallback Shaders
[edit | edit source]The line Fallback "Diffuse" in the shader code defines a built-in fallback shader in case Unity doesn't find an appropriate subshader. For our example, Unity would use the fallback shader if it doesn't use the “forward rendering path” (see below) or if it couldn't compile the shader code. By choosing the specific name “_Color” for our shader property, we make sure that this built-in fallback shader can also access it. The source code of the built-in shaders is available at Unity's website. Inspection of this source code appears to be the only way to determine a suitable fallback shader and the names of the properties that it is using.
As mentioned, Unity will also use the fallback shader if there is a compile error in the shader code. In this case, the error is only be reported in the Inspector View of the shader; thus, it might be difficult to understand that the fallback shader is being used. Therefore, it is usually a good idea to comment the fallback instruction out during development of a shader but include it in the final version for better compatibility.
Shader Code for Multiple Directional (Pixel) Lights
[edit | edit source]So far, we have only considered a single light source. In order to handle multiple light sources, Unity chooses various techniques depending on the rendering and quality settings. In the tutorials here, we will only cover the “Forward Rendering Path”. In order to choose it, select Edit > Project Settings > Player and then in the Inspector View set Per-Platform Settings > Other Settings > Rendering > Rendering Path to Forward. (Moreover, all cameras should be configured to use the player settings, which they are by default.)
In this tutorial we consider only Unity's so-called pixel lights. For the first pixel light (which always is a directional light), Unity calls the shader pass tagged with Tags { "LightMode" = "ForwardBase" } (as in our code above). For each additional pixel light, Unity calls the shader pass tagged with Tags { "LightMode" = "ForwardAdd" }. In order to make sure that all lights are rendered as pixel lights, you have to make sure that the quality settings allow for enough pixel lights: Select Edit > Project Settings > Quality and then increase the number labeled Pixel Light Count in any of the quality settings that you use. If there are more light sources in the scene than pixel light count allows for, Unity renders only the most important lights as pixel lights. Alternatively, you can set the Render Mode of all light sources to Important in order to render them as pixel lights. (See Section “Multiple Lights” for a discussion of the less important vertex lights.)
Our shader code so far is OK for the ForwardBase pass. For the ForwardAdd pass, we need to add the reflected light to the light that is already stored in the framebuffer. To this end, we just have to configure the blending to add the new fragment color (gl_FragColor) to the color in the framebuffer. As discussed in Section “Transparency”, this is achieved by an additive blend equation, which is specified by this line:
Blend One One
Blending automatically clamps all results between 0 and 1; thus, we don't have to worry about colors or alpha values greater than 1.
All in all, our new shader for multiple directional lights becomes:
Shader "GLSL per-vertex diffuse lighting" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for first light source
GLSLPROGRAM
uniform vec4 _Color; // shader property specified by users
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 color;
// the diffuse lighting computed in the vertex shader
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(
vec3(vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 lightDirection = normalize(
vec3(_WorldSpaceLightPos0));
vec3 diffuseReflection = vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
color = vec4(diffuseReflection, 1.0);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = color;
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
uniform vec4 _Color; // shader property specified by users
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 color;
// the diffuse lighting computed in the vertex shader
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(
vec3(vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 lightDirection = normalize(
vec3(_WorldSpaceLightPos0));
vec3 diffuseReflection = vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
color = vec4(diffuseReflection, 1.0);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = color;
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Diffuse"
}
This appears to be a rather long shader; however, both passes are identical apart from the tag and the Blend setting in the ForwardAdd pass.
Changes for a Point Light Source
[edit | edit source]In the case of a directional light source _WorldSpaceLightPos0 specifies the direction from where light is coming. In the case of a point light source (or a spot light source), however, _WorldSpaceLightPos0 specifies the position of the light source in world space and we have to compute the direction to the light source as the difference vector from the position of the vertex in world space to the position of the light source. Since the 4th coordinate of a point is 1 and the 4th coordinate of a direction is 0, we can easily distinguish between the two cases:
vec3 lightDirection;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
lightDirection = normalize(
vec3(_WorldSpaceLightPos0 - modelMatrix * gl_Vertex));
}
While there is no attenuation of light for directional light sources, we should add some attenuation with distance to point and spot light source. As light spreads out from a point in three dimensions, it's covering ever larger virtual spheres at larger distances. Since the surface of these spheres increases quadratically with increasing radius and the total amount of light per sphere is the same, the amount of light per area decreases quadratically with increasing distance from the point light source. Thus, we should divide the intensity of the light source by the squared distance to the vertex.
Since a quadratic attenuation is rather rapid, we use a linear attenuation with distance, i.e. we divide the intensity by the distance instead of the squared distance. The code could be:
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource = vec3(_WorldSpaceLightPos0
- modelMatrix * gl_Vertex);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
The factor attenuation should then be multiplied with _LightColor0 to compute the incoming light; see the shader code below. Note that spot light sources have additional features, which are beyond the scope of this tutorial.
Also note that this code is unlikely to give you the best performance because any if is usually quite costly. Since _WorldSpaceLightPos0.w is either 0 or 1, it is actually not too hard to rewrite the code to avoid the use of if and optimize a bit further:
vec3 vertexToLightSource = vec3(_WorldSpaceLightPos0
- modelMatrix * gl_Vertex * _WorldSpaceLightPos0.w);
float one_over_distance =
1.0 / length(vertexToLightSource);
float attenuation =
mix(1.0, one_over_distance, _WorldSpaceLightPos0.w);
vec3 lightDirection =
vertexToLightSource * one_over_distance;
However, we will use the version with if for clarity. (“Keep it simple, stupid!”)
The complete shader code for multiple directional and point lights is:
Shader "GLSL per-vertex diffuse lighting" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for first light source
GLSLPROGRAM
uniform vec4 _Color; // shader property specified by users
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 color;
// the diffuse lighting computed in the vertex shader
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(
vec3(vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource = vec3(_WorldSpaceLightPos0
- modelMatrix * gl_Vertex);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
color = vec4(diffuseReflection, 1.0);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = color;
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
uniform vec4 _Color; // shader property specified by users
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 color;
// the diffuse lighting computed in the vertex shader
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(
vec3(vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource = vec3(_WorldSpaceLightPos0
- modelMatrix * gl_Vertex);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
color = vec4(diffuseReflection, 1.0);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = color;
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Diffuse"
}
Note that the light source in the ForwardBase pass always is a directional light; thus, the code for the first pass could actually be simplified. On the other hand, using the same GLSL code for both passes, makes it easier to copy & paste the code from one pass to the other in case we have to edit the shader code.
If there is a problem with the shader, remember to activate the “Forward Rendering Path” by selecting Edit > Project Settings > Player and then in the Inspector View set Per-Platform Settings > Other Settings > Rendering > Rendering Path to Forward.
Changes for a Spotlight
[edit | edit source]Unity implements spotlights with the help of cookie textures as described in Section “Cookies”; however, this is somewhat advanced. Here, we treat spotlights as if they were point lights.
Summary
[edit | edit source]Congratulations! You just learned how Unity's per-pixel lights work. This is essential for the following tutorials about more advanced lighting. We have also seen:
- What diffuse reflection is and how to describe it mathematically.
- How to implement diffuse reflection for a single directional light source in a shader.
- How to extend the shader for point light sources with linear attenuation.
- How to further extend the shader to handle multiple per-pixel lights.
Further Reading
[edit | edit source]If you still want to know more
- about transforming normal vectors into world space, you should read Section “Shading in World Space”.
- about uniform variables provided by Unity and shader properties, you should read Section “Shading in World Space”.
- about (additive) blending, you should read Section “Transparency”.
- about pass tags in Unity (e.g.
ForwardBaseorForwardAdd), you should read Unity's ShaderLab reference about pass tags. - about how Unity processes light sources in general, you should read Unity's manual about rendering paths.
Specular Highlights
[edit | edit source]
This tutorial covers per-vertex lighting (also known as Gouraud shading) using the Phong reflection model.
It extends the shader code in Section “Diffuse Reflection” by two additional terms: ambient lighting and specular reflection. Together, the three terms constitute the Phong reflection model. If you haven't read Section “Diffuse Reflection”, this would be a very good opportunity to read it.
Ambient Light
[edit | edit source]Consider the painting by Caravaggio to the left. While large parts of the white shirt are in shadows, no part of it is completely black. Apparently there is always some light being reflected from walls and other objects to illuminate everything in the scene — at least to a certain degree. In the Phong reflection model, this effect is taken into account by ambient lighting, which depends on a general ambient light intensity and the material color for diffuse reflection. In an equation for the intensity of ambient lighting :
Analogously to the equation for diffuse reflection in Section “Diffuse Reflection”, this equation can also be interpreted as a vector equation for the red, green, and blue components of light.
In Unity, the ambient light is specified by choosing Edit > Render Settings(In Unity5 by choosing Window > Lighting) from the main menu. In a GLSL shader in Unity, this color is always available as gl_LightModel.ambient, which is one of the pre-defined uniforms of the OpenGL compatibility profile mentioned in Section “Shading in World Space”.

Specular Highlights
[edit | edit source]If you have a closer look at Caravaggio's painting, you will see several specular highlights: on the nose, on the hair, on the lips, on the lute, on the violin, on the bow, on the fruits, etc. The Phong reflection model includes a specular reflection term that can simulate such highlights on shiny surfaces; it even includes a parameter to specify a shininess of the material. The shininess specifies how small the highlights are: the shinier, the smaller the highlights.
A perfectly shiny surface will reflect light from the light source only in the geometrically reflected direction R. For less than perfectly shiny surfaces, light is reflected to directions around R: the smaller the shininess, the wider the spreading. Mathematically, the normalized reflected direction R is defined by:
for a normalized surface normal vector N and a normalized direction to the light source L. In GLSL, the function vec3 reflect(vec3 I, vec3 N) (or vec4 reflect(vec4 I, vec4 N)) computes the same reflected vector but for the direction I from the light source to the point on the surface. Thus, we have to negate our direction L to use this function.
The specular reflection term computes the specular reflection in the direction of the viewer V. As discussed above, the intensity should be large if V is close to R, where “closeness” is parametrized by the shininess . In the Phong reflection model, the cosine of the angle between R and V to the -th power is used to generate highlights of different shininess. Similarly to the case of the diffuse reflection, we should clamp negative cosines to 0. Furthermore, the specular term requires a material color for the specular reflection, which is usually just white such that all highlights have the color of the incoming light . For example, all highlights in Caravaggio's painting are white. The specular term of the Phong reflection model is then:
Analogously to the case of the diffuse reflection, the specular term should be ignored if the light source is on the “wrong” side of the surface; i.e., if the dot product N·L is negative.
Shader Code
[edit | edit source]The shader code for the ambient lighting is straightforward with a component-wise vector-vector product:
vec3 ambientLighting = vec3(gl_LightModel.ambient) * vec3(_Color);
For the implementation of the specular reflection, we require the direction to the viewer in world space, which we can compute as the difference between the camera position and the vertex position (both in world space). The camera position in world space is provided by Unity in the uniform _WorldSpaceCameraPos; the vertex position can be transformed to world space as discussed in Section “Diffuse Reflection”. The equation of the specular term in world space could then be implemented like this:
vec3 viewDirection = normalize(vec3(
vec4(_WorldSpaceCameraPos, 1.0)
- modelMatrix * gl_Vertex));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
This code snippet uses the same variables as the shader code in Section “Diffuse Reflection” and additionally the user-specified properties _SpecColor and _Shininess. (The names were specifically chosen such that the fallback shader can access them; see the discussion in Section “Diffuse Reflection”.) pow(a, b) computes .
If the ambient lighting is added to the first pass (we only need it once) and the specular reflection is added to both passes of the full shader of Section “Diffuse Reflection”, it looks like this:
Shader "GLSL per-vertex lighting" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 color;
// the Phong lighting computed in the vertex shader
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 viewDirection = normalize(vec3(
vec4(_WorldSpaceCameraPos, 1.0)
- modelMatrix * gl_Vertex));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource = vec3(_WorldSpaceLightPos0
- modelMatrix * gl_Vertex);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
color = vec4(ambientLighting + diffuseReflection
+ specularReflection, 1.0);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = color;
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 color;
// the diffuse lighting computed in the vertex shader
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 viewDirection = normalize(vec3(
vec4(_WorldSpaceCameraPos, 1.0)
- modelMatrix * gl_Vertex));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource = vec3(_WorldSpaceLightPos0
- modelMatrix * gl_Vertex);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
// vec3 ambientLighting =
// vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
color = vec4(diffuseReflection + specularReflection, 1.0);
// no ambient lighting in this pass
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = color;
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Summary
[edit | edit source]Congratulation, you just learned how to implement the Phong reflection model. In particular, we have seen:
- What the ambient lighting in the Phong reflection model is.
- What the specular reflection term in the Phong reflection model is.
- How these terms can be implemented in GLSL in Unity.
Further Reading
[edit | edit source]If you still want to know more
- about the shader code, you should read Section “Diffuse Reflection”.
Two-Sided Surfaces
[edit | edit source]
This tutorial covers two-sided per-vertex lighting.
It's part of a series of tutorials about basic lighting in Unity. In this tutorial, we extend Section “Specular Highlights” to render two-sided surfaces. If you haven't read Section “Specular Highlights”, this would be a very good time to read it.

Two-Sided Lighting
[edit | edit source]As shown by the figure of the algebraic surface, it's sometimes useful to apply different colors to the two sides of a surface. In Section “Cutaways”, we have seen how a fragment shader can use the built-in variable gl_FrontFacing to determine whether a fragment is part of a front-facing or a back-facing triangle. Can a vertex shader also determine whether it is part of a front-facing or a back-facing triangle? The answer is a clear: no! One reason is that the same vertex can be part of a front-facing and a back-facing triangle at the same time; thus, whatever decision is made in the vertex shader, it is potentially wrong for some triangles. If you want a simple rule to remember: “Fragments are either front-facing or back-facing. Vertices are bi.”
Thus, two-sided per-vertex lighting has to let the fragment shader determine, whether the front or the back material color should be applied. For example, with this fragment shader:
#ifdef FRAGMENT
varying vec4 frontColor; // color for front face
varying vec4 backColor; // color for back face
void main()
{
if (gl_FrontFacing) // is the fragment part of a front face?
{
gl_FragColor = frontColor;
}
else // fragment is part of a back face
{
gl_FragColor = backColor;
}
}
#endif
On the other hand, this means that the vertex shader has to compute the surface lighting twice: for a front face and for a back face. Fortunately, this is usually still less work than computing the surface lighting for each fragment.
Shader Code
[edit | edit source]The shader code for two-sided per-vertex lighting is a straightforward extension of the code in Section “Specular Highlights”. It requires two sets of material parameters (front and back) and deactivates culling. The vertex shader computes two colors, one for front faces and one for back faces using the negated normal vector and the second set of material parameters. Then the fragment shader decides which one to apply.
Shader "GLSL two-sided per-vertex lighting" {
Properties {
_Color ("Front Material Diffuse Color", Color) = (1,1,1,1)
_SpecColor ("Front Material Specular Color", Color) = (1,1,1,1)
_Shininess ("Front Material Shininess", Float) = 10
_BackColor ("Back Material Diffuse Color", Color) = (1,1,1,1)
_BackSpecColor ("Back Material Specular Color", Color)
= (1,1,1,1)
_BackShininess ("Back Material Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
Cull Off // render front faces and back faces
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _BackColor;
uniform vec4 _BackSpecColor;
uniform float _BackShininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 frontColor;
// lighting of front faces computed in the vertex shader
varying vec4 backColor;
// lighting of back faces computed in the vertex shader
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(vec3(vec4(gl_Normal, 0.0)
* modelMatrixInverse));
vec3 viewDirection = normalize(vec3(
vec4(_WorldSpaceCameraPos, 1.0)
- modelMatrix * gl_Vertex));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource = vec3(_WorldSpaceLightPos0
- modelMatrix * gl_Vertex);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
// Computation of lighting for front faces
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
frontColor = vec4(ambientLighting + diffuseReflection
+ specularReflection, 1.0);
// Computation of lighting for back faces
// (uses negative normalDirection and back material colors)
vec3 backAmbientLighting =
vec3(gl_LightModel.ambient) * vec3(_BackColor);
vec3 backDiffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_BackColor)
* max(0.0, dot(-normalDirection, lightDirection));
vec3 backSpecularReflection;
if (dot(-normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
backSpecularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
backSpecularReflection =
attenuation * vec3(_LightColor0)
* vec3(_BackSpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, -normalDirection),
viewDirection)), _BackShininess);
}
backColor = vec4(backAmbientLighting +
backDiffuseReflection + backSpecularReflection, 1.0);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
if (gl_FrontFacing)
// is the fragment part of a front face?
{
gl_FragColor = frontColor;
}
else // fragment is part of a back face
{
gl_FragColor = backColor;
}
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
Cull Off // render front faces and back faces
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _BackColor;
uniform vec4 _BackSpecColor;
uniform float _BackShininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 frontColor;
// lighting of front faces computed in the vertex shader
varying vec4 backColor;
// lighting of back faces computed in the vertex shader
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 viewDirection = normalize(vec3(
vec4(_WorldSpaceCameraPos, 1.0)
- modelMatrix * gl_Vertex));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource = vec3(_WorldSpaceLightPos0
- modelMatrix * gl_Vertex);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
// Computation of lighting for front faces
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
frontColor = vec4(diffuseReflection
+ specularReflection, 1.0);
// Computation of lighting for back faces
// (uses negative normalDirection and back material colors)
vec3 backDiffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_BackColor)
* max(0.0, dot(-normalDirection, lightDirection));
vec3 backSpecularReflection;
if (dot(-normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
backSpecularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
backSpecularReflection =
attenuation * vec3(_LightColor0)
* vec3(_BackSpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, -normalDirection),
viewDirection)), _BackShininess);
}
backColor = vec4(backDiffuseReflection
+ backSpecularReflection, 1.0);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
if (gl_FrontFacing)
// is the fragment part of a front face?
{
gl_FragColor = frontColor;
}
else // fragment is part of a back face
{
gl_FragColor = backColor;
}
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Again, this code consists of two passes, where the second pass is the same as the first apart from the additive blending and the missing ambient color.
Summary
[edit | edit source]Congratulations, you made it to the end of this short tutorial with a long shader. We have seen:
- Why a vertex shader cannot distinguish between front-facing and back-facing vertices (because the same vertex might be part of a front-facing and a back-facing triangles).
- How to compute lighting for front faces and for back faces in the vertex shader.
- How to let the fragment shader decide which color to apply.
Further Reading
[edit | edit source]If you still want to know more
- about the shader version for single-sided surfaces, you should read Section “Specular Highlights”.
- about front-facing and back-facing triangles in GLSL, you should read Section “Cutaways”.
Smooth Specular Highlights
[edit | edit source]

This tutorial covers per-pixel lighting (also known as Phong shading).
It is based on Section “Specular Highlights”. If you haven't read that tutorial yet, you should read it first. The main disadvantage of per-vertex lighting (i.e. of computing the surface lighting for each vertex and then interpolating the vertex colors) is the limited quality, in particular for specular highlights as demonstrated by the figure to the left. The remedy is per-pixel lighting which computes the lighting for each fragment based on an interpolated normal vector. While the resulting image quality is considerably higher, the performance costs are also significant.
Per-Pixel Lighting (Phong Shading)
[edit | edit source]Per-pixel lighting is also known as Phong shading (in contrast to per-vertex lighting, which is also known as Gouraud shading). This should not be confused with the Phong reflection model (also called Phong lighting), which computes the surface lighting by an ambient, a diffuse, and a specular term as discussed in Section “Specular Highlights”.
The key idea of per-pixel lighting is easy to understand: normal vectors and positions are interpolated for each fragment and the lighting is computed in the fragment shader.
Shader Code
[edit | edit source]Apart from optimizations, implementing per-pixel lighting based on shader code for per-vertex lighting is straightforward: the lighting computation is moved from the vertex shader to the fragment shader and the vertex shader has to write the attributes required for the lighting computation to varyings. The fragment shader then uses these varyings to compute the lighting (instead of the attributes that the vertex shader used). That's about it.
In this tutorial, we adapt the shader code from Section “Specular Highlights” to per-pixel lighting. The result looks like this:
Shader "GLSL per-pixel lighting" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(ambientLighting + diffuseReflection
+ specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor =
vec4(diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Note that the vertex shader writes a normalized vector to varyingNormalDirection in order to make sure that all directions are weighted equally in the interpolation. The fragment shader normalizes it again because the interpolated directions are no longer normalized.
Summary
[edit | edit source]Congratulations, now you know how per-pixel Phong lighting works. We have seen:
- Why the quality provided by per-vertex lighting is sometimes insufficient (in particular because of specular highlights).
- How per-pixel lighting works and how to implement it based on a shader for per-vertex lighting.
Further Reading
[edit | edit source]If you still want to know more
- about the shader version for per-vertex lighting, you should read Section “Specular Highlights”.
Two-Sided Smooth Surfaces
[edit | edit source]
This tutorial covers two-sided per-pixel lighting (i.e. two-sided Phong shading).
Here we combine the per-pixel lighting discussed in Section “Smooth Specular Highlights” with the two-sided lighting discussed in Section “Two-Sided Surfaces”.
Shader Coder
[edit | edit source]The required changes to the code of Section “Smooth Specular Highlights” are: new properties for the back material, deactivation of culling, new local variables for the material parameters in the fragment shader, which are set either to the front material parameters or the back material parameters according to gl_FrontFacing. Also, the surface normal vector is negated in case a back face is rendered. It's actually quite straightforward. The code looks like this:
Shader "GLSL two-sided per-pixel lighting" {
Properties {
_Color ("Front Material Diffuse Color", Color) = (1,1,1,1)
_SpecColor ("Front Material Specular Color", Color) = (1,1,1,1)
_Shininess ("Front Material Shininess", Float) = 10
_BackColor ("Back Material Diffuse Color", Color) = (1,1,1,1)
_BackSpecColor ("Back Material Specular Color", Color)
= (1,1,1,1)
_BackShininess ("Back Material Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
Cull Off
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _BackColor;
uniform vec4 _BackSpecColor;
uniform float _BackShininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec4 diffuseColor;
vec4 specularColor;
float shininess;
if (gl_FrontFacing)
{
diffuseColor = _Color;
specularColor = _SpecColor;
shininess = _Shininess;
}
else
{
diffuseColor = _BackColor;
specularColor = _BackSpecColor;
shininess = _BackShininess;
normalDirection = -normalDirection;
}
vec3 viewDirection = normalize(
_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(diffuseColor);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(diffuseColor)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(specularColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), shininess);
}
gl_FragColor = vec4(ambientLighting + diffuseReflection
+ specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
Cull Off
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _BackColor;
uniform vec4 _BackSpecColor;
uniform float _BackShininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec4 diffuseColor;
vec4 specularColor;
float shininess;
if (gl_FrontFacing)
{
diffuseColor = _Color;
specularColor = _SpecColor;
shininess = _Shininess;
}
else
{
diffuseColor = _BackColor;
specularColor = _BackSpecColor;
shininess = _BackShininess;
normalDirection = -normalDirection;
}
vec3 viewDirection = normalize(
_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(diffuseColor)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(specularColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), shininess);
}
gl_FragColor =
vec4(diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
As always, the only difference between the two passes is the lack of ambient lighting and the additive blending in the second pass.
Summary
[edit | edit source]Congratulations, you have reached the end of this short tutorial. We have seen:
- How two-sided surfaces can be rendered with per-pixel lighting.
Further Reading
[edit | edit source]If you still want to know more
- about the shader version for single-sided per-pixel lighting, you should read Section “Smooth Specular Highlights”.
- about the shader version for two-sided per-vertex lighting, you should read Section “Two-Sided Surfaces”.
Multiple Lights
[edit | edit source]
This tutorial covers lighting by multiple light sources in one pass. In particular, it covers Unity's so-called “vertex lights” in the ForwardBase pass.
This tutorial is an extension of Section “Smooth Specular Highlights”. If you haven't read that tutorial, you should read it first.
Multiple Lights in One Pass
[edit | edit source]As discussed in Section “Diffuse Reflection”, Unity's forward rendering path uses separate passes for the most important light sources. These are called “pixel lights” because the built-in shaders render them with per-pixel lighting. All light sources with the Render Mode set to Important are rendered as pixel lights. If the Pixel Light Count of the Quality project settings allows for more pixel lights, then some of the light sources with Render Mode set to Auto are also rendered as pixel lights. What happens to the other light sources? The built-in shaders of Unity render four additional lights as vertex lights in the ForwardBase pass. As the name indicates, the built-in shaders render these lights with per-vertex lighting. This is what this tutorial is about. (Further lights are approximated by spherical harmonic lighting, which is not covered here.)
Unfortunately, it is somewhat unclear how to access the four vertex lights (i.e. their positions and colors). Here is, what appears to work in Unity 3.4 on Windows and MacOS X:
// Built-in uniforms for "vertex lights"
uniform vec4 unity_LightColor[4];
// array of the colors of the 4 light sources
uniform vec4 unity_4LightPosX0;
// x coordinates of the 4 light sources in world space
uniform vec4 unity_4LightPosY0;
// y coordinates of the 4 light sources in world space
uniform vec4 unity_4LightPosZ0;
// z coordinates of the 4 light sources in world space
uniform vec4 unity_4LightAtten0;
// scale factors for attenuation with squared distance
// uniform vec4 unity_LightPosition[4] is apparently not
// always correctly set in Unity 3.4
// uniform vec4 unity_LightAtten[4] is apparently not
// always correctly set in Unity 3.4
Depending on your platform and version of Unity you might have to use unity_LightPosition[4] instead of unity_4LightPosX0, unity_4LightPosY0, and unity_4LightPosZ0. Similarly, you might have to use unity_LightAtten[4] instead of unity_4LightAtten0. Note what's not available: neither any cookie texture nor the transformation to light space (and therefore neither the direction of spotlights). Also, no 4th component of the light positions is available; thus, it is unclear whether a vertex light is a directional light, a point light, or a spotlight.
Here, we follow Unity's built-in shaders and only compute the diffuse reflection by vertex lights using per-vertex lighting. This can be computed with the following for-loop inside the vertex shader:
vertexLighting = vec3(0.0, 0.0, 0.0);
for (int index = 0; index < 4; index++)
{
vec4 lightPosition = vec4(unity_4LightPosX0[index],
unity_4LightPosY0[index],
unity_4LightPosZ0[index], 1.0);
vec3 vertexToLightSource =
vec3(lightPosition - position);
vec3 lightDirection = normalize(vertexToLightSource);
float squaredDistance =
dot(vertexToLightSource, vertexToLightSource);
float attenuation = 1.0 / (1.0 +
unity_4LightAtten0[index] * squaredDistance);
vec3 diffuseReflection =
attenuation * vec3(unity_LightColor[index])
* vec3(_Color) * max(0.0,
dot(varyingNormalDirection, lightDirection));
vertexLighting = vertexLighting + diffuseReflection;
}
The total diffuse lighting by all vertex lights is accumulated in vertexLighting by initializing it to black and then adding the diffuse reflection of each vertex light to the previous value of vertexLighting at the end of the for-loop. A for-loop should be familiar to any C/C++/Java/JavaScript programmer. Note that for-loops are sometimes severely limited; in particular the limits (here: 0 and 4) have to be constants in Unity, i.e. you cannot even use uniforms to determine the limits. (The technical reason is that the limits have to be known at compile time in order to “un-roll” the loop.)
This is more or less how vertex lights are computed in Unity's built-in shaders. However, remember that nothing would stop you from computing specular reflection or per-pixel lighting with these “vertex lights”.
Complete Shader Code
[edit | edit source]In the context of the shader code from Section “Smooth Specular Highlights”, the complete shader code is:
Shader "GLSL per-pixel lighting with vertex lights" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" } // pass for
// 4 vertex lights, ambient light & first pixel light
GLSLPROGRAM
#pragma multi_compile_fwdbase
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
// Built-in uniforms for "vertex lights"
uniform vec4 unity_LightColor[4];
uniform vec4 unity_4LightPosX0;
// x coordinates of the 4 light sources in world space
uniform vec4 unity_4LightPosY0;
// y coordinates of the 4 light sources in world space
uniform vec4 unity_4LightPosZ0;
// z coordinates of the 4 light sources in world space
uniform vec4 unity_4LightAtten0;
// scale factors for attenuation with squared distance
// Varyings
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
varying vec3 vertexLighting;
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
// Diffuse reflection by four "vertex lights"
vertexLighting = vec3(0.0, 0.0, 0.0);
#ifdef VERTEXLIGHT_ON
for (int index = 0; index < 4; index++)
{
vec4 lightPosition = vec4(unity_4LightPosX0[index],
unity_4LightPosY0[index],
unity_4LightPosZ0[index], 1.0);
vec3 vertexToLightSource =
vec3(lightPosition - position);
vec3 lightDirection = normalize(vertexToLightSource);
float squaredDistance =
dot(vertexToLightSource, vertexToLightSource);
float attenuation = 1.0 / (1.0 +
unity_4LightAtten0[index] * squaredDistance);
vec3 diffuseReflection =
attenuation * vec3(unity_LightColor[index])
* vec3(_Color) * max(0.0,
dot(varyingNormalDirection, lightDirection));
vertexLighting = vertexLighting + diffuseReflection;
}
#endif
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(vertexLighting + ambientLighting
+ diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional "pixel lights"
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
// Varyings
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(diffuseReflection
+ specularReflection, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
The use of #pragma multi_compile_fwdbase and #ifdef VERTEXLIGHT_ON ... #endif appears to be necessary to make sure that no vertex lighting is computed when Unity doesn't provide the data.
Summary
[edit | edit source]Congratulations, you have reached the end of this tutorial. We have seen:
- How Unity's vertex lights are specified.
- How a for-loop can be used in GLSL to compute the lighting of multiple lights in one pass.
Further Reading
[edit | edit source]If you still want to know more
- about other parts of the shader code, you should read Section “Smooth Specular Highlights”.
- about Unity's forward rendering path and what is computed in the
ForwardBasepass, you should read Unity's reference about forward rendering.
Textured Spheres
[edit | edit source]
This tutorial introduces texture mapping.
It's the first in a series of tutorials about texturing in GLSL shaders in Unity. In this tutorial, we start with a single texture map on a sphere. More specifically, we map an image of the Earth's surface onto a sphere. Based on this, further tutorials cover topics such as lighting of textured surfaces, transparent textures, multitexturing, gloss mapping, etc.


Texture Mapping
[edit | edit source]The basic idea of “texture mapping” (or “texturing”) is to map an image (i.e. a “texture” or a “texture map”) onto a triangle mesh; in other words, to put a flat image onto the surface of a three-dimensional shape.
To this end, “texture coordinates” are defined, which simply specify the position in the texture (i.e. image). The horizontal coordinate is officially called S and the vertical coordinate T. However, it is very common to refer to them as x and y. In animation and modeling tools, texture coordinates are usually called U and V.
In order to map the texture image to a mesh, every vertex of the mesh is given a pair of texture coordinates. (This process (and the result) is sometimes called “UV mapping” since each vertex is mapped to a point in the UV-space.) Thus, every vertex is mapped to a point in the texture image. The texture coordinates of the vertices can then be interpolated for each point of any triangle between three vertices and thus every point of all triangles of the mesh can have a pair of (interpolated) texture coordinates. These texture coordinates map each point of the mesh to a specific position in the texture map and therefore to the color at this position. Thus, rendering a texture-mapped mesh consists of two steps for all visible points: interpolation of texture coordinates and a look-up of the color of the texture image at the position specified by the interpolated texture coordinates.
In OpenGL, any valid floating-point number is a valid texture coordinate. However, when the GPU is asked to look up a pixel (or “texel”) of a texture image (e.g. with the “texture2D” instruction described below), it will internally map the texture coordinates to the range between 0 and 1 in a way depending on the “Wrap Mode” that is specified when importing the texture: wrap mode “repeat” basically uses the fractional part of the texture coordinates to determine texture coordinates in the range between 0 and 1. On the other hand, wrap mode “clamp” clamps the texture coordinates to this range. These internal texture coordinates in the range between 0 and 1 are then used to determine the position in the texture image: specifies the lower, left corner of the texture image; the lower, right corner; the upper, left corner; etc.
Texturing a Sphere in Unity
[edit | edit source]To map the image of the Earth's surface onto a sphere in Unity, you first have to import the image into Unity. Click the image until you get to a larger version and save it (usually with a right-click) to your computer (remember where you saved it). Then switch to Unity and choose Assets > Import New Asset... from the main menu. Choose the image file and click on Import in the file selector box. The imported texture image should appear in the Project View. By selecting it there, details about the way it is imported appear (and can be changed) in the Inspector View.
Now create a sphere, a material, and a shader, and attach the shader to the material and the material to the sphere as described in Section “Minimal Shader”. The shader code should be:
Shader "GLSL shader with single texture" {
Properties {
_MainTex ("Texture Image", 2D) = "white" {}
// a 2D texture property that we call "_MainTex", which should
// be labeled "Texture Image" in Unity's user interface.
// By default we use the built-in texture "white"
// (alternatives: "black", "gray" and "bump").
}
SubShader {
Pass {
GLSLPROGRAM
uniform sampler2D _MainTex;
// a uniform variable referring to the property above
// (in fact, this is just a small integer specifying a
// "texture unit", which has the texture image "bound"
// to it; Unity takes care of this).
varying vec4 textureCoordinates;
// the texture coordinates at the vertices,
// which are interpolated for each fragment
#ifdef VERTEX
void main()
{
textureCoordinates = gl_MultiTexCoord0;
// Unity provides default longitude-latitude-like
// texture coordinates at all vertices of a
// sphere mesh as the attribute "gl_MultiTexCoord0".
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor =
texture2D(_MainTex, vec2(textureCoordinates));
// look up the color of the texture image specified by
// the uniform "_MainTex" at the position specified by
// "textureCoordinates.x" and "textureCoordinates.y"
// and return it in "gl_FragColor"
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Unlit/Texture"
}
Note that the name _MainTex was chosen to make sure that the fallback shader Unlit/Texture can access it (see the discussion of fallback shaders in Section “Diffuse Reflection”).
The sphere should now be white. If it is grey, you should check whether the shader is attached to the material and the material is attached to the sphere. If the sphere is magenta, you should check the shader code. In particular, you should select the shader in the Project View and read the error message in the Inspector View.
If the sphere is white, select the sphere in the Hierarchy View or the Scene View and look at the information in the Inspector View. Your material should appear under Mesh Renderer and under it should be a label Texture Image. (Otherwise click on the material bar to make it appear.) The label “Texture Image” is the same that we specified for our shader property _MainTex in the shader code. There is an empty box to the right of this label. Either click on the small Select button in the box and select the imported texture image or drag & drop the texture image from the Project View to this empty box.
If everything went right, the texture image should now appear on the sphere. Congratulations!
How It Works
[edit | edit source]Since many techniques use texture mapping, it pays off very well to understand what is happening here. Therefore, let's review the shader code:
The vertices of Unity's sphere object come with attribute data in gl_MultiTexCoord0 for each vertex, which specifies texture coordinates that are similar to longitude and latitude (but range from 0 to 1). This is analogous to the attribute gl_Vertex, which specifies a position in object space, except that gl_MultiTexCoord0 specifies texture coordinates in the space of the texture image.
The vertex shader then writes the texture coordinates of each vertex to the varying variable textureCoordinates. For each fragment of a triangle (i.e. each covered pixel), the values of this varying at the three triangle vertices are interpolated (see the description in Section “Rasterization”) and the interpolated texture coordinates are given to the fragment shader. The fragment shader then uses them to look up a color in the texture image specified by the uniform _MainTex at the interpolated position in texture space and returns this color in gl_FragColor, which is then written to the framebuffer and displayed on the screen.
It is crucial that you gain a good idea of these steps in order to understand the more complicated texture mapping techniques presented in other tutorials.
Repeating and Moving Textures
[edit | edit source]In Unity's interface for the shader above, you might have noticed the parameters Tiling and Offset, each with an x and a y component. In built-in shaders, these parameters allow you to repeat the texture (by shrinking the texture image in texture coordinate space) and move the texture image on the surface (by offsetting it in texture coordinate space). In order to be consistent with this behavior, another uniform has to be defined:
uniform vec4 _MainTex_ST;
// tiling and offset parameters of property "_MainTex"
For each texture property, Unity offers such a vec4 uniform with the ending “_ST”. (Remember: “S” and “T” are the official names of the texture coordinates, which are usually called “U” and “V”, or “x” and “y”.) This uniform holds the x and y components of the Tiling parameter in _MainTex_ST.x and _MainTex_ST.y, while the x and y components of the Offset parameter are stored in _MainTex_ST.w and _MainTex_ST.z. The uniform should be used like this:
gl_FragColor = texture2D(_MainTex,
_MainTex_ST.xy * textureCoordinates.xy
+ _MainTex_ST.zw);
This makes the shader behave like the built-in shaders. In the other tutorials, this feature is usually not implemented in order to keep the shader code a bit cleaner.
And just for completeness, here is the complete shader code with this feature:
Shader "GLSL shader with single texture" {
Properties {
_MainTex ("Texture Image", 2D) = "white" {}
}
SubShader {
Pass {
GLSLPROGRAM
uniform sampler2D _MainTex;
uniform vec4 _MainTex_ST;
// tiling and offset parameters of property
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = texture2D(_MainTex,
_MainTex_ST.xy * textureCoordinates.xy
+ _MainTex_ST.zw);
// textureCoordinates are multiplied with the tiling
// parameters and the offset parameters are added
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Unlit/Texture"
}
Summary
[edit | edit source]You have reached the end of one of the most important tutorials. We have looked at:
- How to import a texture image and how to attach it to a texture property of a shader.
- How a vertex shader and a fragment shader work together to map a texture image onto a mesh.
- How Unity's tiling and offset parameters for textures work and how to implement them.
Further Reading
[edit | edit source]If you want to know more
- about the data flow in and out of vertex shaders and fragment shaders (i.e. vertex attributes, varyings, etc.), you should read the description in Section “OpenGL ES 2.0 Pipeline”.
- about the interpolation of varying variables for the fragment shader, you should read the discussion in Section “Rasterization”.
Lighting Textured Surfaces
[edit | edit source]
This tutorial covers per-vertex lighting of textured surfaces.
It combines the shader code of Section “Textured Spheres” and Section “Specular Highlights” to compute lighting with a diffuse material color determined by a texture. If you haven't read those sections, this would be a very good opportunity to read them.
Texturing and Diffuse Per-Vertex Lighting
[edit | edit source]In Section “Textured Spheres”, the texture color was used as output of the fragment shader. However, it is also possible to use the texture color as any of the parameters in lighting computations, in particular the material constant for diffuse reflection, which was introduced in Section “Diffuse Reflection”. It appears in the diffuse part of the Phong reflection model:
where this equation is used with different material constants for the three color components red, green, and blue. By using a texture to determine these material constants, they can vary over the surface.
Shader Code
[edit | edit source]In comparison to the per-vertex lighting in Section “Specular Highlights”, the vertex shader here computes two varying colors: diffuseColor is multiplied with the texture color in the fragment shader and specularColor is just the specular term, which shouldn't be multiplied with the texture color. This makes perfect sense but for historically reasons (i.e. older graphics hardware that was less capable) this is sometimes referred to as “separate specular color”; in fact, Unity's ShaderLab has an option called “SeparateSpecular” to activate or deactivate it.
Note that a property _Color is included, which is multiplied (component-wise) to all parts of the diffuseColor; thus, it acts as a useful color filter to tint or shade the texture color. Moreover, a property with this name is required to make the fallback shader work (see also the discussion of fallback shaders in Section “Diffuse Reflection”).
Shader "GLSL per-vertex lighting with texture" {
Properties {
_MainTex ("Texture For Diffuse Material Color", 2D) = "white" {}
_Color ("Overall Diffuse Color Filter", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform sampler2D _MainTex;
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec3 diffuseColor;
// diffuse Phong lighting computed in the vertex shader
varying vec3 specularColor;
// specular Phong lighting computed in the vertex shader
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 viewDirection = normalize(vec3(
vec4(_WorldSpaceCameraPos, 1.0)
- modelMatrix * gl_Vertex));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource = vec3(_WorldSpaceLightPos0
- modelMatrix * gl_Vertex);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
diffuseColor = ambientLighting + diffuseReflection;
specularColor = specularReflection;
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(diffuseColor
* vec3(texture2D(_MainTex, vec2(textureCoordinates)))
+ specularColor, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform sampler2D _MainTex;
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec3 diffuseColor;
// diffuse Phong lighting computed in the vertex shader
varying vec3 specularColor;
// specular Phong lighting computed in the vertex shader
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 viewDirection = normalize(vec3(
vec4(_WorldSpaceCameraPos, 1.0)
- modelMatrix * gl_Vertex));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource = vec3(_WorldSpaceLightPos0
- modelMatrix * gl_Vertex);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
diffuseColor = diffuseReflection;
specularColor = specularReflection;
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(diffuseColor
* vec3(texture2D(_MainTex, vec2(textureCoordinates)))
+ specularColor, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
In order to assign a texture image to this shader, you should follow the steps discussed in Section “Textured Spheres”.
Summary
[edit | edit source]Congratulations, you have reached the end. We have looked at:
- How texturing and per-vertex lighting are usually combined.
- What a “separate specular color” is.
Further Reading
[edit | edit source]If you still want to know more
- about fallback shaders or the diffuse reflection term of the Phong reflection model, you should read Section “Diffuse Reflection”.
- about per-vertex lighting or the rest of the Phong reflection model, i.e. the ambient and the specular term, you should read Section “Specular Highlights”.
- about the basics of texturing, you should read Section “Textured Spheres”.
Glossy Textures
[edit | edit source]
This tutorial covers per-pixel lighting of partially glossy, textured surfaces.
It combines the shader code of Section “Textured Spheres” and Section “Smooth Specular Highlights” to compute per-pixel lighting with a material color for diffuse reflection that is determined by the RGB components of a texture and an intensity of the specular reflection that is determined by the A component of the same texture. If you haven't read those sections, this would be a very good opportunity to read them.
Gloss Mapping
[edit | edit source]In Section “Lighting Textured Surfaces”, the material constant for the diffuse reflection was determined by the RGB components of a texture image. Here we extend this technique and determine the strength of the specular reflection by the A (alpha) component of the same texture image. Using only one texture offers a significant performance advantage, in particular because an RGBA texture lookup is under certain circumstances just as expensive as an RGB texture lookup.
If the “gloss” of a texture image (i.e. the strength of the specular reflection) is encoded in the A (alpha) component of an RGBA texture image, we can simply multiply the material constant for the specular reflection with the alpha component of the texture image. was introduced in Section “Specular Highlights” and appears in the specular reflection term of the Phong reflection model:
If multiplied with the alpha component of the texture image, this term reaches its maximum (i.e. the surface is glossy) where alpha is 1, and it is 0 (i.e. the surface is not glossy at all) where alpha is 0.

Shader Code for Per-Pixel Lighting
[edit | edit source]The shader code is a combination of the per-pixel lighting from Section “Smooth Specular Highlights” and the texturing from Section “Textured Spheres”. Similarly to Section “Lighting Textured Surfaces”, the RGB components of the texture color in textureColor is multiplied to the diffuse material color _Color.
In the particular texture image to the left, the alpha component is 0 for water and 1 for land. However, it should be the water that is glossy and the land that isn't. Thus, with this particular image, we should multiply the specular material color with (1.0 - textureColor.a). On the other hand, usual gloss maps would require a multiplication with textureColor.a. (Note how easy it is to make this kind of changes to a shader program.)
Shader "GLSL per-pixel lighting with texture" {
Properties {
_MainTex ("RGBA Texture For Material Color", 2D) = "white" {}
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform sampler2D _MainTex;
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
textureCoordinates = gl_MultiTexCoord0;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
vec4 textureColor =
texture2D(_MainTex, vec2(textureCoordinates));
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting = vec3(gl_LightModel.ambient)
* vec3(_Color) * vec3(textureColor);
vec3 diffuseReflection = attenuation * vec3(_LightColor0)
* vec3(_Color) * vec3(textureColor)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * (1.0 - textureColor.a)
// for usual gloss maps: "... * textureColor.a"
* pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(ambientLighting
+ diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform sampler2D _MainTex;
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
textureCoordinates = gl_MultiTexCoord0;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
vec4 textureColor =
texture2D(_MainTex, vec2(textureCoordinates));
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection = attenuation * vec3(_LightColor0)
* vec3(_Color) * vec3(textureColor)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * (1.0 - textureColor.a)
// for usual gloss maps: "... * textureColor.a"
* pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor =
vec4(diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
A useful modification of this shader for the particular texture image above, would be to set the diffuse material color to a dark blue where the alpha component is 0.
Shader Code for Per-Vertex Lighting
[edit | edit source]As discussed in Section “Smooth Specular Highlights”, specular highlights are usually not rendered very well with per-vertex lighting. Sometimes, however, there is no choice because of performance limitations. In order to include gloss mapping in the shader code of Section “Lighting Textured Surfaces”, the fragment shaders of both passes should be replaced with this code:
#ifdef FRAGMENT
void main()
{
vec4 textureColor =
texture2D(_MainTex, vec2(textureCoordinates));
gl_FragColor = vec4(diffuseColor * vec3(textureColor)
+ specularColor * (1.0 - textureColor.a), 1.0);
}
#endif
Note that a usual gloss map would require a multiplication with textureColor.a instead of (1.0 - textureColor.a).
Summary
[edit | edit source]Congratulations! You finished an important tutorial about gloss mapping. We have looked at:
- What gloss mapping is.
- How to implement it for per-pixel lighting.
- How to implement it for per-vertex lighting.
Further Reading
[edit | edit source]If you still want to learn more
- about per-pixel lighting (without texturing), you should read Section “Smooth Specular Highlights”.
- about texturing, you should read Section “Textured Spheres”.
- about per-vertex lighting with texturing, you should read Section “Lighting Textured Surfaces”.
Transparent Textures
[edit | edit source]
This tutorial covers various common uses of alpha texture maps, i.e. RGBA texture images with an A (alpha) component that specifies the opacity of texels.
It combines the shader code of Section “Textured Spheres” with concepts that were introduced in Section “Cutaways” and Section “Transparency”.
If you haven't read these tutorials, this would be a very good opportunity to read them.
Discarding Transparent Fragments
[edit | edit source]Let's start with discarding fragments as explained in Section “Cutaways”. Follow the steps described in Section “Textured Spheres” and assign the image to the left to the material of a sphere with the following shader:
Shader "GLSL texturing with alpha discard" {
Properties {
_MainTex ("RGBA Texture Image", 2D) = "white" {}
_Cutoff ("Alpha Cutoff", Float) = 0.5
}
SubShader {
Pass {
Cull Off // since the front is partially transparent,
// we shouldn't cull the back
GLSLPROGRAM
uniform sampler2D _MainTex;
uniform float _Cutoff;
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor =
texture2D(_MainTex, vec2(textureCoordinates));
if (gl_FragColor.a < _Cutoff)
// alpha value less than user-specified threshold?
{
discard; // yes: discard this fragment
}
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Unlit/Transparent Cutout"
}
The fragment shader reads the RGBA texture and compares the alpha value against a user-specified threshold. If the alpha value is less than the threshold, the fragment is discarded and the surface appears transparent.
Alpha Testing
[edit | edit source]The same effect as described above can be implemented with an alpha test. The advantage of the alpha test is that it runs also on older hardware that doesn't support GLSL. Here is the code, which results in more or less the same result as the shader above:
Shader "GLSL texturing with alpha test" {
Properties {
_MainTex ("RGBA Texture Image", 2D) = "white" {}
_Cutoff ("Alpha Cutoff", Float) = 0.5
}
SubShader {
Pass {
Cull Off // since the front is partially transparent,
// we shouldn't cull the back
AlphaTest Greater [_Cutoff] // specify alpha test:
// fragment passes if alpha is greater than _Cutoff
GLSLPROGRAM
uniform sampler2D _MainTex;
uniform float _Cutoff;
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor =
texture2D(_MainTex, vec2(textureCoordinates));
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Unlit/Transparent Cutout"
}
Here, no explicit discard instruction is necessary but the alpha test has to be configured to pass only those fragments with an alpha value of more than the _Cutoff property; otherwise they are discarded. More details about the alpha test are available in Unity's ShaderLab documentation.
Note that the alpha test and the discard instruction are rather slow on some platforms, in particular on mobile devices. Thus, blending is often a more efficient alternative.
Blending
[edit | edit source]The Section “Transparency” described how to render semitransparent objects with alpha blending. Combining this with an RGBA texture results in this code:
Shader "GLSL texturing with alpha blending" {
Properties {
_MainTex ("RGBA Texture Image", 2D) = "white" {}
}
SubShader {
Tags {"Queue" = "Transparent"}
Pass {
Cull Front // first render the back faces
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend SrcAlpha OneMinusSrcAlpha
// blend based on the fragment's alpha value
GLSLPROGRAM
uniform sampler2D _MainTex;
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor =
texture2D(_MainTex, vec2(textureCoordinates));
}
#endif
ENDGLSL
}
Pass {
Cull Back // now render the front faces
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend SrcAlpha OneMinusSrcAlpha
// blend based on the fragment's alpha value
GLSLPROGRAM
uniform sampler2D _MainTex;
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor =
texture2D(_MainTex, vec2(textureCoordinates));
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Unlit/Transparent"
}
Note that all texels with an alpha value of 0 are black in this particular texture image. In fact, the colors in this texture image are “premultiplied” with their alpha value. (Such colors are also called “opacity-weighted.”) Thus, for this particular image, we should actually specify the blend equation for premultiplied colors in order to avoid another multiplication of the colors with their alpha value in the blend equation. Therefore, an improvement of the shader (for this particular texture image) is to employ the following blend specification in both passes:
Blend One OneMinusSrcAlpha

Blending with Customized Colors
[edit | edit source]We should not end this tutorial without a somewhat more practical application of the presented techniques. To the left is an image of a globe with semitransparent blue oceans, which I found on Wikimedia Commons. There is some lighting (or silhouette enhancement) going on, which I didn't try to reproduce. Instead, I only tried to reproduce the basic idea of semitransparent oceans with the following shader, which ignores the RGB colors of the texture map and replaces them by specific colors based on the alpha value:
Shader "GLSL semitransparent colors based on alpha" {
Properties {
_MainTex ("RGBA Texture Image", 2D) = "white" {}
}
SubShader {
Tags {"Queue" = "Transparent"}
Pass {
Cull Front // first render the back faces
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend SrcAlpha OneMinusSrcAlpha
// blend based on the fragment's alpha value
GLSLPROGRAM
uniform sampler2D _MainTex;
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor =
texture2D(_MainTex, vec2(textureCoordinates));
if (gl_FragColor.a > 0.5) // opaque back face?
{
gl_FragColor = vec4(0.0, 0.0, 0.2, 1.0);
// opaque dark blue
}
else // transparent back face?
{
gl_FragColor = vec4(0.0, 0.0, 1.0, 0.3);
// semitransparent dark blue
}
}
#endif
ENDGLSL
}
Pass {
Cull Back // now render the front faces
ZWrite Off // don't write to depth buffer
// in order not to occlude other objects
Blend SrcAlpha OneMinusSrcAlpha
// blend based on the fragment's alpha value
GLSLPROGRAM
uniform sampler2D _MainTex;
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor =
texture2D(_MainTex, vec2(textureCoordinates));
if (gl_FragColor.a > 0.5) // opaque front face?
{
gl_FragColor = vec4(0.0, 1.0, 0.0, 1.0);
// opaque green
}
else // transparent front face
{
gl_FragColor = vec4(0.0, 0.0, 1.0, 0.3);
// semitransparent dark blue
}
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Unlit/Transparent"
}
Of course, it would be interesting to add lighting and silhouette enhancement to this shader. One could also change the opaque, green color in order to take the texture color into account, e.g. with:
gl_FragColor = vec4(0.5 * gl_FragColor.r, 2.0 * gl_FragColor.g, 0.5 * gl_FragColor.b, 1.0);
which emphasizes the green component by multiplying it with 2 and dims the red and blue components by multiplying them with 0.5. However, this results in oversaturated green that is clamped to the maximum intensity. This can be avoided by halving the difference of the green component to the maximum intensity 1. This difference is 1.0 - gl_FragColor.g; half of it is 0.5 * (1.0 - gl_FragColor.g) and the value corresponding to this reduced distance to the maximum intensity is: 1.0 - 0.5 * (1.0 - gl_FragColor.g). Thus, in order to avoid oversaturation of green, we could use (instead of the opaque green color):
gl_FragColor = vec4(0.5 * gl_FragColor.r, 1.0 - 0.5 * (1.0 - gl_FragColor.g), 0.5 * gl_FragColor.b, 1.0);
In practice, one has to try various possibilities for such color transformations. To this end, the use of numeric shader properties (e.g. for the factors 0.5 in the line above) is particularly useful to interactively explore the possibilities.
Summary
[edit | edit source]Congratulations! You have reached the end of this rather long tutorial. We have looked at:
- How discarding fragments can be combined with alpha texture maps.
- How the alpha test can be used to achieve the same effect.
- How alpha texture maps can be used for blending.
- How alpha texture maps can be used to determine colors.
Further Reading
[edit | edit source]If you still want to know more
- about texturing, you should read Section “Textured Spheres”.
- about discarding fragments, you should read Section “Cutaways”.
- about the alpha test, you should read Unity's ShaderLab documentation: Alpha testing.
- about blending, you should read Section “Transparency”.
Layers of Textures
[edit | edit source]
This tutorial introduces multitexturing, i.e. the use of multiple texture images in a shader.
It extends the shader code of Section “Textured Spheres” to multiple textures and shows a way of combining them. If you haven't read that tutorial, this would be a very good opportunity to read it.
Layers of Surfaces
[edit | edit source]Many real surfaces (e.g. the human skin illustrated in the image to the left) consist of several layers of different colors, transparencies, reflectivities, etc. If the topmost layer is opaque and doesn't transmit any light, this doesn't really matter for rendering the surface. However, in many cases the topmost layer is (semi)transparent and therefore an accurate rendering of the surface has to take multiple layers into account.
In fact, the specular reflection that is included in the Phong reflection model (see Section “Specular Highlights”) often corresponds to a transparent layer that reflects light: sweat on human skin, wax on fruits, transparent plastics with embedded pigment particles, etc. On the other hand, the diffuse reflection corresponds to the layer(s) below the topmost transparent layer.
Lighting such layered surfaces doesn't require a geometric model of the layers: they can be represented by a single, infinitely thin polygon mesh. However, the lighting computation has to compute different reflections for different layers and has to take the transmission of light between layers into account (both when light enters the layer and when it exits the layer). Examples of this approach are included in the “Dawn” demo by Nvidia (see Chapter 3 of the book “GPU Gems”, which is available online) and the “Human Head” demo by Nvidia (see Chapter 14 of the book “GPU Gems 3”, which is also available online).
A full description of these processes is beyond the scope of this tutorial. Suffice to say that layers are often associated with texture images to specify their characteristics. Here we just show how to use two textures and one particular way of combining them. The example is in fact not related to layers and therefore illustrates that multitexturing has more applications than layers of surfaces.

Lit and Unlit Earth
[edit | edit source]Due to human activities, the unlit side of the Earth is not completely dark. Instead, artificial lights mark the position and extension of cities as shown in the image to the left. Therefore, diffuse lighting of the Earth should not just dim the texture image for the sunlit surface but actually blend it to the unlit texture image. Note that the sunlit Earth is far brighter than human-made lights on the unlit side; however, we reduce this contrast in order to show off the nighttime texture.
The shader code extends the code from Section “Textured Spheres” to two texture images and uses the computation described in Section “Diffuse Reflection” for a single, directional light source:
According to this equation, the level of diffuse lighting levelOfLighting is max(0, N·L). We then blend the colors of the daytime texture and the nighttime texture based on levelOfLighting. This could be achieved by multiplying the daytime color with levelOfLighting and multiplying the nighttime color with 1.0 - levelOfLighting before adding them to determine the fragment's color. Alternatively, the built-in GLSL function mix can be used (mix(a, b, w) = b*w + a*(1.0-w)), which is likely to be more efficient. Thus, the fragment shader could be:
#ifdef FRAGMENT
void main()
{
vec4 nighttimeColor = _Color
* texture2D(_MainTex, vec2(textureCoordinates));
vec4 daytimeColor = _LightColor0
* texture2D(_DecalTex, vec2(textureCoordinates));
gl_FragColor =
mix(nighttimeColor, daytimeColor, levelOfLighting);
// = daytimeColor * levelOfLighting
// + nighttimeColor * (1.0 - levelOfLighting)
}
#endif
Note that this blending is very similar to the alpha blending that was discussed in Section “Transparency” except that we perform the blending inside a fragment shader and use levelOfLighting instead of the alpha component (i.e. the opacity) of the texture that should be blended “over” the other texture. In fact, if _DecalTex specified an alpha component (see Section “Transparent Textures”), we could use this alpha component to blend _DecalTex over _MainTex. This is actually what Unity's standard Decal shader does and it corresponds to a layer which is partially transparent on top of an opaque layer that is visible where the topmost layer is transparent.
Complete Shader Code
[edit | edit source]The names of the properties of the shader were chosen to agree with the property names of the fallback shader — in this case the Decal shader (note that the fallback Decal shade and the standard Decal shader appear to use the two textures in opposite ways). Also, an additional property _Color is introduced and multiplied (component-wise) to the texture color of the nighttime texture in order to control its overall brightness. Furthermore, the color of the light source _LightColor0 is multiplied (also component-wise) to the color of the daytime texture in order to take colored light sources into account.
Shader "GLSL multitexturing of Earth" {
Properties {
_DecalTex ("Daytime Earth", 2D) = "white" {}
_MainTex ("Nighttime Earth", 2D) = "white" {}
_Color ("Nighttime Color Filter", Color) = (1,1,1,1)
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for the first, directional light
GLSLPROGRAM
uniform sampler2D _MainTex;
uniform sampler2D _DecalTex;
uniform vec4 _Color;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying float levelOfLighting;
// level of diffuse lighting computed in vertex shader
varying vec4 textureCoordinates;
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 lightDirection;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
lightDirection = vec3(0.0, 0.0, 0.0);
// ignore other light sources
}
levelOfLighting =
max(0.0, dot(normalDirection, lightDirection));
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec4 nighttimeColor = _Color
* texture2D(_MainTex, vec2(textureCoordinates));
vec4 daytimeColor = _LightColor0
* texture2D(_DecalTex, vec2(textureCoordinates));
gl_FragColor =
mix(nighttimeColor, daytimeColor, levelOfLighting);
// = daytimeColor * levelOfLighting
// + nighttimeColor * (1.0 - levelOfLighting)
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Decal"
}
When you run this shader, make sure that you have an activated directional light source in your scene.
Summary
[edit | edit source]Congratulations! You have reached the end of the last tutorial on basic texturing. We have looked at:
- How layers of surfaces can influence the appearance of materials (e.g. human skin, waxed fruits, plastics, etc.)
- How artificial lights on the unlit side can be taken into account when texturing a sphere representing the Earth.
- How to implement this technique in a shader.
- How this is related to blending an alpha texture over a second opaque texture.
Further Reading
[edit | edit source]If you still want to know more
- about basic texturing, you should read Section “Textured Spheres”.
- about diffuse reflection, you should read Section “Diffuse Reflection”.
- about alpha textures, you should read Section “Transparent Textures”.
- about advanced skin rendering, you could read Chapter 3 “Skin in the ‘Dawn’ Demo” by Curtis Beeson and Kevin Bjorke of the book “GPU Gems” by Randima Fernando (editor) published 2004 by Addison-Wesley, which is available online, and Chapter 14 “Advanced Techniques for Realistic Real-Time Skin Rendering” by Eugene d’Eon and David Luebke of the book “GPU Gems 3” by Hubert Nguyen (editor) published 2007 by Addison-Wesley, which is also available online.
Lighting of Bumpy Surfaces
[edit | edit source]
This tutorial covers normal mapping.
It's the first in a series of tutorials about texturing techniques that go beyond two-dimensional surfaces (or layers of surfaces). In this tutorial, we start with normal mapping, which is a very well established technique to fake the lighting of small bumps and dents — even on coarse polygon meshes. The code of this tutorial is based on Section “Smooth Specular Highlights” and Section “Textured Spheres”.
Perceiving Shapes Based on Lighting
[edit | edit source]The painting by Caravaggio depicted to the left is about the incredulity of Saint Thomas, who did not believe in Christ's resurrection until he put his finger in Christ's side. The furrowed brows of the apostles not only symbolize this incredulity but clearly convey it by means of a common facial expression. However, why do we know that their foreheads are actually furrowed instead of being painted with some light and dark lines? After all, this is just a flat painting. In fact, viewers intuitively make the assumption that these are furrowed instead of painted brows — even though the painting itself allows for both interpretations. The lesson is: bumps on smooth surfaces can often be convincingly conveyed by the lighting alone without any other cues (shadows, occlusions, parallax effects, stereo, etc.).
Normal Mapping
[edit | edit source]Normal mapping tries to convey bumps on smooth surfaces (i.e. coarse triangle meshes with interpolated normals) by changing the surface normal vectors according to some virtual bumps. When the lighting is computed with these modified normal vectors, viewers will often perceive the virtual bumps — even though a perfectly flat triangle has been rendered. The illusion can certainly break down (in particular at silhouettes) but in many cases it is very convincing.
More specifically, the normal vectors that represent the virtual bumps are first encoded in a texture image (i.e. a normal map). A fragment shader then looks up these vectors in the texture image and computes the lighting based on them. That's about it. The problem, of course, is the encoding of the normal vectors in a texture image. There are different possibilities and the fragment shader has to be adapted to the specific encoding that was used to generate the normal map.

Normal Mapping in Unity
[edit | edit source]The very good news is that you can easily create normal maps from gray-scale images with Unity: create a gray-scale image in your favorite paint program and use a specific gray for the regular height of the surface, lighter grays for bumps, and darker grays for dents. Make sure that the transitions between different grays are smooth, e.g. by blurring the image. When you import the image with Assets > Import New Asset change the Texture Type in the Inspector View to Normal map and check Generate from greyscale. After clicking Apply, the preview should show a bluish image with reddish and greenish edges. Alternatively to generating a normal map, the encoded normal map to the left can be imported (don't forget to uncheck the Generate from greyscale box).
The not so good news is that the fragment shader has to do some computations to decode the normals. First of all, the texture color is stored in a two-component texture image, i.e. there is only an alpha component and one color component available. The color component can be accessed as the red, green, or blue component — in all cases the same value is returned. Here, we use the green component since Unity also uses it. The two components, and , are stored as numbers between 0 and 1; however, they represent coordinates and between -1 and 1. The mapping is:
and
From these two components, the third component of the three-dimensional normal vector n can be calculated because of the normalization to unit length:
Only the “+” solution is necessary if we choose the axis along the axis of the smooth normal vector (interpolated from the normal vectors that were set in the vertex shader) since we aren't able to render surfaces with an inwards pointing normal vector anyways. The code snippet from the fragment shader could look like this:
vec4 encodedNormal = texture2D(_BumpMap,
_BumpMap_ST.xy * textureCoordinates.xy
+ _BumpMap_ST.zw);
vec3 localCoords =
vec3(2.0 * encodedNormal.ag - vec2(1.0), 0.0);
localCoords.z = sqrt(1.0 - dot(localCoords, localCoords));
// approximation without sqrt: localCoords.z =
// 1.0 - 0.5 * dot(localCoords, localCoords);
The decoding for devices that use OpenGL ES is actually simpler since Unity doesn't use a two-component texture in this case. Thus, for mobile platforms the decoding becomes:
vec4 encodedNormal = texture2D(_BumpMap,
_BumpMap_ST.xy * textureCoordinates.xy
+ _BumpMap_ST.zw);
vec3 localCoords = 2.0 * encodedNormal.rgb - vec3(1.0);
However, the rest of this tutorial (and also Section “Projection of Bumpy Surfaces”) will cover only (desktop) OpenGL.

Unity uses a local surface coordinate systems for each point of the surface to specify normal vectors in the normal map. The axis of this local coordinates system is given by the smooth, interpolated normal vector N in world space and the plane is a tangent plane to the surface as illustrated in the image to the left. Specifically, the axis is specified by the tangent attribute T that Unity provides to vertices (see the discussion of attributes in Section “Debugging of Shaders”). Given the and axis, the axis can be computed by a cross product in the vertex shader, e.g. B = N × T. (The letter B refers to the traditional name “binormal” for this vector.)
Note that the normal vector N is transformed with the transpose of the inverse model matrix from object space to world space (because it is orthogonal to a surface; see Section “Applying Matrix Transformations”) while the tangent vector T specifies a direction between points on a surface and is therefore transformed with the model matrix. The binormal vector B represents a third class of vectors which are transformed differently. (If you really want to know: the skew-symmetric matrix B corresponding to “B×” is transformed like a quadratic form.) Thus, the best choice is to first transform N and T to world space, and then to compute B in world space using the cross product of the transformed vectors.
With the normalized directions T, B, and N in world space, we can easily form a matrix that maps any normal vector n of the normal map from the local surface coordinate system to world space because the columns of such a matrix are just the vectors of the axes; thus, the 3×3 matrix for the mapping of n to world space is:
These calculations are performed by the vertex shader, for example this way:
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec4 textureCoordinates;
varying mat3 localSurface2World; // mapping from
// local surface coordinates to world coordinates
#ifdef VERTEX
attribute vec4 Tangent;
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
localSurface2World[0] = normalize(vec3(
modelMatrix * vec4(vec3(Tangent), 0.0)));
localSurface2World[2] = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
localSurface2World[1] = normalize(
cross(localSurface2World[2], localSurface2World[0])
* Tangent.w); // factor Tangent.w is specific to Unity
position = modelMatrix * gl_Vertex;
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
The factor Tangent.w in the computation of binormal is specific to Unity, i.e. Unity provides tangent vectors and normal maps such that we have to do this multiplication.
In the fragment shader, we multiply the matrix in localSurface2World with n. For example, with this line:
vec3 normalDirection =
normalize(localSurface2World * localCoords);
With the new normal vector in world space, we can compute the lighting as in Section “Smooth Specular Highlights”.
Complete Shader Code
[edit | edit source]This shader code simply integrates all the snippets and uses our standard two-pass approach for pixel lights.
Shader "GLSL normal mapping" {
Properties {
_BumpMap ("Normal Map", 2D) = "bump" {}
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform sampler2D _BumpMap;
uniform vec4 _BumpMap_ST;
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec4 textureCoordinates;
varying mat3 localSurface2World; // mapping from local
// surface coordinates to world coordinates
#ifdef VERTEX
attribute vec4 Tangent;
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
localSurface2World[0] = normalize(vec3(
modelMatrix * vec4(vec3(Tangent), 0.0)));
localSurface2World[2] = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
localSurface2World[1] = normalize(
cross(localSurface2World[2], localSurface2World[0])
* Tangent.w); // factor Tangent.w is specific to Unity
position = modelMatrix * gl_Vertex;
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
// in principle we have to normalize the columns of
// "localSurface2World" again; however, the potential
// problems are small since we use this matrix only to
// compute "normalDirection", which we normalize anyways
vec4 encodedNormal = texture2D(_BumpMap,
_BumpMap_ST.xy * textureCoordinates.xy
+ _BumpMap_ST.zw);
vec3 localCoords =
vec3(2.0 * encodedNormal.ag - vec2(1.0), 0.0);
localCoords.z = sqrt(1.0 - dot(localCoords, localCoords));
// approximation without sqrt: localCoords.z =
// 1.0 - 0.5 * dot(localCoords, localCoords);
vec3 normalDirection =
normalize(localSurface2World * localCoords);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(ambientLighting
+ diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform sampler2D _BumpMap;
uniform vec4 _BumpMap_ST;
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec4 textureCoordinates;
varying mat3 localSurface2World; // mapping from
// local surface coordinates to world coordinates
#ifdef VERTEX
attribute vec4 Tangent;
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
localSurface2World[0] = normalize(vec3(
modelMatrix * vec4(vec3(Tangent), 0.0)));
localSurface2World[2] = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
localSurface2World[1] = normalize(
cross(localSurface2World[2], localSurface2World[0])
* Tangent.w); // factor Tangent.w is specific to Unity
position = modelMatrix * gl_Vertex;
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
// in principle we have to normalize the columns of
// "localSurface2World" again; however, the potential
// problems are small since we use this matrix only to
// compute "normalDirection", which we normalize anyways
vec4 encodedNormal = texture2D(_BumpMap,
_BumpMap_ST.xy * textureCoordinates.xy
+ _BumpMap_ST.zw);
vec3 localCoords =
vec3(2.0 * encodedNormal.ag - vec2(1.0), 0.0);
localCoords.z = sqrt(1.0 - dot(localCoords, localCoords));
// approximation without sqrt: localCoords.z =
// 1.0 - 0.5 * dot(localCoords, localCoords);
vec3 normalDirection =
normalize(localSurface2World * localCoords);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor =
vec4(diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Bumped Specular"
}
Note that we have used the tiling and offset uniform _BumpMap_ST as explained in the Section “Textured Spheres” since this option is often particularly useful for bump maps.
Summary
[edit | edit source]Congratulations! You finished this tutorial! We have look at:
- How human perception of shapes often relies on lighting.
- What normal mapping is.
- How Unity encodes normal maps.
- How a fragment shader can decode Unity's normal maps and use them to per-pixel lighting.
Further Reading
[edit | edit source]If you still want to know more
- about texture mapping (including tiling and offseting), you should read Section “Textured Spheres”.
- about per-pixel lighting with the Phong reflection model, you should read Section “Smooth Specular Highlights”.
- about transforming normal vectors, you should read Section “Applying Matrix Transformations”.
- about normal mapping, you could read Mark J. Kilgard: “A Practical and Robust Bump-mapping Technique for Today’s GPUs”, GDC 2000: Advanced OpenGL Game Development, which is available online.
Projection of Bumpy Surfaces
[edit | edit source]
This tutorial covers (single-step) parallax mapping.
It extends and is based on Section “Lighting of Bumpy Surfaces”.
Improving Normal Mapping
[edit | edit source]The normal mapping technique presented in Section “Lighting of Bumpy Surfaces” only changes the lighting of a flat surface to create the illusion of bumps and dents. If one looks straight onto a surface (i.e. in the direction of the surface normal vector), this works very well. However, if one looks onto a surface from some other angle (as in the image to the left), the bumps should also stick out of the surface while the dents should recede into the surface. Of course, this could be achieved by geometrically modeling bumps and dents; however, this would require to process many more vertices. On the other hand, single-step parallax mapping is a very efficient techniques similar to normal mapping, which doesn't require additional triangles but can still move virtual bumps by several pixels to make them stick out of a flat surface. However, the technique is limited to bumps and dents of small heights and requires some fine-tuning for best results.

Parallax Mapping Explained
[edit | edit source]Parallax mapping was proposed in 2001 by Tomomichi Kaneko et al. in their paper “Detailed shape representation with parallax mapping” (ICAT 2001). The basic idea is to offset the texture coordinates that are used for the texturing of the surface (in particular normal mapping). If this offset of texture coordinates is computed appropriately, it is possible to move parts of the texture (e.g. bumps) as if they were sticking out of the surface.
The illustration to the left shows the view vector V in the direction to the viewer and the surface normal vector N in the point of a surface that is rasterized in a fragment shader. Parallax mapping proceeds in 3 steps:
- Lookup of the height at the rasterized point in a height map, which is depicted by the wavy line on top of the straight line at the bottom in the illustration.
- Computation of the intersection of the viewing ray in direction of V with a surface at height parallel to the rendered surface. The distance is the distance between the rasterized surface point moved by in the direction of N and this intersection point. If these two points are projected onto the rendered surface, is also the distance between the rasterized point and a new point on the surface (marked by a cross in the illustration). This new surface point is a better approximation to the point that is actually visible for the view ray in direction V if the surface was displaced by the height map.
- Transformation of the offset into texture coordinate space in order to compute an offset of texture coordinates for all following texture lookups.
For the computation of we require the height of a height map at the rasterized point, which is implemented in the example by a texture lookup in the A component of the texture property _ParallaxMap, which should be a gray-scale image representing heights as discussed in Section “Lighting of Bumpy Surfaces”. We also require the view direction V in the local surface coordinate system formed by the normal vector ( axis), the tangent vector ( axis), and the binormal vector ( axis), which was also introduced Section “Lighting of Bumpy Surfaces”. To this end we compute a transformation from local surface coordinates to object space with:
where T, B and N are given in object coordinates. (In Section “Lighting of Bumpy Surfaces” we had a similar matrix but with vectors in world coordinates.)
We compute the view direction V in object space (as the difference between the rasterized position and the camera position transformed from world space to object space) and then we transform it to the local surface space with the matrix which can be computed as:
This is possible because T, B and N are orthogonal and normalized. (Actually, the situation is a bit more complicated because we won't normalize these vectors but use their length for another transformation; see below.) Thus, in order to transform V from object space to the local surface space, we have to multiply it with the transposed matrix . In GLSL, this is achieved by multiplying the vector from the left to the matrix .
Once we have the V in the local surface coordinate system with the axis in the direction of the normal vector N, we can compute the offsets (in direction) and (in direction) by using similar triangles (compare with the illustration):
and .
Thus:
and .
Note that it is not necessary to normalize V because we use only ratios of its components, which are not affected by the normalization.
Finally, we have to transform and into texture space. This would be quite difficult if Unity wouldn't help us: the tangent attribute Tangent is actually appropriately scaled and has a fourth component Tangent.w for scaling the binormal vector such that the transformation of the view direction V scales and appropriately to have and in texture coordinate space without further computations.
Implementation
[edit | edit source]The implementation shares most of the code with Section “Lighting of Bumpy Surfaces”. In particular, the same scaling of the binormal vector with the fourth component of the Tangent attribute is used in order to take the mapping of the offsets from local surface space to texture space into account:
vec3 binormal = cross(gl_Normal, vec3(Tangent)) * Tangent.w;
In the vertex shader, we have to add a varying for the view vector V in the local surface coordinate system (with the scaling of axes to take the mapping to texture space into account). This varying is called viewDirInScaledSurfaceCoords. It is computed by multiplying the view vector in object coordinates (viewDirInObjectCoords) from the left to the matrix (localSurface2ScaledObject) as explained above:
vec3 viewDirInObjectCoords = vec3(
modelMatrixInverse * vec4(_WorldSpaceCameraPos, 1.0)
- gl_Vertex);
mat3 localSurface2ScaledObject =
mat3(vec3(Tangent), binormal, gl_Normal);
// vectors are orthogonal
viewDirInScaledSurfaceCoords =
viewDirInObjectCoords * localSurface2ScaledObject;
// we multiply with the transpose to multiply with
// the "inverse" (apart from the scaling)
The rest of the vertex shader is the same as for normal mapping, see Section “Lighting of Bumpy Surfaces”.
In the fragment shader, we first query the height map for the height of the rasterized point. This height is specified by the A component of the texture _ParallaxMap. The values between 0 and 1 are transformed to the range -_Parallax/2 to +_Parallax with a shader property _Parallax in order to offer some user control over the strength of the effect (and to be compatible with the fallback shader):
float height = _Parallax
* (-0.5 + texture2D(_ParallaxMap, _ParallaxMap_ST.xy
* textureCoordinates.xy + _ParallaxMap_ST.zw).a);
The offsets and are then computed as described above. However, we also clamp each offset between a user-specified interval -_MaxTexCoordOffset and _MaxTexCoordOffset in order to make sure that the offset stays in reasonable bounds. (If the height map consists of more or less flat plateaus of constant height with smooth transitions between these plateaus, _MaxTexCoordOffset should be smaller than the thickness of these transition regions; otherwise the sample point might be in a different plateau with a different height, which would mean that the approximation of the intersection point is arbitrarily bad.) The code is:
vec2 texCoordOffsets =
clamp(height * viewDirInScaledSurfaceCoords.xy
/ viewDirInScaledSurfaceCoords.z,
-_MaxTexCoordOffset, +_MaxTexCoordOffset);
In the following code, we have to apply the offsets to the texture coordinates in all texture lookups; i.e., we have to replace vec2(textureCoordinates) (or equivalently textureCoordinates.xy) by (textureCoordinates.xy + texCoordOffsets), e.g.:
vec4 encodedNormal = texture2D(_BumpMap,
_BumpMap_ST.xy * (textureCoordinates.xy
+ texCoordOffsets) + _BumpMap_ST.zw);
The rest of the fragment shader code is just as it was for Section “Lighting of Bumpy Surfaces”.
Complete Shader Code
[edit | edit source]As discussed in the previous section, most of this code is taken from Section “Lighting of Bumpy Surfaces”. Note that if you want to use the code on a mobile device with OpenGL ES, make sure to change the decoding of the normal map as described in that tutorial.
The part about parallax mapping is actually only a few lines. Most of the names of the shader properties were chosen according to the fallback shader; the user interface labels are much more descriptive.
Shader "GLSL parallax mapping" {
Properties {
_BumpMap ("Normal Map", 2D) = "bump" {}
_ParallaxMap ("Heightmap (in A)", 2D) = "black" {}
_Parallax ("Max Height", Float) = 0.01
_MaxTexCoordOffset ("Max Texture Coordinate Offset", Float) =
0.01
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform sampler2D _BumpMap;
uniform vec4 _BumpMap_ST;
uniform sampler2D _ParallaxMap;
uniform vec4 _ParallaxMap_ST;
uniform float _Parallax;
uniform float _MaxTexCoordOffset;
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 unity_Scale; // w = 1/uniform scale;
// should be multiplied to _World2Object
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec4 textureCoordinates;
varying mat3 localSurface2World; // mapping from
// local surface coordinates to world coordinates
varying vec3 viewDirInScaledSurfaceCoords;
#ifdef VERTEX
attribute vec4 Tangent;
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object * unity_Scale.w;
localSurface2World[0] = normalize(vec3(
modelMatrix * vec4(vec3(Tangent), 0.0)));
localSurface2World[2] = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
localSurface2World[1] = normalize(
cross(localSurface2World[2], localSurface2World[0])
* Tangent.w);
vec3 binormal =
cross(gl_Normal, vec3(Tangent)) * Tangent.w;
// appropriately scaled tangent and binormal
// to map distances from object space to texture space
vec3 viewDirInObjectCoords = vec3(modelMatrixInverse
* vec4(_WorldSpaceCameraPos, 1.0) - gl_Vertex);
mat3 localSurface2ScaledObject =
mat3(vec3(Tangent), binormal, gl_Normal);
// vectors are orthogonal
viewDirInScaledSurfaceCoords =
viewDirInObjectCoords * localSurface2ScaledObject;
// we multiply with the transpose to multiply
// with the "inverse" (apart from the scaling)
position = modelMatrix * gl_Vertex;
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
// parallax mapping: compute height and
// find offset in texture coordinates
// for the intersection of the view ray
// with the surface at this height
float height =
_Parallax * (-0.5 + texture2D(_ParallaxMap,
_ParallaxMap_ST.xy * textureCoordinates.xy
+ _ParallaxMap_ST.zw).a);
vec2 texCoordOffsets =
clamp(height * viewDirInScaledSurfaceCoords.xy
/ viewDirInScaledSurfaceCoords.z,
-_MaxTexCoordOffset, +_MaxTexCoordOffset);
// normal mapping: lookup and decode normal from bump map
// in principle we have to normalize the columns
// of "localSurface2World" again; however, the potential
// problems are small since we use this matrix only
// to compute "normalDirection", which we normalize anyways
vec4 encodedNormal = texture2D(_BumpMap,
_BumpMap_ST.xy * (textureCoordinates.xy
+ texCoordOffsets) + _BumpMap_ST.zw);
vec3 localCoords =
vec3(2.0 * encodedNormal.ag - vec2(1.0), 0.0);
localCoords.z = sqrt(1.0 - dot(localCoords, localCoords));
// approximation without sqrt: localCoords.z =
// 1.0 - 0.5 * dot(localCoords, localCoords);
vec3 normalDirection =
normalize(localSurface2World * localCoords);
// per-pixel lighting using the Phong reflection model
// (with linear attenuation for point and spot lights)
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(ambientLighting + diffuseReflection
+ specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform sampler2D _BumpMap;
uniform vec4 _BumpMap_ST;
uniform sampler2D _ParallaxMap;
uniform vec4 _ParallaxMap_ST;
uniform float _Parallax;
uniform float _MaxTexCoordOffset;
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 unity_Scale; // w = 1/uniform scale;
// should be multiplied to _World2Object
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec4 textureCoordinates;
varying mat3 localSurface2World; // mapping
// from local surface coordinates to world coordinates
varying vec3 viewDirInScaledSurfaceCoords;
#ifdef VERTEX
attribute vec4 Tangent;
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object * unity_Scale.w;
localSurface2World[0] = normalize(vec3(
modelMatrix * vec4(vec3(Tangent), 0.0)));
localSurface2World[2] = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
localSurface2World[1] = normalize(
cross(localSurface2World[2], localSurface2World[0])
* Tangent.w);
vec3 binormal =
cross(gl_Normal, vec3(Tangent)) * Tangent.w;
// appropriately scaled tangent and binormal
// to map distances from object space to texture space
vec3 viewDirInObjectCoords = vec3(modelMatrixInverse
* vec4(_WorldSpaceCameraPos, 1.0) - gl_Vertex);
mat3 localSurface2ScaledObject =
mat3(vec3(Tangent), binormal, gl_Normal);
// vectors are orthogonal
viewDirInScaledSurfaceCoords =
viewDirInObjectCoords * localSurface2ScaledObject;
// we multiply with the transpose to multiply
// with the "inverse" (apart from the scaling)
position = modelMatrix * gl_Vertex;
textureCoordinates = gl_MultiTexCoord0;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
// parallax mapping: compute height and
// find offset in texture coordinates
// for the intersection of the view ray
// with the surface at this height
float height =
_Parallax * (-0.5 + texture2D(_ParallaxMap,
_ParallaxMap_ST.xy * textureCoordinates.xy
+ _ParallaxMap_ST.zw).a);
vec2 texCoordOffsets =
clamp(height * viewDirInScaledSurfaceCoords.xy
/ viewDirInScaledSurfaceCoords.z,
-_MaxTexCoordOffset, +_MaxTexCoordOffset);
// normal mapping: lookup and decode normal from bump map
// in principle we have to normalize the columns
// of "localSurface2World" again; however, the potential
// problems are small since we use this matrix only to
// compute "normalDirection", which we normalize anyways
vec4 encodedNormal = texture2D(_BumpMap,
_BumpMap_ST.xy * (textureCoordinates.xy
+ texCoordOffsets) + _BumpMap_ST.zw);
vec3 localCoords =
vec3(2.0 * encodedNormal.ag - vec2(1.0), 0.0);
localCoords.z = sqrt(1.0 - dot(localCoords, localCoords));
// approximation without sqrt: localCoords.z =
// 1.0 - 0.5 * dot(localCoords, localCoords);
vec3 normalDirection =
normalize(localSurface2World * localCoords);
// per-pixel lighting using the Phong reflection model
// (with linear attenuation for point and spot lights)
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor =
vec4(diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Parallax Specular"
}
Summary
[edit | edit source]Congratulations! If you actually understand the whole shader, you have come a long way. In fact, the shader includes lots of concepts (transformations between coordinate systems, application of the inverse of an orthogonal matrix by multiplying a vector from the left to it, the Phong reflection model, normal mapping, parallax mapping, ...). More specifically, we have seen:
- How parallax mapping improves upon normal mapping.
- How parallax mapping is described mathematically.
- How parallax mapping is implemented.
Further Reading
[edit | edit source]If you still want to know more
- about details of the shader code, you should read Section “Lighting of Bumpy Surfaces”.
- about parallax mapping, you could read the original publication by Tomomichi Kaneko et al.: “Detailed shape representation with parallax mapping”, ICAT 2001, pages 205–208, which is available online.
Cookies
[edit | edit source]

This tutorial covers projective texture mapping in light space, which is useful to implement cookies for spotlights and directional light sources. (In fact, Unity uses a built-in cookie for any spotlight.)
The tutorial is based on the code of Section “Smooth Specular Highlights” and Section “Transparent Textures”. If you haven't read those tutorials yet, you should read them first.
Gobos and Cookies in Real Life
[edit | edit source]In real life, gobos are pieces of material (often metal) with holes that are placed in front of light sources to manipulate the shape of light beams or shadows. Cookies (or “cuculoris”) serve a similar purpose but are placed at a larger distance from the light source as shown in the image to the left.
Unity's Cookies
[edit | edit source]In Unity, a cookie can be specified for each light source in the Inspector View when the light source is selected. This cookie is basically an alpha texture map (see Section “Transparent Textures”) that is placed in front of the light source and moves with it (therefore it is actually similar to a gobo). It lets light pass through where the alpha component of the texture image is 1 and blocks light where the alpha component is 0. Unity's cookies for spotlights and directional lights are just square, two-dimensional alpha texture maps. On the other hand, cookies for point lights are cube maps, which we will not cover here.
In order to implement a cookie, we have to extend the shader of any surface that should be affected by the cookie. (This is very different from how Unity's projectors work; see Section “Projectors”.) Specifically, we have to attenuate the light of each light source according to its cookie in the lighting computation of a shader. Here, we use the per-pixel lighting described in Section “Smooth Specular Highlights”; however, the technique can be applied to any lighting computation.
In order to find the relevant position in the cookie texture, the position of the rasterized point of a surface is transformed into the coordinate system of the light source. This coordinate system is very similar to the clip coordinate system of a camera, which is described in Section “Vertex Transformations”. In fact, the best way to think of the coordinate system of a light source is probably to think of the light source as a camera. The x and y light coordinates are then related to the screen coordinates of this hypothetical camera. Transforming a point from world coordinates to light coordinates is actually very easy because Unity provides the required 4×4 matrix as the uniform variable _LightMatrix0. (Otherwise we would have to set up the matrix similar to the matrices for the viewing transformation and the projection, which are discussed in Section “Vertex Transformations”.)
For best efficiency, the transformation of the surface point from world space to light space should be performed by multiplying _LightMatrix0 to the position in world space in the vertex shader, for example this way:
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from Lighting.cginc)
uniform mat4 _LightMatrix0; // transformation
// from world to light space (from Autolight.cginc)
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec4 positionInLightSpace;
// position of the vertex (and fragment) in light space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
positionInLightSpace = _LightMatrix0 * position;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
Apart from the definitions of the uniform _LightMatrix0 and the varying positionInLightSpace and the instruction to compute positionInLightSpace, this is the same vertex shader as in Section “Smooth Specular Highlights”.
Cookies for Directional Light Sources
[edit | edit source]For the cookie of a directional light source, we can just use the x and y light coordinates in positionInLightSpace as texture coordinates for a lookup in the cookie texture _LightTexture0. This texture lookup should be performed in the fragment shader. Then the resulting alpha component should be multiplied to the computed lighting; for example:
// compute diffuseReflection and specularReflection
float cookieAttenuation = 1.0;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
cookieAttenuation = texture2D(_LightTexture0,
vec2(positionInLightSpace)).a;
}
// compute cookieAttenuation for spotlights here
gl_FragColor = vec4(cookieAttenuation
* (diffuseReflection + specularReflection), 1.0);
Instead of vec2(positionInLightSpace) we could also use positionInLightSpace.xy to get a two-dimensional vector with the x and y coordinates in light space.
Cookies for Spotlights
[edit | edit source]For spotlights, the x and y light coordinates in positionInLightSpace have to be divided by the w light coordinate. This division is characteristic for projective texture mapping and corresponds to the perspective division for a camera, which is described in Section “Vertex Transformations”. Unity defines the matrix _LightMatrix0 such that we have to add to both coordinates after the division:
cookieAttenuation = texture2D(_LightTexture0,
vec2(positionInLightSpace) / positionInLightSpace.w
+ vec2(0.5)).a;
For some GPUs it might be more efficient to use the built-in function texture2DProj, which takes three texture coordinates in a vec3 and divides the first two coordinates by the third coordinate before the texture lookup. A problem with this approach is that we have to add after the division by positionInLightSpace.w; however, texture2DProj doesn't allow us to add anything after the internal division by the third texture coordinate. The solution is to add 0.5 * positionInLightSpace.w before the division by positionInLightSpace.w, which corresponds to adding after the division:
vec3 textureCoords = vec3(vec2(positionInLightSpace)
+ vec2(0.5 * positionInLightSpace.w),
positionInLightSpace.w);
cookieAttenuation =
texture2DProj(_LightTexture0, textureCoords).a;
Note that the texture lookup for directional lights can also be implemented with texture2DProj by setting textureCoords to vec3(vec2(positionInLightSpace), 1.0). This would allow us to use only one texture lookup for both directional lights and for spotlights, which is more efficient on some GPUs.
Complete Shader Code
[edit | edit source]For the complete shader code we use a simplified version of the ForwardBase pass of Section “Smooth Specular Highlights” since Unity only uses a directional light without cookie in the ForwardBase pass. All light sources with cookies are handled by the ForwardAdd pass. We ignore cookies for point lights, for which _LightMatrix0[3][3] is 1.0 (but we include them in the next section). Spotlights always have a cookie texture: if the user didn't specify one, Unity supplies a cookie texture to generate the shape of a spotlight; thus, it is OK to always apply the cookie. Directional lights don't always have a cookie; however, if there is only one directional light source without cookie then it has been processed in the ForwardBase pass. Thus, unless there are more than one directional light sources without cookies, we can assume that all directional light sources in the ForwardAdd pass have cookies. In this case, the complete shader code could be:
Shader "GLSL per-pixel lighting with cookies" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" } // pass for ambient light
// and first directional light source without cookie
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from Lighting.cginc)
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection =
normalize(vec3(_WorldSpaceLightPos0));
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection = vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(ambientLighting
+ diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from Lighting.cginc)
uniform mat4 _LightMatrix0; // transformation
// from world to light space (from Autolight.cginc)
uniform sampler2D _LightTexture0;
// cookie alpha texture map (from Autolight.cginc)
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec4 positionInLightSpace;
// position of the vertex (and fragment) in light space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
positionInLightSpace = _LightMatrix0 * position;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
float cookieAttenuation = 1.0;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
cookieAttenuation = texture2D(_LightTexture0,
vec2(positionInLightSpace)).a;
}
else if (1.0 != _LightMatrix0[3][3])
// spotlight (i.e. not a point light)?
{
cookieAttenuation = texture2D(_LightTexture0,
vec2(positionInLightSpace) / positionInLightSpace.w
+ vec2(0.5)).a;
}
gl_FragColor = vec4(cookieAttenuation
* (diffuseReflection + specularReflection), 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Shader Programs for Specific Light Sources
[edit | edit source]The previous shader code is limited to scenes with at most one directional light source without a cookie. Also, it doesn't take cookies of point light sources into account. Writing more general shader code requires different ForwardAdd passes for different light sources. (Remember that the light source in the ForwardBase pass is always a directional light source without cookie.) Fortunately, Unity offers a way to generate multiple shaders by using the following Unity-specific directive (right after GLSLPROGRAM in the ForwardAdd pass):
#pragma multi_compile_lightpass
With this instruction, Unity will compile the shader code for the ForwardAdd pass multiple times for different kinds of light sources. Each compilation is distinguished by the definition of one of the following symbols: DIRECTIONAL, DIRECTIONAL_COOKIE, POINT, POINT_NOATT, POINT_COOKIE, SPOT. The shader code should check which symbol is defined (using the directives #if defined ... #elif defined ... #endif) and include appropriate instructions. For example:
Shader "GLSL per-pixel lighting with cookies" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" } // pass for ambient light
// and first directional light source without cookie
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from Lighting.cginc)
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection =
normalize(vec3(_WorldSpaceLightPos0));
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection = vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(ambientLighting
+ diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
#pragma multi_compile_lightpass
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from Lighting.cginc)
uniform mat4 _LightMatrix0; // transformation
// from world to light space (from Autolight.cginc)
#if defined DIRECTIONAL_COOKIE || defined SPOT
uniform sampler2D _LightTexture0;
// cookie alpha texture map (from Autolight.cginc)
#elif defined POINT_COOKIE
uniform samplerCube _LightTexture0;
// cookie alpha texture map (from Autolight.cginc)
#endif
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec4 positionInLightSpace;
// position of the vertex (and fragment) in light space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
positionInLightSpace = _LightMatrix0 * position;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation = 1.0;
// by default no attenuation with distance
#if defined DIRECTIONAL || defined DIRECTIONAL_COOKIE
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
#elif defined POINT_NOATT
lightDirection =
normalize(vec3(_WorldSpaceLightPos0 - position));
#elif defined POINT || defined POINT_COOKIE || defined SPOT
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
#endif
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
float cookieAttenuation = 1.0;
// by default no cookie attenuation
#if defined DIRECTIONAL_COOKIE
cookieAttenuation = texture2D(_LightTexture0,
vec2(positionInLightSpace)).a;
#elif defined POINT_COOKIE
cookieAttenuation = textureCube(_LightTexture0,
vec3(positionInLightSpace)).a;
#elif defined SPOT
cookieAttenuation = texture2D(_LightTexture0,
vec2(positionInLightSpace)
/ positionInLightSpace.w + vec2(0.5)).a;
#endif
gl_FragColor = vec4(cookieAttenuation *
(diffuseReflection + specularReflection), 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Note that the cookie for a point light source is using a cube texture map. This kind of texture map is discussed in Section “Reflecting Surfaces”.
Summary
[edit | edit source]Congratulations, you have learned the most important aspects of projective texture mapping. We have seen:
- How to implement cookies for directional light sources.
- How to implement spotlights (with and without user-specified cookies).
- How to implement different shaders for different light sources.
Further Reading
[edit | edit source]If you still want to know more
- about the shader version for lights without cookies, you should read Section “Smooth Specular Highlights”.
- about texture mapping and in particular alpha texture maps, you should read Section “Transparent Textures”.
- about projective texture mapping in fixed-function OpenGL, you could read NVIDIA's white paper “Projective Texture Mapping” by Cass Everitt (which is available online).
Light Attenuation
[edit | edit source]
This tutorial covers textures for light attenuation or — more generally spoken — textures as lookup tables.
It is based on Section “Cookies”. If you haven't read that tutorial yet, you should read it first.
Texture Maps as Lookup Tables
[edit | edit source]One can think of a texture map as an approximation to a two-dimensional function that maps the texture coordinates to an RGBA color. If one of the two texture coordinates is kept fixed, the texture map can also represent a one-dimensional function. Thus, it is often possible to replace mathematical expressions that depend only on one or two variables by lookup tables in the form of texture maps. (The limitation is that the resolution of the texture map is limited by the size of the texture image and therefore the accuracy of a texture lookup might be insufficient.)
The main advantage of using such a texture lookup is a potential gain of performance: a texture lookup doesn't depend on the complexity of the mathematical expression but only on the size of the texture image (to a certain degree: the smaller the texture image the more efficient the caching up to the point where the whole texture fits into the cache). However, there is an overhead of using a texture lookup; thus, replacing simple mathematical expressions — including built-in functions — is usually pointless.
Which mathematical expressions should be replaced by texture lookups? Unfortunately, there is no general answer because it depends on the specific GPU whether a specific lookup is faster than evaluating a specific mathematical expression. However, one should keep in mind that a texture map is less simple (since it requires code to compute the lookup table), less explicit (since the mathematical function is encoded in a lookup table), less consistent with other mathematical expressions, and has a wider scope (since the texture is available in the whole fragment shader). These are good reasons to avoid lookup tables. However, the gains in performance might outweigh these reasons. In that case, it is a good idea to include comments that document how to achieve the same effect without the lookup table.
Unity's Texture Lookup for Light Attenuation
[edit | edit source]Unity actually uses a lookup texture _LightTextureB0 internally for the light attenuation of point lights and spotlights. (Note that in some cases, e.g. point lights without cookie textures, this lookup texture is set to _LightTexture0 without B. This case is ignored here.) In Section “Diffuse Reflection”, it was described how to implement linear attenuation: we compute an attenuation factor that includes one over the distance between the position of the light source in world space and the position of the rendered fragment in world space. In order to represent this distance, Unity uses the coordinate in light space. Light space coordinates have been discussed in Section “Cookies”; here, it is only important that we can use the Unity-specific uniform matrix _LightMatrix0 to transform a position from world space to light space. Analogously to the code in Section “Cookies”, we store the position in light space in the varying variable positionInLightSpace. We can then use the coordinate of this varying to look up the attenuation factor in the alpha component of the texture _LightTextureB0 in the fragment shader:
float distance = positionInLightSpace.z;
// use z coordinate in light space as signed distance
attenuation =
texture2D(_LightTextureB0, vec2(distance)).a;
// texture lookup for attenuation
// alternative with linear attenuation:
// float distance = length(vertexToLightSource);
// attenuation = 1.0 / distance;
Using the texture lookup, we don't have to compute the length of a vector (which involves three squares and one square root) and we don't have to divide by this length. In fact, the actual attenuation function that is implemented in the lookup table is more complicated in order to avoid saturated colors at short distances. Thus, compared to a computation of this actual attenuation function, we save even more operations.
Complete Shader Code
[edit | edit source]The shader code is based on the code of Section “Cookies”. The ForwardBase pass was slightly simplified by assuming that the light source is always directional without attenuation. The vertex shader of the ForwardAdd pass is identical to the code in Section “Cookies” but the fragment shader includes the texture lookup for light attenuation, which is described above. However, the fragment shader lacks the cookie attenuation in order to focus on the attenuation with distance. It is straightforward (and a good exercise) to include the code for the cookie again.
Shader "GLSL light attenuation with texture lookup" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and
// first directional light source without attenuation
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from Lighting.cginc)
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection =
normalize(vec3(_WorldSpaceLightPos0));
// we assume that the light source in ForwardBase pass
// is a directional light source without attenuation
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection = vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(ambientLighting
+ diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from Lighting.cginc)
uniform mat4 _LightMatrix0; // transformation
// from world to light space (from Autolight.cginc)
uniform sampler2D _LightTextureB0;
// texture lookup (from Autolight.cginc)
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec4 positionInLightSpace;
// position of the vertex (and fragment) in light space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
positionInLightSpace = _LightMatrix0 * position;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
lightDirection = normalize(vertexToLightSource);
float distance = positionInLightSpace.z;
// use z coordinate in light space as signed distance
attenuation =
texture2D(_LightTextureB0, vec2(distance)).a;
// texture lookup for attenuation
// alternative with linear attenuation:
// float distance = length(vertexToLightSource);
// attenuation = 1.0 / distance;
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor =
vec4(diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
If you compare the lighting computed by this shader with the lighting of a built-in shader, you will notice a difference in intensity by a factor of about 2 to 4. However, this is mainly due to additional constant factors in the built-in shaders. It is straightforward to introduce similar constant factors in the code above.
It should be noted that the coordinate in light space is not equal to the distance from the light source; it's not even proportional to that distance. In fact, the meaning of the coordinate depends on the matrix _LightMatrix0, which is an undocumented feature of Unity and can therefore change anytime. However, it is rather safe to assume that a value of 0 corresponds to very close positions and a value of 1 corresponds to farther positions.
Also note that point lights without cookie textures specify the attenuation lookup texture in _LightTexture0 instead of _LightTextureB0; thus, the code above doesn't work for them. Moreover, the code doesn't check the sign of the coordinate, which is fine for spot lights but results in a lack of attenuation on one side of point light sources.
Computing Lookup Textures
[edit | edit source]So far, we have used a lookup texture that is provided by Unity. If Unity wouldn't provide us with the texture in _LightTextureB0, we had to compute this texture ourselves. Here is some JavaScript code to compute a similar lookup texture. In order to use it, you have to change the name _LightTextureB0 to _LookupTexture in the shader code and attach the following JavaScript to any game object with the corresponding material:
@script ExecuteInEditMode()
public var upToDate : boolean = false;
function Start()
{
upToDate = false;
}
function Update()
{
if (!upToDate) // is lookup texture not up to date?
{
upToDate = true;
var texture = new Texture2D(16, 16);
// width = 16 texels, height = 16 texels
texture.filterMode = FilterMode.Bilinear;
texture.wrapMode = TextureWrapMode.Clamp;
renderer.sharedMaterial.SetTexture("_LookupTexture", texture);
// "_LookupTexture" has to correspond to the name
// of the uniform sampler2D variable in the shader
for (var j : int = 0; j < texture.height; j++)
{
for (var i : int = 0; i < texture.width; i++)
{
var x : float = (i + 0.5) / texture.width;
// first texture coordinate
var y : float = (j + 0.5) / texture.height;
// second texture coordinate
var color = Color(0.0, 0.0, 0.0, (1.0 - x) * (1.0 - x));
// set RGBA of texels
texture.SetPixel(i, j, color);
}
}
texture.Apply(); // apply all the texture.SetPixel(...) commands
}
}
In this code, i and j enumerate the texels of the texture image while x and y represent the corresponding texture coordinates. The function (1.0-x)*(1.0-x) for the alpha component of the texture image happens to produce similar results as compared to Unity's lookup texture.
Note that the lookup texture should not be computed in every frame. Rather it should be computed only when necessary. If a lookup texture depends on additional parameters, then the texture should only be recomputed if any parameter has been changed. This can be achieved by storing the parameter values for which a lookup texture has been computed and continuously checking whether any of the new parameters are different from these stored values. If this is the case, the lookup texture has to be recomputed.
Summary
[edit | edit source]Congratulations, you have reached the end of this tutorial. We have seen:
- How to use the built-in texture
_LightTextureB0as a lookup table for light attenuation. - How to compute your own lookup textures in JavaScript.
Further Reading
[edit | edit source]If you still want to know more
- about light attenuation for light sources, you should read Section “Diffuse Reflection”.
- about basic texture mapping, you should read Section “Textured Spheres”.
- about coordinates in light space, you should read Section “Cookies”.
- about the SECS principles (simple, explicit, consistent, minimal scope), you could read Chapter 3 of David Straker's book “C Style: Standards and Guidelines”, published by Prentice-Hall in 1991, which is available online.
Projectors
[edit | edit source]
This tutorial covers projective texture mapping for projectors, which are particular rendering components of Unity.
It is based on Section “Cookies”. If you haven't read that tutorial yet, you should read it first.
Unity's Projectors
[edit | edit source]Unity's projectors are somewhat similar to spotlights. In fact, they can be used for similar applications. There is, however, an important technical difference: For spotlights, the shaders of all lit objects have to compute the lighting by the spotlight as discussed in Section “Cookies”. If the shader of an object ignores the spotlight, it just won't be lit by the spotlight. This is different for projectors: Each projector is associated with a material with a shader that is applied to any object in the projector's range. Thus, an object's shader doesn't need to deal with the projector; instead, the projector applies its shader to all objects in its range as an additional render pass in order to achieve certain effects, e.g. adding the light of a projected image or attenuating the color of an object to fake a shadow. In fact, various effects can be achieved by using different blend equations of the projector's shader. (Blend equations are discussed in Section “Transparency”.)
One might even consider projectors as the more “natural” way of implementing lights. However, the interaction between light and materials is usually specific to each material while the single shader of a projector cannot deal with all these differences. This limits the possibilities of projectors to three basic behaviors: adding light to an object, modulating an object's color, or both, adding light and modulating the object's color. We will look at adding light to an object and attenuating an object's colors as an example of modulating them.
Projectors for Adding Light
[edit | edit source]In order to create a projector, choose GameObject > Create Empty from the main menu and then (with the new object still selected) Component > Effects > Projector from the main menu. You have now a projector that can be manipulated similarly to a spotlight. The settings of the projector in the Inspector View are discussed in Unity's reference manual. Here, the only important setting is the projector's Material, which will be applied to all objects in its range. Thus, we have to create another material and assign a suitable shader to it. This shader usually doesn't have access to the materials of the game objects, which it is applied to; therefore, it doesn't have access to their textures etc. Neither does it have access to any information about light sources. However, it has access to the attributes of the vertices of the game objects and its own shader properties.
A shader to add light to objects could be used to project any image onto other objects, similarly to an overhead projector or a movie projector. Thus, it should use a texture image similar to a cookie for spotlights (see Section “Cookies”) except that the RGB colors of the texture image should be added to allow for colored projections. We achieve this by setting the fragment color to the RGBA color of the texture image and using the blend equation
Blend One One
which just adds the fragment color to the color in the framebuffer. (Depending on the texture image, it might be better to use Blend SrcAlpha One in order to remove any colors with zero opacity.)
Another difference to the cookies of spotlights is that we should use the Unity-specific uniform matrix _Projector to transform positions from object space to projector space instead of the matrix _LightMatrix0. However, coordinates in projector space work very similar to coordinates in light space — except that the resulting and coordinates are in the correct range; thus, we don't have to bother with adding 0.5. Nonetheless, we have to perform the division by the coordinates (as always for projective texture mapping); either by explicitly dividing and by or by using texture2DProj:
Shader "GLSL projector shader for adding light" {
Properties {
_ShadowTex ("Projected Image", 2D) = "white" {}
}
SubShader {
Pass {
Blend One One
// add color of _ShadowTex to the color in the framebuffer
GLSLPROGRAM
// User-specified properties
uniform sampler2D _ShadowTex;
// Projector-specific uniforms
uniform mat4 _Projector; // transformation matrix
// from object space to projector space
varying vec4 positionInProjSpace;
// position of the vertex (and fragment) in projector space
#ifdef VERTEX
void main()
{
positionInProjSpace = _Projector * gl_Vertex;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
if (positionInProjSpace.w > 0.0) // in front of projector?
{
gl_FragColor = texture2D(_ShadowTex ,
vec2(positionInProjSpace) / positionInProjSpace.w);
// alternatively: gl_FragColor = texture2DProj(
// _ShadowTex, vec3(positionInProjSpace));
}
else // behind projector
{
gl_FragColor = vec4(0.0);
}
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Projector/Light"
}
Notice that we have to test whether is positive (i.e. the fragment is in front of the projector, not behind it). Without this test, the projector would also add light to objects behind it. Furthermore, the texture image has to be square and it is usually a good idea to use textures with wrap mode set to clamp.
Just in case you wondered: the shader property for the texture is called _ShadowTex in order to be compatible with the built-in shaders for projectors.

Projectors for Modulating Colors
[edit | edit source]The basic steps of creating a projector for modulating colors are the same as above. The only difference is the shader code. The following example adds a drop shadow by attenuating colors, in particular the floor's color. Note that in an actual application, the color of the shadow caster should not be attenuated. This can be achieved by assigning the shadow caster to a particular Layer (in the Inspector View of the game object) and specifying this layer under Ignore Layers in the Inspector View of the projector.
In order to give the shadow a certain shape, we use the alpha component of a texture image to determine how dark the shadow is. (Thus, we can use the cookie textures for lights in the standard assets.) In order to attenuate the color in the framebuffer, we should multiply it with 1 minus alpha (i.e. factor 0 for alpha equals 1). Therefore, the appropriate blend equation is:
Blend Zero OneMinusSrcAlpha
The Zero indicates that we don't add any light. Even if the shadow is too dark, no light should be added; instead, the alpha component should be reduced in the fragment shader, e.g. by multiplying it with a factor less than 1. For an independent modulation of the color components in the framebuffer, we would require Blend Zero SrcColor or Blend Zero OneMinusSrcColor.
The different blend equation is actually about the only change in the shader code compared to the version for adding light:
Shader "GLSL projector shader for drop shadows" {
Properties {
_ShadowTex ("Shadow Shape", 2D) = "white" {}
}
SubShader {
Pass {
Blend Zero OneMinusSrcAlpha // attenuate color in framebuffer
// by 1 minus alpha of _ShadowTex
GLSLPROGRAM
// User-specified properties
uniform sampler2D _ShadowTex;
// Projector-specific uniforms
uniform mat4 _Projector; // transformation matrix
// from object space to projector space
varying vec4 positionInProjSpace;
// position of the vertex (and fragment) in projector space
#ifdef VERTEX
void main()
{
positionInProjSpace = _Projector * gl_Vertex;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
if (positionInProjSpace.w > 0.0) // in front of projector?
{
gl_FragColor = texture2D(_ShadowTex ,
vec2(positionInProjSpace) / positionInProjSpace.w);
// alternatively: gl_FragColor = texture2DProj(
// _ShadowTex, vec3(positionInProjSpace));
}
else // behind projector
{
gl_FragColor = vec4(0.0);
}
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Projector/Light"
}
Summary
[edit | edit source]Congratulations, this is the end of this tutorial. We have seen:
- How Unity's projectors work.
- How to implement a shader for a projector to add light to objects.
- How to implement a shader for a projector to attenuate objects' colors.
Further Reading
[edit | edit source]If you still want to know more
- about the light space (which is very similar to projector space), you should read Section “Cookies”.
- about texture mapping and in particular alpha texture maps, you should read Section “Transparent Textures”.
- about projective texture mapping in fixed-function OpenGL, you could read NVIDIA's white paper “Projective Texture Mapping” by Cass Everitt (which is available online).
- about Unity's projectors, you should read Unity's documentation about projectors.
Reflecting Surfaces
[edit | edit source]This tutorial introduces reflection mapping (and cube maps to implement it).
It's the first in a small series of tutorials about environment mapping using cube maps in Unity. The tutorial is based on the per-pixel lighting described in Section “Smooth Specular Highlights” and on the concept of texture mapping, which was introduced in Section “Textured Spheres”.
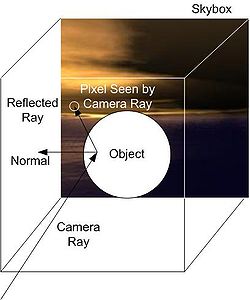
Reflection Mapping with a Skybox
[edit | edit source]The illustration to the left depicts the concept of reflection mapping with a static skybox: a view ray is reflected at a point on the surface of an object and the reflected ray is intersected with the skybox to determine the color of the corresponding pixel. The skybox is just a large cube with textured faces surrounding the whole scene. It should be noted that skyboxes are usually static and don't include any dynamic objects of the scene. However, “skyboxes” for reflection mapping are often rendered to include the scene from a certain point of view. This is, however, beyond the scope of this tutorial.
Moreover, this tutorial covers only the computation of the reflection, it doesn't cover the rendering of the skybox, which is discussed in Section “Skyboxes”. For the reflection of a skybox in an object, we have to render the object and reflect the rays from the camera to the surface points at the surface normal vectors. The mathematics of this reflection is the same as for the reflection of a light ray at a surface normal vector, which was discussed in Section “Specular Highlights”.
Once we have the reflected ray, its intersection with a large skybox has to be computed. This computation actually becomes easier if the skybox is infinitely large: in that case the position of the surface point doesn't matter at all since its distance from the origin of the coordinate system is infinitely small compared to the size of the skybox; thus, only the direction of the reflected ray matters but not its position. Therefore, we can actually also think of a ray that starts in the center of a small skybox instead of a ray that starts somewhere in an infinitely large skybox. (If you are not familiar with this idea, you probably need a bit of time to accept it.) Depending on the direction of the reflected ray, it will intersect one of the six faces of the textured skybox. We could compute, which face is intersected and where the face is intersected and then do a texture lookup (see Section “Textured Spheres”) in the texture image for the specific face. However, GLSL offers cube maps, which support exactly this kind of texture lookups in the six faces of a cube using a direction vector. Thus, all we need to do, is to provide a cube map for the environment as a shader property and use the textureCube instruction with the reflected direction to get the color at the corresponding position in the cube map.
Cube Maps
[edit | edit source]A cube map shader property called _Cube can be defined this way in a Unity shader:
Properties {
_Cube ("Reflection Map", Cube) = "" {}
}
The corresponding uniform variable is defined this way in a GLSL shader:
uniform samplerCube _Cube;
To create a cube map, select Create > Cubemap in the Project View. Then you have to specify six texture images for the faces of the cube in the Inspector View. Examples for such textures can be found in Standard Assets > Skyboxes > Textures. Furthermore, you should check MipMaps in the Inspector View for the cube map; this should produce considerably better visual results for reflection mapping.
The vertex shader has to compute the view direction viewDirection and the normal direction normalDirection as discussed in Section “Specular Highlights”. To reflect the view direction in the fragment shader, we can use the GLSL function reflect as also discussed in Section “Specular Highlights”:
vec3 reflectedDirection =
reflect(viewDirection, normalize(normalDirection));
And to perform the texture lookup in the cube map and store the resulting color in the fragment color, we simply use:
gl_FragColor = textureCube(_Cube, reflectedDirection);
That's about it.
Complete Shader Code
[edit | edit source]The shader code then becomes:
Shader "GLSL shader with reflection map" {
Properties {
_Cube("Reflection Map", Cube) = "" {}
}
SubShader {
Pass {
GLSLPROGRAM
// User-specified uniforms
uniform samplerCube _Cube;
// The following built-in uniforms
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
// Varyings
varying vec3 normalDirection;
varying vec3 viewDirection;
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
normalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
viewDirection = vec3(modelMatrix * gl_Vertex
- vec4(_WorldSpaceCameraPos, 1.0));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 reflectedDirection =
reflect(viewDirection, normalize(normalDirection));
gl_FragColor = textureCube(_Cube, reflectedDirection);
}
#endif
ENDGLSL
}
}
}
Summary
[edit | edit source]Congratulations! You have reached the end of the first tutorial on environment maps. We have seen:
- How to compute the reflection of a skybox in an object.
- How to generate cube maps in Unity and how to use them for reflection mapping.
Further Reading
[edit | edit source]If you still want to know more
- about the reflection of vectors, you should read Section “Specular Highlights”.
- about cube maps in Unity, you should read Unity's documentation about cube maps.
Curved Glass
[edit | edit source]
This tutorial covers refraction mapping and its implementation with cube maps.
It is a variation of Section “Reflecting Surfaces”, which should be read first.
Refraction Mapping
[edit | edit source]In Section “Reflecting Surfaces”, we reflected view rays and then performed texture lookups in a cube map in the reflected direction. Here, we refract view rays at a curved, transparent surface and then perform the lookups with the refracted direction. The effect will ignore the second refraction when the ray leaves the transparent object again; however, many people hardly notice the differences since such refractions are usually not part of our daily life.
Instead of the reflect function, we are using the refract function; thus, the fragment shader could be:
#ifdef FRAGMENT
void main()
{
float refractiveIndex = 1.5;
vec3 refractedDirection = refract(normalize(viewDirection),
normalize(normalDirection), 1.0 / refractiveIndex);
gl_FragColor = textureCube(_Cube, refractedDirection);
}
#endif
Note that refract takes a third argument, which is the refractive index of the outside medium (e.g. 1.0 for air) divided by the refractive index of the object (e.g. 1.5 for some kinds of glass). Also note that the first argument has to be normalized, which isn't necessary for reflect.
Complete Shader Code
[edit | edit source]With the adapted fragment shader, the complete shader code becomes:
Shader "GLSL shader with refraction mapping" {
Properties {
_Cube ("Environment Map", Cube) = "" {}
}
SubShader {
Pass {
GLSLPROGRAM
// User-specified uniforms
uniform samplerCube _Cube;
// The following built-in uniforms
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
// Varyings
varying vec3 normalDirection;
varying vec3 viewDirection;
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
normalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
viewDirection = vec3(modelMatrix * gl_Vertex
- vec4(_WorldSpaceCameraPos, 1.0));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
float refractiveIndex = 1.5;
vec3 refractedDirection = refract(normalize(viewDirection),
normalize(normalDirection), 1.0 / refractiveIndex);
gl_FragColor = textureCube(_Cube, refractedDirection);
}
#endif
ENDGLSL
}
}
}
Summary
[edit | edit source]Congratulations. This is the end of another tutorial. We have seen:
- How to adapt reflection mapping to refraction mapping using the
refractinstruction.
Further Reading
[edit | edit source]If you still want to know more
- about reflection mapping and cube maps, you should read Section “Reflecting Surfaces”.
- about the
refractinstruction, you could look it up in the “OpenGL ES Shading Language 1.0.17 Specification” available at the “Khronos OpenGL ES API Registry”.
Skyboxes
[edit | edit source]
This tutorial covers the rendering of environment maps as backgrounds with the help of cube maps.
It is based on Section “Reflecting Surfaces”. If you haven't read that tutorial, this would be a very good time to read it.
Rendering a Skybox in the Background
[edit | edit source]As explained in Section “Reflecting Surfaces”, a skybox can be thought of as an infinitely large, textured box that surrounds a scene. Sometimes, skyboxes (or skydomes) are implemented by sufficiently large textured models, which approximate an infinitely large box (or dome). However, Section “Reflecting Surfaces” introduced the concept of a cube map, which actually represents an infinitely large box; thus, we don't need the approximation of a box or a dome of limited size. Instead, we can render any screen-filling model (it doesn't matter whether it is a box, a dome, or an apple tree as long as it covers the whole background), compute the view vector from the camera to the rasterized surface point in the vertex shader (as we did in Section “Reflecting Surfaces”) and then perform a lookup in the cube map with this view vector (instead of the reflected view vector in Section “Reflecting Surfaces”) in the fragment shader:
#ifdef FRAGMENT
void main()
{
gl_FragColor = textureCube(_Cube, viewDirection);
}
#endif
For best performance we should, of course, render a model with only a few vertices and each pixel should be rasterized only once. Thus, rendering the inside of a cube that surrounds the camera (or the whole scene) is fine.
Complete Shader Code
[edit | edit source]The shader should be attached to a material, which should be attached to a cube that surrounds the camera. In the shader code, we deactivate writing to the depth buffer with ZWrite Off such that no objects are occluded by the skybox. (See the description of the depth test in Section “Per-Fragment Operations”.) Front-face culling is activated with Cull Front such that only the “inside” of the cube is rasterized. (See Section “Cutaways”.) The line Tags { "Queue" = "Background" } instructs Unity to render this pass before other objects are rendered.
Shader "GLSL shader for skybox" {
Properties {
_Cube ("Environment Map", Cube) = "" {}
}
SubShader {
Tags { "Queue" = "Background" }
Pass {
ZWrite Off
Cull Front
GLSLPROGRAM
// User-specified uniform
uniform samplerCube _Cube;
// The following built-in uniforms
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
// Varying
varying vec3 viewDirection;
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
viewDirection = vec3(modelMatrix * gl_Vertex
- vec4(_WorldSpaceCameraPos, 1.0));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = textureCube(_Cube, viewDirection);
}
#endif
ENDGLSL
}
}
}
Shader Code for Unity's Skybox System
[edit | edit source]The shader above illustrates how to render a skybox by rendering a cube around the camera with a specific shader. This is a very general approach. Unity, however, has its own skybox system that doesn't require any game object: you just specify the material with the skybox shader in the main menu Edit > Render Settings > Skybox Material and Unity takes care of the rest. Unfortunately, we cannot use our shader for this system since we have to do the lookup in the cube texture at the position that is specified by the vertex texture coordinates. This is actually easier than computing the view direction. Here is the code:
Shader "GLSL shader for skybox" {
Properties {
_Cube ("Environment Map", Cube) = "" {}
}
SubShader {
Tags { "Queue" = "Background" }
Pass {
ZWrite Off
Cull Off
GLSLPROGRAM
#extension GL_NV_shadow_samplers_cube : enable
// User-specified uniform
uniform samplerCube _Cube;
// Varying
varying vec3 texCoords;
#ifdef VERTEX
void main()
{
texCoords = vec3(gl_MultiTexCoord0);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = textureCube(_Cube, texCoords);
}
#endif
ENDGLSL
}
}
}
As mentioned above, you should create a material with this shader and drag the material to Edit > Render Settings > Skybox Material. There is no need to attach the material to any game object.
Summary
[edit | edit source]Congratulations, you have reached the end of another tutorial! We have seen:
- How to render skyboxes.
- How to render skyboxes in Unity without game objects.
Further Reading
[edit | edit source]If you still want to know more
- about cube maps and reflections of skyboxes in objects, you should read Section “Reflecting Surfaces”.
- about lighting that is consistent with a skybox, you should read Section “Many Light Sources”.
Many Light Sources
[edit | edit source]
This tutorial introduces image-based lighting, in particular diffuse (irradiance) environment mapping and its implementation with cube maps.
This tutorial is based on Section “Reflecting Surfaces”. If you haven't read that tutorial, this would be a very good time to read it.
Diffuse Lighting by Many Lights
[edit | edit source]Consider the lighting of the sculpture in the image to the left. There is natural light coming through the windows. Some of this light bounces off the floor, walls and visitors before reaching the sculpture. Additionally, there are artificial light sources, and their light is also shining directly and indirectly onto the sculpture. How many directional lights and point lights would be needed to simulate this kind of complex lighting environment convincingly? At least more than a handful (probably more than a dozen) and therefore the performance of the lighting computations is challenging.
This problem is addressed by image-based lighting. For static lighting environments that are described by an environment map, e.g. a cube map, image-based lighting allows us to compute the lighting by an arbitrary number of light sources with a single texture lookup in a cube map (see Section “Reflecting Surfaces” for a description of cube maps). How does it work?
In this section we focus on diffuse lighting. Assume that every texel (i.e. pixel) of a cube map acts as a directional light source. (Remember that cube maps are usually assumed to be infinitely large such that only directions matter, but positions don't.) The resulting lighting for a given surface normal direction can be computed as described in Section “Diffuse Reflection”. It's basically the cosine between the surface normal vector N and the vector to the light source L:
Since the texels are the light sources, L is just the direction from the center of the cube to the center of the texel in the cube map. A small cube map with 32×32 texels per face has already 32×32×6 = 6144 texels. Adding the illumination by thousands of light sources is not going to work in real time. However, for a static cube map we can compute the diffuse illumination for all possible surface normal vectors N in advance and store them in a lookup table. When lighting a point on a surface with a specific surface normal vector, we can then just look up the diffuse illumination for the specific surface normal vector N in that precomputed lookup table.
Thus, for a specific surface normal vector N we add (i.e. integrate) the diffuse illumination by all texels of the cube map. We store the resulting diffuse illumination for this surface normal vector in a second cube map (the “diffuse irradiance environment map” or “diffuse environment map” for short). This second cube map will act as a lookup table, where each direction (i.e. surface normal vector) is mapped to a color (i.e. diffuse illumination by potentially thousands of light sources). The fragment shader is therefore really simple (this one could use the vertex shader from Section “Reflecting Surfaces”):
#ifdef FRAGMENT
void main()
{
gl_FragColor = textureCube(_Cube, normalDirection);
}
#endif
It is just a lookup of the precomputed diffuse illumination using the surface normal vector of the rasterized surface point. However, the precomputation of the diffuse environment map is somewhat more complicated as described in the next section.
Computation of Diffuse Environment Maps
[edit | edit source]This section presents some JavaScript code to illustrate the computation of cube maps for diffuse (irradiance) environment maps. In order to use it in Unity, choose Create > JavaScript in the Project View. Then open the script in Unity's text editor, copy the JavaScript code into it, and attach the script to the game object that has a material with the shader presented below. When a new cube map of sufficiently small dimensions is specified for the shader property _OriginalCube (which is labeled Environment Map in the shader user interface), the script will update the shader property _Cube (i.e. Diffuse Environment Map in the user interface) with a corresponding diffuse environment map. Note that the script only accepts cube maps of face dimensions 32×32 or smaller because the computation time tends to be very long for larger cube maps. Thus, when creating a cube map in Unity, make sure to choose a sufficiently small size.
The script includes only a handful of functions: Awake() initializes the variables; Update() takes care of communicating with the user and the material (i.e. reading and writing shader properties); computeFilteredCubemap() does the actual work of computing the diffuse environment map; and getDirection() is a small utility function for computeFilteredCubemap() to compute the direction associated with each texel of a cube map. Note that computeFilteredCubemap() not only integrates the diffuse illumination but also avoids discontinuous seams between faces of the cube map by setting neighboring texels along the seams to the same averaged color.
@script ExecuteInEditMode()
private var originalCubemap : Cubemap; // a reference to the
// environment map specified in the shader by the user
private var filteredCubemap : Cubemap; // the diffuse irradiance
// environment map computed by this script
function Update()
{
var originalTexture : Texture =
renderer.sharedMaterial.GetTexture("_OriginalCube");
// get the user-specified environment map
if (originalTexture == null)
// did the user specify "None" for the environment map?
{
if (originalCubemap != null)
{
originalCubemap = null;
filteredCubemap = null;
renderer.sharedMaterial.SetTexture("_Cube", null);
}
return;
}
else if (originalTexture == originalCubemap
&& filteredCubemap != null
&& null == renderer.sharedMaterial.GetTexture("_Cube"))
{
renderer.sharedMaterial.SetTexture("_Cube", filteredCubemap);
// set the computed diffuse environment map in the shader
}
else if (originalTexture != originalCubemap
|| filteredCubemap
!= renderer.sharedMaterial.GetTexture("_Cube"))
// has the user specified a cube map that is different of
// what we had processed previously?
{
if (EditorUtility.DisplayDialog("Processing of Environment Map",
"Do you want to process the cube map of face size "
+ originalTexture.width + "x" + originalTexture.width
+ "? (This will take some time.)",
"OK", "Cancel"))
// does the user really want to process this cube map?
{
originalCubemap = originalTexture;
if (filteredCubemap
!= renderer.sharedMaterial.GetTexture("_Cube"))
{
if (null != renderer.sharedMaterial.GetTexture("_Cube"))
{
DestroyImmediate(renderer.sharedMaterial.GetTexture(
"_Cube")); // clean up
}
}
if (null != filteredCubemap)
{
DestroyImmediate(filteredCubemap); // clean up
}
computeFilteredCubemap();
// compute the diffuse environment map
renderer.sharedMaterial.SetTexture("_Cube", filteredCubemap);
// set the computed diffuse environment map in the shader
}
else // no cancel the processing and reset everything
{
originalCubemap = null;
filteredCubemap = null;
renderer.sharedMaterial.SetTexture("_OriginalCube", null);
renderer.sharedMaterial.SetTexture("_Cube", null);
}
}
return;
}
function computeFilteredCubemap()
// This function computes a diffuse environment map in
// "filteredCubemap" of the same dimensions as "originalCubemap"
// by integrating -- for each texel of "filteredCubemap" --
// the diffuse illumination from all texels of "originalCubemap"
// for the surface normal vector corresponding to the direction
// of each texel of "filteredCubemap".
{
filteredCubemap = Cubemap(originalCubemap.width,
originalCubemap.format, true);
// create the diffuse environment cube map
var filteredSize : int = filteredCubemap.width;
var originalSize : int = originalCubemap.width;
// compute all texels of the diffuse environment
// cube map by iterating over all of them
for (var filteredFace : int = 0; filteredFace < 6; filteredFace++)
{
for (var filteredI : int = 0; filteredI < filteredSize; filteredI++)
{
for (var filteredJ : int = 0; filteredJ < filteredSize; filteredJ++)
{
var filteredDirection : Vector3 =
getDirection(filteredFace,
filteredI, filteredJ, filteredSize).normalized;
var totalWeight : float = 0.0;
var originalDirection : Vector3;
var originalFaceDirection : Vector3;
var weight : float;
var filteredColor : Color = Color(0.0, 0.0, 0.0);
// sum (i.e. integrate) the diffuse illumination
// by all texels in the original environment map
for (var originalFace : int = 0; originalFace < 6; originalFace++)
{
originalFaceDirection = getDirection(originalFace,
1, 1, 3).normalized; // the normal vector of the face
for (var originalI : int = 0; originalI < originalSize; originalI++)
{
for (var originalJ : int = 0; originalJ < originalSize; originalJ++)
{
originalDirection = getDirection(originalFace,
originalI, originalJ, originalSize);
// direction to the texel, i.e. light source
weight = 1.0 / originalDirection.sqrMagnitude;
// take smaller size of more distant texels
// into account
originalDirection = originalDirection.normalized;
weight = weight
* Vector3.Dot(originalFaceDirection,
originalDirection); // take tilt of texels
// compared to face into account
weight = weight * Mathf.Max(0.0,
Vector3.Dot(filteredDirection,
originalDirection));
// directional filter for diffuse illumination
totalWeight = totalWeight + weight;
// instead of analytically normalization,
// we just normalize to the potentially
// maximum illumination
filteredColor = filteredColor +
weight * originalCubemap.GetPixel(originalFace,
originalI, originalJ);
// add the illumination by this texel
}
}
}
filteredCubemap.SetPixel(filteredFace, filteredI,
filteredJ, filteredColor / totalWeight);
// store the diffuse illumination of this texel
}
}
}
// Avoid seams between cube faces:
// average edge texels to the same color on both sides of the seam
// (except corner texels, see below)
var maxI : int = filteredCubemap.width - 1;
var average : Color;
for (var i : int = 1; i < maxI; i++)
{
average = (filteredCubemap.GetPixel(0, i, 0)
+ filteredCubemap.GetPixel(2, maxI, maxI - i)) / 2.0;
filteredCubemap.SetPixel(0, i, 0, average);
filteredCubemap.SetPixel(2, maxI, maxI - i, average);
average = (filteredCubemap.GetPixel(0, 0, i)
+ filteredCubemap.GetPixel(4, maxI, i)) / 2.0;
filteredCubemap.SetPixel(0, 0, i, average);
filteredCubemap.SetPixel(4, maxI, i, average);
average = (filteredCubemap.GetPixel(0, i, maxI)
+ filteredCubemap.GetPixel(3, maxI, i)) / 2.0;
filteredCubemap.SetPixel(0, i, maxI, average);
filteredCubemap.SetPixel(3, maxI, i, average);
average = (filteredCubemap.GetPixel(0, maxI, i)
+ filteredCubemap.GetPixel(5, 0, i)) / 2.0;
filteredCubemap.SetPixel(0, maxI, i, average);
filteredCubemap.SetPixel(5, 0, i, average);
average = (filteredCubemap.GetPixel(1, i, 0)
+ filteredCubemap.GetPixel(2, 0, i)) / 2.0;
filteredCubemap.SetPixel(1, i, 0, average);
filteredCubemap.SetPixel(2, 0, i, average);
average = (filteredCubemap.GetPixel(1, 0, i)
+ filteredCubemap.GetPixel(5, maxI, i)) / 2.0;
filteredCubemap.SetPixel(1, 0, i, average);
filteredCubemap.SetPixel(5, maxI, i, average);
average = (filteredCubemap.GetPixel(1, i, maxI)
+ filteredCubemap.GetPixel(3, 0, maxI - i)) / 2.0;
filteredCubemap.SetPixel(1, i, maxI, average);
filteredCubemap.SetPixel(3, 0, maxI - i, average);
average = (filteredCubemap.GetPixel(1, maxI, i)
+ filteredCubemap.GetPixel(4, 0, i)) / 2.0;
filteredCubemap.SetPixel(1, maxI, i, average);
filteredCubemap.SetPixel(4, 0, i, average);
average = (filteredCubemap.GetPixel(2, i, 0)
+ filteredCubemap.GetPixel(5, maxI - i, 0)) / 2.0;
filteredCubemap.SetPixel(2, i, 0, average);
filteredCubemap.SetPixel(5, maxI - i, 0, average);
average = (filteredCubemap.GetPixel(2, i, maxI)
+ filteredCubemap.GetPixel(4, i, 0)) / 2.0;
filteredCubemap.SetPixel(2, i, maxI, average);
filteredCubemap.SetPixel(4, i, 0, average);
average = (filteredCubemap.GetPixel(3, i, 0)
+ filteredCubemap.GetPixel(4, i, maxI)) / 2.0;
filteredCubemap.SetPixel(3, i, 0, average);
filteredCubemap.SetPixel(4, i, maxI, average);
average = (filteredCubemap.GetPixel(3, i, maxI)
+ filteredCubemap.GetPixel(5, maxI - i, maxI)) / 2.0;
filteredCubemap.SetPixel(3, i, maxI, average);
filteredCubemap.SetPixel(5, maxI - i, maxI, average);
}
// Avoid seams between cube faces: average corner texels
// to the same color on all three faces meeting in one corner
average = (filteredCubemap.GetPixel(0, 0, 0)
+ filteredCubemap.GetPixel(2, maxI, maxI)
+ filteredCubemap.GetPixel(4, maxI, 0)) / 3.0;
filteredCubemap.SetPixel(0, 0, 0, average);
filteredCubemap.SetPixel(2, maxI, maxI, average);
filteredCubemap.SetPixel(4, maxI, 0, average);
average = (filteredCubemap.GetPixel(0, maxI, 0)
+ filteredCubemap.GetPixel(2, maxI, 0)
+ filteredCubemap.GetPixel(5, 0, 0)) / 3.0;
filteredCubemap.SetPixel(0, maxI, 0, average);
filteredCubemap.SetPixel(2, maxI, 0, average);
filteredCubemap.SetPixel(5, 0, 0, average);
average = (filteredCubemap.GetPixel(0, 0, maxI)
+ filteredCubemap.GetPixel(3, maxI, 0)
+ filteredCubemap.GetPixel(4, maxI, maxI)) / 3.0;
filteredCubemap.SetPixel(0, 0, maxI, average);
filteredCubemap.SetPixel(3, maxI, 0, average);
filteredCubemap.SetPixel(4, maxI, maxI, average);
average = (filteredCubemap.GetPixel(0, maxI, maxI)
+ filteredCubemap.GetPixel(3, maxI, maxI)
+ filteredCubemap.GetPixel(5, 0, maxI)) / 3.0;
filteredCubemap.SetPixel(0, maxI, maxI, average);
filteredCubemap.SetPixel(3, maxI, maxI, average);
filteredCubemap.SetPixel(5, 0, maxI, average);
average = (filteredCubemap.GetPixel(1, 0, 0)
+ filteredCubemap.GetPixel(2, 0, 0)
+ filteredCubemap.GetPixel(5, maxI, 0)) / 3.0;
filteredCubemap.SetPixel(1, 0, 0, average);
filteredCubemap.SetPixel(2, 0, 0, average);
filteredCubemap.SetPixel(5, maxI, 0, average);
average = (filteredCubemap.GetPixel(1, maxI, 0)
+ filteredCubemap.GetPixel(2, 0, maxI)
+ filteredCubemap.GetPixel(4, 0, 0)) / 3.0;
filteredCubemap.SetPixel(1, maxI, 0, average);
filteredCubemap.SetPixel(2, 0, maxI, average);
filteredCubemap.SetPixel(4, 0, 0, average);
average = (filteredCubemap.GetPixel(1, 0, maxI)
+ filteredCubemap.GetPixel(3, 0, maxI)
+ filteredCubemap.GetPixel(5, maxI, maxI)) / 3.0;
filteredCubemap.SetPixel(1, 0, maxI, average);
filteredCubemap.SetPixel(3, 0, maxI, average);
filteredCubemap.SetPixel(5, maxI, maxI, average);
average = (filteredCubemap.GetPixel(1, maxI, maxI)
+ filteredCubemap.GetPixel(3, 0, 0)
+ filteredCubemap.GetPixel(4, 0, maxI)) / 3.0;
filteredCubemap.SetPixel(1, maxI, maxI, average);
filteredCubemap.SetPixel(3, 0, 0, average);
filteredCubemap.SetPixel(4, 0, maxI, average);
filteredCubemap.Apply();
// apply all the texture.SetPixel(...) commands
}
function getDirection(face : int, i : int, j : int, size : int)
: Vector3
// This function computes the direction that is
// associated with a texel of a cube map
{
var direction : Vector3;
if (face == 0)
{
direction = Vector3(0.5,
-((j + 0.5) / size - 0.5), -((i + 0.5) / size - 0.5));
}
else if (face == 1)
{
direction = Vector3(-0.5,
-((j + 0.5) / size - 0.5), ((i + 0.5) / size - 0.5));
}
else if (face == 2)
{
direction = Vector3(((i + 0.5) / size - 0.5),
0.5, ((j + 0.5) / size - 0.5));
}
else if (face == 3)
{
direction = Vector3(((i + 0.5) / size - 0.5),
-0.5, -((j + 0.5) / size - 0.5));
}
else if (face == 4)
{
direction = Vector3(((i + 0.5) / size - 0.5),
-((j + 0.5) / size - 0.5), 0.5);
}
else if (face == 5)
{
direction = Vector3(-((i + 0.5) / size - 0.5),
-((j + 0.5) / size - 0.5), -0.5);
}
return direction;
}
As an alternative to the JavaScript code above, you can also use the following C# code.
using UnityEngine;
using UnityEditor;
using System.Collections;
[ExecuteInEditMode]
public class ComputeDiffuseEnvironmentMap : MonoBehaviour
{
public Cubemap originalCubeMap;
// environment map specified in the shader by the user
//[System.Serializable]
// avoid being deleted by the garbage collector,
// and thus leaking
private Cubemap filteredCubeMap;
// the computed diffuse irradience environment map
private void Update()
{
Cubemap originalTexture = null;
try
{
originalTexture = renderer.sharedMaterial.GetTexture(
"_OriginalCube") as Cubemap;
}
catch (System.Exception)
{
Debug.LogError("'_OriginalCube' not found on shader. "
+ "Are you using the wrong shader?");
return;
}
if (originalTexture == null)
// did the user set "none" for the map?
{
if (originalCubeMap != null)
{
renderer.sharedMaterial.SetTexture("_Cube", null);
originalCubeMap = null;
filteredCubeMap = null;
return;
}
}
else if (originalTexture == originalCubeMap
&& filteredCubeMap != null
&& renderer.sharedMaterial.GetTexture("_Cube") == null)
{
renderer.sharedMaterial.SetTexture("_Cube",
filteredCubeMap); // set the computed
// diffuse environment map in the shader
}
else if (originalTexture != originalCubeMap
|| filteredCubeMap
!= renderer.sharedMaterial.GetTexture("_Cube"))
{
if (EditorUtility.DisplayDialog(
"Processing of Environment Map",
"Do you want to process the cube map of face size "
+ originalTexture.width + "x" + originalTexture.width
+ "? (This will take some time.)",
"OK", "Cancel"))
{
if (filteredCubeMap
!= renderer.sharedMaterial.GetTexture("_Cube"))
{
if (renderer.sharedMaterial.GetTexture("_Cube")
!= null)
{
DestroyImmediate(
renderer.sharedMaterial.GetTexture(
"_Cube")); // clean up
}
}
if (filteredCubeMap != null)
{
DestroyImmediate(filteredCubeMap); // clean up
}
originalCubeMap = originalTexture;
filteredCubeMap = computeFilteredCubeMap();
//computes the diffuse environment map
renderer.sharedMaterial.SetTexture("_Cube",
filteredCubeMap); // set the computed
// diffuse environment map in the shader
return;
}
else
{
originalCubeMap = null;
filteredCubeMap = null;
renderer.sharedMaterial.SetTexture("_Cube", null);
renderer.sharedMaterial.SetTexture(
"_OriginalCube", null);
}
}
}
// This function computes a diffuse environment map in
// "filteredCubemap" of the same dimensions as "originalCubemap"
// by integrating -- for each texel of "filteredCubemap" --
// the diffuse illumination from all texels of "originalCubemap"
// for the surface normal vector corresponding to the direction
// of each texel of "filteredCubemap".
private Cubemap computeFilteredCubeMap()
{
Cubemap filteredCubeMap = new Cubemap(originalCubeMap.width,
originalCubeMap.format, true);
int filteredSize = filteredCubeMap.width;
int originalSize = originalCubeMap.width;
// Compute all texels of the diffuse environment cube map
// by itterating over all of them
for (int filteredFace = 0; filteredFace < 6; filteredFace++)
// the six sides of the cube
{
for (int filteredI = 0; filteredI < filteredSize; filteredI++)
{
for (int filteredJ = 0; filteredJ < filteredSize; filteredJ++)
{
Vector3 filteredDirection =
getDirection(filteredFace,
filteredI, filteredJ, filteredSize).normalized;
float totalWeight = 0.0f;
Vector3 originalDirection;
Vector3 originalFaceDirection;
float weight;
Color filteredColor = new Color(0.0f, 0.0f, 0.0f);
// sum (i.e. integrate) the diffuse illumination
// by all texels in the original environment map
for (int originalFace = 0; originalFace < 6; originalFace++)
{
originalFaceDirection = getDirection(
originalFace, 1, 1, 3).normalized;
//the normal vector of the face
for (int originalI = 0; originalI < originalSize; originalI++)
{
for (int originalJ = 0; originalJ < originalSize; originalJ++)
{
originalDirection = getDirection(
originalFace, originalI,
originalJ, originalSize);
// direction to the texel
// (i.e. light source)
weight = 1.0f
/ originalDirection.sqrMagnitude;
// take smaller size of more
// distant texels into account
originalDirection =
originalDirection.normalized;
weight = weight * Vector3.Dot(
originalFaceDirection,
originalDirection);
// take tilt of texel compared
// to face into account
weight = weight * Mathf.Max(0.0f,
Vector3.Dot(filteredDirection,
originalDirection));
// directional filter
// for diffuse illumination
totalWeight = totalWeight + weight;
// instead of analytically
// normalization, we just normalize
// to the potential max illumination
filteredColor = filteredColor + weight
* originalCubeMap.GetPixel(
(CubemapFace)originalFace,
originalI, originalJ); // add the
// illumination by this texel
}
}
}
filteredCubeMap.SetPixel(
(CubemapFace)filteredFace, filteredI,
filteredJ, filteredColor / totalWeight);
// store the diffuse illumination of this texel
}
}
}
// Avoid seams between cube faces: average edge texels
// to the same color on each side of the seam
int maxI = filteredCubeMap.width - 1;
for (int i = 0; i < maxI; i++)
{
setFaceAverage(ref filteredCubeMap,
0, i, 0, 2, maxI, maxI - i);
setFaceAverage(ref filteredCubeMap,
0, 0, i, 4, maxI, i);
setFaceAverage(ref filteredCubeMap,
0, i, maxI, 3, maxI, i);
setFaceAverage(ref filteredCubeMap,
0, maxI, i, 5, 0, i);
setFaceAverage(ref filteredCubeMap,
1, i, 0, 2, 0, i);
setFaceAverage(ref filteredCubeMap,
1, 0, i, 5, maxI, i);
setFaceAverage(ref filteredCubeMap,
1, i, maxI, 3, 0, maxI - i);
setFaceAverage(ref filteredCubeMap,
1, maxI, i, 4, 0, i);
setFaceAverage(ref filteredCubeMap,
2, i, 0, 5, maxI - i, 0);
setFaceAverage(ref filteredCubeMap,
2, i, maxI, 4, i, 0);
setFaceAverage(ref filteredCubeMap,
3, i, 0, 4, i, maxI);
setFaceAverage(ref filteredCubeMap,
3, i, maxI, 5, maxI - i, maxI);
}
// Avoid seams between cube faces:
// average corner texels to the same color
// on all three faces meeting in one corner
setCornerAverage(ref filteredCubeMap,
0, 0, 0, 2, maxI, maxI, 4, maxI, 0);
setCornerAverage(ref filteredCubeMap,
0, maxI, 0, 2, maxI, 0, 5, 0, 0);
setCornerAverage(ref filteredCubeMap,
0, 0, maxI, 3, maxI, 0, 4, maxI, maxI);
setCornerAverage(ref filteredCubeMap,
0, maxI, maxI, 3, maxI, maxI, 5, 0, maxI);
setCornerAverage(ref filteredCubeMap,
1, 0, 0, 2, 0, 0, 5, maxI, 0);
setCornerAverage(ref filteredCubeMap,
1, maxI, 0, 2, 0, maxI, 4, 0, 0);
setCornerAverage(ref filteredCubeMap,
1, 0, maxI, 3, 0, maxI, 5, maxI, maxI);
setCornerAverage(ref filteredCubeMap,
1, maxI, maxI, 3, 0, 0, 4, 0, maxI);
filteredCubeMap.Apply(); //apply all SetPixel(..) commands
return filteredCubeMap;
}
private void setFaceAverage(ref Cubemap filteredCubeMap,
int a, int b, int c, int d, int e, int f)
{
Color average =
(filteredCubeMap.GetPixel((CubemapFace)a, b, c)
+ filteredCubeMap.GetPixel((CubemapFace)d, e, f)) / 2.0f;
filteredCubeMap.SetPixel((CubemapFace)a, b, c, average);
filteredCubeMap.SetPixel((CubemapFace)d, e, f, average);
}
private void setCornerAverage(ref Cubemap filteredCubeMap,
int a, int b, int c, int d, int e, int f, int g, int h, int i)
{
Color average =
(filteredCubeMap.GetPixel((CubemapFace)a, b, c)
+ filteredCubeMap.GetPixel((CubemapFace)d, e, f)
+ filteredCubeMap.GetPixel((CubemapFace)g, h, i)) / 3.0f;
filteredCubeMap.SetPixel((CubemapFace)a, b, c, average);
filteredCubeMap.SetPixel((CubemapFace)d, e, f, average);
filteredCubeMap.SetPixel((CubemapFace)g, h, i, average);
}
private Vector3 getDirection(int face, int i, int j, int size)
{
switch (face)
{
case 0:
return new Vector3(0.5f,
-((j + 0.5f) / size - 0.5f),
-((i + 0.5f) / size - 0.5f));
case 1:
return new Vector3(-0.5f,
-((j + 0.5f) / size - 0.5f),
((i + 0.5f) / size - 0.5f));
case 2:
return new Vector3(((i + 0.5f) / size - 0.5f),
0.5f, ((j + 0.5f) / size - 0.5f));
case 3:
return new Vector3(((i + 0.5f) / size - 0.5f),
-0.5f, -((j + 0.5f) / size - 0.5f));
case 4:
return new Vector3(((i + 0.5f) / size - 0.5f),
-((j + 0.5f) / size - 0.5f), 0.5f);
case 5:
return new Vector3(-((i + 0.5f) / size - 0.5f),
-((j + 0.5f) / size - 0.5f), -0.5f);
default:
return Vector3.zero;
}
}
}
Complete Shader Code
[edit | edit source]As promised, the actual shader code is very short; the vertex shader is a reduced version of the vertex shader of Section “Reflecting Surfaces”:
Shader "GLSL shader with image-based diffuse lighting" {
Properties {
_OriginalCube ("Environment Map", Cube) = "" {}
_Cube ("Diffuse Environment Map", Cube) = "" {}
}
SubShader {
Pass {
GLSLPROGRAM
// Uniform specified by the user or by a script
uniform samplerCube _Cube; // the diffuse environment map
// The following built-in uniforms
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _World2Object; // inverse model matrix
// Varyings
varying vec3 normalDirection;
#ifdef VERTEX
void main()
{
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
normalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = textureCube(_Cube, normalDirection);
}
#endif
ENDGLSL
}
}
}
Changes for Specular (i.e. Glossy) Reflection
[edit | edit source]The shader and script above are sufficient to compute diffuse illumination by a large number of static, directional light sources. But what about the specular illumination discussed in Section “Specular Highlights”, i.e.:
First, we have to rewrite this equation such that it depends only on the direction to the light source L and the reflected view vector R:
With this equation, we can compute a lookup table (i.e. a cube map) that contains the specular illumination by many light sources for any reflected view vector R. In order to look up the specular illumination with such a table, we just need to compute the reflected view vector and perform a texture lookup in a cube map. In fact, this is exactly what the shader code of Section “Reflecting Surfaces” does. Thus, we actually only need to compute the lookup table.
It turns out that the JavaScript code presented above can be easily adapted to compute such a lookup table. All we have to do is to change the line
weight = weight * Mathf.Max(0.0,
Vector3.Dot(filteredDirection, originalDirection));
// directional filter for diffuse illumination
to
weight = weight * Mathf.Pow(Mathf.Max(0.0,
Vector3.Dot(filteredDirection, originalDirection)), 50.0);
// directional filter for specular illumination
where 50.0 should be replaced by a variable for . This allows us to compute lookup tables for any specific shininess. (The same cube map could be used for varying values of the shininess if the mipmap-level was specified explicitly using the textureCubeLod instruction in the shader; however, this technique is beyond the scope of this tutorial.)
Summary
[edit | edit source]Congratulations, you have reached the end of a rather advanced tutorial! We have seen:
- What image-based rendering is about.
- How to compute and use a cube map to implement a diffuse environment map.
- How to adapt the code for specular reflection.
Further Reading
[edit | edit source]If you still want to know more
- about cube maps, you should read Section “Reflecting Surfaces”.
- about (dynamic) diffuse environment maps, you could read Chapter 10, “Real-Time Computation of Dynamic Irradiance Environment Maps” by Gary King of the book “GPU Gems 2” by Matt Pharr (editor) published 2005 by Addison-Wesley, which is available online.
Brushed Metal
[edit | edit source]
This tutorial covers anisotropic specular highlights.
It is one of several tutorials about lighting that go beyond the Phong reflection model. However, it is based on lighting with the Phong reflection model as described in Section “Specular Highlights” (for per-vertex lighting) and Section “Smooth Specular Highlights” (for per-pixel lighting). If you haven't read those tutorials yet, you should read them first.
While the Phong reflection model is reasonably good for paper, plastics, and some other materials with isotropic reflection (i.e. round highlights), this tutorial looks specifically at materials with anisotropic reflection (i.e. non-round highlights), for example brushed aluminium as in the photo to the left.

Ward's Model of Anisotropic Reflection
[edit | edit source]Gregory Ward published a suitable model of anisotropic reflection in his work “Measuring and Modeling Anisotropic Reflection”, Computer Graphics (SIGGRAPH ’92 Proceedings), pp. 265–272, July 1992. (A copy of the paper is available online.) This model describes the reflection in terms of a BRDF (bidrectional reflectance distribution function), which is a four-dimensional function that describes how a light ray from any direction is reflected into any other direction. His BRDF model consists of two terms: a diffuse reflectance term, which is , and a more complicated specular reflectance term.
Let's have a look at the diffuse term first: is just a constant (about 3.14159) and specifies the diffuse reflectance. In principle, a reflectance for each wave length is necessary; however, usually one reflectance for each of the three color components (red, green, and blue) is specified. If we include the constant , just represents the diffuse material color , which we have first seen in Section “Diffuse Reflection” but which also appears in the Phong reflection model (see Section “Specular Highlights”). You might wonder why the factor max(0, L·N) doesn't appear in the BRDF. The answer is that the BRDF is defined in such a way that this factor is not included in it (because it isn't really a property of the material) but it should be multiplied with the BRDF when doing any lighting computation.
Thus, in order to implement a given BRDF for opaque materials, we have to multiply all terms of the BRDF with max(0, L·N) and − unless we want to implement physically correct lighting − we can replace any constant factors by user-specified colors, which usually are easier to control than physical quantities.
For the specular term of his BRDF model, Ward presents an approximation in equation 5b of his paper. I adapted it slightly such that it uses the normalized surface normal vector N, the normalized direction to the viewer V, the normalized direction to the light source L, and the normalized halfway vector H which is (V + L) / |V + L|. Using these vectors, Ward's approximation for the specular term becomes:
Here, is the specular reflectance, which describes the color and intensity of the specular highlights; and are material constants that describe the shape and size of the highlights. Since all these variables are material constants, we can combine them in one constant . Thus, we get a slightly shorter version:
Remember that we still have to multiply this BRDF term with L·N when implementing it in a shader and set it to 0 if L·N is less than 0. Furthermore, it should also be 0 if V·N is less than 0, i.e., if we are looking at the surface from the “wrong” side.
There are two vectors that haven't been described yet: T and B. T is the brush direction on the surface and B is orthogonal to T but also on the surface. Unity provides us with a tangent vector on the surface as a vertex attribute (see Section “Debugging of Shaders”), which we will use as the vector T. Computing the cross product of N and T generates a vector B, which is orthogonal to N and T, as it should be.
Implementation of Ward's BRDF Model
[edit | edit source]We base our implementation on the shader for per-pixel lighting in Section “Smooth Specular Highlights”. We need another varying variable tangentDirection for the tangent vector T (i.e. the brush direction) and we compute two more directions: halfwayVector for the halfway vector H and binormalDirection for the binormal vector B. The properties are _Color for , _SpecColor for , _AlphaX for , and _AlphaY for .
The fragment shader is then very similar to the version in Section “Smooth Specular Highlights” except that it normalizes tangentDirection, computes halfwayVector and binormalDirection, and implements a different equation for the specular part. Furthermore, this shader computs the dot product L·N only once and stores it in dotLN such that it can be reused without having to recompute it. It looks like this:
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 tangentDirection = normalize(varyingTangentDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 halfwayVector =
normalize(lightDirection + viewDirection);
vec3 binormalDirection =
cross(normalDirection, tangentDirection);
float dotLN = dot(lightDirection, normalDirection);
// compute this dot product only once
vec3 ambientLighting = vec3(gl_LightModel.ambient)
* vec3(_Color);
vec3 diffuseReflection = attenuation * vec3(_LightColor0)
* vec3(_Color) * max(0.0, dotLN);
vec3 specularReflection;
if (dotLN < 0.0) // light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
float dotHN = dot(halfwayVector, normalDirection);
float dotVN = dot(viewDirection, normalDirection);
float dotHTAlphaX =
dot(halfwayVector, tangentDirection) / _AlphaX;
float dotHBAlphaY = dot(halfwayVector,
binormalDirection) / _AlphaY;
specularReflection = attenuation * vec3(_SpecColor)
* sqrt(max(0.0, dotLN / dotVN))
* exp(-2.0 * (dotHTAlphaX * dotHTAlphaX
+ dotHBAlphaY * dotHBAlphaY) / (1.0 + dotHN));
}
gl_FragColor = vec4(ambientLighting
+ diffuseReflection + specularReflection, 1.0);
}
#endif
Note the term sqrt(max(0, dotLN / dotVN)) which resulted from multiplied with . This makes sure that everything is greater than 0.
Complete Shader Code
[edit | edit source]The complete shader code just defines the appropriate properties and the tangent attribute. Also, it requires a second pass with additive blending but without ambient lighting for additional light sources.
Shader "GLSL anisotropic per-pixel lighting" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_AlphaX ("Roughness in Brush Direction", Float) = 1.0
_AlphaY ("Roughness orthogonal to Brush Direction", Float) = 1.0
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _AlphaX;
uniform float _AlphaY;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
varying vec3 varyingTangentDirection;
// brush direction in world space
#ifdef VERTEX
attribute vec4 Tangent; // tangent vector provided
// by Unity (used as brush direction)
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
varyingTangentDirection = normalize(vec3(
modelMatrix * vec4(vec3(Tangent), 0.0)));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 tangentDirection = normalize(varyingTangentDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 halfwayVector =
normalize(lightDirection + viewDirection);
vec3 binormalDirection =
cross(normalDirection, tangentDirection);
float dotLN = dot(lightDirection, normalDirection);
// compute this dot product only once
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection = attenuation * vec3(_LightColor0)
* vec3(_Color) * max(0.0, dotLN);
vec3 specularReflection;
if (dotLN < 0.0) // light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
float dotHN = dot(halfwayVector, normalDirection);
float dotVN = dot(viewDirection, normalDirection);
float dotHTAlphaX =
dot(halfwayVector, tangentDirection) / _AlphaX;
float dotHBAlphaY =
dot(halfwayVector, binormalDirection) / _AlphaY;
specularReflection = attenuation * vec3(_SpecColor)
* sqrt(max(0.0, dotLN / dotVN))
* exp(-2.0 * (dotHTAlphaX * dotHTAlphaX
+ dotHBAlphaY * dotHBAlphaY) / (1.0 + dotHN));
}
gl_FragColor = vec4(ambientLighting
+ diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _AlphaX;
uniform float _AlphaY;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
varying vec3 varyingTangentDirection;
// brush direction in world space
#ifdef VERTEX
attribute vec4 Tangent; // tangent vector provided
// by Unity (used as brush direction)
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
varyingTangentDirection = normalize(vec3(
modelMatrix * vec4(vec3(Tangent), 0.0)));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 tangentDirection = normalize(varyingTangentDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 halfwayVector =
normalize(lightDirection + viewDirection);
vec3 binormalDirection =
cross(normalDirection, tangentDirection);
float dotLN = dot(lightDirection, normalDirection);
// compute this dot product only once
vec3 diffuseReflection = attenuation * vec3(_LightColor0)
* vec3(_Color) * max(0.0, dotLN);
vec3 specularReflection;
if (dotLN < 0.0) // light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
float dotHN = dot(halfwayVector, normalDirection);
float dotVN = dot(viewDirection, normalDirection);
float dotHTAlphaX =
dot(halfwayVector, tangentDirection) / _AlphaX;
float dotHBAlphaY =
dot(halfwayVector, binormalDirection) / _AlphaY;
specularReflection = attenuation * vec3(_SpecColor)
* sqrt(max(0.0, dotLN / dotVN))
* exp(-2.0 * (dotHTAlphaX * dotHTAlphaX
+ dotHBAlphaY * dotHBAlphaY) / (1.0 + dotHN));
}
gl_FragColor =
vec4(diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Summary
[edit | edit source]Congratulations, you finished a rather advanced tutorial! We have seen:
- What a BRDF (bidirectional reflectance distribution function) is.
- What Ward's BRDF model for anisotropic reflection is.
- How to implement Ward's BRDF model.
Further Reading
[edit | edit source]If you still want to know more
- about lighting with the Phong reflection model, you should read Section “Specular Highlights”.
- about per-pixel lighting (i.e. Phong shading), you should read Section “Smooth Specular Highlights”.
- about Ward's BRDF model, you should read his article “Measuring and Modeling Anisotropic Reflection”, Computer Graphics (SIGGRAPH ’92 Proceedings), pp. 265–272, July 1992. (A copy of the paper is available online.) Or you could read Section 14.3 of the book “OpenGL Shading Language” (3rd edition) by Randi Rost and others, published 2009 by Addison-Wesley, or Section 8 in the Lighting chapter of the book “Programming Vertex, Geometry, and Pixel Shaders” (2nd edition, 2008) by Wolfgang Engel, Jack Hoxley, Ralf Kornmann, Niko Suni, and Jason Zink (which is available online.)
Specular Highlights at Silhouettes
[edit | edit source]
This tutorial covers the Fresnel factor for specular highlights.
It is one of several tutorials about lighting that go beyond the Phong reflection model. However, it is based on lighting with the Phong reflection model as described in Section “Specular Highlights” (for per-vertex lighting) and Section “Smooth Specular Highlights” (for per-pixel lighting). If you haven't read those tutorials yet, you should read them first.
Many materials (e.g. matte paper) show strong specular reflection when light grazes the surface; i.e., when backlight is reflected from the opposite direction to the viewer as in the photo to the left. The Fresnel factor explains this strong reflection for some materials. Of course, there are also other reasons for bright silhouettes, e.g. translucent hair or fabrics (see Section “Translucent Surfaces”).
Interestingly, the effect is often hardly visible because it is most likely when the background of the silhouette is very bright. In this case, however, a bright silhouette will just blend into the background and thus become hardly noticeable.

Schlick's Approximation of the Fresnel Factor
[edit | edit source]The Fresnel factor describes the specular reflectance of nonconducting materials for unpolarized light of wavelength . Schlick's approximation is:
where V is the normalized direction to the viewer and H is the normalized halfway vector: H = (V + L) / |V + L| with L being the normalized direction to the light source. is the reflectance for H·V = 1, i.e. when the direction to the light source, the direction to the viewer, and the halfway vector are all identical. On the other hand, becomes 1 for H·V = 0, i.e. when the halfway vector is orthogonal to the direction to the viewer, which means that the direction to the light source is opposite to the direction to the viewer (i.e. the case of a grazing light reflection). In fact, is independent of the wavelength in this case and the material behaves just like a perfect mirror.
Using the built-in GLSL function mix(x,y,w) = x*(1-w) + y*w we can rewrite Schlick's approximation as:
which might be slightly more efficient, at least on some GPUs. We will take the dependency on the wavelength into account by allowing for different values of for each color component; i.e. we consider it an RGB vector. In fact, we identify it with the constant material color from Section “Specular Highlights”. In other words, the Fresnel factor adds a dependency of the material color on the angle between the direction to the viewer and the halfway vector. Thus, we replace the constant material color with Schlick's approximation (using ) in any calculation of the specular reflection.
For example, our equation for the specular term in the Phong reflection model was (see Section “Specular Highlights”):
Replacing by Schlick's approximation for the Fresnel factor with yields:
Implementation
[edit | edit source]The implementation is based on the shader code from Section “Smooth Specular Highlights”. It just computes the halfway vector and includes the approximation of the Fresnel factor:
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
vec3 halfwayDirection =
normalize(lightDirection + viewDirection);
float w = pow(1.0 - max(0.0,
dot(halfwayDirection, viewDirection)), 5.0);
specularReflection = attenuation * vec3(_LightColor0)
* mix(vec3(_SpecColor), vec3(1.0), w)
* pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
Complete Shader Code
[edit | edit source]Putting the code snippet from above in the complete shader from Section “Smooth Specular Highlights” results in this shader:
Shader "GLSL Fresnel highlights" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
vec3 halfwayDirection =
normalize(lightDirection + viewDirection);
float w = pow(1.0 - max(0.0,
dot(halfwayDirection, viewDirection)), 5.0);
specularReflection = attenuation * vec3(_LightColor0)
* mix(vec3(_SpecColor), vec3(1.0), w)
* pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(ambientLighting
+ diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
vec3 halfwayDirection =
normalize(lightDirection + viewDirection);
float w = pow(1.0 - max(0.0,
dot(halfwayDirection, viewDirection)), 5.0);
specularReflection = attenuation * vec3(_LightColor0)
* mix(vec3(_SpecColor), vec3(1.0), w)
* pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor =
vec4(diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Artistic Control
[edit | edit source]A useful modification of the implementation above is to replace the power 5.0 by a user-specified shader property. This would give CG artists the option to exaggerate or attenuate the effect of the Fresnel factor depending on their artistic needs.
Consequences for Semitransparent Surfaces
[edit | edit source]Apart from influencing specular highlights, a Fresnel factor should also influence the opacity of semitransparent surfaces. In fact, the Fresnel factor describes how a surface becomes more reflective for grazing light rays, which implies that less light is absorbed, refracted, or transmitted, i.e. the transparency decreases and therefore the opacity increases. To this end, a Fresnel factor could be computed with the surface normal vector N instead of the halfway vector H and the opacity of a semitransparent surface could increase from a user-specified value (for viewing in the direction of the surface normal) to 1 (independently of the wavelength) with
.
In Section “Silhouette Enhancement” the opacity was considered to result from an attenuation of light as it passes through a layer of semitransparent material. This opacity should be combined with the opacity due to increased reflectivity in the following way: the total opacity is 1 minus the total transparency which is the product of the transparency due to attenuation (which is 1 minus ) and the transparency due to the Fresnel factor (which is 1 minus ), i.e.:
is the opacity as computed above while is the opacity as computed in Section “Silhouette Enhancement”. For the view direction parallel to the surface normal vector, and could be specified by the user. Then the equation fixes for the normal direction and, in fact, it fixes all constants and therefore can be computed for all view directions. Note that neither the diffuse reflection nor the specular reflection should be multiplied with the opacity since the specular reflection is already multiplied with the Fresnel factor and the diffuse reflection should only be multiplied with the opacity due to attenuation .
Summary
[edit | edit source]Congratulations, you finished one of the somewhat advanced tutorials! We have seen:
- What the Fresnel factor is.
- What Schlick's approximation to the Fresnel factor is.
- How to implement Schlick's approximation for specular highlights.
- How to add more artistic control to the implementation.
- How to use the Fresnel factor for semitransparent surfaces.
Further Reading
[edit | edit source]If you still want to know more
- about lighting with the Phong reflection model, you should read Section “Specular Highlights”.
- about per-pixel lighting (i.e. Phong shading), you should read Section “Smooth Specular Highlights”.
- about Schlick's approximation, you should read his article “An inexpensive BRDF model for physically-based rendering” by Christophe Schlick, Computer Graphics Forum, 13(3):233—246, 1994. or you could read Section 14.1 of the book “OpenGL Shading Language” (3rd edition) by Randi Rost and others, published 2009 by Addison-Wesley, or Section 5 in the Lighting chapter of the book “Programming Vertex, Geometry, and Pixel Shaders” (2nd edition, 2008) by Wolfgang Engel, Jack Hoxley, Ralf Kornmann, Niko Suni, and Jason Zink (which is available online.)
Diffuse Reflection of Skylight
[edit | edit source]
This tutorial covers hemisphere lighting.
It is based on diffuse per-vertex lighting as described in Section “Diffuse Reflection”. If you haven't read that tutorial yet, you should read it first.
Hemisphere lighting basically computes diffuse illumination with a huge light source that covers a whole hemisphere around the scene, for example the sky. It often includes the illumination with another hemisphere from below using a different color since the calculation is almost for free. In the photo to the left, the spherical building is illuminated by a overcast sky. However, there is also illumination by the green water basin around it, which results in a noticeable greenish illumination of the lower half of the building.

Hemisphere Lighting
[edit | edit source]If we assume that each point (in direction L) of a hemisphere around a point on the surface acts as a light source, then we should integrate the diffuse illumination (given by max(0, L·N) as discussed in Section “Diffuse Reflection”) from all the points on the hemisphere by an integral. Let's call the normalized direction of the rotation axis of the hemisphere U (for “up”). If the surface normal N points in the direction of U, we have full illumination with a color specified by the user. If there is an angle γ between them (i.e. cos(γ) = U·N), only a spherical wedge (see the Wikipedia article) of the hemisphere illuminates the surface point. The fraction w of this illumination in comparison to the full illumination is:
Thus, we can compute the incoming light as w times the user-specified color of the full illumination by the hemisphere. The hemisphere in the opposite direction will illuminate the surface point with 1-w times another color (which might be black if we don't need it). The next section explains how to derive this equation for w.
Derivation of the Equation
[edit | edit source]For anyone interested (and because I didn't find it on the web) here is a derivation of the equation for w. We integrate the illumination over the hemisphere at distance 1 in a spherical coordinate system attached to the surface point with the direction of N in the direction of the y axis. If N and U point in the same direction, the integral is (apart from a constant color specified by the user):
The term sin(θ) is the Jacobian determinant for our integration on the surface of a sphere of radius 1, (x, y, z) is (cos(φ)sin(θ), sin(φ)sin(θ), cos(θ)), and N = (0,1,0). Thus, the integral becomes:
The constant π will be included in the user-defined color of the maximum illumination. If there is an angle γ with cos(γ) = U·N between N and U, then the integration is only over a spherical wedge (from γ to π):
Shader Code
[edit | edit source]The implementation is based on the code from Section “Diffuse Reflection”. In a more elaborated implementation, the contributions of other light sources would also be included, for example using the Phong reflection model as discussed in Section “Specular Highlights”. In that case, hemisphere lighting would be included in the same way as ambient lighting.
Here, however, the only illumination is due to hemisphere lighting. The equation for w is:
We implement it in world space, i.e. we have to transform the surface normal vector N to world space (see Section “Shading in World Space”), while U is specified in world space by the user. We normalize the vectors and compute w before using w and 1-w to compute the illumination based on the user-specified colors. Actually, it is pretty straightforward.
Shader "GLSL per-vertex hemisphere lighting" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_UpperHemisphereColor ("Upper Hemisphere Color", Color)
= (1,1,1,1)
_LowerHemisphereColor ("Lower Hemisphere Color", Color)
= (1,1,1,1)
_UpVector ("Up Vector", Vector) = (0,1,0,0)
}
SubShader {
Pass {
GLSLPROGRAM
// shader properties specified by users
uniform vec4 _Color;
uniform vec4 _UpperHemisphereColor;
uniform vec4 _LowerHemisphereColor;
uniform vec3 _UpVector;
// The following built-in uniforms
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
varying vec4 color;
// the hemisphere lighting computed in the vertex shader
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
vec3 normalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
vec3 upDirection = normalize(_UpVector);
float w = 0.5 * (1.0 + dot(upDirection, normalDirection));
color = (w * _UpperHemisphereColor
+ (1.0 - w) * _LowerHemisphereColor) * _Color;
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = color;
}
#endif
ENDGLSL
}
}
}
Summary
[edit | edit source]Congratulations, you have finished another tutorial! We have seen:
- What hemisphere lighting is.
- What the equation for hemisphere lighting is.
- How to implement hemisphere lighting.
Further Reading
[edit | edit source]If you still want to know more
- about lighting with the diffuse reflection, you should read Section “Diffuse Reflection”.
- about hemisphere lighting, you could read Section 12.1 of the book “OpenGL Shading Language” (3rd edition) by Randi Rost et al., published 2009 by Addison-Wesley.
Translucent Surfaces
[edit | edit source]
This tutorial covers translucent surfaces.
It is one of several tutorials about lighting that go beyond the Phong reflection model. However, it is based on per-pixel lighting with the Phong reflection model as described in Section “Smooth Specular Highlights”. If you haven't read that tutorial yet, you should read it first.
The Phong reflection model doesn't take translucency into account, i.e. the possibility that light is transmitted through a material. This tutorial is about translucent surfaces, i.e. surfaces that allow light to transmit from one face to the other, e.g. paper, clothes, plastic films, or leaves.

Diffuse Translucency
[edit | edit source]We will distinguish between two kinds of light transmission: diffuse translucency and forward-scattered translucency, which correspond to the diffuse and specular terms in the Phong reflection model. Diffuse translucency is a diffuse transmission of light analogously to the diffuse reflection term in the Phong reflection model (see Section “Diffuse Reflection”): it only depends on the dot product of the surface normal vector and the direction to the light source — except that we use the negative surface normal vector since the light source is on the backside, thus the equation for the diffuse translucent illumination is:
This is the most common illumination for many translucent surfaces, e.g. paper and leaves.
Forward-Scattered Translucency
[edit | edit source]Some translucent surfaces (e.g. plastic films) are almost transparent and allow light to shine through the surface almost directly but with some forward scattering; i.e., one can see light sources through the surface but the image is somewhat blurred. This is similar to the specular term of the Phong reflection model (see Section “Specular Highlights” for the equation) except that we replace the reflected light direction R by the negative light direction -L and the exponent corresponds now to the sharpness of the forward-scattered light:
Of course, this model of forward-scattered translucency is not accurate at all but it allows us to fake the effect and tweak the parameters.
Implementation
[edit | edit source]The following implementation is based on Section “Smooth Specular Highlights”, which presents per-pixel lighting with the Phong reflection model. The implementation allows for rendering backfaces and flips the surface normal vector in this case. A more elaborated version could also use different colors for the frontface and the backface (see Section “Two-Sided Smooth Surfaces”). In addition to the terms of the Phong reflection model, we also compute illumination by diffuse translucency and forward-scattered translucency. Here is the part that is specific for the fragment shader:
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
if (!gl_FrontFacing) // do we look at the backface?
{
normalDirection = -normalDirection; // flip normal
}
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
// Computation of the Phong reflection model:
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
// Computation of the translucent illumination:
vec3 diffuseTranslucency = attenuation * vec3(_LightColor0)
* vec3(_DiffuseTranslucentColor)
* max(0.0, dot(lightDirection, -normalDirection));
vec3 forwardTranslucency;
if (dot(normalDirection, lightDirection) > 0.0)
// light source on the wrong side?
{
forwardTranslucency = vec3(0.0, 0.0, 0.0);
// no forward-scattered translucency
}
else // light source on the right side
{
forwardTranslucency = attenuation * vec3(_LightColor0)
* vec3(_ForwardTranslucentColor) * pow(max(0.0,
dot(-lightDirection, viewDirection)), _Sharpness);
}
// Computation of the complete illumination:
gl_FragColor = vec4(ambientLighting
+ diffuseReflection + specularReflection
+ diffuseTranslucency + forwardTranslucency, 1.0);
}
#endif
Complete Shader Code
[edit | edit source]The complete shader code defines the shader properties for the material constants and adds another pass for additional light sources with additive blending but without the ambient lighting:
Shader "GLSL translucent surfaces" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
_DiffuseTranslucentColor ("Diffuse Translucent Color", Color)
= (1,1,1,1)
_ForwardTranslucentColor ("Forward Translucent Color", Color)
= (1,1,1,1)
_Sharpness ("Sharpness", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
Cull Off // show frontfaces and backfaces
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _DiffuseTranslucentColor;
uniform vec4 _ForwardTranslucentColor;
uniform float _Sharpness;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
if (!gl_FrontFacing) // do we look at the backface?
{
normalDirection = -normalDirection; // flip normal
}
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
vec3 diffuseTranslucency = attenuation * vec3(_LightColor0)
* vec3(_DiffuseTranslucentColor)
* max(0.0, dot(lightDirection, -normalDirection));
vec3 forwardTranslucency;
if (dot(normalDirection, lightDirection) > 0.0)
// light source on the wrong side?
{
forwardTranslucency = vec3(0.0, 0.0, 0.0);
// no forward-scattered translucency
}
else // light source on the right side
{
forwardTranslucency = attenuation * vec3(_LightColor0)
* vec3(_ForwardTranslucentColor) * pow(max(0.0,
dot(-lightDirection, viewDirection)), _Sharpness);
}
gl_FragColor = vec4(ambientLighting
+ diffuseReflection + specularReflection
+ diffuseTranslucency + forwardTranslucency, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Cull Off
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _DiffuseTranslucentColor;
uniform vec4 _ForwardTranslucentColor;
uniform float _Sharpness;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
if (!gl_FrontFacing) // do we look at the backface?
{
normalDirection = -normalDirection; // flip normal
}
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
vec3 diffuseTranslucency = attenuation * vec3(_LightColor0)
* vec3(_DiffuseTranslucentColor)
* max(0.0, dot(lightDirection, -normalDirection));
vec3 forwardTranslucency;
if (dot(normalDirection, lightDirection) > 0.0)
// light source on the wrong side?
{
forwardTranslucency = vec3(0.0, 0.0, 0.0);
// no forward-scattered translucency
}
else // light source on the right side
{
forwardTranslucency = attenuation * vec3(_LightColor0)
* vec3(_ForwardTranslucentColor) * pow(max(0.0,
dot(-lightDirection, viewDirection)), _Sharpness);
}
gl_FragColor = vec4(diffuseReflection + specularReflection
+ diffuseTranslucency + forwardTranslucency, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Summary
[edit | edit source]Congratulations! You finished this tutorial on translucent surfaces, which are very common but cannot be modeled by the Phong reflection model. We have covered:
- What translucent surfaces are.
- Which forms of translucency are most common (diffuse translucency and forward-scattered translucency).
- How to implement diffuse and forward-scattered translucency.
Further Reading
[edit | edit source]If you still want to know more
- about the diffuse term of the Phong reflection model, you should read Section “Diffuse Reflection”.
- about the ambient or the specular term of the Phong reflection model, you should read Section “Specular Highlights”.
- about per-pixel lighting with the Phong reflection model, you should read Section “Smooth Specular Highlights”.
- about per-pixel lighting of two-sided surfaces, you should read Section “Two-Sided Smooth Surfaces”.
Translucent Bodies
[edit | edit source]
This tutorial covers translucent bodies.
It is one of several tutorials about lighting that go beyond the Phong reflection model. However, it is based on per-pixel lighting with the Phong reflection model as described in Section “Smooth Specular Highlights”. If you haven't read that tutorial yet, you should read it first.
The Phong reflection model doesn't take translucency into account, i.e. the possibility that light is transmitted through a material. While Section “Translucent Surfaces” handled translucent surfaces, this tutorial handles the case of three-dimensional bodies instead of thin surfaces. Examples of translucent materials are wax, jade, marble, skin, etc.

Waxiness
[edit | edit source]Unfortunately, the light transport in translucent bodies (i.e. subsurface scattering) is quite challenging in a real-time game engine. Rendering a depth map from the point of view of the light source would help, but since this tutorial is restricted to the free version of Unity, this approach is out of the question. Therefore, we will fake some of the effects of subsurface scattering.
The first effect will be called “waxiness” and describes the smooth, lustrous appearance of wax which lacks the hard contrasts that diffuse reflection can provide. Ideally, we would like to smooth the surface normals before we compute the diffuse reflection (but not the specular reflection) and, in fact, this is possible if a normal map is used. Here, however, we take another approach. In order to soften the hard contrasts of diffuse reflection, which is caused by the term max(0, N·L) (see Section “Diffuse Reflection”), we reduce the influence of this term as the waxiness increases from 0 to 1. More specifically, we multiply the term max(0, N·L) with . However, this will not only reduce the contrast but also the overall brightness of the illumination. To avoid this, we add the waxiness to fake the additional light due to subsurface scattering, which is stronger the “waxier” a material is.
Thus, instead of this equation for diffuse reflection:
we get:
with the waxiness between 0 (i.e. regular diffuse reflection) and 1 (i.e. no dependency on N·L).
This approach is easy to implement, easy to compute for the GPU, easy to control, and it does resemble the appearance of wax and jade, in particular if combined with specular highlights with a high shininess.

Transmittance of Backlight
[edit | edit source]The second effect that we are going to fake is backlight that passes through a body and exits at the visible front of the body. This effect is the stronger, the smaller the distance between the back and the front, i.e. in particular at silhouettes, where the distance between the back and the front actually becomes zero. We could, therefore, use the techniques discussed in Section “Silhouette Enhancement” to generate more illumination at the silhouettes. However, the effect becomes somewhat more convincing if we take the actual diffuse illumination at the back of a closed mesh into account. To this end, we proceed as follows:
- We render only back faces and compute the diffuse reflection weighted with a factor that describes how close the point (on the back) is to a silhouette. We mark the pixels with an opacity of 0. (Usually, pixels in the framebuffer have opacity 1. The technique of marking pixels by setting their opacity to 0 is also used and explained in more detail in Section “Mirrors”.)
- We render only front faces (in black) and set the color of all pixels that have opacity 1 to black (i.e. all pixels that we haven't rasterized in the first step). This is necessary in case another object intersects with the mesh.
- We render front faces again with the illumination from the front and add the color in the framebuffer multiplied with a factor that describes how close the point (on the front) is to a silhouette.
In the first and third step, we use the silhouette factor 1 - |N·L|, which is 1 at a silhouette and 0 if the viewer looks straight onto the surface. (An exponent for the dot product could be introduced to allow for more artistic control.) Thus, all the calculations are actually rather straightforward. The complicated part is the blending.
Implementation
[edit | edit source]The implementation relies heavily on blending, which is discussed in Section “Transparency”. In addition to three passes corresponding to the steps mentioned above, we also need two more additional passes for additional light sources on the back and the front. With so many passes, it makes sense to get a clear idea of what the render passes are supposed to do. To this end, a skeleton of the shader without the GLSL code is very helpful:
Shader "GLSL translucent bodies" {
Properties {
_Color ("Diffuse Color", Color) = (1,1,1,1)
_Waxiness ("Waxiness", Range(0,1)) = 0
_SpecColor ("Specular Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
_TranslucentColor ("Translucent Color", Color) = (0,0,0,1)
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" } // pass for
// ambient light and first light source on back faces
Cull Front // render back faces only
Blend One Zero // mark rasterized pixels in framebuffer
// with alpha = 0 (usually they should have alpha = 1)
GLSLPROGRAM
[...]
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources on back faces
Cull Front // render back faces only
Blend One One // additive blending
GLSLPROGRAM
[...]
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardBase" } // pass for
// setting pixels that were not rasterized to black
Cull Back // render front faces only (default behavior)
Blend Zero OneMinusDstAlpha // set colors of pixels
// with alpha = 1 to black by multiplying with 1-alpha
GLSLPROGRAM
#ifdef VERTEX
void main() {
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main() { gl_FragColor = vec4(0.0); }
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardBase" } // pass for
// ambient light and first light source on front faces
Cull Back // render front faces only
Blend One SrcAlpha // multiply color in framebuffer
// with silhouetteness in fragment's alpha and add colors
GLSLPROGRAM
[...]
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources on front faces
Cull Back // render front faces only
Blend One One // additive blending
GLSLPROGRAM
[...]
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
This skeleton is already quite long; however, it gives a good idea of how the overall shader is organized.
Complete Shader Code
[edit | edit source]In the following complete shader code, note that the property _TranslucentColor instead of _Color is used in the computation of the diffuse and ambient part on the back faces. Also note how the “silhouetteness” is computed on the back faces as well as on the front faces; however, it is directly multiplied only to the fragment color of the back faces. On the front faces, it is only indirectly multiplied through the alpha component of the fragment color and blending of this alpha with the destination color (the color of pixels in the framebuffer). Finally, the “waxiness” is only used for the diffuse reflection on the front faces.
Shader "GLSL translucent bodies" {
Properties {
_Color ("Diffuse Color", Color) = (1,1,1,1)
_Waxiness ("Waxiness", Range(0,1)) = 0
_SpecColor ("Specular Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
_TranslucentColor ("Translucent Color", Color) = (0,0,0,1)
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" } // pass for
// ambient light and first light source on back faces
Cull Front // render back faces only
Blend One Zero // mark rasterized pixels in framebuffer
// with alpha = 0 (usually they should have alpha = 1)
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform float _Waxiness;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _TranslucentColor;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_TranslucentColor);
vec3 diffuseReflection = attenuation
* vec3(_LightColor0) * vec3(_TranslucentColor)
* max(0.0, dot(normalDirection, lightDirection));
float silhouetteness =
1.0 - abs(dot(viewDirection, normalDirection));
gl_FragColor = vec4(silhouetteness
* (ambientLighting + diffuseReflection), 0.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources on back faces
Cull Front // render back faces only
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform float _Waxiness;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _TranslucentColor;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection = attenuation
* vec3(_LightColor0) * vec3(_TranslucentColor)
* max(0.0, dot(normalDirection, lightDirection));
float silhouetteness =
1.0 - abs(dot(viewDirection, normalDirection));
gl_FragColor =
vec4(silhouetteness * diffuseReflection, 0.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardBase" } // pass for
// setting pixels that were not rasterized to black
Cull Back // render front faces only (default behavior)
Blend Zero OneMinusDstAlpha // set colors of pixels
// with alpha = 1 to black by multiplying with 1-alpha
GLSLPROGRAM
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(0.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardBase" } // pass for
// ambient light and first light source on front faces
Cull Back // render front faces only
Blend One SrcAlpha // multiply color in framebuffer
// with silhouetteness in fragment's alpha and add colors
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform float _Waxiness;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _TranslucentColor;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* (_Waxiness + (1.0 - _Waxiness)
* max(0.0, dot(normalDirection, lightDirection)));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
float silhouetteness =
1.0 - abs(dot(viewDirection, normalDirection));
gl_FragColor = vec4(ambientLighting + diffuseReflection
+ specularReflection, silhouetteness);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources on front faces
Cull Back // render front faces only
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform float _Waxiness;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _TranslucentColor;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* (_Waxiness + (1.0 - _Waxiness)
* max(0.0, dot(normalDirection, lightDirection)));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor =
vec4(diffuseReflection + specularReflection, 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Summary
[edit | edit source]Congratulations! You finished this tutorial on translucent bodies, which was mainly about:
- How to fake the appearance of wax.
- How to fake the appearance of silhouettes of translucent materials lit by backlight.
- How to implement these techniques.
Further Reading
[edit | edit source]If you still want to know more
- about translucent surfaces, you should read Section “Translucent Surfaces”.
- about the diffuse term of the Phong reflection model, you should read Section “Diffuse Reflection”.
- about the ambient or the specular term of the Phong reflection model, you should read Section “Specular Highlights”.
- about per-pixel lighting with the Phong reflection model, you should read Section “Smooth Specular Highlights”.
- about basic real-time techniques for subsurface scattering, you could read Chapter 16, “Real-Time Approximations to Subsurface Scattering” by Simon Green of the book “GPU Gems” by Randima Fernando (editor) published 2004 by Addison-Wesley, which is available online.
Soft Shadows of Spheres
[edit | edit source]
This tutorial covers soft shadows of spheres.
It is one of several tutorials about lighting that go beyond the Phong reflection model, which is a local illumination model and therefore doesn't take shadows into account. The presented technique renders the soft shadow of a single sphere on any mesh and is somewhat related to a technique that was proposed by Orion Sky Lawlor (see the “Further Reading” section). The shader can be extended to render the shadows of a small number of spheres at the cost of rendering performance; however, it cannot easily be applied to any other kind of shadow caster. Potential applications are computer ball games (where the ball is often the only object that requires a soft shadow and the only object that should cast a dynamic shadow on all other objects), computer games with a spherical main character (e.g. “Marble Madness”), visualizations that consist only of spheres (e.g. planetary visualizations, ball models of small nuclei, atoms, or molecules, etc.), or test scenes that can be populated with spheres and benefit from soft shadows.
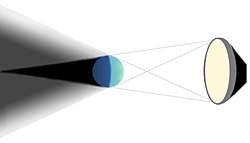

Soft Shadows
[edit | edit source]While directional light sources and point light sources produce hard shadows, any area light source generates a soft shadow. This is also true for all real light sources, in particular the sun and any light bulb or lamp. From some points behind the shadow caster, no part of the light source is visible and the shadow is uniformly dark: this is the umbra. From other points, more or less of the light source is visible and the shadow is therefore less or more complete: this is the penumbra. Finally, there are points from where the whole area of the light source is visible: these points are outside of the shadow.
In many cases, the softness of a shadow depends mainly on the distance between the shadow caster and the shadow receiver: the larger the distance, the softer the shadow. This is a well known effect in art; see for example the painting by Caravaggio to the right.

Computation
[edit | edit source]We are going to approximately compute the shadow of a point on a surface when a sphere of radius at S (relative to the surface point) is occluding a spherical light source of radius at L (again relative to the surface point); see the figure to the left.
To this end, we consider a tangent in direction T to the sphere and passing through the surface point. Furthermore, this tangent is chosen to be in the plane spanned by L and S, i.e. parallel to the view plane of the figure to the left. The crucial observation is that the minimum distance of the center of the light source and this tangent line is directly related to the amount of shadowing of the surface point because it determines how large the area of the light source is that is visible from the surface point. More precisely spoken, we require a signed distance (positive if the tangent is on the same side of L as the sphere, negative otherwise) to determine whether the surface point is in the umbra (), in the penumbra (), or outside of the shadow ().
For the computation of , we consider the angles between L and S and between T and S. The difference between these two angles is the angle between L and T, which is related to by:
.
Thus, so far we have:
We can compute the angle between T and S using
.
Thus:
.
For the angle between L and S we use a feature of the cross product:
.
Therefore:
.
All in all we have:
The approximation we did so far, doesn't matter much; more importantly it doesn't produce rendering artifacts. If performance is an issue one could go further and use arcsin(x) ≈ x; i.e., one could use:
This avoids all trigonometric functions; however, it does introduce rendering artifacts (in particular if a specular highlight is in the penumbra that is facing the light source). Whether these rendering artifacts are worth the gains in performance has to be decided for each case.
Next we look at how to compute the level of shadowing based on . As decreases from to , should increase from 0 to 1. In other words, we want a smooth step from 0 to 1 between values -1 and 1 of . Probably the most efficient way to achieve this is to use the Hermite interpolation offered by the built-in GLSL function smoothstep(a,b,x) = t*t*(3-2*t) with t=clamp((x-a)/(b-a),0,1):
While this isn't a particular good approximation of a physically-based relation between and , it still gets the essential features right.
Furthermore, should be 0 if the light direction L is in the opposite direction of S; i.e., if their dot product is negative. This condition turns out to be a bit tricky since it leads to a noticeable discontinuity on the plane where L and S are orthogonal. To soften this discontinuity, we can again use smoothstep to compute an improved value :
Additionally, we have to set to 0 if a point light source is closer to the surface point than the occluding sphere. This is also somewhat tricky because the spherical light source can intersect the shadow-casting sphere. One solution that avoids too obvious artifacts (but fails to deal with the full intersection problem) is:
In the case of a directional light source we just set . Then the term , which specifies the level of unshadowed lighting, should be multiplied to any illumination by the light source. (Thus, ambient light shouldn't be multiplied with this factor.) If the shadows of multiple shadow casters are computed, the terms for all shadow casters have to be combined for each light source. The common way is to multiply them although this can be inaccurate (in particular if the umbras overlap).
Implementation
[edit | edit source]The implementation computes the length of the lightDirection and sphereDirection vectors and then proceeds with the normalized vectors. This way, the lengths of these vectors have to be computed only once and we even avoid some divisions because we can use normalized vectors. Here is the crucial part of the fragment shader:
// computation of level of shadowing w
vec3 sphereDirection = vec3(_SpherePosition - position);
float sphereDistance = length(sphereDirection);
sphereDirection = sphereDirection / sphereDistance;
float d = lightDistance
* (asin(min(1.0,
length(cross(lightDirection, sphereDirection))))
- asin(min(1.0, _SphereRadius / sphereDistance)));
float w = smoothstep(-1.0, 1.0, -d / _LightSourceRadius);
w = w * smoothstep(0.0, 0.2,
dot(lightDirection, sphereDirection));
if (0.0 != _WorldSpaceLightPos0.w) // point light source?
{
w = w * smoothstep(0.0, _SphereRadius,
lightDistance - sphereDistance);
}
The use of asin(min(1.0, ...)) makes sure that the argument of asin is in the allowed range.
Complete Shader Code
[edit | edit source]The complete source code defines properties for the shadow-casting sphere and the light source radius. All values are expected to be in world coordinates. For directional light sources, the light source radius should be given in radians (1 rad = 180° / π). The best way to set the position and radius of the shadow-casting sphere is a short script that should be attached to all shadow-receiving objects that use the shader, for example:
@script ExecuteInEditMode()
var occluder : GameObject;
function Update () {
if (null != occluder) {
renderer.sharedMaterial.SetVector("_SpherePosition",
occluder.transform.position);
renderer.sharedMaterial.SetFloat("_SphereRadius",
occluder.transform.localScale.x / 2.0);
}
}
This script has a public variable occluder that should be set to the shadow-casting sphere. Then it sets the properties _SpherePostion and _SphereRadius of the following shader (which should be attached to the same shadow-receiving object as the script).
Shader "GLSL shadow of sphere" {
Properties {
_Color ("Diffuse Material Color", Color) = (1,1,1,1)
_SpecColor ("Specular Material Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
_SpherePosition ("Sphere Position", Vector) = (0,0,0,1)
_SphereRadius ("Sphere Radius", Float) = 1
_LightSourceRadius ("Light Source Radius", Float) = 0.005
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _SpherePosition;
// center of shadow-casting sphere in world coordinates
uniform float _SphereRadius;
// radius of shadow-casting sphere
uniform float _LightSourceRadius;
// in radians for directional light sources
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float lightDistance;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
lightDistance = 1.0;
}
else // point or spot light
{
lightDirection = vec3(_WorldSpaceLightPos0 - position);
lightDistance = length(lightDirection);
attenuation = 1.0 / lightDistance; // linear attenuation
lightDirection = lightDirection / lightDistance;
}
// computation of level of shadowing w
vec3 sphereDirection = vec3(_SpherePosition - position);
float sphereDistance = length(sphereDirection);
sphereDirection = sphereDirection / sphereDistance;
float d = lightDistance
* (asin(min(1.0,
length(cross(lightDirection, sphereDirection))))
- asin(min(1.0, _SphereRadius / sphereDistance)));
float w = smoothstep(-1.0, 1.0, -d / _LightSourceRadius);
w = w * smoothstep(0.0, 0.2,
dot(lightDirection, sphereDirection));
if (0.0 != _WorldSpaceLightPos0.w) // point light source?
{
w = w * smoothstep(0.0, _SphereRadius,
lightDistance - sphereDistance);
}
vec3 ambientLighting =
vec3(gl_LightModel.ambient) * vec3(_Color);
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4(ambientLighting
+ (1.0 - w) * (diffuseReflection + specularReflection),
1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend One One // additive blending
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _SpecColor;
uniform float _Shininess;
uniform vec4 _SpherePosition;
// center of shadow-casting sphere in world coordinates
uniform float _SphereRadius;
// radius of shadow-casting sphere
uniform float _LightSourceRadius;
// in radians for directional light sources
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float lightDistance;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
lightDistance = 1.0;
}
else // point or spot light
{
lightDirection = vec3(_WorldSpaceLightPos0 - position);
lightDistance = length(lightDirection);
attenuation = 1.0 / lightDistance; // linear attenuation
lightDirection = lightDirection / lightDistance;
}
// computation of level of shadowing w
vec3 sphereDirection = vec3(_SpherePosition - position);
float sphereDistance = length(sphereDirection);
sphereDirection = sphereDirection / sphereDistance;
float d = lightDistance
* (asin(min(1.0,
length(cross(lightDirection, sphereDirection))))
- asin(min(1.0, _SphereRadius / sphereDistance)));
float w = smoothstep(-1.0, 1.0, -d / _LightSourceRadius);
w = w * smoothstep(0.0, 0.2,
dot(lightDirection, sphereDirection));
if (0.0 != _WorldSpaceLightPos0.w) // point light source?
{
w = w * smoothstep(0.0, _SphereRadius,
lightDistance - sphereDistance);
}
vec3 diffuseReflection =
attenuation * vec3(_LightColor0) * vec3(_Color)
* max(0.0, dot(normalDirection, lightDirection));
vec3 specularReflection;
if (dot(normalDirection, lightDirection) < 0.0)
// light source on the wrong side?
{
specularReflection = vec3(0.0, 0.0, 0.0);
// no specular reflection
}
else // light source on the right side
{
specularReflection = attenuation * vec3(_LightColor0)
* vec3(_SpecColor) * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess);
}
gl_FragColor = vec4((1.0 - w) * (diffuseReflection
+ specularReflection), 1.0);
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
Summary
[edit | edit source]Congratulations! I hope you succeeded to render some nice soft shadows. We have looked at:
- What soft shadows are and what the penumbra and umbra is.
- How to compute soft shadows of spheres.
- How to implement the computation, including a script in JavaScript that sets some properties based on another
GameObject.
Further Reading
[edit | edit source]If you still want to know more
- about the rest of the shader code, you should read Section “Smooth Specular Highlights”.
- about computations of soft shadows, you should read a publication by Orion Sky Lawlor: “Interpolation-Friendly Soft Shadow Maps” in Proceedings of Computer Graphics and Virtual Reality ’06, pages 111–117. A preprint is available online.
Toon Shading
[edit | edit source]
This tutorial covers toon shading (also known as cel shading) as an example of non-photorealistic rendering techniques.
It is one of several tutorials about lighting that go beyond the Phong reflection model. However, it is based on per-pixel lighting with the Phong reflection model as described in Section “Smooth Specular Highlights”. If you haven't read that tutorial yet, you should read it first.
Non-photorealistic rendering is a very broad term in computer graphics that covers all rendering techniques and visual styles that are obviously and deliberately different from the appearance of photographs of physical objects. Examples include hatching, outlining, distortions of linear perspective, coarse dithering, coarse color quantization, etc.
Toon shading (or cel shading) is any subset of non-photorealistic rendering techniques that is used to achieve a cartoonish or hand-drawn appearance of three-dimensional models.

Shaders for a Specific Visual Style
[edit | edit source]John Lasseter from Pixar once said in an interview: “Art challenges technology, and technology inspires the art.” Many visual styles and drawing techniques that are traditionally used to depict three-dimensional objects are in fact very difficult to implement in shaders. However, there is no fundamental reason not to try it.
When implementing one or more shaders for any specific visual style, one should first determine which features of the style have to be implemented. This is mainly a task of precise analysis of examples of the visual style. Without such examples, it is usually unlikely that the characteristic features of a style can be determined. Even artists who master a certain style are unlikely to be able to describe these features appropriately; for example, because they are no longer aware of certain features or might consider some characteristic features as unnecessary imperfections that are not worth mentioning.
For each of the features it should then be determined whether and how accurately to implement them. Some features are rather easy to implement, others are very difficult to implement by a programmer or to compute by a GPU. Therefore, a discussion between shader programmers and (technical) artists in the spirit of John Lasseter's quote above is often extremely worthwhile to decide which features to include and how accurately to reproduce them.

Stylized Specular Highlights
[edit | edit source]In comparison to the Phong reflection model that was implemented in Section “Smooth Specular Highlights”, the specular highlights in the images in this section are plainly white without any addition of other colors. Furthermore, they have a very sharp boundary.
We can implement this kind of stylized specular highlights by computing the specular reflection term of the Phong shading model and setting the fragment color to the specular reflection color times the (unattenuated) color of the light source if the specular reflection term is greater than a certain threshold, e.g. half the maximum intensity.
But what if there shouldn't been any highlights? Usually, the user would specify a black specular reflection color for this case; however, with our method this results in black highlights. One way to solve this problem is to take the opacity of the specular reflection color into account and “blend” the color of the highlight over other colors by compositing them based on the opacity of the specular color. Alpha blending as a per-fragment operation was described in Section “Transparency”. However, if all colors are known in a fragment shader, it can also be computed within a fragment shader.
In the following code snippet, fragmentColor is assumed to have already a color assigned, e.g. based on diffuse illumination. The specular color _SpecColor times the light source color _LightColor0 is then blended over fragment_Color based on the opacity of the specular color _SpecColor.a:
if (dot(normalDirection, lightDirection) > 0.0
// light source on the right side?
&& attenuation * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess) > 0.5)
// more than half highlight intensity?
{
fragmentColor = _SpecColor.a
* vec3(_LightColor0) * vec3(_SpecColor)
+ (1.0 - _SpecColor.a) * fragmentColor;
}
Is this sufficient? If you look closely at the eyes of the bull in the image to the left, you will see two pairs of specular highlights, i.e. there is more than one light source that causes specular highlights. In most tutorials, we have taken additional light sources into account by a second render pass with additive blending. However, if the color of specular highlights should not be added to other colors then additive blending should not be used. Instead, alpha blending with a (usually) opaque color for the specular highlights and transparent fragments for other fragments would be a feasible solution. (See Section “Transparency” for a description of alpha blending.)

Stylized Diffuse Illumination
[edit | edit source]The diffuse illumination in the image of the bull to the left consists of just two colors: a light brown for lit fur and a dark brown for unlit fur. The color of other parts of the bull is independent of the lighting.
One way to implement this, is to use the full diffuse reflection color whenever the diffuse reflection term of the Phong reflection model reaches a certain threshold, e.g. greater than 0, and a second color otherwise. For the fur of the bull, these two colors would be different; for the other parts, they would be the same such that there is no visual difference between lit and unlit areas. An implementation for a threshold _DiffuseThreshold to switch from the darker color _UnlitColor to the lighter color _Color (multiplied with the light source color _LightColor0) could look like this:
vec3 fragmentColor = vec3(_UnlitColor);
if (attenuation
* max(0.0, dot(normalDirection, lightDirection))
>= _DiffuseThreshold)
{
fragmentColor = vec3(_LightColor0) * vec3(_Color);
}
Is this all there is to say about the stylized diffuse illumination in the image to the left? A really close look reveals that there is a light, irregular line between the dark brown and the light brown. In fact, the situation is even more complicated and the dark brown sometimes doesn't cover all areas that would be covered by the technique described above, and sometimes it covers more than that and even goes beyond the black outline. This adds rich detail to the visual style and creates a hand-drawn appearance. On the other hand, it is very difficult to reproduce this convincingly in a shader.

Outlines
[edit | edit source]One of the characteristic features of many toon shaders are outlines in a specific color along the silhouettes of the model (usually black, but also other colors, see the cow above for an example).
There are various techniques to achieve this effect in a shader. Unity 3.3 is shipped with a toon shader in the standard assets that renders these outlines by rendering the back faces of an enlarged model in the color of the outlines (enlarged by moving the vertex positions in the direction of the surface normal vectors) and then rendering the front faces on top of them. Here we use another technique based on Section “Silhouette Enhancement”: if a fragment is determined to be close enough to a silhouette, it is set to the color of the outline. This works only for smooth surfaces, and it will generate outlines of varying thickness (which is a plus or a minus depending on the visual style). However, at least the overall thickness of the outlines should be controllable by a shader property.
Are we done yet? If you have a close look at the donkey, you will see that the outlines at its belly and in the ears are considerably thicker than other outlines. This conveys unlit areas; however, the change in thickness is continuous. One way to simulate this effect would be to let the user specify two overall outline thicknesses: one for fully lit areas and one for unlit areas (according to the diffuse reflection term of the Phong reflection model). In between these extremes, the thickness parameter could be interpolated (again according to the diffuse reflection term). This, however, makes the outlines dependent on a specific light source; therefore, the shader below renders outlines and diffuse illumination only for the first light source, which should usually be the most important one. All other light sources only render specular highlights.
The following implementation uses the mix instruction to interpolate between the _UnlitOutlineThickness (if the dot product of the diffuse reflection term is less or equal 0) and _LitOutlineThickness (if the dot product is 1). For a linear interpolation from a value a to another value b with a parameter x between 0 and 1, GLSL offers the built-in function mix(a, b, x). This interpolated value is then used as a threshold to determine whether a point is close enough to the silhouette. If it is, the fragment color is set to the color of the outline _OutlineColor:
if (dot(viewDirection, normalDirection)
< mix(_UnlitOutlineThickness, _LitOutlineThickness,
max(0.0, dot(normalDirection, lightDirection))))
{
fragmentColor =
vec3(_LightColor0) * vec3(_OutlineColor);
}
Complete Shader Code
[edit | edit source]It should be clear by now that even the few images above pose some really difficult challenges for a faithful implementation. Thus, the shader below only implements a few characteristics as described above and ignores many others. Note that the different color contributions (diffuse illumination, outlines, highlights) are given different priorities according to which should occlude which. You could also think of these priorities as different layers that are put on top of each other.
Shader "GLSL shader for toon shading" {
Properties {
_Color ("Diffuse Color", Color) = (1,1,1,1)
_UnlitColor ("Unlit Diffuse Color", Color) = (0.5,0.5,0.5,1)
_DiffuseThreshold ("Threshold for Diffuse Colors", Range(0,1))
= 0.1
_OutlineColor ("Outline Color", Color) = (0,0,0,1)
_LitOutlineThickness ("Lit Outline Thickness", Range(0,1)) = 0.1
_UnlitOutlineThickness ("Unlit Outline Thickness", Range(0,1))
= 0.4
_SpecColor ("Specular Color", Color) = (1,1,1,1)
_Shininess ("Shininess", Float) = 10
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" }
// pass for ambient light and first light source
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _UnlitColor;
uniform float _DiffuseThreshold;
uniform vec4 _OutlineColor;
uniform float _LitOutlineThickness;
uniform float _UnlitOutlineThickness;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
// default: unlit
vec3 fragmentColor = vec3(_UnlitColor);
// low priority: diffuse illumination
if (attenuation
* max(0.0, dot(normalDirection, lightDirection))
>= _DiffuseThreshold)
{
fragmentColor = vec3(_LightColor0) * vec3(_Color);
}
// higher priority: outline
if (dot(viewDirection, normalDirection)
< mix(_UnlitOutlineThickness, _LitOutlineThickness,
max(0.0, dot(normalDirection, lightDirection))))
{
fragmentColor =
vec3(_LightColor0) * vec3(_OutlineColor);
}
// highest priority: highlights
if (dot(normalDirection, lightDirection) > 0.0
// light source on the right side?
&& attenuation * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess) > 0.5)
// more than half highlight intensity?
{
fragmentColor = _SpecColor.a
* vec3(_LightColor0) * vec3(_SpecColor)
+ (1.0 - _SpecColor.a) * fragmentColor;
}
gl_FragColor = vec4(fragmentColor, 1.0);
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardAdd" }
// pass for additional light sources
Blend SrcAlpha OneMinusSrcAlpha
// blend specular highlights over framebuffer
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
uniform vec4 _UnlitColor;
uniform float _DiffuseThreshold;
uniform vec4 _OutlineColor;
uniform float _LitOutlineThickness;
uniform float _UnlitOutlineThickness;
uniform vec4 _SpecColor;
uniform float _Shininess;
// The following built-in uniforms (except _LightColor0)
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec3 _WorldSpaceCameraPos;
// camera position in world space
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 _WorldSpaceLightPos0;
// direction to or position of light source
uniform vec4 _LightColor0;
// color of light source (from "Lighting.cginc")
varying vec4 position;
// position of the vertex (and fragment) in world space
varying vec3 varyingNormalDirection;
// surface normal vector in world space
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object; // unity_Scale.w
// is unnecessary because we normalize vectors
position = modelMatrix * gl_Vertex;
varyingNormalDirection = normalize(vec3(
vec4(gl_Normal, 0.0) * modelMatrixInverse));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection =
normalize(_WorldSpaceCameraPos - vec3(position));
vec3 lightDirection;
float attenuation;
if (0.0 == _WorldSpaceLightPos0.w) // directional light?
{
attenuation = 1.0; // no attenuation
lightDirection = normalize(vec3(_WorldSpaceLightPos0));
}
else // point or spot light
{
vec3 vertexToLightSource =
vec3(_WorldSpaceLightPos0 - position);
float distance = length(vertexToLightSource);
attenuation = 1.0 / distance; // linear attenuation
lightDirection = normalize(vertexToLightSource);
}
vec4 fragmentColor = vec4(0.0, 0.0, 0.0, 0.0);
if (dot(normalDirection, lightDirection) > 0.0
// light source on the right side?
&& attenuation * pow(max(0.0, dot(
reflect(-lightDirection, normalDirection),
viewDirection)), _Shininess) > 0.5)
// more than half highlight intensity?
{
fragmentColor =
vec4(_LightColor0.rgb, 1.0) * _SpecColor;
}
gl_FragColor = fragmentColor;
}
#endif
ENDGLSL
}
}
// The definition of a fallback shader should be commented out
// during development:
// Fallback "Specular"
}
One problem with this shader are the hard edges between colors, which often result in noticeable aliasing, in particular at the outlines. This could be alleviated by using the smoothstep function to provide a smoother transition.
Summary
[edit | edit source]Congratulations, you have reached the end of this tutorial. We have seen:
- What toon shading, cel shading, and non-photorealistic rendering are.
- How some of the non-photorealistic rendering techniques are used in toon shading.
- How to implement these techniques in a shader.
Further Reading
[edit | edit source]If you still want to know more
- about the Phong reflection model and the per-pixel lighting, you should read Section “Smooth Specular Highlights”.
- about the computation of silhouettes, you should read Section “Silhouette Enhancement”.
- about blending, you should read Section “Transparency”.
- about non-photorealistic rendering techniques, you could read Chapter 18 of the book “OpenGL Shading Language” (3rd edition) by Randi Rost et al., published 2009 by Addison-Wesley.
Screen Overlays
[edit | edit source]
This tutorial covers screen overlays, which are also known as “GUI Textures” in Unity.
It is the first tutorial of a series of tutorials on non-standard vertex transformations, which deviate from the standard vertex transformations that are described in Section “Vertex Transformations”. This particular tutorial uses texturing as described in Section “Textured Spheres” and blending as described in Section “Transparency”.
Unity's GUI Textures
[edit | edit source]There are many applications for screen overlays (i.e. GUI textures in Unity's terminology), e.g. titles as in the image to the left, but also other GUI (graphical user interface) elements such as buttons or status information. The common feature of these elements is that they should always appear on top of the scene and never be occluded by any other objects. Neither should these elements be affected by any of the camera movements. Thus, the vertex transformation should go directly from object space to screen space. Unity's GUI textures allow us to render this kind of element by rendering a texture image at a specified position on the screen. This tutorial tries to reproduce the functionality of GUI textures with the help of shaders. Usually, you would still use GUI textures instead of such a shader; however, the shader allows for a lot more flexibility since you can adapt it in any way you want while GUI textures only offer a limited set of possibilities. (For example, you could change the shader such that the GPU spends less time on rasterizing the triangles that are occluded by an opaque GUI texture.)
Simulating GUI Textures with a GLSL Shader
[edit | edit source]The position of Unity's GUI textures is specified by an X and a Y coordinate of the lower, left corner of the rendered rectangle in pixels with at the center of the screen and a Width and Height of the rendered rectangle in pixels. To simulate GUI textures, we use similar shader properties:
Properties {
_MainTex ("Texture", Rect) = "white" {}
_Color ("Color", Color) = (1.0, 1.0, 1.0, 1.0)
_X ("X", Float) = 0.0
_Y ("Y", Float) = 0.0
_Width ("Width", Float) = 128
_Height ("Height", Float) = 128
}
and the corresponding uniforms
uniform sampler2D _MainTex;
uniform vec4 _Color;
uniform float _X;
uniform float _Y;
uniform float _Width;
uniform float _Height;
For the actual object, we could use a mesh that consists of just two triangles to form a rectangle. However, we can also just use the default cube object since back-face culling (and culling of triangles that are degenerated to edges) allows us to make sure that only two triangles of the cube are rasterized. The corners of the default cube object have coordinates and in object space, i.e., the lower, left corner of the rectangle is at and the upper, right corner is at . To transform these coordinates to the user-specified coordinates in screen space, we first transform them to raster positions in pixels where is at the lower, left corner of the screen:
uniform vec4 _ScreenParams; // x = width; y = height;
// z = 1 + 1.0/width; w = 1 + 1.0/height
...
#ifdef VERTEX
void main()
{
vec2 rasterPosition = vec2(
_X + _ScreenParams.x / 2.0
+ _Width * (gl_Vertex.x + 0.5),
_Y + _ScreenParams.y / 2.0
+ _Height * (gl_Vertex.y + 0.5));
...
This transformation transforms the lower, left corner of the front face of our cube from in object space to the raster position vec2(_X + _ScreenParams.x / 2.0, _Y + _ScreenParams.y / 2.0), where _ScreenParams.x is the screen width in pixels and _ScreenParams.y is the height in pixels. The upper, right corner is transformed from to vec2(_X + _ScreenParams.x / 2.0 + _Width, _Y + _ScreenParams.y / 2.0 + _Height). Raster positions are convenient and, in fact, they are often used in OpenGL; however, they are not quite what we need here.
The output of the vertex shader in gl_Position is in the so-called “clip space” as discussed in Section “Vertex Transformations”. The GPU transforms these coordinates to normalized device coordinates between and by dividing them by the fourth coordinate gl_Position.w in the perspective division. If we set this fourth coordinate to , this division doesn't change anything; thus, we can think of the first three coordinates of gl_Position as coordinates in normalized device coordinates, where specifies the lower, left corner of the screen on the near plane and specifies the upper, right corner on the near plane. (We should use the near plane to make sure that the rectangle is in front of everything else.) In order to specify any screen position in gl_Position, we have to specify it in this coordinate system. Fortunately, transforming a raster position to normalized device coordinates is not too difficult:
gl_Position = vec4(
2.0 * rasterPosition.x / _ScreenParams.x - 1.0,
2.0 * rasterPosition.y / _ScreenParams.y - 1.0,
-1.0, // near plane
1.0 // all coordinates are divided by this coordinate
);
As you can easily check, this transforms the raster position vec2(0,0) to normalized device coordinates and the raster position vec2(_ScreenParams.x, _ScreenParams.y) to , which is exactly what we need.
This is all we need for the vertex transformation from object space to screen space. However, we still need to compute appropriate texture coordinates in order to look up the texture image at the correct position. Texture coordinates should be between and , which is actually easy to compute from the vertex coordinates in object space between and :
textureCoords =
vec4(gl_Vertex.x + 0.5, gl_Vertex.y + 0.5, 0.0, 0.0);
// for a cube, gl_Vertex.x and gl_Vertex.y
// are -0.5 or 0.5
With the varying variable textureCoords, we can then use a simple fragment program to look up the color in the texture image and modulate it with the user-specified color _Color:
#ifdef FRAGMENT
void main()
{
gl_FragColor =
_Color * texture2D (_MainTex, vec2(textureCoords));
}
#endif
That's it.
Complete Shader Code
[edit | edit source]If we put all the pieces together, we get the following shader, which uses the Overlay queue to render the object after everything else, and uses alpha blending (see Section “Transparency”) to allow for transparent textures. It also deactivates the depth test to make sure that the texture is never occluded:
Shader "GLSL shader for screen overlays" {
Properties {
_MainTex ("Texture", Rect) = "white" {}
_Color ("Color", Color) = (1.0, 1.0, 1.0, 1.0)
_X ("X", Float) = 0.0
_Y ("Y", Float) = 0.0
_Width ("Width", Float) = 128
_Height ("Height", Float) = 128
}
SubShader {
Tags { "Queue" = "Overlay" } // render after everything else
Pass {
Blend SrcAlpha OneMinusSrcAlpha // use alpha blending
ZTest Always // deactivate depth test
GLSLPROGRAM
// User-specified uniforms
uniform sampler2D _MainTex;
uniform vec4 _Color;
uniform float _X;
uniform float _Y;
uniform float _Width;
uniform float _Height;
// The following built-in uniforms
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform vec4 _ScreenParams; // x = width; y = height;
// z = 1 + 1.0/width; w = 1 + 1.0/height
// Varyings
varying vec4 textureCoords;
#ifdef VERTEX
void main()
{
vec2 rasterPosition = vec2(
_X + _ScreenParams.x / 2.0
+ _Width * (gl_Vertex.x + 0.5),
_Y + _ScreenParams.y / 2.0
+ _Height * (gl_Vertex.y + 0.5));
gl_Position = vec4(
2.0 * rasterPosition.x / _ScreenParams.x - 1.0,
2.0 * rasterPosition.y / _ScreenParams.y - 1.0,
-1.0, // near plane is -1.0
1.0);
textureCoords =
vec4(gl_Vertex.x + 0.5, gl_Vertex.y + 0.5, 0.0, 0.0);
// for a cube, gl_Vertex.x and gl_Vertex.y
// are -0.5 or 0.5
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor =
_Color * texture2D (_MainTex, vec2(textureCoords));
}
#endif
ENDGLSL
}
}
}
When you use this shader for a cube object, the texture image can appear and disappear depending on the orientation of the camera. This is due to clipping by Unity, which doesn't render objects that are completely outside of the region of the scene that is visible in the camera (the view frustum). This clipping is based on the conventional transformation of game objects, which doesn't make sense for our shader. In order to deactivate this clipping, we can simply make the cube object a child of the camera (by dragging it over the camera in the Hierarchy View). If the cube object is then placed in front of the camera, it will always stay in the same relative position, and thus it won't be clipped by Unity. (At least not in the game view.)
Changes for Opaque Screen Overlays
[edit | edit source]Many changes to the shader are conceivable, e.g. a different blend mode or a different depth to have a few objects of the 3D scene in front of the overlay. Here we will only look at opaque overlays.
An opaque screen overlay will occlude triangles of the scene. If the GPU was aware of this occlusion, it wouldn't have to rasterize these occluded triangles (e.g. by using deferred rendering or early depth tests). In order to make sure that the GPU has any chance to apply these optimizations, we have to render the screen overlay first, by setting
Tags { "Queue" = "Background" }
Also, we should avoid blending by removing the Blend instruction. With these changes, opaque screen overlays are likely to improve performance instead of costing rasterization performance.
Summary
[edit | edit source]Congratulation, you have reached the end of another tutorial. We have seen:
- How to simulate GUI textures with a GLSL shader.
- How to modify the shader for opaque screen overlays.
Further Reading
[edit | edit source]If you still want to know more
- about texturing, you should read Section “Textured Spheres”.
- about blending, you should read Section “Transparency”.
- about object space, screen space, clip space, normalized device coordinates, perspective division, etc., you should read the description of the standard vertex transformations in Section “Vertex Transformations”.
Billboards
[edit | edit source]
This tutorial introduces billboards.
It is based on Section “Textured Spheres” and the discussion in Section “Vertex Transformations”.
Billboards
[edit | edit source]In computer graphics, billboards are textured rectangles that are transformed such that they always appear parallel to the view plane. Thus, they are similar to billboards along highways in that they are rotated for best visibility. However, they are different from highway billboards since they are dynamically rotated to always offer best visibility.
The main use of billboards is to replace complex three-dimensional models (e.g. grass, bushes, or even trees) by two-dimensional images. In fact, Unity also uses billboards to render grass. Moreover, billboards are often used to render two-dimensional sprites. In both applications, it is crucial that the billboard is always aligned parallel to the view plane in order to keep up the illusion of a three-dimensional shape although only a two-dimensional image is rendered.
Vertex Transformation for Billboards
[edit | edit source]Similarly to Section “Skyboxes”, we are going to use the default cube object to render a billboard. The basic idea is to transform only the origin of the object space to view space with the standard transformation gl_ModelViewMatrix. (In homogeneous coordinates all points have a 1 as fourth coordinate; see the discussion in Section “Vertex Transformations”.) View space is just a rotated version of world space with the plane parallel to the view plane as discussed in Section “Vertex Transformations”. Thus, this is the correct space to construct an appropriately rotated billboard. We add the and object coordinates (gl_Vertex.x and gl_Vertex.y) to the transformed origin in view coordinates and then transform the result with the projection matrix gl_ProjectionMatrix:
gl_Position = gl_ProjectionMatrix * (gl_ModelViewMatrix * vec4(0.0, 0.0, 0.0, 1.0) + vec4(gl_Vertex.x, gl_Vertex.y, 0.0, 0.0));
Apart from this, we only have to compute texture coordinates, which is done the same way as in Section “Screen Overlays”:
textureCoords = vec4(gl_Vertex.x + 0.5, gl_Vertex.y + 0.5, 0.0, 0.0);
Then the fragment shader just looks up the color at the interpolated texture coordinates.
Complete Shader Code
[edit | edit source]The complete shader code for the standard cube object is now:
Shader "GLSL shader for billboards" {
Properties {
_MainTex ("Texture Image", 2D) = "white" {}
}
SubShader {
Pass {
GLSLPROGRAM
// User-specified uniforms
uniform sampler2D _MainTex;
// Varyings
varying vec4 textureCoords;
#ifdef VERTEX
void main()
{
gl_Position = gl_ProjectionMatrix
* (gl_ModelViewMatrix * vec4(0.0, 0.0, 0.0, 1.0)
+ vec4(gl_Vertex.x, gl_Vertex.y, 0.0, 0.0));
textureCoords =
vec4(gl_Vertex.x + 0.5, gl_Vertex.y + 0.5, 0.0, 0.0);
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = texture2D(_MainTex, vec2(textureCoords));
}
#endif
ENDGLSL
}
}
}
Note that we never apply the model matrix to the object coordinates because we don't want to rotate them. However, this means that we also cannot scale them. Nonetheless, if you specify scale factors for the cube in Unity, you will notice that the billboard is actually scaled. The reason is that Unity performs the scaling on the object coordinates before they are sent to the vertex shader (unless all three scale factors are positive and equal, then the scaling is specified by 1.0 / unity_Scale.w). Thus, in order to scale the billboard you can either use the scaling by Unity (with different scale factors for and ) or you can introduce additional shader properties for scaling the object coordinates in the vertex shader.
Summary
[edit | edit source]Congratulations, you made it to the end of this tutorial. We have seen:
- How to transform and texture a cube in order to render a view-aligned billboard.
Further Reading
[edit | edit source]If you still want to learn more
- about object space, world space, view space,
gl_ModelViewMatrixandgl_ProjectionMatrix, you should read the description in Section “Vertex Transformations”. - about texturing, you should read Section “Textured Spheres”.
Nonlinear Deformations
[edit | edit source]
This tutorial introduces vertex blending as an example of a nonlinear deformation. The main application is actually the rendering of skinned meshes.
While this tutorial is not based on any other specific tutorial, a good understanding of Section “Vertex Transformations” is very useful.
Blending between Two Model Transformations
[edit | edit source]Most deformations of meshes cannot be modeled by the affine transformations with 4×4 matrices that are discussed in Section “Vertex Transformations”. The deformation of bodies by tight corsets is just one example. A more important example in computer graphics is the deformation of meshes when joints are bent, e.g. elbows or knees.
This tutorial introduces vertex blending to implement some of these deformations. The basic idea is to apply multiple model transformations in the vertex shader (in this tutorial we use only two model transformations) and then blend the transformed vertices, i.e. compute a weighted average of them with weights that have to be specified for each vertex. For example, the deformation of the skin near a joint of a skeleton is mainly influenced by the position and orientation of the two (rigid) bones meeting in the joint. Thus, the positions and orientations of the two bones define two affine transformations. Different points on the skin are influenced differently by the two bones: points at the joint might be influenced equally by the two bones while points farther from the joint around one bone are more strongly influenced by that bone than the other. These different strengths of the influence of the two bones can be implemented by using different weights in the weighted average of the two transformations.
For the purpose of this tutorial, we use two uniform transformations mat4 _Trafo0 and mat4 _Trafo1, which are specified by the user. To this end a small JavaScript (which should be attached to the mesh that should be deformed) allows us to specify two other game objects and copies their model transformations to the uniforms of the shader:
@script ExecuteInEditMode()
public var bone0 : GameObject;
public var bone1 : GameObject;
function Update ()
{
if (null != bone0)
{
renderer.sharedMaterial.SetMatrix("_Trafo0",
bone0.renderer.localToWorldMatrix);
}
if (null != bone1)
{
renderer.sharedMaterial.SetMatrix("_Trafo1",
bone1.renderer.localToWorldMatrix);
}
if (null != bone0 && null != bone1)
{
transform.position = 0.5 * (bone0.transform.position
+ bone1.transform.position);
transform.rotation = bone0.transform.rotation;
}
}
The two other game objects could be anything — I like cubes with one of the built-in semitransparent shaders such that their position and orientation is visible but they don't occlude the deformed mesh.
In this tutorial, the weight for the blending with the transformation _Trafo0 is set to gl_Vertex.z + 0.5:
float weight0 = gl_Vertex.z + 0.5;
and the other weight is 1.0 - weight0. Thus, the part with positive gl_Vertex.z coordinates is influenced more by _Trafo0 and the other part is influenced more by _Trafo1. In general, the weights are application dependent and the user should be allowed to specify weights for each vertex.
The application of the two transformations and the weighted average can be written this way:
vec4 blendedVertex = weight0 * (_Trafo0 * gl_Vertex) + (1.0 - weight0) * (_Trafo1 * gl_Vertex);
Then the blended vertex has to be multiplied with the view matrix and the projection matrix. The view transformation is not available directly but it can be computed by multiplying the model-view matrix (which is the product of the view matrix and the model matrix) with the inverse model matrix (which is available as _World2Object times unity_Scale.w except for the bottom-right element, which is 1):
mat4 modelMatrixInverse = _World2Object * unity_Scale.w;
modelMatrixInverse[3][3] = 1.0;
mat4 viewMatrix = gl_ModelViewMatrix * modelMatrixInverse;
gl_Position = gl_ProjectionMatrix * viewMatrix * blendedVertex;
In order to illustrate the different weights, we visualize weight0 by the red component and 1.0 - weight0 by the green component of a color (which is set in the fragment shader):
color = vec4(weight0, 1.0 - weight0, 0.0, 1.0);
For an actual application, we could also transform the normal vector by the two corresponding transposed inverse model transformations and perform per-pixel lighting in the fragment shader.
Complete Shader Code
[edit | edit source]All in all, the shader code looks like this:
Shader "GLSL shader for vertex blending" {
SubShader {
Pass {
GLSLPROGRAM
// Uniforms set by a script
uniform mat4 _Trafo0; // model transformation of bone0
uniform mat4 _Trafo1; // model transformation of bone1
// The following built-in uniforms
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
uniform vec4 unity_Scale; // w = 1/scale
uniform mat4 _World2Object; // inverse model matrix
// all but the bottom-right element should be
// multiplied with unity_Scale.w
// Varyings
varying vec4 color;
#ifdef VERTEX
void main()
{
float weight0 = gl_Vertex.z + 0.5; // depends on the mesh
vec4 blendedVertex = weight0 * (_Trafo0 * gl_Vertex)
+ (1.0 - weight0) * (_Trafo1 * gl_Vertex);
mat4 modelMatrixInverse = _World2Object * unity_Scale.w;
modelMatrixInverse[3][3] = 1.0;
mat4 viewMatrix = gl_ModelViewMatrix * modelMatrixInverse;
gl_Position =
gl_ProjectionMatrix * viewMatrix * blendedVertex;
color = vec4(weight0, 1.0 - weight0, 0.0, 1.0);
// visualize weight0 as red and weight1 as green
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = color;
}
#endif
ENDGLSL
}
}
}
This is, of course, only an illustration of the concept but it can already be used for some interesting nonlinear deformations such as twists around the axis.
For skinned meshes in skeletal animation, many more bones (i.e. model transformations) are necessary and each vertex has to specify which bone (using, for example, an index) contributes with which weight to the weighted average. However, Unity computes the blending of vertices in software; thus, this topic is less relevant for Unity programmers.
Summary
[edit | edit source]Congratulations, you have reached the end of another tutorial. We have seen:
- How to blend vertices that are transformed by two model matrices.
- How this technique can be used for nonlinear transformations and skinned meshes.
Further Reading
[edit | edit source]If you still want to learn more
- about the model transformation, the view transformation, and the projection, you should read the description in Section “Vertex Transformations”.
- about vertex skinning, you could read the section about vertex skinning in Chapter 8 of the “OpenGL ES 2.0 Programming Guide” by Aaftab Munshi, Dan Ginsburg, and Dave Shreiner, published 2009 by Addison-Wesley.
Shadows on Planes
[edit | edit source]
This tutorial covers the projection of shadows onto planes.
It is not based on any particular tutorial; however, some understanding of Section “Vertex Transformations” is useful.
Projecting Hard Shadows onto Planes
[edit | edit source]Computing realistic shadows in real time is difficult. However, there are certain cases that are a lot easier. Projecting a hard shadow (i.e. a shadow without penumbra; see Section “Soft Shadows of Spheres”) onto a plane is one of these cases. The idea is to render the shadow by rendering the shadow-casting object in the color of the shadow with the vertices projected just above the shadow-receiving plane.

Projecting an Object onto a Plane
[edit | edit source]In order to render the projected shadow, we have to project the object onto a plane. In order to specify the plane, we will use the local coordinate system of the default plane game object. Thus, we can easily modify the position and orientation of the plane by editing the plane object. In the coordinate system of that game object, the actual plane is just the plane, which is spanned by the and axes.
Projecting an object in a vertex shader means to project each vertex. This could be done with a projection matrix similar to the one discussed in Section “Vertex Transformations”. However, those matrices are somewhat difficult to compute and debug. Therefore, we will take another approach and compute the projection with a bit of vector arithmetics. The illustration to the left shows the projection of a point P in the direction of light L onto a shadow-receiving plane. (Note that the vector L is in the opposite direction than the light vectors that are usually employed in lighting computations.) In order to move the point P to the plane, we add a scaled version of L. The scaling factor turns out to be the distance of P to the plane divided by the length of L in the direction of the normal vector of the plane (because of similar triangles as indicated by the gray lines). In the coordinate system of the plane, where the normal vector is just the axis, we can also use the ratio of the coordinate of the point P divided by the negated coordinate of the vector L.
Thus, the vertex shader could look like this:
GLSLPROGRAM
// User-specified uniforms
uniform mat4 _World2Receiver; // transformation from
// world coordinates to the coordinate system of the plane
// The following built-in uniforms
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 unity_Scale; // w = 1/uniform scale;
// should be multiplied to _World2Object
uniform vec4 _WorldSpaceLightPos0;
// position or direction of light source
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object * unity_Scale.w;
modelMatrixInverse[3][3] = 1.0;
mat4 viewMatrix = gl_ModelViewMatrix * modelMatrixInverse;
vec4 lightDirection;
if (0.0 != _WorldSpaceLightPos0.w) // point or spot light?
{
lightDirection = normalize(
modelMatrix * gl_Vertex - _WorldSpaceLightPos0);
}
else // directional light
{
lightDirection = -normalize(_WorldSpaceLightPos0);
}
vec4 vertexInWorldSpace = modelMatrix * gl_Vertex;
float distanceOfVertex =
(_World2Receiver * vertexInWorldSpace).y;
// = height over plane
float lengthOfLightDirectionInY =
(_World2Receiver * lightDirection).y;
// = length in y direction
lightDirection = lightDirection
* (distanceOfVertex / (-lengthOfLightDirectionInY));
gl_Position = gl_ProjectionMatrix * (viewMatrix
* (vertexInWorldSpace + lightDirection));
}
#endif
...
The uniform _World2Receiver is best set with the help of a small script that should be attached to the shadow-casting object:
@script ExecuteInEditMode()
public var plane : GameObject;
function Update ()
{
if (null != plane)
{
renderer.sharedMaterial.SetMatrix("_World2Receiver",
plane.renderer.worldToLocalMatrix);
}
}
The script requires the user to specify the shadow-receiving plane object and sets the uniform _World2Receiver accordingly.
Complete Shader Code
[edit | edit source]For the complete shader code we improve the performance by noting that the coordinate of a matrix-vector product is just the dot product of the second row (i.e. the first when starting with 0) of the matrix and the vector. Furthermore, we improve the robustness by not moving the vertex when it is below the plane, neither when the light is directed upwards. Additionally, we try to make sure that the shadow is on top of the plane with this instruction:
Offset -1.0, -2.0
This reduces the depth of the rasterized triangles a bit such that they always occlude other triangles of approximately the same depth.
The first pass of the shader renders the shadow-casting object while the second pass renders the projected shadow. In an actual application, the first pass could be replaced by one or more passes to compute the lighting of the shadow-casting object.
Shader "GLSL planar shadow" {
Properties {
_Color ("Object's Color", Color) = (0,1,0,1)
_ShadowColor ("Shadow's Color", Color) = (0,0,0,1)
}
SubShader {
Pass {
Tags { "LightMode" = "ForwardBase" } // rendering of object
GLSLPROGRAM
// User-specified properties
uniform vec4 _Color;
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = _Color;
}
#endif
ENDGLSL
}
Pass {
Tags { "LightMode" = "ForwardBase" }
// rendering of projected shadow
Offset -1.0, -2.0
// make sure shadow polygons are on top of shadow receiver
GLSLPROGRAM
// User-specified uniforms
uniform vec4 _ShadowColor;
uniform mat4 _World2Receiver; // set by script
// The following built-in uniforms )
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
uniform mat4 _World2Object; // inverse model matrix
uniform vec4 unity_Scale; // w = 1/uniform scale;
// should be multiplied to _World2Object
uniform vec4 _WorldSpaceLightPos0;
// position or direction of light source
#ifdef VERTEX
void main()
{
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object * unity_Scale.w;
modelMatrixInverse[3][3] = 1.0;
mat4 viewMatrix = gl_ModelViewMatrix * modelMatrixInverse;
vec4 lightDirection;
if (0.0 != _WorldSpaceLightPos0.w)
{
// point or spot light
lightDirection = normalize(
modelMatrix * gl_Vertex - _WorldSpaceLightPos0);
}
else
{
// directional light
lightDirection = -normalize(_WorldSpaceLightPos0);
}
vec4 vertexInWorldSpace = modelMatrix * gl_Vertex;
vec4 world2ReceiverRow1 =
vec4(_World2Receiver[0][1], _World2Receiver[1][1],
_World2Receiver[2][1], _World2Receiver[3][1]);
float distanceOfVertex =
dot(world2ReceiverRow1, vertexInWorldSpace);
// = (_World2Receiver * vertexInWorldSpace).y
// = height over plane
float lengthOfLightDirectionInY =
dot(world2ReceiverRow1, lightDirection);
// = (_World2Receiver * lightDirection).y
// = length in y direction
if (distanceOfVertex > 0.0 && lengthOfLightDirectionInY < 0.0)
{
lightDirection = lightDirection
* (distanceOfVertex / (-lengthOfLightDirectionInY));
}
else
{
lightDirection = vec4(0.0, 0.0, 0.0, 0.0);
// don't move vertex
}
gl_Position = gl_ProjectionMatrix * (viewMatrix
* (vertexInWorldSpace + lightDirection));
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = _ShadowColor;
}
#endif
ENDGLSL
}
}
}
Further Improvements of the Fragment Shader
[edit | edit source]There are a couple of things that could be improved, in particular in the fragment shader:
- Fragments of the shadow that are outside of the rectangular plane object could be removed with the
discardinstruction, which was discussed in Section “Cutaways”. - If the plane is textured, this texturing could be integrated by using only local vertex coordinates for the texture lookup (also in the shader of the plane object) and specifying the texture of the plane as a shader property of the shadow-casting object.
- Soft shadows could be faked by computing the lighting of the plane in this shader and attenuating it depending on the angle of the surface normal vector of the shadow-casting object to the light direction similar to the approach in Section “Silhouette Enhancement”.
Summary
[edit | edit source]Congratulations, this is the end of this tutorial. We have seen:
- How to project a vertex in the direction of light onto a plane.
- How to implement this technique to project a shadow onto a plane.
Further Reading
[edit | edit source]If you still want to learn more
- about the model transformation, the view transformation, and the projection, you should read the description in Section “Vertex Transformations”.
- about setting up a projection matrix to project the shadow, you could read Section 9.4.1 of the SIGGRAPH '98 Course “Advanced Graphics Programming Techniques Using OpenGL” organized by Tom McReynolds, which is available online.
Mirrors
[edit | edit source]This tutorial covers the rendering of virtual images of objects in plane mirrors.
It is based on blending as described in Section “Transparency” and requires some understanding of Section “Vertex Transformations”.
Virtual Images in Plane Mirrors
[edit | edit source]The image we see in a plane mirror is called a “virtual image” because it is the same as the image of the real scene except that all positions are mirrored at the plane of the mirror; thus, we don't see the real scene but a “virtual” image of it.
This transformation of a real object to a virtual object can be computed by transforming each position from world space into the local coordinate system of the mirror; negating the coordinate (assuming that the mirror plane is spanned by the and axes); and transforming the resulting position back to world space. This suggests a very straightforward approach to rendering virtual images of game objects by using another shader pass with a vertex shader that mirrors every vertex and normal vector, and a fragment shader that mirrors the position of light sources before computing the shading. (In fact, the light source at the original positions might also be taken into account because they represent light that is reflected by the mirror before reaching the real object.) There isn't anything wrong with this approach except that it is very limited: no other objects may be behind the mirror plane (not even partially) and the space behind the mirror plane must only be visible through the mirror. This is fine for mirrors on walls of a box that contains the whole scene if all the geometry outside the box can be removed. However, it doesn't work for mirrors with objects behind it (as in the painting by Velázquez) nor for semitransparent mirrors, for example glass windows.
Placing the Virtual Objects
[edit | edit source]It turns out that implementing a more general solution is not straightforward in the free version of Unity because neither rendering to textures (which would allow us to render the scene from a virtual camera position behind the mirror) nor stencil buffers (which would allow us to restrict the rendering to the region of the mirror) are available in the free version of Unity.
I came up with the following solution: First, every game object that might appear in the mirror has to have a virtual “Doppelgänger”, i.e. a copy that follows all the movements of the real game object but with positions mirrored at the mirror plane. Each of these virtual objects needs a script that sets its position and orientation according to the corresponding real object and the mirror plane, which are specified by public variables:
@script ExecuteInEditMode()
var objectBeforeMirror : GameObject;
var mirrorPlane : GameObject;
function Update ()
{
if (null != mirrorPlane)
{
renderer.sharedMaterial.SetMatrix("_WorldToMirror",
mirrorPlane.renderer.worldToLocalMatrix);
if (null != objectBeforeMirror)
{
transform.position = objectBeforeMirror.transform.position;
transform.rotation = objectBeforeMirror.transform.rotation;
transform.localScale =
-objectBeforeMirror.transform.localScale;
transform.RotateAround(objectBeforeMirror.transform.position,
mirrorPlane.transform.TransformDirection(
Vector3(0.0, 1.0, 0.0)), 180.0);
var positionInMirrorSpace : Vector3 =
mirrorPlane.transform.InverseTransformPoint(
objectBeforeMirror.transform.position);
positionInMirrorSpace.y = -positionInMirrorSpace.y;
transform.position = mirrorPlane.transform.TransformPoint(
positionInMirrorSpace);
}
}
}
The origin of the local coordinate system (objectBeforeMirror.transform.position) is transformed as described above; i.e., it's transformed to the local coordinate system of the mirror with mirrorPlane.transform.InverseTransformPoint(), then the coordinate is reflected, and then it is transformed back to world space with mirrorPlane.transform.TransformPoint(). However, the orientation is a bit difficult to specify in JavaScript: we have to reflect all coordinates (transform.localScale = -objectBeforeMirror.transform.localScale) and rotate the virtual object by 180° around the surface normal vector of the mirror (Vector3(0.0, 1.0, 0.0) transformed to world coordinates. This does the trick because a rotation around 180° corresponds to the reflection of two axes orthogonal to the rotation axis. Thus, this rotation undoes the previous reflection for two axes and we are left with the one reflection in the direction of the rotation axis, which was chosen to be the normal of the mirror.
Of course, the virtual objects should always follow the real object, i.e. they shouldn't collide with other objects nor be influenced by physics in any other way. Using this script on all virtual objects is already sufficient for the case mentioned above: no real objects behind the mirror plane and no other way to see the space behind the mirror plane except through the mirror. In other cases we have to render the mirror in order to occlude the real objects behind it.
Rendering the Mirror
[edit | edit source]Now things become a bit tricky. Let's list what we want to achieve:
- Real objects behind the mirror should be occluded by the mirror.
- The mirror should be occluded by the virtual objects (which are actually behind it).
- Real objects in front of the mirror should occlude the mirror and any virtual objects.
- Virtual objects should only be visible in the mirror, not outside of it.
If we could restrict rendering to an arbitrary part of the screen (e.g. with a stencil buffer), this would be easy: render all geometry including an opaque mirror; then restrict the rendering to the visible parts of the mirror (i.e. not the parts that are occluded by other real objects); clear the depth buffer in these visible parts of the mirror; and render all virtual objects. It's straightforward if we had a stencil buffer.
Since we don't have a stencil buffer, we use the alpha component (a.k.a. opacity or A component) of the framebuffer as a substitute (similar to the technique used in Section “Translucent Bodies”). In the first pass of the shader for the mirror, all pixels in the visible part of the mirror (i.e. the part that is not occluded by real objects in front of it) will be marked by an alpha component of 0, while pixels in the rest of the screen should have an alpha component of 1. The first problem is that we have to make sure that the rest of the screen has an alpha component of 1, i.e. all background shaders and object shaders should set alpha to 1. For example, Unity's skyboxes don't set alpha to 1; thus, we have to modify and replace all those shaders that don't set alpha to 1. Let's assume that we can do that. Then the first pass of the shader for the mirror is:
// 1st pass: mark mirror with alpha = 0
Pass {
GLSLPROGRAM
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(1.0, 0.0, 0.0, 0.0);
// this color should never be visible,
// only alpha is important
}
#endif
ENDGLSL
}
How does this help us to limit the rendering to the pixels with alpha equal to 0? It doesn't. However, it does help us to restrict any changes of colors in the framebuffer by using a clever blend equation (see Section “Transparency”):
Blend OneMinusDstAlpha DstAlpha
We can think of the blend equation as:
vec4 result = vec4(1.0 - pixel_color.a) * gl_FragColor + vec4(pixel_color.a) * pixel_color;
where pixel_color is the color of a pixel in the framebuffer. Let's see what the expression is for pixel_color.a equal to 1 (i.e. outside of the visible part of the mirror):
vec4(1.0 - 1.0) * gl_FragColor + vec4(1.0) * pixel_color == pixel_color
Thus, if pixel_color.a is equal to 1, the blending equation makes sure that we don't change the pixel color in the framebuffer. What happens if pixel_color.a is equal to 0 (i.e. inside the visible part of the mirror)?
vec4(1.0 - 0.0) * gl_FragColor + vec4(0.0) * pixel_color == gl_FragColor
In this case, the pixel color of the framebuffer will be set to the fragment color that was set in the fragment shader. Thus, using this blend equation, our fragment shader will only change the color of pixels with an alpha component of 0. Note that the alpha component in gl_FragColor should also be 0 such that the pixels are still marked as part of the visible region of the mirror.
That was the first pass. The second pass has to clear the depth buffer before we start to render the virtual objects such that we can use the normal depth test to compute occlusions (see Section “Per-Fragment Operations”). Actually, it doesn't matter whether we clear the depth buffer only for the pixels in the visible part of the mirror or for all pixels of the screen because we won't change the colors of any pixels with alpha equal to 1 anyways. In fact, this is very fortunate because (without stencil test) we cannot limit the clearing of the depth buffer to the visible part of the mirror. Instead, we clear the depth buffer for the whole mirror by transforming the vertices to the far clipping plane, i.e. the maximum depth.
As explained in Section “Vertex Transformations”, the output of the vertex shader in gl_Position is divided automatically by the fourth coordinate gl_Position.w to compute normalized device coordinates between -1 and +1. In fact, a coordinate of +1 represents the maximum depth; thus, this is what we are aiming for. However, because of that automatic (perspective) division by gl_Position.w, we have to set gl_Position.z to gl_Position.w in order to get a normalized device coordinate of +1. Here is the second pass of the mirror shader:
// 2nd pass: set depth to far plane such that
// we can use the normal depth test for the reflected geometry
Pass {
ZTest Always
Blend OneMinusDstAlpha DstAlpha
GLSLPROGRAM
uniform vec4 _Color;
// user-specified background color in the mirror
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
gl_Position.z = gl_Position.w;
// the perspective division will divide gl_Position.z
// by gl_Position.w; thus, the depth is 1.0,
// which represents the far clipping plane
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(_Color.rgb, 0.0);
// set alpha to 0.0 and
// the color to the user-specified background color
}
#endif
ENDGLSL
}
The ZTest is set to Always in order to deactivate it. This is necessary because our vertices are actually behind the mirror (in order to reset the depth buffer); thus, the fragments would fail a normal depth test. We use the blend equation which was discussed above to set the user-specified background color of the mirror. (If there is a skybox in your scene, you would have to compute the mirrored view direction and look up the environment map here; see Section “Skyboxes”.)
This is the shader for the mirror. Here is the complete shader code, which uses "Transparent+10" to make sure that it is rendered after all real objects (including transparent objects) have been rendered:
Shader "GLSL shader for mirrors" {
Properties {
_Color ("Mirrors's Color", Color) = (1, 1, 1, 1)
}
SubShader {
Tags { "Queue" = "Transparent+10" }
// draw after all other geometry has been drawn
// because we mess with the depth buffer
// 1st pass: mark mirror with alpha = 0
Pass {
GLSLPROGRAM
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(1.0, 0.0, 0.0, 0.0);
// this color should never be visible,
// only alpha is important
}
#endif
ENDGLSL
}
// 2nd pass: set depth to far plane such that
// we can use the normal depth test for the reflected geometry
Pass {
ZTest Always
Blend OneMinusDstAlpha DstAlpha
GLSLPROGRAM
uniform vec4 _Color;
// user-specified background color in the mirror
#ifdef VERTEX
void main()
{
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
gl_Position.z = gl_Position.w;
// the perspective division will divide gl_Position.z
// by gl_Position.w; thus, the depth is 1.0,
// which represents the far clipping plane
}
#endif
#ifdef FRAGMENT
void main()
{
gl_FragColor = vec4(_Color.rgb, 0.0);
// set alpha to 0.0 and
// the color to the user-specified background color
}
#endif
ENDGLSL
}
}
}

Rendering the Virtual Objects
[edit | edit source]Once we have cleared the depth buffer and marked the visible part of the mirror by setting the alpha component to 0, we can use the blend equation
Blend OneMinusDstAlpha DstAlpha
to render the virtual objects. Can't we? There is another situation in which we shouldn't render virtual objects and that's when they come out of the mirror! This can actually happen when real objects move into the reflecting surface. Water lilies and swimming objects are examples. We can avoid the rasterization of fragments of virtual objects that are outside the mirror by discarding them with the discard instruction (see Section “Cutaways”) if their coordinate in the local coordinate system of the mirror is positive. To this end, the vertex shader has to compute the vertex position in the local coordinate system of the mirror and therefore the shader requires the corresponding transformation matrix, which we have fortunately set in the script above. The complete shader code for the virtual objects is then:
Shader "GLSL shader for virtual objects in mirrors" {
Properties {
_Color ("Virtual Object's Color", Color) = (1, 1, 1, 1)
}
SubShader {
Tags { "Queue" = "Transparent+20" }
// render after mirror has been rendered
Pass {
Blend OneMinusDstAlpha DstAlpha
// when the framebuffer has alpha = 1, keep its color
// only write color where the framebuffer has alpha = 0
GLSLPROGRAM
// User-specified uniforms
uniform vec4 _Color;
uniform mat4 _WorldToMirror; // set by a script
// The following built-in uniforms
// are also defined in "UnityCG.glslinc",
// i.e. one could #include "UnityCG.glslinc"
uniform mat4 _Object2World; // model matrix
// Varying
varying vec4 positionInMirror;
#ifdef VERTEX
void main()
{
positionInMirror =
_WorldToMirror * (_Object2World * gl_Vertex);
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;;
}
#endif
#ifdef FRAGMENT
void main()
{
if (positionInMirror.y > 0.0)
// reflection comes out of mirror?
{
discard; // don't rasterize it
}
gl_FragColor = vec4(_Color.rgb, 0.0); // set alpha to 0.0
}
#endif
ENDGLSL
}
}
}
Note that the line
Tags { "Queue" = "Transparent+20" }
makes sure that the virtual objects are rendered after the mirror, which uses "Transparent+10". In this shader, the virtual objects are rasterized with a uniform, user-specified color in order to keep the shader as short as possible. In a complete solution, the shader would compute the lighting and texturing with the mirrored normal vector and mirrored positions of light sources. However, this is straightforward and very much dependent on the particular shaders that are employed for the real objects.
Limitations
[edit | edit source]There are several limitations of this approach which we haven't addressed. For example:
- multiple mirror planes (virtual objects of one mirror might appear in another mirror)
- multiple reflections in mirrors
- semitransparent virtual objects
- semitransparent mirrors
- reflection of light in mirrors
- uneven mirrors (e.g. with a normal map)
- uneven mirrors in the free version of Unity
- etc.
Summary
[edit | edit source]Congratulations! Well done. Two of the things we have looked at:
- How to render mirrors with a stencil buffer.
- How to render mirrors without a stencil buffer.
Further Reading
[edit | edit source]If you still want to know more
- about using the stencil buffer to render mirrors, you could read Section 9.3.1 of the SIGGRAPH '98 Course “Advanced Graphics Programming Techniques Using OpenGL” organized by Tom McReynolds, which is available online.
OpenGL ES 2.0 Pipeline
[edit | edit source]The OpenGL ES 2.0 pipeline is important for GLSL shaders in OpenGL ES 2.0 and WebGL. It is also very similar to the OpenGL 2.0 pipeline without many of the features that were deprecated in newer versions of OpenGL. Therefore, the OpenGL ES 2.0 pipeline is not only highly relevant for programmers of mobile graphics using OpenGL ES 2.0 and web-based 3D graphics using WebGL, but also a very good starting point to learn about desktop-based 3D graphics using OpenGL, including 3D graphics in game engines such as Blender, Unity and Torque 3D.
Parallelism in the OpenGL Pipeline
[edit | edit source]GPUs are highly parallel processors. This is the main reason for their performance. In fact, they implement two kinds of parallelism: vertical and horizontal parallelism:

- Vertical parallelism describes parallel processing at different stages of a pipeline. This concept was also crucial in the development of the assembly line at Ford Motor Company: many workers can work in parallel on rather simple tasks. This made mass production (and therefore mass consumption) possible. In the context of processing units in GPUs, the simple tasks correspond to less complex processing units, which save costs and power consumption.

- Horizontal parallelism describes the possibility to process work in multiple pipelines. This allows for even more parallelism than the vertical parallelism in a single pipeline. Again, the concept was also employed at Ford Motor Company and in many other industries. In the context of GPUs, horizontal parallelism of the graphics pipeline was an important feature to achieve the performance of modern GPUs.
The following diagram shows an illustration of vertical parallelism (processing in stages represented by boxes) and horizontal parallelism (multiple processing units for each stage represented by multiple arrows between boxes).
| Vertex Data | e.g. triangle meshes provided by 3D modeling tools | |||
| ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ | many vertices are processed in parallel | |||
| Vertex Shader | a small program in GLSL is applied to each vertex | |||
| ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ | ||||
| Primitive Assembly | setup of primitives, e.g. triangles, lines, and points | |||
| ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ | many primitives are processed in parallel | |||
| Rasterization | interpolation of data for all pixels covered by the primitive (e.g. triangle) | |||
| ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ | many fragments (corresponding to pixels) are processed in parallel | |||
| Fragment Shader | a small program in GLSL is applied to each fragment (i.e. covered pixel) | |||
| ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ | ||||
| Per-Fragment Operations | configurable operations on each fragment (i.e. covered pixel) | |||
| ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ | results of many fragments are written in parallel to the framebuffer | |||
| Framebuffer | array of pixels in which the computed fragment colors are stored | |||
In the following diagrams, there is only one arrow between any two stages. However, it should be understood that GPUs usually implement the graphics pipeline with massive horizontal parallelism. Only software implementations of OpenGL, e.g. Mesa 3D (see the Wikipedia entry), usually implement a single pipeline.
Programmable and Fixed-Function Stages
[edit | edit source]The pipelines of OpenGL ES 1.x and core OpenGL 1.x are configurable fixed-function pipelines, i.e. there is no possibility to include programs in these pipelines. In OpenGL (ES) 2.0 two stages (the vertex shader and the fragment shader stage) of the pipeline are programmable, i.e. small programs (shaders) written in GLSL are applied in these stages. In the following diagram, programmable stages are represented by green boxes, fixed-function stages are represented by gray boxes, and data is represented by blue boxes.
| Vertex Data | e.g. triangle meshes provided by 3D modeling tools | |||
| ↓ | ||||
| Vertex Shader | a small program in GLSL is applied to each vertex | |||
| ↓ | ||||
| Primitive Assembly | setup of primitives, e.g. triangles, lines, and points | |||
| ↓ | ||||
| Rasterization | interpolation of data (e.g. color) for all pixels covered by the primitive | |||
| ↓ | ||||
| Fragment Shader | a small program in GLSL is applied to each fragment (i.e. covered pixel) | |||
| ↓ | ||||
| Per-Fragment Operations | configurable operations on each fragment (i.e. covered pixel) | |||
| ↓ | ||||
| Framebuffer | array of pixels in which the computed fragment colors are stored | |||
The vertex shader and fragment shader stages are discussed in more detail in the platform-specific tutorials. The rasterization stage is discussed in Section “Rasterization” and the per-fragment operations in Section “Per-Fragment Operations”.
The primitive assembly stage mainly consists of clipping primitives to the view frustum (the part of space that is visible on the screen) and optional culling of front-facing and/or back-facing primitives. These possibilities are discussed in more detail in the platform-specific tutorials.
Data Flow
[edit | edit source]In order to program GLSL vertex and fragment shaders, it is important to understand the input and ouput of each shader. To this end, it is also useful to understand how data is communicated between all stages of the OpenGL pipeline. This is illustrated in the next diagram:
| Vertex Data | ||||
| ↓ | attributes (usually position, color, normal vector, and texture coordinates) | |||
| Vertex Shader | ← | uniforms (constants); (optionally texture data but not in most OpenGL ES 2.0 implementations) | ||
| ↓ | varyings (at vertices), vertex position, and point size | |||
| Primitive Assembly | ||||
| ↓ | varyings (at vertices), vertex position, and point size | |||
| Rasterization | ||||
| ↓ | varyings (now interpolated at pixels), fragment coordinates, point coordinates, front-facing flag | |||
| Fragment Shader | ← | uniforms (constants) and texture data (images) | ||
| ↓ | fragment color and fragment depth | |||
| Per-Fragment Operations | ||||
| ↓ | fragment color and fragment depth | |||
| Framebuffer | ||||
Attributes (or vertex attributes, or attribute variables) are defined based on the vertex data. The vertex position in an attribute is in object coordinates, i.e. this is the position as specified in a 3D modeling tool.
Uniforms (or uniform variables) have the same value for all vertex shaders and all fragment shaders that are executed when rendering a specific primitive (e.g. a triangle). However, they can be changed for other primitives. Typically, vertex transformations, specifications of light sources and materials, etc. are specified as uniforms.
Varyings (or varying variables) have to be consistently defined by the vertex shader and the fragment shader (i.e. the vertex shader has to define the same varying variables as the fragment shader). Typically, varyings are defined for colors, normal vectors, and/or texture coordinates.
Texture data include a uniform sampler, which specifies the texture sampling unit, which in turn specifies the texture image from which colors are fetched.
Other data is described in the tutorials for specific platforms.
Further Reading
[edit | edit source]The OpenGL ES 2.0 pipeline is defined in full detail in the “OpenGL ES 2.0.x Specification” and the “OpenGL ES Shading Language 1.0.x Specification” available at the “Khronos OpenGL ES API Registry”.
A more accessible description of the OpenGL ES 2.0 pipeline is given in Chapter 1 of the book “OpenGL ES 2.0 Programming Guide” by Aaftab Munshi, Dan Ginsburg and Dave Shreiner published by Addison-Wesley (see its web site).
Vertex Transformations
[edit | edit source]One of the most important tasks of the vertex shader and the following stages in the OpenGL (ES) 2.0 pipeline is the transformation of vertices of primitives (e.g. triangles) from the original coordinates (e.g. those specified in a 3D modeling tool) to screen coordinates. While programmable vertex shaders allow for many ways of transforming vertices, some transformations are performed in the fixed-function stages after the vertex shader. When programming a vertex shader, it is therefore particularly important to understand which transformations have to be performed in the vertex shader. These transformations are usually specified as uniform variables and applied to the incoming vertex positions and normal vectors by means of matrix-vector multiplications. While this is straightforward for points and directions, it is less straightforward for normal vectors as discussed in Section “Applying Matrix Transformations”.
Here, we will first present an overview of the coordinate systems and the transformations between them and then discuss individual transformations.

Overview: The Camera Analogy
[edit | edit source]It is useful to think of the whole process of transforming vertices in terms of a camera analogy as illustrated to the right. The steps and the corresponding vertex transformations are:
- positioning the model — modeling transformation
- positioning the camera — viewing transformation
- adjusting the zoom — projection transformation
- cropping the image — viewport transformation
The first three transformations are applied in the vertex shader. Then the perspective division (which might be considered part of the projection transformation) is automatically applied in the fixed-function stage after the vertex shader. The viewport transformation is also applied automatically in this fixed-function stage. While the transformations in the fixed-function stages cannot be modified, the other transformations can be replaced by other kinds of transformations than described here. It is, however, useful to know the conventional transformations since they allow to make best use of clipping and perspectively correct interpolation of varying variables.
The following overview shows the sequence of vertex transformations between various coordinate systems and includes the matrices that represent the transformations:
| object/model coordinates | input to the vertex shader, i.e. position in attributes | |||
| ↓ | modeling transformation: model matrix | |||
| world coordinates | ||||
| ↓ | viewing transformation: view matrix | |||
| view/eye coordinates | ||||
| ↓ | projection transformation: projection matrix | |||
| clip coordinates | output of the vertex shader, i.e. gl_Position
| |||
| ↓ | perspective division (by gl_Position.w)
| |||
| normalized device coordinates | ||||
| ↓ | viewport transformation | |||
| screen/window coordinates | gl_FragCoord in the fragment shader
| |||
Note that the modeling, viewing and projection transformation are applied in the vertex shader. The perspective division and the viewport transformation is applied in the fixed-function stage after the vertex shader. The next sections discuss all these transformations in detail.
Modeling Transformation
[edit | edit source]The modeling transformation specifies the transformation from object coordinates (also called model coordinates or local coordinates) to a common world coordinate system. Object coordinates are usually specific to each object or model and are often specified in 3D modeling tools. On the other hand, world coordinates are a common coordinate system for all objects of a scene, including light sources, 3D audio sources, etc. Since different objects have different object coordinate systems, the modeling transformations are also different; i.e., a different modeling transformation has to be applied to each object.
In effect, it 'pushes' the object away from the origin and optionally applies a rotation to it.
Structure of the Model Matrix
[edit | edit source]The modeling transformation can be represented by a 4×4 matrix, which we denote as the model matrix . Its structure is:
is a 3×3 matrix, which represents a linear transformation in 3D space. This includes any combination of rotations, scalings, and other less common linear transformations. t is a 3D vector, which represents a translation (i.e. displacement) in 3D space. combines and t in one handy 4×4 matrix. Mathematically spoken, the model matrix represents an affine transformation: a linear transformation together with a translation. In order to make this work, all three-dimensional points are represented by four-dimensional vectors with the fourth coordinate equal to 1:
When we multiply the matrix to such a point , the combination of the three-dimensional linear transformation and the translation shows up in the result:
Apart from the fourth coordinate (which is 1 as it should be for a point), the result is equal to
Accessing the Model Matrix in a Vertex Shader
[edit | edit source]The model matrix can be defined as a uniform variable such that it is available in a vertex shader. However, it is usually combined with the matrix of the viewing transformation to form the modelview matrix, which is then set as a uniform variable. In some versions of OpenGL (ES), a built-in uniform variable gl_ModelViewMatrix is available in the vertex shader. (See also Section “Applying Matrix Transformations”.)
Computing the Model Matrix
[edit | edit source]Strictly speaking, GLSL programmers don't have to worry about the computation of the model matrix since it is provided to the vertex shader in the form of a uniform variable. In fact, render engines, scene graphs, and game engines will usually provide the model matrix; thus, the programmer of a vertex shader doesn't have to worry about computing the model matrix. However, when developing applications in modern versions of OpenGL and OpenGL ES or in WebGL, the model matrix has to be computed. (OpenGL before version 3.2, the compatibility profiles of newer versions of OpenGL, and OpenGL ES 1.x provide functions to compute the model matrix.)
The model matrix is usually computed by combining 4×4 matrices of elementary transformations of objects, in particular translations, rotations, and scalings. Specifically, in the case of a hierarchical scene graph, the transformations of all parent groups (parent, grandparent etc.) of an object are combined to form the model matrix. Let's look at the most important elementary transformations and their matrices.
The 4×4 matrix representing the translation by a vector t is:
The 4×4 matrix representing the scaling by a factor along the axis, along the axis, and along the axis is:
The 4×4 matrix representing the rotation by an angle about a normalized axis is:
Special cases for rotations about particular axes can be easily derived. These are necessary, for example, to implement rotations for Euler angles. There are, however, multiple conventions for Euler angles, which won't be discussed here.
A normalized quaternion corresponds to a rotation by the angle . The direction of the rotation axis can be determined by normalizing the 3D vector .
Further elementary transformations exist, but are of less interest for the computation of the model matrix. The 4×4 matrices of these or other transformations are combined by matrix products. Suppose the matrices , , and are applied to an object in this particular order. ( might represent the transformation from object coordinates to the coordinate system of the parent group; the transformation from the parent group to the grandparent group; and the transformation from the grandparent group to world coordinates.) Then the combined matrix product is:
Note that the order of the matrix factors is important. Also note that this matrix product should be read from the right (where vectors are multiplied) to the left, i.e. is applied first while is applied last.

Viewing Transformation
[edit | edit source]The viewing transformation corresponds to placing and orienting the camera (or the eye of an observer). However, the best way to think of the viewing transformation is that it transforms the world coordinates into the view coordinate system (also: eye coordinate system) of a camera that is placed at the origin of the coordinate system, points to the negative axis and is put on the plane, i.e. the up-direction is given by the positive axis.
This step rotates the entire world towards the camera, which is always looking at a fixed position from the origin.
Accessing the View Matrix in a Vertex Shader
[edit | edit source]Similarly to the modeling transformation, the viewing transformation is represented by a 4×4 matrix, which is called view matrix . It can be defined as a uniform variable for the vertex shader; however, it is usually combined with the model matrix to form the modelview matrix . (In some versions of OpenGL (ES), a built-in uniform variable gl_ModelViewMatrix is available in the vertex shader.) Since the model matrix is applied first, the correct combination is:
(See also Section “Applying Matrix Transformations”.)
Computing the View Matrix
[edit | edit source]Analogously to the model matrix, GLSL programmers don't have to worry about the computation of the view matrix since it is provided to the vertex shader in the form of a uniform variable. However, when developing applications in modern versions of OpenGL and OpenGL ES or in WebGL, it is necessary to compute the view matrix. (In older versions of OpenGL this is usually achieved by a utility function called gluLookAt.)
Here, we briefly summarize how the view matrix can be computed from the position t of the camera, the view direction d, and a world-up vector k (all in world coordinates). The steps are straightforward:
1. Compute (in world coordinates) the direction z of the axis of the view coordinate system as the negative normalized d vector:
2. Compute (again in world coordinates) the direction x of the axis of the view coordinate system by:
3. Compute (still in world coordinates) the direction y of the axis of the view coordinate system:
Using x, y, z, and t, the inverse view matrix can be easily determined because this matrix maps the origin (0,0,0) to t and the unit vectors (1,0,0), (0,1,0) and (0,0,1) to x, y,, z. Thus, the latter vectors have to be in the columns of the matrix :
However, we require the matrix ; thus, we have to compute the inverse of the matrix . Note that the matrix has the form
with a 3×3 matrix and a 3D vector t. The inverse of such a matrix is:
Since in this particular case the matrix is orthogonal (because its column vectors are normalized and orthogonal to each other), the inverse of is just the transpose, i.e. the fourth step is to compute:
While the derivation of this result required some knowledge of linear algebra, the resulting computation only requires basic vector and matrix operations and can be easily programmed in any common programming language.

Projection Transformation and Perspective Division
[edit | edit source]First of all, the projection transformations determine the kind of projection, e.g. perspective or orthographic. Perspective projection corresponds to linear perspective with foreshortening, while orthographic projection is an orthogonal projection without foreshortening. The foreshortening is actually accomplished by the perspective division; however, all the parameters controlling the perspective projection are set in the projection transformation.
Technically spoken, the projection transformation transforms view coordinates to clip coordinates. (All parts of primitives that are outside the visible part of the scene are clipped away in clip coordinates.) It should be the last transformation that is applied to a vertex in a vertex shader before the vertex is returned in gl_Position. These clip coordinates are then transformed to normalized device coordinates by the perspective division, which is just a division of all coordinates by the fourth coordinate. (Normalized device coordinates are named as such because their values are between -1 and +1 for all points in the visible part of the scene.)
This step translates the 3d positions of object vertices to 2d positions on the screen.
Accessing the Projection Matrix in a Vertex Shader
[edit | edit source]Similarly to the modeling transformation and the viewing transformation, the projection transformation is represented by a 4×4 matrix, which is called projection matrix . It is usually defined as a uniform variable for the vertex shader. (In some versions of OpenGL (ES), a built-in uniform variable gl_Projection is available in the vertex shader; see also Section “Applying Matrix Transformations”.)
Computing the Projection Matrix
[edit | edit source]Analogously to the modelview matrix, GLSL programmers don't have to worry about the computation of the projection matrix. However, when developing applications in modern versions of OpenGL and OpenGL ES or in WebGL, it is necessary to compute the projection matrix. In older versions of OpenGL this is usually achieved with the functions gluPerspective, glFrustum, or glOrtho.
Here, we present the projection matrices for three cases:
- standard perspective projection (corresponds to
gluPerspective) - oblique perspective projection (corresponds to
glFrustum) - orthographic projection (corresponds to
glOrtho)
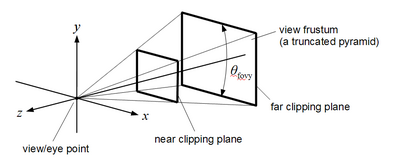

The standard perspective projection is characterized by
- an angle that specifies the field of view in direction as illustrated in the figure to the right,
- the distance to the near clipping plane and the distance to the far clipping plane as illustrated in the next figure,
- the aspect ratio of the width to the height of a centered rectangle on the near clipping plane.
Together with the view point and the clipping planes, this centered rectangle defines the view frustum, i.e. the region of the 3D space that is visible for the specific projection transformation. All primitives and all parts of primitives that are outside of the view frustum are clipped away. The near and front clipping planes are necessary because depth values are stored with a finite precision; thus, it is not possible to cover an infinitely large view frustum.
With the parameters , , , and , the projection matrix for the perspective projection is:

The oblique perspective projection is characterized by
- the same distances and to the clipping planes as in the case of the standard perspective projection,
- coordinates (right), (left), (top), and (bottom) as illustrated in the corresponding figure. These coordinates determine the position of the front rectangle of the view frustum; thus, more view frustums (e.g. off-center) can be specified than with the aspect ratio and the field-of-view angle .
Given the parameters , , , , , and , the projection matrix for the oblique perspective projection is:

An orthographic projection without foreshortening is illustrated in the figure to the right. The parameters are the same as in the case of the oblique perspective projection; however, the view frustum (more precisely, the view volume) is now simply a box instead of a truncated pyramid.
With the parameters , , , , , and , the projection matrix for the orthographic projection is:

Viewport Transformation
[edit | edit source]The projection transformation maps view coordinates to clip coordinates, which are then mapped to normalized device coordinates by the perspective division by the fourth component of the clip coordinates. In normalized device coordinates (ndc), the view volume is always a box centered around the origin with the coordinates inside the box between -1 and +1. This box is then mapped to screen coordinates (also called window coordinates) by the viewport transformation as illustrated in the corresponding figure. The parameters for this mapping are the coordinates and of the lower, left corner of the viewport (the rectangle of the screen that is rendered) and its width and height , as well as the depths and of the front and near clipping planes. (These depths are between 0 and 1). In OpenGL and OpenGL ES, these parameters are set with two functions:
glViewport(GLint , GLint ,
GLsizei , GLsizei );
glDepthRangef(GLclampf , GLclampf );
The matrix of the viewport transformation isn't very important since it is applied automatically in a fixed-function stage. However, here it is for the sake of completeness:
Further Reading
[edit | edit source]The conventional vertex transformations described here are defined in full detail in Section 2.12 of the “OpenGL 4.1 Compatibility Profile Specification” available at the Khronos OpenGL web site.
A more accessible description of the vertex transformations is given in Chapter 3 (on viewing) of the book “OpenGL Programming Guide” by Dave Shreiner published by Addison-Wesley. (An older edition is available online).
Vector and Matrix Operations
[edit | edit source]The syntax of GLSL is very similar to C (and therefore to C++ and Java); however, there are built-in data types and functions for floating-point vectors and matrices, which are specific to GLSL. These are discussed here. A full description of GLSL can be found in the literature in the “Further Reading” section.
Data Types
[edit | edit source]In GLSL, the types vec2, vec3, and vec4 represent 2D, 3D, and 4D floating-point vectors. (There are also types for integer and boolean vectors, which are not discussed here.) Vector variables are defined as you would expect if C, C++ or Java had these types:
vec2 a2DVector;
vec3 three_dimensional_vector;
vec4 vector4;
The data types for floating-point 2×2, 3×3, and 4×4 matrices are: mat2, mat3, and mat4:
mat2 m2x2;
mat3 linear_mapping;
mat4 trafo;
Precision Qualifiers
[edit | edit source]When declaring a floating-point variable (including vector and matrix variables), you can suggest a precision by using one of the precision qualifiers lowp, mediump, or highp, for example:
lowp vec4 color; // for colors, lowp is usually fine
mediump vec4 position; // for positions and texture coordinates, mediump is usually ok
highp vec4 astronomical_position; // for some positions and time, highp is necessary
//(precision of time measurement decreases over time
//and things get jumpy if they rely on absolute time since start of the application)
The idea is that lowp variables require less computation time and less storage (and therefore also less bandwidth) than mediump variables, and mediump variables require less time than highp variables. Thus, for best performance you should use the lowest precision that still gives satisfactory results. (There are only a few exceptions to this, for example accessing individual elements of a lowp vector can be slower than for a mediump vector because it requires additional decoding.)
Note that it is up to the compiler and driver to decide which precision is actually used; the precision qualifiers are only suggestions by the programmer. Also note that the range of lowp variables can be very limited (e.g. from -2.0 to 2.0), thus, lowp is most useful for colors but usually not for positions.
To define default precisions for all floating-point variables, you should use the precision command, for example:
precision mediump float;
This will use mediump if no explicit precision qualifier is specified for a floating-point variable. Without the command, the default precision for float is highp in an OpenGL or OpenGL ES vertex shader, highp in an OpenGL fragment shader, and undefined in an OpenGL ES fragment shader. (In Unity, however, the precision command is not available and the default precision is highp in a vertex shader and mediump in a fragment shader.)
Constructors
[edit | edit source]Vectors can be initialized and converted by constructors of the same name as the data type:
vec2 a = vec2(1.0, 2.0);
vec3 b = vec3(-1.0, 0.0, 0.0);
vec4 c = vec4(0.0, 0.0, 0.0, 1.0);
Note that some GLSL compilers will complain if integers are used to initialize floating-point vectors; thus, it is good practice to always include the decimal point.
One can also use one floating-point number in the constructor to set all components to the same value:
vec4 a = vec4(0.0); // = vec4(0.0, 0.0, 0.0, 0.0)
Casting a higher-dimensional vector to a lower-dimensional vector is also achieved with these constructors:
vec4 a = vec4(-1.0, 2.5, 4.0, 1.0);
vec3 b = vec3(a); // = vec3(-1.0, 2.5, 4.0)
vec2 c = vec2(b); // = vec2(-1.0, 2.5)
Casting a lower-dimensional vector to a higher-dimensional vector is achieved by supplying these constructors with the correct number of components:
vec2 a = vec2(0.1, 0.2);
vec3 b = vec3(0.0, a); // = vec3(0.0, 0.1, 0.2)
vec4 c = vec4(b, 1.0); // = vec4(0.0, 0.1, 0.2, 1.0)
Similarly, matrices can be initialized and constructed. Note that the values specified in a matrix constructor are consumed to fill the first column, then the second column, etc.:
mat3 m = mat3(
1.1, 2.1, 3.1, // first column (not row!)
1.2, 2.2, 3.2, // second column
1.3, 2.3, 3.3 // third column
);
mat3 id = mat3(1.0); // puts 1.0 on the diagonal
// all other components are 0.0
vec3 column0 = vec3(0.0, 1.0, 0.0);
vec3 column1 = vec3(1.0, 0.0, 0.0);
vec3 column2 = vec3(0.0, 0.0, 1.0);
mat3 n = mat3(column0, column1, column2); // sets columns of matrix n
If a larger matrix is constructed from a smaller matrix, the additional rows and columns are set to the values they would have in an identity matrix:
mat2 m2x2 = mat2(
1.1, 2.1,
1.2, 2.2
);
mat3 m3x3 = mat3(m2x2); // = mat3(
// 1.1, 2.1, 0.0,
// 1.2, 2.2, 0.0,
// 0.0, 0.0, 1.0)
mat2 mm2x2 = mat2(m3x3); // = m2x2
If a smaller matrix is constructed from a larger matrix, the top, left submatrix of the larger matrix is chosen, e.g. in the last line of the previous example.
Components
[edit | edit source]Components of vectors are accessed by array indexing with the []-operator (indexing starts with 0) or with the .-operator and the element names x, y, z, w or r, g, b, a or s, t, p, q:
vec4 v = vec4(1.1, 2.2, 3.3, 4.4);
float a = v[3]; // = 4.4
float b = v.w; // = 4.4
float c = v.a; // = 4.4
float d = v.q; // = 4.4
It is also possible to construct new vectors by extending the .-notation ("swizzling"):
vec4 v = vec4(1.1, 2.2, 3.3, 4.4);
vec3 a = v.xyz; // = vec3(1.1, 2.2, 3.3)
vec3 b = v.bgr; // = vec3(3.3, 2.2, 1.1)
vec2 c = v.tt; // = vec2(2.2, 2.2)
Matrices are considered to consist of column vectors, which are accessed by array indexing with the []-operator. Elements of the resulting (column) vector can be accessed as discussed above:
mat3 m = mat3(
1.1, 2.1, 3.1, // first column
1.2, 2.2, 3.2, // second column
1.3, 2.3, 3.3 // third column
);
vec3 column3 = m[2]; // = vec3(1.3, 2.3, 3.3)
float m20 = m[2][0]; // = 1.3
float m21 = m[2].y; // = 2.3
Operators
[edit | edit source]If the binary operators *, /, +, -, =, *=, /=, +=, -= are used between vectors of the same type, they just work component-wise:
vec3 a = vec3(1.0, 2.0, 3.0);
vec3 b = vec3(0.1, 0.2, 0.3);
vec3 c = a + b; // = vec3(1.1, 2.2, 3.3)
vec3 d = a * b; // = vec3(0.1, 0.4, 0.9)
Note in particular that a * b represents a component-wise product of two vectors, which is not often seen in linear algebra.
For matrices, these operators also work component-wise, except for the *-operator, which represents a matrix-matrix product, e.g.:
And in GLSL:
mat2 a = mat2(1., 2., 3., 4.);
mat2 b = mat2(10., 20., 30., 40.);
mat2 c = a * b; // = mat2(
// 1. * 10. + 3. * 20., 2. * 10. + 4. * 20.,
// 1. * 30. + 3. * 40., 2. * 30. + 4. * 40.)
For a component-wise matrix product, the built-in function matrixCompMult is provided.
The *-operator can also be used to multiply a floating-point value (i.e. a scalar) to all components of a vector or matrix (from left or right):
vec3 a = vec3(1.0, 2.0, 3.0);
mat3 m = mat3(1.0);
float s = 10.0;
vec3 b = s * a; // vec3(10.0, 20.0, 30.0)
vec3 c = a * s; // vec3(10.0, 20.0, 30.0)
mat3 m2 = s * m; // = mat3(10.0)
mat3 m3 = m * s; // = mat3(10.0)
Furthermore, the *-operator can be used for matrix-vector products of the corresponding dimension, e.g.:
And in GLSL:
vec2 v = vec2(10., 20.);
mat2 m = mat2(1., 2., 3., 4.);
vec2 w = m * v; // = vec2(1. * 10. + 3. * 20., 2. * 10. + 4. * 20.)
Note that the vector has to be multiplied to the matrix from the right.
If a vector is multiplied to a matrix from the left, the result corresponds to multiplying a row vector from the left to the matrix. This corresponds to multiplying a column vector to the transposed matrix from the right:
In components:
Thus, multiplying a vector from the left to a matrix corresponds to multiplying it from the right to the transposed matrix:
vec2 v = vec2(10., 20.);
mat2 m = mat2(1., 2., 3., 4.);
vec2 w = v * m; // = vec2(1. * 10. + 2. * 20., 3. * 10. + 4. * 20.)
Since there is no built-in function to compute a transposed matrix, this technique is extremely useful: whenever a vector should be multiplied with a transposed matrix, one can just multiply it from the left to the original matrix. Several applications of this technique are described in Section “Applying Matrix Transformations”.
Built-In Vector and Matrix Functions
[edit | edit source]Component-Wise Functions
[edit | edit source]As mentioned, the function
TYPE matrixCompMult(TYPE a, TYPE b) // component-wise matrix product
computes a component-wise product for the matrix types mat2, mat3 and mat4, which are denoted as TYPE.
The following functions work component-wise for variables of type float, vec2, vec3 and vec4, which are denoted as TYPE:
TYPE min(TYPE a, TYPE b) // returns a if a < b, b otherwise
TYPE min(TYPE a, float b) // returns a if a < b, b otherwise
TYPE max(TYPE a, TYPE b) // returns a if a > b, b otherwise
TYPE max(TYPE a, float b) // returns a if a > b, b otherwise
TYPE clamp(TYPE a, TYPE minVal, TYPE maxVal)
// = min(max(a, minVal), maxVal)
TYPE clamp(TYPE a, float minVal, float maxVal)
// = min(max(a, minVal), maxVal)
TYPE mix(TYPE a, TYPE b, TYPE wb) // = a * (TYPE(1.0) - wb) + b * wb
TYPE mix(TYPE a, TYPE b, float wb) // = a * TYPE(1.0 - wb) + b * TYPE(wb)
There are more built-in functions, which also work component-wise but are less useful for vectors, e.g., abs, sign, floor, ceil, fract, mod, step, smoothstep, sqrt, inversesqrt, pow, exp, exp2, log, log2, radians (converts degrees to radians), degrees (converts radians to degrees), sin, cos, tan, asin, acos, atan (with one argument and with two arguments for signed numerator and signed denominator), lessThan, lessThanEqual, greaterThan, greaterThanEqual, equal, notEqual, and not.
Geometric Functions
[edit | edit source]The following functions are particular useful for vector operations. TYPE is any of: float, vec2, vec3 and vec4 (only one of them per line).
vec3 cross(vec3 a, vec3 b) // = vec3(a[1] * b[2] - a[2] * b[1],
// a[2] * b[0] - a[0] * b[2],
// a[0] * b[1] - a[1] * b[0])
float dot(TYPE a, TYPE b) // = a[0] * b[0] + a[1] * b[1] + ...
float length(TYPE a) // = sqrt(dot(a, a))
float distance(TYPE a, TYPE b) // = length(a - b)
TYPE normalize(TYPE a) // = a / length(a)
TYPE faceforward(TYPE n, TYPE i, TYPE nRef)
// returns n if dot(nRef, i) < 0, -n otherwise
TYPE reflect(TYPE i, TYPE n) // = i - 2. * dot(n, i) * n
// this computes the reflection of vector 'i'
// at a plane of normalized(!) normal vector 'n'
Functions for Physics
[edit | edit source]The function
TYPE refract(TYPE i, TYPE n, float r)
computes the direction of a refracted ray if i specifies the normalized(!) direction of the incoming ray and n specifies the normalized(!) normal vector of the interface of two optical media (e.g. air and water). The vector n should point to the side from where i is coming, i.e. the dot product of n and i should be negative. The floating-point number r is the ratio of the refractive index of the medium from where the ray comes to the refractive index of the medium on the other side of the surface. Thus, if a ray comes from air (refractive index about 1.0) and hits the surface of water (refractive index 1.33), then the ratio r is 1.0 / 1.33 = 0.75. The computation of the function is:
float d = 1.0 - r * r * (1.0 - dot(n, i) * dot(n, i));
if (d < 0.0) return TYPE(0.0); // total internal reflection
return r * i - (r * dot(n, i) + sqrt(d)) * n;
As the code shows, the function returns a vector of length 0 in the case of total internal reflection (see the entry in Wikipedia), i.e. if the ray does not pass the interface between the two materials.
Further Reading
[edit | edit source]All details of GLSL for OpenGL are specified in the “OpenGL Shading Language 4.10.6 Specification” available at the Khronos OpenGL web site.
More accessible descriptions of the OpenGL shading language for OpenGL are given in recent editions of many books about OpenGL, e.g. in Chapter 15 of the “OpenGL Programming Guide: The Official Guide to Learning OpenGL, Versions 3.0 and 3.1” (7th ed.) by Dave Shreiner published 2009 by Addison-Wesley.
All details of GLSL for OpenGL ES 2.0 are specified in the “OpenGL ES Shading Language 1.0.17 Specification” available at the “Khronos OpenGL ES API Registry”.
A more accessible description of the OpenGL ES shading language is given in Chapter 5 and Appendix B of the book “OpenGL ES 2.0 Programming Guide” by Aaftab Munshi, Dan Ginsburg and Dave Shreiner published by Addison-Wesley (see its web site).
Applying Matrix Transformations
[edit | edit source]Applying the conventional vertex transformations (see Section “Vertex Transformations”) or any other transformations that are represented by matrices in shaders is usually accomplished by specifying the corresponding matrix in a uniform variable of the shader and then multiplying the matrix with a vector. There are, however, some differences in the details. Here, we discuss the transformation of points (i.e. 4D vectors with a 4th coordinates equal to 1), the transformation of directions (i.e. vectors in the strict sense: 3D vectors or 4D vectors with a 4th coordinate equal to 0), and the transformation of surface normal vectors (i.e. vectors that specify a direction that is orthogonal to a plane).
This section assumes some knowledge of the syntax of GLSL as described in Section “Vector and Matrix Operations”.
Transforming Points
[edit | edit source]For points, transformations are usually represented by 4×4 matrices since they might include a translation by a 3D vector t in the 4th column:
(Projection matrices will also include additional values unequal to 0 in the last row.)
Three-dimensional points are represented by four-dimensional vectors with the 4th coordinate equal to 1:
In order to apply the transformation, the matrix is multiplied with the vector :
The GLSL code to apply a 4×4 matrix to a point represented by a 4D vector is straightforward:
mat4 matrix;
vec4 point;
vec4 transformed_point = matrix * point;
Transforming Directions
[edit | edit source]Directions in three dimensions are represented either by a 3D vector or by a 4D vector with 0 as the fourth coordinate. (One can think of them as points at infinity; similar to a point at the horizon of which we cannot tell the position in space but only the direction in which to find it.)
In the case of a 3D vector, we can either transform it by multiplying it with a 3×3 matrix:
mat3 matrix;
vec3 direction;
vec3 transformed_direction = matrix * direction;
or with a 4×4 matrix, if we convert the 3D vector to a 4D vector with a 4th coordinate equal to 0:
mat4 matrix;
vec3 direction;
vec3 transformed_direction = vec3(matrix * vec4(direction, 0.0));
Alternatively, the 4×4 matrix can also be converted to a 3×3 matrix.
On the other hand, a 4D vector can be multiplied directly with a 4×4 matrix. It can also be converted to a 3D vector in order to multiply it with a 3×3 matrix:
mat3 matrix;
vec4 direction; // 4th component is 0
vec4 transformed_direction = vec4(matrix * vec3(direction), 0.0);
Transforming Normal Vectors
[edit | edit source]Similarly to directions, surface normal vectors (or “normal vectors” for short) are represented by 3D vectors or 4D vectors with 0 as the 4th component. However, they transform differently. (The mathematical reason is that they represent something that is called a covector, covariant vector, one-form, or linear functional.)
To understand the transformation of normal vectors, consider the main feature of a surface normal vector: it is orthogonal to a surface. Of course, this feature should still be true under transformations, i.e. the transformed normal vector should be orthogonal to the transformed surface. If the surface is being represented locally by a tangent vector, this feature requires that a transformed normal vector is orthogonal to a transformed direction vector if the original normal vector is orthogonal to the original direction vector.
Mathematically spoken, a normal vector n is orthogonal to a direction vector v if their dot product is 0. It turns out that if v is transformed by a 3×3 matrix , the normal vector has to be transformed by the transposed inverse of : . We can easily test this by checking the dot product of the transformed normal vector n and the transformed direction vector v:
In the first step we have used = , then = , then , then (i.e. the identity matrix).
The calculation shows that the dot product of the transformed vectors is in fact the same as the dot product of the original vectors; thus, the transformed vectors are orthogonal if and only if the original vectors are orthogonal. Just the way it should be.
Thus, in order to transform normal vectors in GLSL, the transposed inverse matrix is often specified as a uniform variable (together with the original matrix for the transformation of directions and points) and applied as any other transformation:
mat3 matrix_inverse_transpose;
vec3 normal;
vec3 transformed_normal = matrix_inverse_transpose * normal;
In the case of a 4×4 matrix, the normal vector can be cast to a 4D vector by appending 0:
mat4 matrix_inverse_transpose;
vec3 normal;
vec3 transformed_normal = vec3(matrix_inverse_transpose * vec4(normal, 0.0));
Alternatively, the matrix can be cast to a 3×3 matrix.
If the inverse matrix is known, the normal vector can be multiplied from the left to apply the transposed inverse matrix. In general, multiplying a transposed matrix with a vector can be easily expressed by putting the vector to the left of the matrix. The reason is that a vector-matrix product makes only sense for row vectors (i.e. transposed column vectors) and corresponds to a matrix-vector product of the transposed matrix with the corresponding column vector:
Since GLSL makes no distinction between column and row vectors, the result is just a vector.
Thus, in order to multiply a normal vector with the transposed inverse matrix, we can multiply it from the left to the inverse matrix:
mat3 matrix_inverse;
vec3 normal;
vec3 transformed_normal = normal * matrix_inverse;
In the case of multiplying a 4×4 matrix to a 4D normal vector (from the left or the right), it should be made sure that the 4th component of the resulting vector is 0. In fact, in several cases it is necessary to discard the computed 4th component (for example by casting the result to a 3D vector):
mat4 matrix_inverse;
vec4 normal;
vec4 transformed_normal = vec4(vec3(normal * matrix_inverse), 0.0);
Note that any normalization of the normal vector to unit length is not preserved by this transformation. Thus, normal vectors are often normalized to unit length after the transformation (e.g. with the built-in GLSL function normalize).
Transforming Normal Vectors with an Orthogonal Matrix
[edit | edit source]A special case arises when the transformation matrix is orthogonal. In this case, the inverse of is the transposed matrix; thus, the transposed of the inverse of is the twice transposed matrix, which is the original matrix, i.e. for a orthogonal matrix :
Thus, in the case of orthogonal matrices, normal vectors are transformed with the same matrix as directions and points:
mat3 matrix; // orthogonal matrix
vec3 normal;
vec3 transformed_normal = matrix * normal;
Transforming Points with the Inverse Matrix
[edit | edit source]Sometimes it is necessary to apply the inverse transformation. In most cases, the best solution is to define another uniform variable for the inverse matrix and set the inverse matrix in the main application. The shader can then apply the inverse matrix like any other matrix. This is by far more efficient than computing the inverse in the shader.
There is, however, a special case: If the matrix is of the form presented above (i.e. the 4th row is (0,0,0,1)):
with an orthogonal 3×3 matrix (i.e. the row (or column) vectors of are normalized and orthogonal to each other; for example, this is usually the case for the view transformation, see Section “Vertex Transformations”), then the inverse matrix is given by (because for an orthogonal matrix ):
For the multiplication with a point that is represented by the 4D vector with the 3D vector p we get:
Note that the vector t is just the 4th column of the matrix , which can be conveniently accessed in GLSL:
mat4 matrix;
vec4 last_column = matrix[3]; // indices start with 0 in GLSL
As mentioned above, multiplying a transposed matrix with a vector can be easily expressed by putting the vector to the left of the matrix because a vector-matrix product makes only sense for row vectors (i.e. transposed column vectors) and corresponds to a matrix-vector product of the transposed matrix with the corresponding column vector:
Using these features of GLSL, the term (p - t) is easily and efficiently implemented as follows (note that the 4th component of the result has to be set to 1 separately):
mat4 matrix; // upper, left 3x3 matrix is orthogonal;
// 4th row is (0,0,0,1)
vec4 point; // 4th component is 1
vec4 point_transformed_with_inverse = vec4(vec3((point - matrix[3]) * matrix), 1.0);
Transforming Directions with the Inverse Matrix
[edit | edit source]As in the case of points, the best way to transform a direction with the inverse matrix is usually to compute the inverse matrix in the main application and communicate it to a shader via another uniform variable.
The exception is an orthogonal 3×3 matrix (i.e. all rows (or columns) are normalized and orthogonal to each other) or a 4×4 matrix of the form
where is an orthogonal 3×3 matrix. In these cases, the inverse matrix is equal to the transposed matrix .
As discussed above, the best way in GLSL to multiply a vector with the transposed matrix is to multiply it from the left to the original matrix because this is interpreted as a product of a row vector with the original matrix, which corresponds to the product of the transposed matrix with the column vector:
Thus, the transformation with the transposed matrix (i.e. the inverse in case of a orthogonal matrix) is written as:
mat4 matrix; // upper, left 3x3 matrix is orthogonal
vec4 direction; // 4th component is 0
vec4 direction_transformed_with_inverse = vec4(vec3(direction * matrix), 0.0);
Note that the 4th component of the result has to be set to 0 separately since the 4th component of direction * matrix is not meaningful for the transformation of directions. (It is, however, meaningful for the transformation of plane equations, which are not discussed here.)
The versions for 3x3 matrices and 3D vectors only require different cast operations between 3D and 4D vectors.
Transforming Normal Vectors with the Inverse Transformation
[edit | edit source]Suppose the inverse matrix is available, but the transformation corresponding to is required. Moreover, we want to apply this transformation to a normal vector. In this case, we can just apply the transpose of the inverse by multiplying the normal vector from the left to the inverse matrix (as discussed above):
mat4 matrix_inverse;
vec3 normal;
vec3 transformed_normal = vec3(vec4(normal, 0.0) * matrix_inverse);
(or by casting the matrix).
Built-In Matrix Transformations
[edit | edit source]Some frameworks (in particular the OpenGL compatibility profile but neither the OpenGL core profile nor OpenGL ES 2.x) provide several built-in uniforms to access certain vertex transformations in GLSL shaders. They should not be declared, but here are the declarations to specify their types:
uniform mat4 gl_ModelViewMatrix;
uniform mat4 gl_ProjectionMatrix;
uniform mat4 gl_ModelViewProjectionMatrix;
uniform mat4 gl_TextureMatrix[gl_MaxTextureCoords];
uniform mat3 gl_NormalMatrix; // transpose of the inverse of the
// upper left 3x3 matrix of gl_ModelViewMatrix
uniform mat4 gl_ModelViewMatrixInverse;
uniform mat4 gl_ProjectionMatrixInverse;
uniform mat4 gl_ModelViewProjectionMatrixInverse;
uniform mat4 gl_TextureMatrixInverse[gl_MaxTextureCoords];
uniform mat4 gl_ModelViewMatrixTranspose;
uniform mat4 gl_ProjectionMatrixTranspose;
uniform mat4 gl_ModelViewProjectionMatrixTranspose;
uniform mat4 gl_TextureMatrixTranspose[gl_MaxTextureCoords];
uniform mat4 gl_ModelViewMatrixInverseTranspose;
uniform mat4 gl_ProjectionMatrixInverseTranspose;
uniform mat4 gl_ModelViewProjectionMatrixInverseTranspose;
uniform mat4 gl_TextureMatrixInverseTranspose[gl_MaxTextureCoords];
Further Reading
[edit | edit source]The transformation of normal vectors is described in Section 2.12.2 of the “OpenGL 4.1 Compatibility Profile Specification” available at the Khronos OpenGL web site.
A more accessible description of the transformation of normal vectors is given in Appendix E of the free HTML version of the “OpenGL Programming Guide” available online.
The built-in uniforms of matrix transformations are described in Section 7.4.1 of the “OpenGL Shading Language 4.10.6 Specification” available at the Khronos OpenGL web site.
Rasterization
[edit | edit source]Rasterization is the stage of the OpenGL (ES) 2.0 pipeline that determines the pixels covered by a primitive (e.g. a triangle) and interpolates the output variables of the vertex shader (i.e. varying variables and depth) for each covered pixel. These interpolated varying variables and the interpolated depth are then given to the fragment shader. (In a wider sense, the term “rasterization” also includes the execution of the fragment shader and the per-fragment operations.)
Usually, it is not necessary for GLSL programmers to know more about the rasterization stage than described in the previous paragraph. However, it is useful to know some details in order to understand features such as perspectively correct interpolation and the role of the fourth component of the vertex position that is computed by the vertex shader. For some advanced algorithms in computer graphics it is also necessary to know some details of the rasterization process.
The main two parts of the rasterization are:
- Determining the pixels that are covered by a primitive (e.g. a triangle)
- Linear interpolation of varying variables and depth for all covered pixels

Determining Covered Pixels
[edit | edit source]In OpenGL (ES), a pixel of the framebuffer is defined as being covered by a primitive if the center of the pixel is covered by the primitive as illustrated in the diagram to the right.
There are certain rules for cases when the center of a pixel is exactly on the boundary of a primitive. These rules make sure that two adjacent triangles (i.e. triangles that share an edge) never share any pixels (unless they actually overlap) and never miss any pixels along the edge; i.e. each pixel along the edge between two adjacent triangles is covered by either triangle but not by both. This is important to avoid holes and (in case of semitransparent triangles) multiple rasterizations of the same pixel. The rules are, however, specific to implementations of GPUs; thus, they won't be discussed here.

Linear Interpolation of Varying Variables
[edit | edit source]Once all the covered pixels are determined, varying variables are interpolated for each pixel. For simplicity, we will only discuss the case of a triangle. (A line works like a triangle with two vertices at the same position.)
For each triangle, the vertex shader computes the positions of the three vertices. In the diagram to the right, these positions are labeled as , , and . The vertex shader also computes values of varying variables at each vertex. We denote one of them as , , and . Note that these values refer to the same varying variable computed at different vertices. The position of the center of the pixel for which we want to interpolate the varying variables is labeled by in the diagram.
We want to compute a new interpolated value at the pixel center from the values , , and at the three vertices. There are several methods to do this. One is using barycentric coordinates , , and , which are computed this way:
The triangle areas , , , and are also shown in the diagram. In three dimensions (or two dimensions with an additional third dimension) the area of a triangle between three points , , , can be computed as one half of the length of a cross product:
With the barycentric coordinates , , and , the interpolation of at from the values , , and at the three vertices is easy:
This way, all varying variables can be linearly interpolated for all covered pixels.

Perspectively Correct Interpolation of Varying Variables
[edit | edit source]The interpolation described in the previous section can result in certain distortions if applied to scenes that use perspective projection. For the perspectively correct interpolation the distance to the view point is placed in the fourth component of the three vertex positions (, , and ) and the following equation is used for the interpolation:
Thus, the fourth component of the position of the vertices is important for perspectively correct interpolation of varying variables. Therefore, it is also important that the perspective division (which sets this fourth component to 1) is not performed in the vertex shader, otherwise the interpolation will be incorrect in the case of perspective projections. (Moreover, clipping fails in some cases.)
It should be noted that actual OpenGL implementations are unlikely to implement exactly the same procedure because there are more efficient techniques. However, all perspectively correct linear interpolation methods result in the same interpolated values.
Further Reading
[edit | edit source]All details about the rasterization of OpenGL ES are defined in full detail in Chapter 3 of the “OpenGL ES 2.0.x Specification” available at the “Khronos OpenGL ES API Registry”.
Per-Fragment Operations
[edit | edit source]The per-fragment operations are part of the OpenGL (ES) 2.0 pipeline and consist of a series of tests and operations that can modify the fragment color generated by the fragment shader before it is written to the corresponding pixel in the framebuffer. If any of the tests fails, the fragment will be discarded. (An exception to this rule is the stencil test, which can be configured to change the stencil value of the pixel even if the fragment failed the stencil and/or depth test.)
Overview
[edit | edit source]In the overview of the per-fragment operations, blue boxes represent data and gray boxes represent configurable per-fragment operations.
| Fragment Data (Color and Depth) | output of the fragment shader | |||
| ↓ | ||||
| Pixel Ownership Test | not customizable by applications | |||
| ↓ | ||||
| Scissor Test | fails if fragment is outside of a specified (scissor) rectangle | |||
| ↓ | ||||
| Alpha Test | only in OpenGL, not in OpenGL ES 2.x; outcome depends on alpha value (opacity) of the fragment, a reference alpha value and the configured alpha test | |||
| ↓ | ||||
| Stencil Test | outcome depends on value in stencil buffer at corresponding pixel and the configured stencil test | |||
| ↓ | ||||
| Depth Test | outcome depends on depth of fragment, depth in depth buffer at the corresponding pixel and the configured depth test | |||
| ↓ | ||||
| Blending | outcome depends on fragment color (including its opacity), color in framebuffer at corresponding pixel and configured blend equation | |||
| ↓ | ||||
| Dithering | usually not customizable by applications | |||
| ↓ | ||||
| Logical Operations | only in OpenGL, not in OpenGL ES 2.x; outcome depends on color of fragment, color in framebuffer at corresponding pixel and configured logical (bitwise) operation | |||
| ↓ | ||||
| Framebuffer (Color, Depth and Stencil Value) | writing to the framebuffer can be disabled for individual channels | |||
Specific Per-Fragment Operations
[edit | edit source]Some of the per-fragment operations are particularly important because they have established applications:
- The depth test is used to render opaque primitives (e.g. triangles) with correct occlusions. This is done by comparing the depth of a fragment to the depth of the frontmost previously rendered fragment, which is stored in the depth buffer. If the fragment is farther away, then the depth test fails and the fragment is discarded. Otherwise the fragment is the new frontmost fragment and its depth is stored in the depth buffer.
- Blending is used to render semitransparent primitives (glass, fire, flares, etc.) by blending (i.e. compositing) the color of the fragment with the color that is already stored in the framebuffer. This is usually combined with disabling writing to the depth buffer in order to avoid that semitransparent primitives occlude other primitives.
- The stencil test is often used to restrict rendering to certain regions of the screen, e.g. a mirror, a window or a more general “portal” in the 3D scene. It also has more advanced uses for some algorithms, e.g. shadow volumes.
More details about specific per-fragment operations can be found in the platform-specific tutorials because it depends on the platform, how the operations are configured.
Note on the Order of Per-Fragment Operations
[edit | edit source]While the specification of OpenGL imposes a certain order of the per-fragment operations, GPUs can change the order of these operations as long as this doesn't change the result. In fact, GPUs will perform many of the tests even before the fragment shader is executed whenever this is possible. In this case the fragment shader is not executed for a fragment that has failed one of the test. (One example is the so-called “early depth test.”) This can result in considerable performance gains.
Programmability of Per-Fragment Operations
[edit | edit source]Per-fragment operations are usually configurable but not programmable, i.e. the various tests can be configured in certain ways but you cannot write a program to compute the tests. However, this is changing. For example, OpenGL ES 2.0 offers no alpha test because the same functionality can be achieved by a conditional discard operation in a fragment shader, which is effectively a programmable alpha test. Another example is the (multi-vendor) OpenGL ES extension GL_EXT_shader_framebuffer_fetch, which offers programmable blending. (This extension is supported on most (if not all) iOS 6 devices. In beta versions of iOS 6, the extension was available as GL_APPLE_shader_framebuffer_fetch. On devices with Nvidia's Tegra chip, the similar extension GL_NV_shader_framebuffer_fetch is often available.)
Further Reading
[edit | edit source]The per-fragment operations of OpenGL ES 2.0 are defined in full detail in Chapter 4 of the “OpenGL ES 2.0.x Specification” available at the “Khronos OpenGL ES API Registry”.
A more accessible description is given in Chapter 11 of the book “OpenGL ES 2.0 Programming Guide” by Aaftab Munshi, Dan Ginsburg and Dave Shreiner published by Addison-Wesley (see its web site).





















































![{\displaystyle \mathrm {M} _{{\text{surface}}\to {\text{world}}}=\left[{\begin{matrix}T_{x}&B_{x}&N_{x}\\T_{y}&B_{y}&N_{y}\\T_{z}&B_{z}&N_{z}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcbbe6f98b198dcccb4813c8859bce07721b98a5)


![{\displaystyle \mathrm {M} _{{\text{surface}}\to {\text{object}}}=\left[{\begin{matrix}T_{x}&B_{x}&N_{x}\\T_{y}&B_{y}&N_{y}\\T_{z}&B_{z}&N_{z}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/242e02fde6767d2ead326f94be91251497b69a21)


































































































![{\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74f8aaab560e5cb2f74f328599b57b54638f29f6)
![{\displaystyle {\text{ with }}\mathrm {A} =\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcff6fb39a87563940e5b11f2cd33c100e98d8de)
![{\displaystyle {\text{ and }}\mathbf {t} =\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1762d98b5711974550f359f7b06264db7c931360)

![{\displaystyle P=\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa4c63dd467c6eb272d3b11d2dcb27c641be56bf)

![{\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}\;P=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13d11dfa872a62f11d49f0b7594bea2e57f36ab1)
![{\displaystyle =\left[{\begin{matrix}a_{1,1}p_{1}+a_{1,2}p_{2}+a_{1,3}p_{3}+t_{1}\\a_{2,1}p_{1}+a_{2,2}p_{2}+a_{2,3}p_{3}+t_{2}\\a_{3,1}p_{1}+a_{3,2}p_{2}+a_{3,3}p_{3}+t_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f96ff85224b8f3fb35ccd73c31b54bd69cca25d)
![{\displaystyle \mathrm {A} \left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\end{matrix}}\right]+\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff6335e75528b3f090325320d6db5f829863e54e)

![{\displaystyle \mathrm {M} _{\text{translation}}=\left[{\begin{matrix}1&0&0&t_{1}\\0&1&0&t_{2}\\0&0&1&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9ccb86cb24fb7ce0bf772f83efbb7391c312146)



![{\displaystyle \mathrm {M} _{\text{scaling}}=\left[{\begin{matrix}s_{x}&0&0&0\\0&s_{y}&0&0\\0&0&s_{z}&0\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b366a6c227cafdd36ec11f98948bc514b42ef014)
![{\displaystyle \mathrm {M} _{\text{rotation}}=\left[{\begin{matrix}(1-\cos \alpha )x\,x+\cos \alpha &(1-\cos \alpha )x\,y-z\sin \alpha &(1-\cos \alpha )z\,x+y\sin \alpha &0\\(1-\cos \alpha )x\,y+z\sin \alpha &(1-\cos \alpha )y\,y+\cos \alpha &(1-\cos \alpha )y\,z-x\sin \alpha &0\\(1-\cos \alpha )z\,x-y\sin \alpha &(1-\cos \alpha )y\,z+x\sin \alpha &(1-\cos \alpha )z\,z+\cos \alpha &0\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68f40eec0dda33d6ffef4c0c25b0586470d62fef)













![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}x_{1}&y_{1}&z_{1}&t_{1}\\x_{2}&y_{2}&z_{2}&t_{2}\\x_{3}&y_{3}&z_{3}&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e00ec26b5506a084ce548aef7c370c0097ed34a)

![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}\mathrm {R} &\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcd0a52a1646832fca2af268dd812f7a7cbbc5ca)

![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}^{-1}=\mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{-1}&-\mathrm {R} ^{-1}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24280cf60fc5e0c97a0623ca0dea8a080d80b017)
![{\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{T}&-\mathrm {R} ^{T}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67a2e4ff6d60e39d428d0cac5ab3266f5c1b586)
![{\displaystyle {\text{with }}\mathrm {R} =\left[{\begin{matrix}x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2}\\x_{3}&y_{3}&z_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba6f143978631c3e9f3414b755a11e4429c16ee3)






![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {d}{a}}&0&0&0\\0&d&0&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43afae7ea0ce408c5a1a479a265177d988a0fb1c)





![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2n}{r-l}}&0&{\frac {r+l}{r-l}}&0\\0&{\frac {2n}{t-b}}&{\frac {t+b}{t-b}}&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43a44af0b15159b3378c0d628f98e88f6fa82c86)
![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2}{r-l}}&0&0&-{\frac {r+l}{r-l}}\\0&{\frac {2}{t-b}}&0&-{\frac {t+b}{t-b}}\\0&0&{\frac {-2}{f-n}}&-{\frac {f+n}{f-n}}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7345d54b1caa48a201493b48d21f86f2a2321ac)




![{\displaystyle \mathrm {M} _{\text{viewport}}=\left[{\begin{matrix}{\frac {w_{s}}{2}}&0&0&s_{x}+{\frac {w_{s}}{2}}\\0&{\frac {h_{s}}{2}}&0&s_{y}+{\frac {h_{s}}{2}}\\0&0&{\frac {f_{s}-n_{s}}{2}}&{\frac {n_{s}+f_{s}}{2}}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/449547f85546e323694f1165ef4632c6991b0586)
![{\displaystyle \mathrm {A} \mathrm {B} =\left[{\begin{matrix}a_{1,1}&a_{1,2}\\a_{2,1}&a_{2,2}\end{matrix}}\right]\left[{\begin{matrix}b_{1,1}&b_{1,2}\\b_{2,1}&b_{2,2}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1b0245d0eb208e6f13ff80b33484bbdc318f78c)
![{\displaystyle =\left[{\begin{matrix}a_{1,1}b_{1,1}+a_{1,2}b_{2,1}&a_{1,1}b_{1,2}+a_{1,2}b_{2,2}\\a_{2,1}b_{1,1}+a_{2,2}b_{2,1}&a_{2,1}b_{1,2}+a_{2,2}b_{2,2}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/964e26788c3f30abf0b05126bf7b8f0a19c0947b)
![{\displaystyle \mathrm {M} \mathbf {v} =\left[{\begin{matrix}m_{1,1}&m_{1,2}\\m_{2,1}&m_{2,2}\end{matrix}}\right]\left[{\begin{matrix}v_{1}\\v_{2}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cb45f7685fe7bce547a72f75e5e1fd12deda162)
![{\displaystyle =\left[{\begin{matrix}m_{1,1}v_{1}+m_{1,2}v_{2}\\m_{2,1}v_{1}+m_{2,2}v_{2}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32484e275b52ba45d1ba228913046a2c12ddec8a)

![{\displaystyle \mathbf {v} ^{T}\mathrm {M} =\left[{\begin{matrix}v_{1}&v_{2}\end{matrix}}\right]\left[{\begin{matrix}m_{1,1}&m_{1,2}\\m_{2,1}&m_{2,2}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cb7e02a6abff3e8a9546dbde53de4daf014884d)
![{\displaystyle =\left[{\begin{matrix}v_{1}m_{1,1}+v_{2}m_{2,1}&v_{1}m_{1,2}+v_{2}m_{2,2}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e82fd9a167de490a5035b312d4c5b85757eed707)
![{\displaystyle =\left(\left[{\begin{matrix}m_{1,1}&m_{2,1}\\m_{1,2}&m_{2,2}\end{matrix}}\right]\left[{\begin{matrix}v_{1}\\v_{2}\end{matrix}}\right]\right)^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/156e9f293c004eb4bf4cf8c0bef876a0c6584e4c)

![{\displaystyle \mathrm {M} =\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bef39ab9b9685594c4aaf79474095159ab373414)

![{\displaystyle \mathrm {M} \;P=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f1a2090b44562c041b9f7f5549082e1a5e80ed3)

















![{\displaystyle \mathrm {M} =\left[{\begin{matrix}\mathrm {A} &\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96250dd40177cef0ba729c12c286bbdaf7180767)

![{\displaystyle \mathrm {M} ^{-1}=\left[{\begin{matrix}\mathrm {A} ^{-1}&-\mathrm {A} ^{-1}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8d5da393e4681b4901251cb4490d91c3e7f752e)
![{\displaystyle \left[{\begin{matrix}\mathrm {A} ^{T}&-\mathrm {A} ^{T}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad350cacc4e5b36c6f47a97249f68bf9d685d09e)


![{\displaystyle \mathrm {M} ^{-1}P=\left[{\begin{matrix}\mathrm {A} ^{T}&-\mathrm {A} ^{T}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]\left[{\begin{matrix}\mathbf {p} \\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17007a999a3d92ddc4df141330c84cab9e786d50)
![{\displaystyle =\left[{\begin{matrix}\mathrm {A} ^{T}\mathbf {p} -\mathrm {A} ^{T}\mathbf {t} \\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae33957e28b8efbfd8c121803067d4b9b70e9455)
![{\displaystyle =\left[{\begin{matrix}\mathrm {A} ^{T}(\mathbf {p} -\mathbf {t} )\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/463820aa06871368c7aeddccf00e8826965bf308)


























