Trigonometry/Sine Squared plus Cosine Squared
Pythagoras in Disguise
[edit | edit source]This formula is the Pythagorean theorem in disguise.
If you look at the diagram in the next section it should be clear why. Sine and Cosine of an angle in a triangle with unit hypotenuse are just the lengths of the two shorter sides. So squaring them and adding gives the hypotenuse squared, which is one squared, which is one.
Pythagorean Trigonometric Identity
[edit | edit source]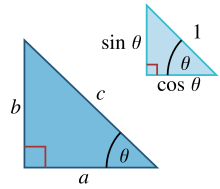
In more detail... In a right triangle with sides and hypotenuse , trigonometry (Soh-Cah-Toa) determines the sine and cosine of the angle between side and the hypotenuse as:
From that it follows:
where the last step applies Pythagoras' theorem. This relation between sine and cosine sometimes is called the fundamental Pythagorean trigonometric identity.[1] In similar triangles, the ratios of the sides are the same regardless of the size of the triangles, and depend upon the angles. Consequently, in the figure, the triangle with hypotenuse of unit size has opposite side of size and adjacent side of size in units of the hypotenuse.
Neither sine nor cosine can ever exceed 1 and the closer one of them is to 1, the closer the other must be to 0. We can see this in two ways:
- It follows immediately from the formula. As either sine squared or cosine squared gets closer to one the amount left for the other diminishes.
- It can be seen from the geometry. The hypotenuse is one and is longer than either of the other sides. As one side gets closer to one, the other must get closer to 0.
Using the Formula
[edit | edit source]|
If , what is ? By the Pythagorean Identity, If , then Solving for , add to both sides to obtain |
This formula and Circles
[edit | edit source]In an earlier exercise we asked you to plot points , and you got a circle - well, you should have done.
For each point you plot, there is a right triangle with coordinates .
The hypotenuse of this triangle is the line from to . The square of the hypotenuse has length and because this is 1, the hypotenuse has length 1. So every point you plotted is at distance 1 from the point which is what is needed for the points all lie on a circle of radius 1, with centre .
You were in fact plotting points which all satisfied . That's because and . If instead you plotted points which satisfied you would get a circle with radius .
Revision
[edit | edit source]|
Revision: Which of the following is/are correct?
|
References
[edit | edit source]- ↑ Lawrence S. Leff (2005). PreCalculus the Easy Way (7th ed.). Barron's Educational Series. p. 296. ISBN 0764128922.



























