Topology/History
It could be said that mathematics in general owes its credibility to ancient Greece's Euclid. What is probably his most famous work, Elements, revolutionized the concepts of geometry and mathematics as a whole through the presentation of a simple logical method. This method is summarized by Leonard Mlodinow:
First, make terms explicit by forming precise definitions and so ensure mutual understanding of all words and symbols. Next, make concepts explicit by stating specific axioms or postulates so that no unstated understandings or assumptions may be used. Finally, derive the logical consequences of the system employing only accepted rules of logic, applied to the axioms and to previously proved theorems [1].
Throughout its history, many mathematicians have influenced the development of topology. While Johann Benedict Listing is not credited with a memorable discovery in terms of the field of topology, he is still considered one of the founding fathers. This is because he gave topology its name. While he published very little on topology, he is remembered for Vorstudien zur Topologie, which was the first document to use the word topologie (English: topology) to describe the field. He is also often credited with discovering the Möbius strip independently of August Ferdinand Möbius [2].
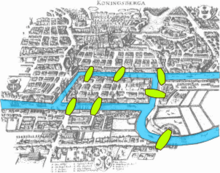
The origins of topology date back to the eighteenth century and the Königsberg Bridge Problem, a problem of relative position without regard to distance [3]. While this problem is often regarded as the birth of graph theory, it also inspired Euler's development of the topology of networks [4]. Königsberg, now Kaliningrad, was founded in 1255 and became a prosperous seaport [5]. The city resides on the banks of the Praegel, now Pregolya, River. Citizens could use seven bridges that crossed the Praegal, but the question of whether or not one could pass through the town and use each bridge exactly once would turn out to be the catalyst in the creation of the mathematical field of topology. Swiss mathematician Leonhard Euler would be the one to discover the answer was no. He determined that the graph defined by the location of the bridge was not what is now called a Eulerian graph [6]. This solution entitled The Solution of a Problem Related to the Geometry of Position was submitted to the Academy of Sciences in St. Petersburg in 1735 [7].

Euler is also well known for his research in the combinatorial qualities of polyhedra. He considered the edges (), which he called acies, the faces (), or hedra, and the vertices (), called angulus solidus. Euler realized the importance of these three properties claiming that they "completely determine the solid". His research resulted in the well-known Polyhedral Formula: . However, Euler's formula applies only to convex solids [8]. In 1813 Antoine-Jean L'Huilier recognized this limitation of the formula and provided a generalization for a solid with holes: . This was the first known result of a topological invariant [9].
August Ferdinand Möbius was one of the main contributors of the topological theory of manifolds. In 1865, Möbius presented an article in which he decomposed several orientations of surfaces in polygonal nets. His most famous example was a non-orientable surface, which is now called the Möbius strip[10].
The Russian born mathematician Georg Ferdinand Ludwig Philipp Cantor, the father of set theory, is another mathematician to whom we owe credit for topology. Concepts of set theory and cardinality are fundamental for the study of topology. Today, Cantor is a truly celebrated mathematician, especially considering that set theory and the idea of infinity do not seem to have a truss of mathematical ideas from which they could have been developed. Sadly, these ideas were not welcomed by a nineteenth century world, and Cantor spent many years of his adult life struggling with public criticism. A German mathematician by the name of David Hilbert described Cantor's discoveries in the infinite domain as an "astonishing product of mathematical thought" [11]. In 1877, Cantor showed that the points on a 2-dimensional square had a one-to-one correspondence with the points on different line segments, and this caused others to begin asking questions about the idea of dimension, leading to the development of dimension theory [12].
In the late 1800s and early 1900s, many mathematicians challenged themselves with more abstract problems. Maurice René Fréchet, a French mathematician, helped these mathematicians considerably in 1906. He explained that if a distance can be defined between two different mathematical entities, then real and complex number concepts can be applied [13]. Fréchet, along with Schoenflies, Hausdorff, and others, would be one of the first to study "general topology" [14]. Fréchet developed the theory of metric spaces, which was based on Cantor's theory of sets [15].
German mathematician Felix Hausdorff followed in Cantor's footsteps with regard to set theory. In fact, Hausdorff was one of the first to teach set theory. In the summer 1901, he had 3 students [16]. The idea that a topology possesses a lattice of open subsets had been around almost as long as the idea of topology itself, but Hausdorff was the first to emphasize the importance of these sets in defining topological concepts [17].
French mathematician and physicist Henri Poincaré discovered his talent at an early age. In fact, he took first place in a national mathematics competition while he was still in school. Poincaré was the first to study Fuchsian groups, dealing mainly with their underlying geometry and topology [18]. Poincaré is most famous for The Poincaré Conjecture which states the following:
A compact smooth n-dimensional manifold that is homotopy equivalent to the n-sphere must in fact be homeomorphic to . One can think of a compact manifold as a manifold that lives in a finite region of for some and that has no boundary [19].
This conjecture would not be proven until 2003 by Grigory Perelman [20].
References
[edit | edit source]- ↑ Mlodinow, Leonard. Euclid's Window: The Story of Geometry from Parallel Lines to Hyperspace. New York: Simon & Schuster, Inc. 2001
- ↑ Breitenberger, E. Johann Benedikt Listing. History of Topology. James, Ioan Mackenzie. Amsterdam: Elsevier BV, 1999. 909-924
- ↑ Königsberg bridge problem. Encyclopædia Britannica Online. 2011. http://www.britannica.com/EBchecked/topic/321794/Konigsberg-bridge-problem
- ↑ Goodwin College of Professional Studies. ``The Beginnings of Topology". Drexel University. 1998. http://mathforum.org/isaac/problems/bridges1.html
- ↑ ``Königsberg". Encyclopedia Americana. 1831. Vol. 7 Pg. 345
- ↑ Singh, Suresh, G. Graph Theory. New Delhi: PHI Learning Private Limited, 2010
- ↑ Wilson, Robin J. "Graph Theory". History of Topology. James, Ioan Mackenzie. Amsterdam: Elsevier BV, 1999. 503-530
- ↑ Richeson, David. "The Polyhedral Formula". Leonhard Euler: Life, Work, and Legacy. Bradley, Robert E., Sandifer, Charles Edward. Amsterdam: Elsevier BV, 2007
- ↑ O'Connor, J. and Robertson, E. "A History of Topology". University of St. Andrews. 1996. http://www-history.mcs.st-andrews.ac.uk/HistTopics/Topology\_in\_mathematics.htm
- ↑ Pickover, Clifford A. The Möbius Strip: Dr. August Möbius's Mathematical Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. Thunder's Mouth Press, 2007
- ↑ Crilly, T. and Johnson, D. "The Emergence of Topological Dimension Theory". History of Topology. James, Ioan Mackenzie. Amsterdam: Elsevier BV, 1999. 1-24
- ↑ Krantz, Steven G. An Episodic History of Mathematics: Mathematical Culture Through Problem Solving. The Mathematical Association of America, 2010
- ↑ Rezende, Lisa. Chronology of Science. New York: Infobase, 2006
- ↑ Eynde, R. Vanden. "Development of the Concept of Homotopy". History of Topology. New York: Elsevier BV, 1999. 65-102
- ↑ Truesdell, Clifford. Archive for History of Exact Sciences. Springer-Verlag, 1998
- ↑ Hausdorff, Felix, Plotkin, Jacob M. Hausdorff on Ordered Sets. American Mathematical Society, 2005
- ↑ Aull, Charles E., Lowen, Robert. Handbook of the History of General Topology. Dordrecht: Kluwer Academic Publishers, 2001
- ↑ Stillwell, John. Mathematics and its History. San Francisco: Springer-Verlag, 2002
- ↑ Gowers, Timothy, Barrow-Green, June, Leader, Imre. The Princeton Companion to Mathematics. Princeton: Princeton University Press, 2008
- ↑ O'Shea, Donal. The Poincare Conjecture: In Search of the Shape of the Universe. New York: Walker Publishing Company, Inc., 2010








