TI 83 Plus Assembly/Printable version
| This is the print version of TI 83 Plus Assembly You won't see this message or any elements not part of the book's content when you print or preview this page. |
The current, editable version of this book is available in Wikibooks, the open-content textbooks collection, at
https://en.wikibooks.org/wiki/TI_83_Plus_Assembly
What you need
You need a few basic things to begin programming.
- A calculator. A TI 83 Plus, TI 83 Plus Silver Edition, TI 84 Plus or TI 84 Plus Silver Edition is needed.
- An assembler. Such programs "assemble" the assembly code you will write into a form that the calculator can execute. Some assemblers include:
- TASM. Tasm did not work with enclosed examples. Downloading executable files via the internet is always risky. Does not work for Turbo Assembler 5 code.
- Brass is an assembler targeted at the TI-83+, written by Benjamin Ryves. It is no longer maintained.
- Zilog Developer Studio is Zilog's official IDE. Various versions can be found on Zilog's website.
- Spasm-ng is a z80/ez80 assembler that includes features targeted towards TI calculators. Builds for various systems are available on the download page.
- TI 83 Plus Include File. This text file assists the assembler by giving it necessary information when assembling. Does not recognize instructions.
- DevPac8x. This program changes the code that TASM has assembled into a file that you can transfer to your calculator.
- TI SDK (Software Development Kit). Also known as the TI 83 Plus Flash Debugger, this program allows programs to be tested on the computer for errors without having to transfer them to the calculator.
- Linking cable. A linking cable will allow you to transfer your programs to the calculator from the computer.
Now that you have everything, you will need to set everything up. I highly recommended that you follow the examples I give.
- Make a folder where you will put all your ASM (assembly) files (e.g. C:\ASM).
- Unzip the TASM folder into a subfolder in your ASM folder titled "TASM" (e.g. C:\ASM\TASM).
- Put the ti83plus.inc file into your TASM folder.
- Unzip the DevPac8x folder into a subfolder titled "devpac8x" (e.g. C:\ASM\devpac8x).
- Make another subfolder titled "Programs" (e.g. C:\ASM\Programs). This folder will be where you put all your programs in.
- Install the TI SDK.
- You need to open Notepad and type the following text in:
@echo off echo Compiling... move %1.z80 ..\tasm cd ..\tasm tasm -t80 -i -b %1.z80 %1.bin move %1.z80 ..\programs move %1.bin ..\devpac8x cd ..\devpac8x devpac8x %1 move %1.bin ..\programs move %1.8xp ..\programs cd ..\programs echo Done!
Save this as "compile.bat" into your Programs folder. And finally you need to make sure you know how to operate the link and turn on your calculator...
That is all you need to get started!
Also see Alternate Methods. The above instructions do not work on an x64 bit architecture.
Hello World
In this section you will make a program to display "Hello, World" on the screen.
Writing the Program
[edit | edit source]Make a new text file on NotePad and type the following text:
.NOLIST
#define EQU .equ
#define equ .equ
#define END .end
#define end .end
#include "ti83plus.inc"
.LIST
.org 9D93h
.db $BB,$6D
ld a,0 ; load the value 0 to register a, the ''accumulator''
ld (CURCOL),a ; assign the contents of register a to memory address (CURCOL) in the RAM
ld (CURROW),a ; assign the contents of register a to memory address (CURROW) in the RAM
ld hl,text ; load the data in label "text" to register hl
B_CALL(_PutS) ; calls a function in ti83plus.inc to print text
B_CALL(_NewLine) ; calls a function in ti83plus.inc to insert a lnbreak (for legibility)
ret ; returns from the program to the calc's OS
text:
.db "Hello, World",0
.end
end
The tabbed lines need to be tabbed! Save this file as myprog.z80 into your "Programs" subfolder. Also, note that the command B_CALL() may need to be changed to bcall() depending on the contents of the includes file used during compiling. The compiler will record one error if the command (B_CALL or bcall) is different than the one defined in ti83plus.inc, though in the most popular editions of ti83plus.inc it is bcall - simply swapping one for the other may fix this.
Compiling the Program
[edit | edit source]Compiling essentially means translating text code into code that a machine can read.
To compile your program myprog.z80 first open a Command Prompt (it should be in Accessories). You should be faced with a black window with some white text saying what folder you are in. The first step is to change the folder to your programs folder. To do this use the following commands:
- cd subfoldername (This will go to the subfolder that you tell it to.)
- cd .. (This will instantly go to the folder that holds the folder you are in.)
Afterwards, you need to type in:
- compile myprog
This should automatically compile myprog.z80 if you have followed all instructions correctly.
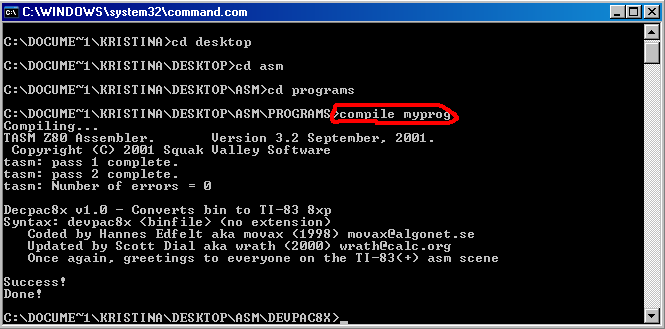
The finished program should be located in your "Programs" folder as myprog.8xp.
Testing the Program
[edit | edit source]On your computer, open up the TI 83 Plus Flash Debugger to make a fake calculator for testing purposes. Click on the white paper icon to make a new fake calculator and choose the 83+ calculator. Then click on Load... RAM File and open your compiled program (myprog.8xp). Finally, click on the triangle-shaped play button to begin emulation. On the fake calculator, press [2nd]+[Catalog] to bring up the catalog and arrow down to Asm(. Press enter to insert the command into the screen and then select your program ([PRGM],[ENTER]). The screen on the calc should say Asm(prgmMYPROG). Now press enter, and "Hello World" should be displayed on the screen.
Always test your programs on the Flash Debugger before you use them on your real calculator because there is a large chance of your real calculator crashing.
Commands of the Program
[edit | edit source]The only lines of importance now are the middle ones:
ld a,0
ld (CURCOL),a
ld (CURROW),a
ld hl,text
B_CALL(_PutS)
ret
text:
.db "Hello, World",0
When the calculator executes a program, it follows the commands line by line. The first line (ld a,0) loads zero into a, which is a commonly used register. So now register a = 0. The next two lines load that number into the cursor row and column sectors in the RAM. So now the cursor is located at 0,0 and the next text will be displayed at that location. The fourth line (ld hl,text), loads the location of .db "Hello... into hl, another register. B_Call(_PutS) takes the text that hl has specified and displays it at the current cursor location. Finally, ret tells the calculator to exit out of the program. You should now have a vague understanding of the functions of most of the lines in your first program.
This little program, however small, is far from optimal. ld a,0 can be replaced by xor a as long as you don't need to preserve the flags. XOR A (see [1]) inverts any bit that is 1, so basically it sets A to zero. This is not all, one can load CurCol and CurRow at once with ld (CurRow),hl , L will go into CurRow and H into CurCol.
ld hl,0
ld (CurRow),hl
ld hl,text
B_CALL(_PutS)
ret
text: .db "Hello, World",0
Jumps
jp
[edit | edit source]In the previous program a label was written:
text:
.db "Hello, World",0
text: is a label. Labels are never tabbed and always end with a colon. Labels are actually 16-bit numbers, pointing to the instruction directly following them. Thus labels are actually 16-bit immediate numbers and can be treated the same (the same loads apply to them). They mark a place in a program. You can jump to a label by using jp labelname:
.NOLIST
#define END .end
#define end .end
#define equ .equ
#include "ti83plus.inc"
.LIST
.org 9D93h
.db $BB,$6D
jp clearscreen ;here it is
ld a,0
ld (CURCOL),a
ld (CURROW),a
ld hl,text
B_CALL(_PutS)
ret
text:
.db "Text",0
clearscreen: ;and here it goes
B_CALL(_ClrLCDFull)
.end
end
(B_CALL(_ClrLCDFull) clears the screen.) The program above clears the screen but never displays text. Why? Because jp clearscreen automatically jumps to the label clearscreen and contintues until the end of the program, skipping over all the text display code.
jp label is equal to this invalid-syntax code LD PC,label.
By the way, the stuff followed by the semicolon are comments: they are used to explain the code and are ignored by the compiler. (The compiler is the program which converts the code you write to code a machine can read.)
jr
[edit | edit source]jr is a jumping instruction similar to jp, but with a few important differences. It's one byte smaller (this may not seem like a lot, but it can add up); however, unlike jp (which can jump to any address), jr can only jump to a label that's up to 127 bytes forward or up to 128 bytes backward in your code. So, use jp if the label is far away but otherwise use jr. In fact, you may want to always use jr, because when you compile an error will be returned if the label is too distant. The compiler subtracts the address to which the label behind the jr is pointing to from the address of the label itself, if the result does not fit in a signed 8-bit number it will throw an error because it can not be compiled (address exceeds range). JR's are always slower than JP's, and you can not use all conditions with them. JR can use the conditions Z, NZ, C and NC, whereas JP, RET and CALL can use the conditions Z, NZ, C, NC, PO (parity odd), PE (parity even), P (positive)and M (negative).
The jump in the above program could be replaced with jr:
.NOLIST
#define END .end
#define end .end
#define equ .equ
#include "ti83plus.inc"
.LIST
.org 9D93h
.db $BB,$6D
jr clearscreen ;this saves space!
call
[edit | edit source]Imagine if you want to jump somewhere and then go back. CALL pushes its address +3 on the stack; RET pops the top of the stack in PC. This is the very same stack as the PUSH-POP stack, so be careful. Use call and ret to 'jump' somewhere and return:
.NOLIST
#define END .end
#define end .end
#define equ .equ
#include "ti83plus.inc"
.LIST
.org 9D93h
.db $BB,$6D
call clearscreen ;1. here it is
ld a,0 ;4. to here
ld (CURCOL),a
ld a,0
ld (CURROW),a
ld hl,text
B_CALL(_PutS)
ret ;5. and ends
text:
.db "Text",0
clearscreen: ;2. here it goes
B_CALL(_ClrLCDFull)
ret ;3. then it comes back
.end
end
As you can see, the first ret (right after the _ClrLCDFull) went back to after the call command. Then, the second ret ended the program. You can think of your program as one big call routine, with the ending ret going back to the main calculator. Warning: Calls interfere with stacks.
These jumps can be combined with code learned in later sections.
Registers
Many parts of this page are based highly upon taken from Sean McLaughlin's Learn Assembly in 28 Days, Day 3.
Number Systems
[edit | edit source]Necessary reading, this. Computers don't count the same way you and I do.
Decimal
[edit | edit source]All number systems use a particular radix. Radix is synonymous with "base" if it helps, although I should caution you that saying such things as "All you radix are belong to us" is a great way to get people to throw pointy things at you (but whether it's because of the horrid pun or the tired pop-culture reference is hard to say... :-). To understand what a radix is, consider our everyday system of numbers, which uses base ten.
Like you learned in grade school and forgot over summer, in a base ten number, each digit specifies a certain power of 10, and as a consequence you need ten different digits to denote any number. The rightmost digit specifies 100, the second digit specifies 101, the third 102 and so on. You can, therefore, break down a decimal number, such as 276310, like this (although it does wind up to be redundant):
276310 = (2 x 103) + (7 x 102) + (6 x 101) + (3 x 100)
= (2 x 1000) + (7 x 100) + (6 x 10) + (3 x 1)
= 2000 + 700 + 60 + 3
= 276310
Computers enjoy working with two other bases: binary and hexadecimal. Octal is base-8, and seems to have died out. The only operating system to use octal was UNIX.
Binary
[edit | edit source]Binary is a base-2 system, so it uses only two digits (0 and 1), and each digit represents a power of 2:
101101012 = (1 x 27) + (0 x 26) + (1 x 25) + (1 x 24) + (0 x 23) + (1 x 22) + (0 x 21) + (1 x 20)
= (1 x 128) + (0 x 64) + (1 x 32) + (1 x 16) + (0 x 8) + (1 x 4) + (0 x 2) + (1 x 1)
= 128 + 32 + 16 + 4 + 1
= 18110
A single binary digit is familiarly called a bit. Eight bits are called a byte. Other combinations you could hear about: Name Size nibble 4 bits word 16 bits dword 32 bits quadword 64 bits Since the Z80 can directly manipulate only bytes and words (and nibbles in some circumstances), the majority of data handling you do will involve mostly those, so you don't have to concern yourself with the others too much (although it would still be a good idea to familiarize yourself with them).
We will find ourselves working with, or at the very least referencing the individual bits of a byte or word. The nomenclature:
- If we arranged the bits out horizontally, we call the rightmost bit "bit 0", and each bit to the left is given a number one greater.
- The leftmost and rightmost bits are given special names: the leftmost bit is called the high-order bit or the most-significant bit (since it controls the highest power of two of the number, it makes the most significant contribution to the value). The rightmost bit is called the low-order bit or the least-significant bit.
- We can apply these points to nibbles in a byte, bytes in a word or dword, etc. So for example the rightmost byte in a 64-bit quantity would be termed the least-significant byte.
Hexadecimal
[edit | edit source]Hexadecimal is base-16, so it uses 16 digits: the regular digits 0 to 9, and the letters A to F that correspond to the decimal values 10 to 15.
1A2F16 = (1 x 163) + (10 x 162) + (2 x 161) + (15 x 160)
= (1 x 4096) + (10 x 256) + (2 x 16) + (15 x 1)
= 4096 + 2560 + 32 + 15
= 670310
Hex values have an interesting relationship with binary: take the number 110100112. In hex, this value is represented as D316, but consider the individual digits:
D16 = 11012
316 = 00112
Compare these two binary numbers with the original. You should see that one hex digit is equivalent to one nibble. This is what's so great about hexadecimal, converting binary numbers used by the computer into more manageable hex values is a snap.
Designating Base
[edit | edit source]To designate base above, we have adopted the notation used by many mathematicians by writing the radix as a subscript. Too bad we must write assembly code in plain text format, which has no capability for such niceties. The way to denote radix varies, but in all cases it involves attaching an extra character or characters to the number. TASM gives you a choice between a symbolic prefix or an alphabetic suffix.
Prefix Format Suffix Format Base %10011011 10011011b Binary $31D0 31D0h Hexadecimal @174 174o Octal 12305 * 12305d Decimal * no prefix
It doesn't matter which format you use, provided you don't mix them (like $4F33h). The prefix formats may be easier to read, since the letter sort of gets lost among the numbers (especially if it's upper case).
Registers
[edit | edit source]Registers are sections of very expensive RAM inside the CPU that are used to store numbers and rapidly operate on them. There are fourteen registers on this CPU: A B C D E F H I L R PC SP IX and IY. You don't need to concern yourself about registers I, R, PC and SP yet.
The single-letter registers are 8 bits in size, so they can store any number from 0 to 255. Since this is oftentimes inadequate, they can be combined into four register pairs: AF BC DE HL. These, along with IX and IY, are 16-bit, and can store a number in the range 0 to 65535.
These registers are general purpose, to a point. What I mean by that is that you can usually use whichever register you want, but many times you are forced to, or it's just better to, use a specific one. For example, only the HL, IX and IY registers can be used for indirect memory addressing when loading into registers other than A, all 16-bit registers can be used to load to or from an indirectly addressed memory location when loading from or to (respectively) register A.
The special uses of the registers:
8-bit Registers:
- A is also called the "accumulator". It is the primary register for arithmetic operations and accessing memory. Indeed, it's the only 8-bit register you can use.
- B is commonly used as an 8-bit counter.
- C is used when you want to interface with hardware ports.
- F is known as the flags. The bits of this register signify (that is to say they "flag") whether certain events have occurred. For example, one of the flags (bits) reports if the accumulator is zero or not. The uses of the flags will be explained at a later day because we have no use for them at this point.
- I is the high byte of the interrupt vector when the processor is in Interrupt Mode 2 (IM 2), the low byte of the vector comes from the data bus and is functionally random. Note that this vector is used to load a value from RAM first, then that address is called. You can only load to and from it using A.
- R is the dynamic RAM refresh register, it increases after every instruction by an amount depending on the instruction. Its contents are pseudo random. You can only load to and from it using A.
The two bytes of all 16-bit registers can be used separately as well.
16-bit Registers:
- AF is only used in pushes and pops.
- HL has two purposes. One, it is like the 16-bit equivalent of the accumulator, i.e. it is used for 16-bit arithmetic. Two, it stores the high and low bytes of a memory address.
- BC is used by instructions and code sections that operate on streams of bytes as a byte counter.
- DE holds the address of a memory location that is a destination.
- PC holds the address of the currently executing instruction, you can only change its contents with jumps, calls and rets. The only way to load directly to it is 'jp (hl)' you could see this as a 'ld pc,hl'.
- SP is the Stack Pointer, it determines where in RAM values are Pushed and Popped, you can only load to it using HL, and you can only load from it using arithmetic like 'add hl,sp', if HL was zero before the addition it now holds the value of SP.
- IX and IY is a funky li'l registers called the index registers. Almost everywhere HL is acceptable, so too is IX and IY. Important to note that using IX and IY results in slower and more inflated code than HL would (approximately double the size and time) because they were not present on the 8080 (the processor the Z80 is based on), so use it only when necessary (usually when HL is tied up). IX and IY can do something special that no other register can though, we'll look at that in due time.
To store to a register, you use the LD instruction.
LD destination, source Stores the value of source into destination.
There are many more, but they involve registers you haven't heard of yet.
Note: imm8: 8-bit immediate value. imm16: 16-bit immediate value.
Destination source A B C D E H L BC DE HL (BC) (DE) (HL) (imm16) A * * * * * * * * * * * B * * * * * * * * C * * * * * * * * D * * * * * * * * E * * * * * * * * H * * * * * * * * L * * * * * * * * BC * DE * HL * (BC) * (DE) * (HL) * * * * * * * (imm16) * * * * imm8 * * * * * * * * imm16 * * *
You obviously have no clue what difference parentheses make for an operand. You'll see shortly. You can only to/from I and R using A.
Examples:
LD A, 25 Stores 25 into register A LD D, B Stores the value of register B into register D. LD ($8325), A Stores the value of register A into address $8325 (explained later on).
Some points that should be made clear:
The two operands for LD cannot both be register pairs, excepting SP. You have to load the registers separately:
; Since we can't do LD DE, HL... LD D, H LD E, L ; But we can do this: LD SP,HL ; The following instruction effectively loads HL into PC JP (HL)
If you use LD with a number that is too big for the register to hold, you will get an error at assembly time. Storing negative numbers, however, is legal, but the number will get "wrapped" to fit. For example, if you assign -1 to A, it will really hold 255. If you assign -2330 to BC, it will really hold 63206. Adding one plus the maximum value the register will hold gives you the value that will be stored. There is a reason for this phenomenon that will be made clear shortly.
An instruction similar to LD but functionally different, is EX. Despite the fact that it is very particular about its operands, it is a very useful instruction. (90% of the time the registers you want to exchange are HL and DE).
EX DE, HL Swaps the value of DE with the value of HL.
If you want to swap and other register pair with HL (or an index register) without losing an other register you could do the following (although slow)
PUSH BC EX (SP),HL POP BC
Registers F and AF cannot be used as operands for the LD instruction. Actually, these registers can not be operands for any instruction barring a few.
Negative Numbers
[edit | edit source]Up to this point there has been an implication that registers are only capable of assuming positive values, but in the real world negative numbers are just as common. Fortunately, there are ways to represent negative numbers. In assembly, we can attribute a number as either signed or unsigned. Unsigned means that the number can only take on positive values, signed means that the number can be either positive or negative. It is this concept of signed numbers we need to look at.
It turns out that there are many signed numbering schemes, but the only one we're interested in is called two's complement. When we have a signed value in two's complement, the most significant bit of the number is termed the sign bit and its state determines the sign of the number. The existence of the sign bit naturally imposes a restriction on the number of bits a number may be composed of. With this, the amount of bits at our disposal to represent the number is reduced by one; for a string of eight bits, we can have a numeric range of -128 to +127 in decimal. For a string of sixteen, it's -32768 to 32767, etc.
As to what bearing the state of the sign bit has on the value, it is this: if the sign bit is clear, the value is a positive quantity and is stored normally, as if it were an unsigned number. If the sign bit is set, the value is negative and is stored in two's complement format. To convert a postive number to its negative counterpart, you have two methods, either of which you can choose based on convenience.
- Calculate zero minus the number (like negative numbers in the Real World). If you're confused how to do this, you can consider 0 and 256 (or 65536 if appropriate) to be the same number. Therefore, -6 would be 256 - 6 or 250: %11111010.
- Flip the state of every bit, and add one. Therefore, -6 would be %11111001 + 1 or %11111010.
There is one special case of two's complement where negation fails, and that is when you try to negate the smallest negative value:
%10000000 -128
%01111111 Invert all bits
%10000000 Add one (=-128)
Of course -(-128) isn't -128, but the value +128 cannot be represented in two's complement with just eight bits, so the smallest negative value can never be negated.
There is an instruction to automate two's complement: NEG Calculates the two's complement of the accumulator. I'm sure you find the theory wonderfully engrossing, but what you're probably interested in is how the CPU handles the difference between unsigned and signed numbers. The answer is, it doesn't. You see, the beauty of two's complement is that if we add or subtract two numbers, the result will be valid for both signed and unsigned values:
unsigned signed
%00110010 5 5
+ %11001110 + 206 + -5
%1 00000000 256 0 (Disqualify ninth bit)
This phenomenon was not lost on the makers of the Z80. You could use the same hardware for adding signed numbers as unsigned numbers only with two's complement, and less hardware means a cheaper chip (true, nowadays you can get a fistful of Z80s for fifty cents, but back in 1975 it was a big deal, just look at the 6502).
Memory
Main memory map
[edit | edit source]The basic memory map of the TI-83+ looks like this:
- $0000–$3FFF: Boot ROM page (fixed)
- $4000–$7FFF: Swappable Memory block A
- $8000–$BFFF: Swappable Memory block B
- $C000-$FFFF: Swappable RAM block
You generally won't care about what's in $0000–$7FFF, and I wouldn't try changing anything in that range. Unless you're writing a Flash app, which executes in $4000-$7FFF. $8000–$FFFF is the calculator's RAM and contains fixed locations, fixed variables, and Flags used by the OS. IY should always point to these flags so do not mess with IY unless you know what you're doing. Know however that PUSH and POP change the memory at $C000-$FFFF, and that you can NOT execute in this area.
Data Types
Data types on the TI 83+/84+
[edit | edit source]There are only 5 data types for the TI 83+/84+, one of them being an emulated one (not supported by hardware, calculated in software).
The data types are:
- uByte 8-bit value in the range of 0 through 255
- sByte 8-bit signed value in the range of -128 through 127
- Word 16-bit value in the range of 0 through 65535
- sWord 16-bit signed value in the range of -32768 through 32767
- TI float, 9 bytes, 1 sign byte, 1 signed exponent, 7 BCD bytes of the mantissa.
sword is a signed word, not a piece of metal, TI floats are not supported by hardware.
Assemblers often use db for a byte (signed or unsigned) and dw for a word (signed or unsigned).
Although TI floats are not supported by hardware, there are a lot of ROM calls for them, most of which can be found in '83psysroutines.pdf' which can be downloaded from TI's site.
For math with other data types it is best to take a look at z80bits (archived page)
Input
Input
[edit | edit source]There are three ways to receive input from an assembly program on your TI-83+. The first two are ROM calls, and the last one is directly interfacing with the calculator's keypad.
The ROM calls
[edit | edit source]These are two routines called with the b_call() macro. They are both good ways to receive input.
GetKey
[edit | edit source]This routine will wait for the user to press a key, and only when the user does, will it return to the main program. What is nice about this routine is that it processes [2nd] and [Alpha] key presses for you. Parameters: None Returns:Key value in the accumulator To see a list of the codes, click here
Example:
.include "ti83plus.inc" . . . waitForUser: bCall(_GetKey) ; [x]Or: rst $28 \ .dw $4972 ; [x]Or: bCall($4972) cp kEnter jr nz,waitForUser jr continue continue: . . .
So, the example is a simple program that pauses execution until the user presses the [Enter] key.
GetCSC
[edit | edit source]This routine is like the GetKey routine, except for two things. The first is that, unlike the GetKey routine, it will not wait for the user to press a key. The second is that it uses a different set of key codes, which you can find here. Also, it does not process key combinations, but you can make your own parser for them.
Parameters: None Returns:Key Code in accumulator if key was pressed, else 0 (In the accumulator). Example:
.include "ti83plus.inc" . . . waitForUserCSC: bCall(_GetCSC) cp 0 jr z,waitForUserCSC jr nz,continue continue: . . .
This example waits until ANY key is pressed.
Direct Input
[edit | edit source]Note:This is a more advanced method, because it deals directly with the keyboard driver. The keypad of the TI 83+ calculator is divided into Seven sections. These are:
- The arrow keys
- [ENTER], going vertically to [CLEAR]
- [(-)], going vertically to [VARS]
- [.], going vertically to [DEL]
- [0], going vertically to [MODE]
- [STO->], going vertically to [2ND]
- [Y=], going horizontally to [GRAPH]
To read a value from the keys of a group, you must first turn the group on. This is done by writing to port 1 (01 hex.).
Bit 0 - Group 1
Bit 1 - Group 2
Bit 2 - Group 3
And so on. To turn a group on, you set its designated bit to 0 (zero).
Example:
. . .
waitForUserInputDirect:
; You cannot write an actual value to one of the ports. You must forward it through the (a) register.
; Use group '1'
ld a,%11111101
out ($01),a
; Read in a value
in a,($01)
; Test bit 0 (Enter)
bit 0,a
; If true, goto continue
jr z,continue
; Else
jr waitForUserInputDirect
continue:
. . .
It does the same thing as the previous two examples. Note that this method does not require any ROM calls, and is less readable. For a list of keycodes, go here.
Advanced
Advanced z80 programming techniques
[edit | edit source]Hooks
[edit | edit source]Interrupts
[edit | edit source]What are interrupts?
[edit | edit source]Types of interrupts
[edit | edit source]Type 0
[edit | edit source]Type 1
[edit | edit source]Type 2
[edit | edit source]How to code them
[edit | edit source]How to install them
[edit | edit source]Principles
[edit | edit source]The jump table
[edit | edit source]Direct LCD Interaction
[edit | edit source]Principles
[edit | edit source]Port $10
[edit | edit source]Writing
[edit | edit source]Reading
[edit | edit source]Port $11
[edit | edit source]Writing
[edit | edit source]Reading
[edit | edit source]Optimizations
[edit | edit source]xor a
[edit | edit source]A common shortcut to set the accumulator (A) to zero is by xor'ing it against itself:
; instead of doing this
ld a,0
; you can do this
xor a
This is incredibly widespread and won't affect the readability of your code. In fact, it is so common that it might even be more readable than using "ld a,0". But be warned that "xor a" modifies the flags (it sets the z flag and resets the carry, for example) whereas "ld a,0" doesn't modify any flags.
ld (addr),reg16
[edit | edit source]When writing to two consecutive bytes in memory, it can often be faster and smaller to use a 16-bit register rather than two loads with a.
; rather than
ld a,$10
ld (penCol),a
ld a,$20
ld (penCol),a
; you can do
ld de,$2010
ld (penCol),de
This loads e into (penCol), and d into (penCol+1). penCol+1 is penRow. Keep in mind, however, that using hl to read/write from addresses in memory is (4 t-states) faster and one byte smaller than using de/bc.
X <= A <= Y
[edit | edit source]If you want to know if the value of the accumulator is between two other values, eg. 10 and 25, you might be tempted to do something like this:
cp 10 ; check if a >= 10
jr c,wrongValue
cp 26 ; check if a <= 25
jr nc,wrongValue
; do whatever you wanted to do
wrongValue:
; ...
However, rather than doing two comparisons and jumps, you can change the first cp into a subtraction. This turns any number less than 10 into a negative number. For example:
sub 10 ; a value of 10 now equals 0
cp 26-10 ; because of the sub 10, we now need to check if a is between 0 and 16, not 10 and 26
jr nc,wrongValue
; do whatever you wanted to do
wrongValue:
; ...
This method lets you avoid the first jr.
Appendix A
ROM Calls
[edit | edit source]This Appendix shows information about many ROM Calls that can be used when programming in TI 83 Plus Assembly.
Display
[edit | edit source]Bit_VertSplit
[edit | edit source]Tests if the TI−83 Plus is set to G-T (graph-table) display mode.
Output
NZ is set if G-T is set
Example
B_Call(Bit_VertSplit) JR NZ,Screen_is_Split
CheckSplitFlag
[edit | edit source]Checks if either horizontal or G-T split screen modes are active.
Input
grfSplitOverride, (IY + sGrFlags) = 1 to ignore split mode settings
Output
NZ is set if split screen mode is active
Under construction... Please see this pdf [[2]] for Texas Instrument's documentation on all B_Call's.
TI's list is far from complete, consider looking at: [3]
Appendix B
Most System Flags
[edit | edit source]| Flag | Value | IY Offset | Value | Effect |
|---|---|---|---|---|
| TrigDeg | 2 | TrigFlags | 0 | 0 - Radian Mode 1 - Degree Mode |
| DonePrgm | 5 | DoneFlags | 0 | 1 - Display "Done" after program |
| PlotLoc | 1 | PlotFlags | 2 | 0 - Graph and draw routines sent to screen and PlotSScreen 1 - Graph and draw routines sent to screen only. |
| PlotDisp | 2 | 0 - Homescreen is displayed 1 - Graph screen is displayed. |
||
| GrfFuncM | 4 | GrfModeFlags | 2 | 1 - Function graphing mode |
| GrfPolarM | 5 | 1 - Polar graphing mode | ||
| GrfParamM | 6 | 1 - Parametric graphing mode | ||
| GrfRecurM | 7 | 1 - Recursive (Sequence) graphing mode | ||
| GraphDraw | 0 | GraphFlags | 3 | 1 - Graph must be redrawn 0 - Graph is okay. |
| GrfDot | 0 | GrfDBFlags | 4 | 1 - Dot graph mode 0 - Connected graph mode |
| GrfSimul | 1 | 1 - Simultaneous graphing 0 - Sequential graphing |
||
| GrfGrid | 2 | 1 - Grid displayed 0 - No grid |
||
| GrfPolar | 3 | 1 - Polar coordinates 0 - Rectangular coordinates |
||
| GrfNoCoord | 4 | 1 - Don't display coordinates 0 - Display coordinates |
||
| GrfNoAxis | 5 | 1 - Don't display the axis 0 - Display the axis |
||
| GrfLabel | 6 | 1 - Display axis labels 0 - Don't display axis labels |
||
| TextEraseBelow | 1 | TextFlags | 5 | 1 - When displaying a small character, erase the pixels below it. |
| TextScrolled | 2 | 1 - Text display caused screen to scroll | ||
| TextInverse | 3 | 1 - Display text as white-on-black. | ||
| TextInsMode | 4 | 1 - Insert mode 0 - Overstrike mode |
||
| ApdAble | 2 | ApdFlags | 8 | 1 - APD™ is active |
| ApdRunning | 3 | 1 - APD™ clock is running | ||
| OnRunning | 3 | OnFlags | 9 | 1 - Calculator is on. |
| OnInterrupt | 4 | 1 - The [ON] key was pressed | ||
| StatsValid | 6 | StatFlags | 9 | 1 - Statistics results are valid |
| StatANSDisp | 7 | 1 - Display statistics results | ||
| FmtExponent | 0 | FmtFlags | 10 | 1 - Show exponent 0 - No exponent |
| FmtEng | 1 | 1 - Engineering notation 0 - Scientific Notation |
||
| FmtHex | 2 | If FmtHex and FmtOct are 1, then...
|
||
| FmtOct | 3 | |||
| FmtBin | 4 | |||
| FmtReal | 5 | 1 - Real math mode | ||
| FmtRect | 6 | 1 - Rectangular complex mode (a+bi) | ||
| FmtPolar | 7 | 1 - Polar complex mode (re^θi) | ||
| CurAble | 2 | CurFlags | 12 | 1 - Cursor flash is enabled |
| CurOn | 3 | 1 - Cursor is showing | ||
| CurLock | 4 | 1 - Cursor is locked off | ||
| AppTextSave | 1 | AppFlags | 13 | 1 - Written characters are saved in the TextShadow buffer. |
| AppAutoScroll | 2 | 1 - Screen automatically scrolls when the 5x7 font is written and goes beyond the edge of the screen. | ||
| WebMode | 0 | SeqFlags | 15 | 1 - Web mode 0 - Normal sequence mode |
| SeqUV | 2 | 1 - Sequence mode: U vs. V | ||
| SeqVW | 3 | 1 - Sequence mode: V vs. W | ||
| SeqUW | 4 | 1 - Sequence mode: U vs. W | ||
| IndicRun | 0 | IndicFlags | 18 | 1 - Run indicator is on. 0 - Run indicator is off |
| IndicOnly | 2 | 1 - Interrupt handler only checks run indicator (don't process APD™, blink the cursor, or scan for keys). | ||
| Shift2nd | 3 | ShiftFlags | 18 | 1 - [2nd] key was pressed. |
| ShiftAlpha | 4 | 1 - [ALPHA] key was pressed. | ||
| ShiftLwrAlph | 5 | 1 - Lowercase mode set. | ||
| ShiftALock | 6 | 1 - Alpha lock is active | ||
| ShiftKeepAlph | 7 | 1 - Alpha lock cannot be canceled. | ||
| AutoFill | 4 | TblFlags | 19 | 1 - Ask for independent variable in table 0 - Fill table automatically. |
| AutoCalc | 5 | 1 - Ask to calculate dependent variable in table. 0 - Calculate automatically | ||
| ReTable | 6 | 1 - Table has to be recalculated. 0 - Table is okay. | ||
| GrfSplit | 0 | SGrFlags | 20 | 1 - Horizontal split mode |
| VertSplit | 1 | 1 - Vertical split mode | ||
| GrfSplitOverride | 3 | 1 - Ignore graph split flag | ||
| TextWrite | 7 | 1 - Small font writes to PlotSScreen 0 - Small font writes to display. | ||
| LwrCaseActive | 3 | AppLwrCaseFlag | 36 | 1 - Lowercase enabled. Press [ALPHA][ALPHA] to access lowercase characters. |
| FullScrnDraw | 2 | ApiFlg4 | 43 | 1 - Allows graphics commands to use row 0 and column 95 |
| FracDrawLFont | 2 | FontFlags | 50 | 1 - Routines that normally display small font now display large font. |
| CustomFont | 7 | 1 - Small font drawing routines use your own characters. | ||
| BufferOnly | 0 | PlotFlag3 | 60 | 1 - Drawing routines written to PlotSScreen instead of display. |
| UseFastCirc | 4 | 1 - Circles drawn in sections simultaneously. 0 - Circles drawn in a circular direction. | ||
| Asm_Flag1 Asm_Flag2 Asm_Flag3 |
33 34 35 |
Not used by the calculator. Use these for your own personal use. | ||
Appendix C
The following tables show all the key codes that can be accessed with GetKey or GetSCS. These may also be found inside ti83plus.inc.
GetKey Codes
[edit | edit source]
Accessed with B_Call(_GetKey). After the command, the key code is stored into the accumulator and (KeyExtend). Alpha-Alpha Function Keys must be enabled with the following system flag:
SET LwrCaseActive,(IY+AppLwrCaseFlag)
Primary Function Keys
[edit | edit source]| Key | Equate | Value | Key | Equate | Value | Key | Equate | Value |
|---|---|---|---|---|---|---|---|---|
| [Y=] | kYEqu | $49 | [MODE] | kMode | $45 | [X,T,θ,n] | kVarX | $B4 |
| [WINDOW] | kWindow | $48 | [DEL] | kDel | $0A | [STAT] | kStat | $31 |
| [ZOOM] | kZoom | $2E | < | kLeft | $02 | V | kDown | $04 |
| [TRACE] | kTrace | $5A | Λ | kUp | $03 | |||
| [GRAPH] | kGraph | $44 | > | kRight | $01 | |||
| [MATH] | kMath | $32 | [x-1] | kInv | $86 | [x2] | kSquare | $BD |
| [APPS] | kAppsMenu | $2C | [SIN] | kSin | $B7 | [,] | kComma | $8B |
| [PRGM] | kPrgm | $2D | [COS] | kCos | $B9 | [(] | kLParen | $85 |
| [VARS] | kVars | $35 | [TAN] | kTan | $BB | [)] | kRParen | $86 |
| [CLEAR] | kClear | $09 | [^] | kExpon | 84 | [÷] | kDiv | $83 |
| [LOG] | kLog | $C1 | [LN] | kLn | $BF | [STO=>] | kStore | $8A |
| [7] | k7 | $95 | [4] | k4 | $92 | [1] | k1 | $8F |
| [8] | k8 | $96 | [5] | k5 | $93 | [2] | k2 | $90 |
| [9] | k9 | $97 | [6] | k6 | $94 | [3] | k3 | $91 |
| [×] | kMul | $82 | [-] | kSub | $81 | [+] | kAdd | $80 |
| [0] | k0 | $8E | ||||||
| [.] | kDecPnt | $8D | ||||||
| [(-)] | kChs | $8C | ||||||
| [ENTER] | kEnter | $05 | ||||||
Second-Function Keys
[edit | edit source]| Key | Equate | Value | Key | Equate | Value | Key | Equate | Value |
|---|---|---|---|---|---|---|---|---|
| [STAT PLOT] | kStatEd | $43 | [QUIT] | kQuit | $40 | [LINK] | kLinkIO | $41 |
| [TBLSET] | kTblSet | $4B | [INS] | kIns | $0B | [LIST] | kList | $3A |
| [FORMAT] | kFormat | $57 | [2nd] + < | kBOL | $0E | |||
| [CALC] | kCalc | $3B | [2nd] + > | kEOL | $0F | |||
| [TABLE] | kTable | $4A | ||||||
| [TEST] | kTest | $33 | [MATRX] | kMatrix | $37 | [Ö`] | kSqrt | $BE |
| [ANGLE] | kAngle | $39 | [SIN-1] | kASin | $B8 | [EE] | kEE | $98 |
| [DRAW] | kDraw | $2F | [COS-1] | kACos | $BA | [{] | kLBrace | $EC |
| [DISTR] | kDist | $38 | [TAN-1] | kATan | $BC | [}] | kRBrace | $ED |
| [p] | kPi | $B5 | [e] | kCONSTeA | $EF | |||
| [10x] | kALog | $C2 | [ex] | kExp | $C0 | [RCL] | kRecall | $0C |
| [u] | kUnA | $F9 | [L4] | kL4A | $F6 | [L1] | kL1A | $F3 |
| [v] | kVnA | $FA | [L5] | kL5A | $F7 | [L2] | kL2A | $F4 |
| [w] | kWnA | $FB | [L6] | kL6A | $F8 | [L3] | kL3A | $F5 |
| [[] | kLBrack | $87 | []] | kRBrack | $88 | [MEM] | kMem | $36 |
| [OFF] | kOff | $3F | ||||||
| [CATALOG] | kCatalog | $3E | ||||||
| [i] | kI | $EE | ||||||
| [ANS] | kAns | $C5 | ||||||
| [ENTRY] | kLastEnt | $0D | ||||||
Alpha-Function Keys
[edit | edit source]| Key | Equate | Value | Key | Equate | Value | Key | Equate | Value |
|---|---|---|---|---|---|---|---|---|
| Page Up | kAlphaUp | $07 | [A] | kCapA | $9A | [D] | kCapD | $9D |
| Page Down | kAlphaDown | $08 | [B] | kCapB | $9B | [E] | kCapE | $9E |
| [C] | kCapC | $9C | [F] | kCapF | $9F | |||
| [G] | kCapG | $A0 | ||||||
| [H] | kCapH | $A1 | ||||||
| [I] | kCapI | $A2 | [N] | kCapN | $A7 | [S] | kCapS | $AC |
| [J] | kCapJ | $A3 | [O] | kCapO | $A8 | [T] | kCapT | $AD |
| [K] | kCapK | $A4 | [P] | kCapP | $A9 | [U] | kCapU | $AE |
| [L] | kCapL | $A5 | [Q] | kCapQ | $AA | [V] | kCapV | $AF |
| [M] | kCapM | $A6 | [R] | kCapR | $AB | [W] | kCapW | $B0 |
| [X] | kCapX | $B1 | ||||||
| [Y] | kCapY | $B2 | [_] | kSpace | $99 | |||
| [Z] | kCapZ | $B3 | [:] | kColon | $C6 | |||
| [θ] | kThetA | $CC | [?] | kQuest | $CA | |||
| ["] | kQuotE | $CB | [SOLVE] | kAlphaEnter | $06 | |||
Alpha-Alpha-Function Keys
| Key | Equate | Value | Key | Equate | Value | Key | Equate | Value |
|---|---|---|---|---|---|---|---|---|
| [a] | kLa | $E2 | [d] | kLd | $E5 | [i] | kLi | $EA |
| [b] | kLb | $E3 | [e] | kLe | $E6 | [j] | kLj | $EB |
| [c] | kLc | $E4 | [f] | kLf | $E7 | [k] | kLk | $EC |
| [g] | kLg | $E8 | [l] | kLl | $ED | |||
| [h] | kLh | $E9 | [m] | kLm | $EE | |||
| [n] | kLSmalln | $EF | [s] | kLs | $F4 | [x] | kLx | $F9 |
| [o] | kLo | $F0 | [t] | kLt | $F5 | [y] | kLy | $FA |
| [p] | kLp | $F1 | [u] | kLu | $F6 | [z] | kLz | $FB |
| [q] | kLq | $F2 | [v] | kLv | $F7 | |||
| [r] | kLSmallr | $F3 | [w] | kLw | $F8 | |||
GetCSC (Scan Key) Codes
[edit | edit source]These KeyCodes are returned from the B_Call(_GetSCS) call. Note that the [APPS] key is equated to skMatrix for portability to the TI-83.
| Key | Equate | Value | Key | Equate | Value | Key | Equate | Value |
|---|---|---|---|---|---|---|---|---|
| [Y=] | skYEqu | $35 | [2nd] | sk2nd | $36 | [ALPHA] | skAlpha | $30 |
| [WINDOW] | skWindow | $34 | [MODE] | skMode | $37 | [X,T,θ,n] | skGraphVar | $28 |
| [ZOOM] | skZoom | $33 | [DEL] | skDel | $38 | [STAT] | skStat | $20 |
| [TRACE] | skTrace | $32 | < | skLeft | $02 | V | skDown | $01 |
| [GRAPH] | skGraph | $31 | Λ | skUp | $04 | > | skRight | $03 |
| [MATH] | skMath | $2F | [x-1] | skRecip | $2E | [x2] | skSquare | $2D |
| [APPS] | skMatrix | $27 | [SIN] | skSin | $26 | [,] | skComma | $25 |
| [PRGM] | skPrgm | $1F | [COS] | skCos | $1E | [(] | skLParen | $1D |
| [VARS] | skVars | $17 | [TAN] | skTan | $16 | [)] | skRParen | $15 |
| [CLEAR] | skClear | $0F | [^] | skPower | $0E | [÷] | skDiv | $0D |
| [LOG] | skLog | $2C | [LN] | skLn | $2B | [STO=>] | skStore | $2A |
| [7] | sk7 | $24 | [4] | sk4 | $23 | [1] | sk1 | $22 |
| [8] | sk8 | $1C | [5] | sk5 | $1B | [2] | sk2 | $1A |
| [9] | sk9 | $14 | [6] | sk6 | $13 | [3] | sk3 | $12 |
| [×] | skMul | $0C | [-] | skSub | $0B | [+] | skAdd | $0A |
| [0] | sk0 | $21 | ||||||
| [.] | skDecPnt | $19 | ||||||
| [(-)] | skChs | $11 | ||||||
| [ENTER] | skEnter | $09 | ||||||