Structural Biochemistry/Carnot Cycle
Introduction
[edit | edit source]The Carnot Cycle describes the thermodynamic cycle where heat is transferred to energy. This cycle follow four reversible steps: (1) isothermal expansion, (2) adiabatic expansion, (3) isothermal compression, and (4) adiabatic compression. This allows for a positive net work due to two properties of the cycle: reversibility and the largest possible heat transfer between the hottest reservoir to the coldest reservoir. This is shown in the following figures and table:


According to this figure, heat is transferred from the hot reservoir T(1) to the engine shown by Q(1). Q(1) and Q(2) are opposite in signs because the efficiency of the heat engine is the total amount of heat that enters the system minus the total amount of heat that leaves the system.
For the figure on the right, the P-T diagram of the heat engine shows that the total amount of work is the difference between the area of the top curve and the bottom curve. It also shows that the efficiency of heat transferred of the heat engine cannot be 100% according to the Second Law of Thermodynamics. The following equations show the efficiency of a heat engine which was used to derive the second law of spontaniety.
which can also be shown in two other ways:
or
The P-T diagram of the carnot cycle could be broken down into four steps according to the table below. From step 1 to step 2 there is an isothermal expansion which means that the internal energy, is equal to zero. This leaves q = -w, and the work of the first isothermal expansion could be calculated. Following up, there is an adiabatic expansion where the heat transfer, q, is equal to zero showing that
whereas from step 2 to 3 and then 4 there is an isothermal expansion and then an adiabatic expansion respectively. The equations are shown in the table.

Source: Castellan, Gilbert W. Physical Chemistry. 3rd Ed. Menlo Park: Addison-Wesley P C, 1983.
Biochemistry: Role of Thermodynamic Cycle in Transition-State Theory
[edit | edit source]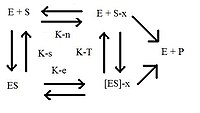
According to the transition-state theory, enzymes are flexible protein molecules that can catalyze molecules that go through stages of transition-state between initial and final conformations. The transition-state of the substrate, or the "half-chair" conformation, binds more reactively to the enzyme than the ground or final state (refer to transition state for more details). This recent theory is called transition-state stabilization. Using x-ray crystallography and the mutagenesis methods, or alteration of the enzymes' amino acid, has help gain more knowledge of transition-state stabilization.
The theory is base off two assumptions that the reaction is dynamically bottlenecked and that it acts in equilibrium. The general equation for this theory is
where k is the rate-reaction constant, is the transmission coefficient, is the frequency, and
is the equilibrium constant. The constant, is just the correction factor for the extraneous factors that affect the rate-reaction.
Using the figure shown, the two rate-reactions for both enzyme and enzyme transition state are compared,
where the subscripts e and n refer to enzymic and non-enzymic activity respectively. Since is the same as the catalysis rate-constant in the simplest form, the equation could be expressed using the dissociation constant and the transition state constant as
Since the rate of enzyme reactions are great, the proportion is typically to . The proportion could be dropped from the equation because it is not likely to deviate enzyme to non-enzyme rate-reactions by much. Therefore, the final equation is derived:
showing that the transition state binds at a greater power than that of the ground state substrate.
Reference
[edit | edit source]Kraut, Joseph. "How Do Enzymes Work?" Research Articles. Professor of University of California, San Diego. Published in October 1988.




















