Sensory Systems/Computer Models/NeuralSimulation
Simulating Action Potentials
[edit | edit source]Action Potential
[edit | edit source]The "action potential" is the stereotypical voltage change that is used to propagate signals in the nervous system.

With the mechanisms described below, an incoming stimulus (of any sort) can lead to a change in the voltage potential of a nerve cell. Up to a certain threshold, that's all there is to it ("Failed initiations" in Fig. 4). But when the Threshold of voltage-gated ion channels is reached, it comes to a feed-back reaction that almost immediately completely opens the Na+-ion channels ("Depolarization" below): This reaches a point where the permeability for Na+ (which is in the resting state is about 1% of the permeability of K+) is 20\*larger than that of K+. Together, the voltage rises from about -60mV to about +50mV. At that point internal reactions start to close (and block) the Na+ channels, and open the K+ channels to restore the equilibrium state. During this "Refractory period" of about 1 m, no depolarization can elicit an action potential. Only when the resting state is reached can new action potentials be triggered.
To simulate an action potential, we first have to define the different elements of the cell membrane, and how to describe them analytically.
Cell Membrane
[edit | edit source]The cell membrane is made up by a water-repelling, almost impermeable double-layer of proteins, the cell membrane. The real power in processing signals does not come from the cell membrane, but from ion channels that are embedded into that membrane. Ion channels are proteins which are embedded into the cell membrane, and which can selectively be opened for certain types of ions. (This selectivity is achieved by the geometrical arrangement of the amino acids which make up the ion channels.) In addition to the Na+ and K+ ions mentioned above, ions that are typically found in the nervous system are the cations Ca2+, Mg2+, and the anions Cl- .
States of ion channels
[edit | edit source]Ion channels can take on one of three states:
- Open (For example, an open Na-channel lets Na+ ions pass, but blocks all other types of ions).
- Closed, with the option to open up.
- Closed, unconditionally.
Resting state
[edit | edit source]The typical default situation – when nothing is happening - is characterized by K+ that are open, and the other channels closed. In that case two forces determine the cell voltage:
- The (chemical) concentration difference between the intra-cellular and extra-cellular concentration of K+, which is created by the continuous activity of the ion pumps described above.
- The (electrical) voltage difference between the inside and outside of the cell.
The equilibrium is defined by the Nernst-equation:
R ... gas-constant, T ... temperature, z ... ion-valence, F ... Faraday constant, [X]o/i … ion concentration outside/ inside. At 25° C, RT/F is 25 mV, which leads to a resting voltage of
With typical K+ concentration inside and outside of neurons, this yields . If the ion channels for K+, Na+ and Cl- are considered simultaneously, the equilibrium situation is characterized by the Goldman-equation
where Pi denotes the permeability of Ion "i", and I the concentration. Using typical ion concentration, the cell has in its resting state a negative polarity of about -60 mV.
Activation of Ion Channels
[edit | edit source]The nifty feature of the ion channels is the fact that their permeability can be changed by
- A mechanical stimulus (mechanically activated ion channels)
- A chemical stimulus (ligand activated ion channels)
- Or an by an external voltage (voltage gated ion channels)
- Occasionally ion channels directly connect two cells, in which case they are called gap junction channels.
Important
- Sensory systems are essentially based ion channels, which are activated by a mechanical stimulus (pressure, sound, movement), a chemical stimulus (taste, smell), or an electromagnetic stimulus (light), and produce a "neural signal", i.e. a voltage change in a nerve cell.
- Action potentials use voltage gated ion channels, to change the "state" of the neuron quickly and reliably.
- The communication between nerve cells predominantly uses ion channels that are activated by neurotransmitters, i.e. chemicals emitted at a synapse by the preceding neuron. This provides the maximum flexibility in the processing of neural signals.
Modeling a voltage dependent ion channel
[edit | edit source]Ohm's law relates the resistance of a resistor, R, to the current it passes, I, and the voltage drop across the resistor, V:
or
where is the conductance of the resistor. If you now suppose that the conductance is directly proportional to the probability that the channel is in the open conformation, then this equation becomes
where is the maximum conductance of the cannel, and is the probability that the channel is in the open conformation.
Example: the K-channel
Voltage gated potassium channels (Kv) can be only open or closed. Let α be the rate the channel goes from closed to open, and β the rate the channel goes from open to closed
Since n is the probability that the channel is open, the probability that the channel is closed has to be (1-n), since all channels are either open or closed. Changes in the conformation of the channel can therefore be described by the formula
Note that α and β are voltage dependent! With a technique called "voltage-clamping", Hodgkin and Huxley determine these rates in 1952, and they came up with something like
If you only want to model a voltage-dependent potassium channel, these would be the equations to start from. (For voltage gated Na channels, the equations are a bit more difficult, since those channels have three possible conformations: open, closed, and inactive.)
Hodgkin Huxley equation
[edit | edit source]The feedback-loop of voltage-gated ion channels mentioned above made it difficult to determine their exact behaviour. In a first approximation, the shape of the action potential can be explained by analyzing the electrical circuit of a single axonal compartment of a neuron, consisting of the following components: 1) Na channel, 2) K channel, 3) Cl channel, 4) leakage current, 5) membrane capacitance, :
The final equations in the original Hodgkin-Huxley model, where the currents in of chloride ions and other leakage currents were combined, were as follows:

where , , and are time- and voltage dependent functions which describe the membrane-permeability. For example, for the K channels n obeys the equations described above, which were determined experimentally with voltage-clamping. These equations describe the shape and propagation of the action potential with high accuracy! The model can be solved easily with open source tools, e.g. the Python Dynamical Systems Toolbox PyDSTools. A simple solution file is available under [1] , and the output is shown below.
Links to full Hodgkin-Huxley model
[edit | edit source]Modeling the Action Potential Generation: The Fitzhugh-Nagumo model
[edit | edit source]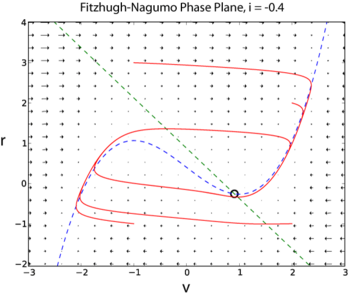
The Hodgkin-Huxley model has four dynamical variables: the voltage , the probability that the K channel is open, , the probability that the Na channel is open given that it was closed previously, , and the probability that the Na channel is open given that it was inactive previously, . A simplified model of action potential generation in neurons is the Fitzhugh-Nagumo (FN) model. Unlike the Hodgkin-Huxley model, the FN model has only two dynamic variables, by combining the variables and into a single variable , and combining the variables and into a single variable
The following two examples are taken from I is an external current injected into the neuron. Since the FN model has only two dynamic variables, its full dynamics can be explored using phase plane methods (Sample solution in Python here [2])
Simulating a Single Neuron with Positive Feedback
[edit | edit source]The following two examples are taken from [3] . This book provides a fantastic introduction into modeling simple neural systems, and gives a good understanding of the underlying information processing.
Let us first look at the response of a single neuron, with an input , and with feedback onto itself. The weight of the input is , and the weight of the feedback . The response of the neuron is given by
This shows how already very simple simulations can capture signal processing properties of real neurons.

""" Simulation of the effect of feedback on a single neuron """
import numpy as np
import matplotlib.pylab as plt
# System configuration
is_impulse = True # 'True' for impulse, 'False' for step
t_start = 11 # set a start time for the input
n_steps = 100
v = 1 # input weight
w = 0.95 # feedback weight
# Stimulus
x = np.zeros(n_steps)
if is_impulse:
x[t_start] = 1 # then set the input at only one time point
else:
x[t_start:] = 1 # step input
# Response
y = np.zeros(n_steps) # allocate output vector
for t in range(1, n_steps): # at every time step (skipping first)
y[t] = w*y[t-1] + v*x[t-1] # compute the output
# Plot the results
time = np.arange(n_steps)
fig, axs = plt.subplots(2, 1, sharex=True)
axs[0].plot(time, x)
axs[0].set_ylabel('Input')
axs[0].margins(x=0)
axs[1].plot(time, y)
axs[1].set_xlabel('Time Step')
axs[1].set_ylabel('Output')
plt.show()
Simulating a Simple Neural System
[edit | edit source]Even very simple neural systems can display a surprisingly versatile set of behaviors. An example is Wilson's model of the locust-flight central pattern generator. Here the system is described by
W is the connection matrix describing the recurrent connections of the neurons, and describes the input to the system.


""" 'Recurrent' feedback in simple network:
linear version of Wilson's locust flight central pattern generator (CPG) """
import numpy as np
import matplotlib.pylab as plt
# System configuration
v = np.zeros(4) # input weight matrix (vector)
v[1] = 1
w1 = [ 0.9, 0.2, 0, 0] # feedback weights to unit one
w2 = [-0.95, 0.4, -0.5, 0] # ... to unit two
w3 = [ 0, -0.5, 0.4, -0.95] # ... to unit three
w4 = [ 0, 0, 0.2, 0.9 ] # ... to unit four
W = np.vstack( [w1, w2, w3, w4] )
n_steps = 100
# Initial kick, to start the system
x = np.zeros(n_steps) # zero input vector
t_kick = 11
x[t_kick] = 1
# Simulation
y = np.zeros( (4,n_steps) ) # zero output vector
for t in range(1,n_steps): # for each time step
y[:,t] = W @ y[:,t-1] + v * x[t-1] # compute output
# Show the result
time = np.arange(n_steps)
plt.plot(time, x, '-', label='Input')
plt.plot(time, y[1,:], ls='dashed', label = 'Left Motorneuron')
plt.plot(time, y[2,:], ls='dotted', label='Right Motorneuron')
# Format the plot
plt.xlabel('Time Step')
plt.ylabel('Input and Unit Responses')
plt.gca().margins(x=0)
plt.tight_layout()
plt.legend()
plt.show()
The Development and Theory of Neuromorphic Circuits
[edit | edit source]Introduction
[edit | edit source]Neurmomorphic engineering uses very-large-scale-integration (VLSI) systems to build analog and digital circuits, emulating neuro-biological architecture and behavior. Most modern circuitry primarily utilizes digital circuit components because they are fast, precise, and insensitive to noise. Unlike more biologically relevant analog circuits, digital circuits require higher power supplies and are not capable of parallel computing. Biological neuron behaviors, such as membrane leakage and threshold constraints, are functions of material substrate parameters, and require analog systems to model and fine tune beyond digital 0/1. This paper will briefly summarize such neuromorphic circuits, and the theory behind their analog circuit components.
Current Events in Neuromorphic Engineering
[edit | edit source]In the last 10 years, the field of neuromorphic engineering has experienced a rapid upswing and received strong attention from the press and the scientific community.
After this topic came to the attention of the EU Commission, the Human Brain Project was launched in 2013, which was funded with 600 million euros over a period of ten years. The aim of the project is to simulate the human brain from the level of molecules and neurons to neural circuits. It is scheduled to end in September 2023, and although the main goal has not been achieved, it is providing detailed 3D maps of at least 200 brain regions and supercomputers to model functions such as memory and consciousness, among other things [4]. Another major deliverable is the EBRAINS virtual platform, launched in 2019. It provides a set of tools and image data that scientists worldwide can use for simulations and digital experiments.
Also in 2013, the U.S. National Institute of Health announced funding announced funding for the BRAIN project aimed at reconstructing the activity of large populations of neurons. It is ongoing and $680 million in funding has been allocated through 2023.
Other major accomplishments in recent years are listed below
1. TrueNorth Chip (IBM, 2014): with a total number of 268 million programmable synapses
2. Loihi Chip (Intel, 2017): based on asynchronous neural spiking network (SNN) for adaptive event-driven parallel computing. It was superseded by Loihi2 in 2021.
3. prototype chip (IMEC, 2017): first self-learning neuromorphic chip based on OxRAM technology
4. Akida AI Processor Development Kits (Brainchip, 2021): 1st commercially available neuromorphic processor
Transistor Structure & Physics
[edit | edit source]Metal-oxide-silicon-field-effect-transistors (MOSFETs) are common components of modern integrated circuits. MOSFETs are classified as unipolar devices because each transistor utilizes only one carrier type; negative-type MOFETs (nFETs) have electrons as carriers and positive-type MOSFETs (pFETs) have holes as carriers.
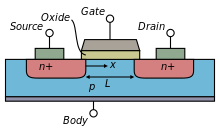
The general MOSFET has a metal gate (G), and two pn junction diodes known as the source (S) and the drain (D) as shown in Fig \ref{fig: transistor}. There is an insulating oxide layer that separates the gate from the silicon bulk (B). The channel that carries the charge runs directly below this oxide layer. The current is a function of the gate dimensions.
The source and the drain are symmetric and differ only in the biases applied to them. In a nFET device, the wells that form the source and drain are n-type and sit in a p-type substrate. The substrate is biased through the bulk p-type well contact. The positive current flows below the gate in the channel from the drain to the source. The source is called as such because it is the source of the electrons. Conversely, in a pFET device, the p-type source and drain are in a bulk n-well that is in a p-type substrate; current flows from the source to the drain.
When the carriers move due to a concentration gradient, this is called diffusion. If the carriers are swept due to an electric field, this is called drift. By convention, the nFET drain is biased at a higher potential than the source, whereas the source is biased higher in a pFET.
In a nFET, when a positive voltage is applied to the gate, positive charge accumulates on the metal contact. This draws electrons from the bulk to the silicon-oxide interface, creating a negatively charged channel between the source and the drain. The larger the gate voltage, the thicker the channel becomes which reduces the internal resistance, and thus increases the current logarithmically. For small gate voltages, typically below the threshold voltage, , the channel is not yet fully conducting and the increase in current from the drain to the source increases linearly on a logarithmic scale. This regime, when , is called the subthreshold region. Beyond this threshold voltage, , the channel is fully conducting between the source and drain, and the current is in the superthreshold regime.

For current to flow from the drain to the source, there must initially be an electric field to sweep the carriers across the channel. The strength of this electric field is a function of the applied potential difference between the source and the drain (), and thus controls the drain-source current. For small values of , the current linearly increases as a function of for constant values. As increases beyond , the current saturates.
pFETs behave similarly to nFET except that the carriers are holes, and the contact biases are negated.
In digital applications, transistors either operate in their saturation region (on) or are off. This large range in potential differences between the on and off modes is why digital circuits have such a high power demand. Contrarily, analog circuits take advantage of the linear region of transistors to produce a continuous signals with a lower power demand. However, because small changes in gate or source-drain voltages can create a large change in current, analog systems are prone to noise.
The field of neuromorphic engineering takes advantage of the noisy nature of analog circuits to replicate stochastic neuronal behavior [5] [6]. Unlike clocked digital circuits, analog circuits are capable of creating action potentials with temporal dynamics similar to biological time scales (approx. ). The potentials are slowed down and firing rates are controlled by lengthening time constants through leaking biases and variable resistive transistors. Analog circuits have been created that are capable of emulating biological action potentials with varying temporal dynamics, thus allowing silicon circuits to mimic neuronal spike-based learning behavior [7]. Whereas, digital circuits can only contain binary synaptic weights [0,1], analog circuits are capable of maintaining synaptic weights within a continuous range of values, making analog circuits particularly advantageous for neuromorophic circuits.
Basic static circuits
[edit | edit source]With an understanding of how transistors work and how they are biased, basic static analog circuits can be rationalized through. Afterward, these basic static circuits will be combined to create neuromorphic circuits. In the following circuit examples, the source, drain, and gate voltages are fixed, and the current is the output. In practice, the bias gate voltage is fixed to a subthreshold value (), the drain is held in saturation (), and the source and bulk are tied to ground (, ). All non-idealities are ignored.

Diode-Connected Transistor
[edit | edit source]A diode-connected nFET has its gate tied to the drain. Since the floating drain controls the gate voltage, the drain-gate voltages will self-regulate so the device will always sink the input current, . Beyond several microvolts, the transistor will run in saturation. Similarly, a diode-connected pFET has its gate tied to the source. Though this simple device seems to merely function as a short circuit, it is commonly used in analog circuits for copying and regulating current. Particularly in neuromorphic circuits, they are used to slow current sinks, to increase circuit time constants to biologically plausible time regimes.
Current Mirror
[edit | edit source]A current mirror takes advantage of the diode-connected transistor’s ability to sink current. When an input current is forced through the diode connected transistor, , the floating drain and gate are regulated to the appropriate voltage that allows the input current to pass. Since the two transistors share a common gate node, will also sink the same current. This forces the output transistor to duplicate the input current. The output will mirror the input current as long as:
- .
The current mirror gain can be controlled by adjusting these two parameters. When using transistors with different dimensions, otherwise known as a tilted mirror, the gain is:
A pFET current mirror is simply a flipped nFET mirror, where the diode-connected pFET mirrors the input current, and forces the other pFET to source output current.
Current mirrors are commonly used to copy currents without draining the input current. This is especially essential for feedback loops, such as the one use to accelerate action potentials, and summing input currents at a synapse.
Source Follower
[edit | edit source]A source follower consists of an input transistor, , stacked on top of a bias transistor, . The fixed subthreshold () bias voltage controls the gate , forcing it to sink a constant current, . is thus also forced to sink the same current () regardless of what the input voltage, .
A source follower is called so because the output, , will follow with a slight offset described by:
where kappa is the subthreshold slope factor, typically less than one.
This simple circuit is often used as a buffer. Since no current can flow through the gate, this circuit will not draw current from the input, an important trait for low-power circuits. Source followers can also isolate circuits, protecting them from power surges or static. A pFET source follower only differs from an nFET source follower in that the bias pFET has its bulk tied to .
In neuromorphic circuits, source followers and the like are used as simple current integrators which behave like post-synaptic neurons collecting current from many pre-synaptic neurons.
Inverter
[edit | edit source]An inverter consists of a pFET, , stacked on top of a nFET, , with their gates tied to the input, and the output is tied to the common source node, . When a high signal is input, the pFET is off but the nFET is on, effectively draining the output node, , and inverting the signal. Contrarily, when the input signal is low, the nFET is off but the pFET is on, charging up the node.
This simple circuit is effective as a quick switch. The inverter is also commonly used as a buffer because an output current can be produced without directly sourcing the input current, as no current is allowed through the gate. When two inverters are used in series, they can be used as a non-inverting amplifier. This was used in the original Integrate-and-Fire silicon neuron by Mead et al., 1989 to create a fast depolarizing spike similar to that of a biological action potential [8]. However, when the input fluctuates between high and low signals both transistors are in superthreshold saturation draining current, making this a very power hungry circuit.
Current Conveyor
[edit | edit source]The current conveyor is also commonly known as a buffered current mirror. Consisting of two transistors with their gates tied to a node of the other, the Current Conveyor self regulates so that the output current matches the input current, in a manner similar to the Current Mirror.
The current conveyor is often used in place of current mirrors for large serially repetitious arrays. This is because the current mirror current is controlled through the gate, whose oxide capacitance will result in a delayed output. Though this lag is negligible for a single output current mirror, long mirroring arrays will accumulative significant output delays. Such delays would greatly hinder large parallel processes such as those that try to emulate biological neural network computational strategies.
Differential Pair
[edit | edit source]The differential pair is a comparative circuit composed of two source followers with a common bias that forces the current of the weaker input to be silenced. The bias transistor will force to remain constant, tying the common node, , to a fixed voltage. Both input transistors will want to drain current proportional to their input voltages, and , respectively. However, since the common node must remain fixed, the drains of the input transistors must raise in proportion to the gate voltages. The transistor with the lower input voltage will act as a choke and allow less current through its drain. The losing transistor will see its source voltage increase and thus fall out of saturation.
The differential pair, in the setting of a neuronal circuit, can function as an activation threshold of an ion channel below which the voltage-gated ion channel will not open, preventing the neuron from spiking [9].
Silicon neurons
[edit | edit source]Winner-Take-All
[edit | edit source]The Winner-Take-All (WTA) circuit, originally designed by Lazzaro et al. [10], is a continuous time, analog circuit. It compares the outputs of an array of cells, and only allows the cell with the highest output current to be on, inhibiting all other competing cells.

Each cell comprises a current-controlled conveyor, and receives input currents, and outputs into a common line controlling a bias transistor. The cell with the largest input current, will also output the largest current, increasing the voltage of the common node. This forces the weaker cells to turn off. The WTA circuit can be extended to include a large network of competing cells. A soft WTA also has its output current mirrored back to the input, effectively increasing the cell gain. This is necessary to reduce noise and random switching if the cell array has a small dynamic range.
WTA networks are commonly used as a form of competitive learning in computational neural networks that involve distributed decision making. In particular, WTA networks have been used to perform low level recognition and classification tasks that more closely resemble cortical activity during visual selection tasks [11].
Integrate & Fire Neuron
[edit | edit source]The most general schematic of an Integrate & Fire Neuron, is also known as an Axon-Hillock Neuron, is the most commonly used spiking neuron model [8]. Common elements between most Axon-Hillock circuits include: a node with a memory of the membrane potential , an amplifier, a positive feedback loop , and a mechanism to reset the membrane potential to its resting state, .
The input current, , charges the , which is stored in a capacitor, C. This capacitor is analogous to the lipid cellular membrane which prevents free ionic diffusion, creating the membrane potential from the accumulated charge difference on either side of the lipid membrane. The input is amplified to output a voltage spike. A change in membrane potential is positively fed back through to , producing a faster spike. This closely resembles how a biological axon hillock, which is densely packed with voltage-gated sodium channels, amplifies the summed potentials to produce an action potential. When a voltage spike is produced, the reset bias, , begins to drain the node. This is similar to sodium-potassium channels which actively pump sodium and potassium ions against the concentration gradient to maintain the resting membrane potential.


The original Axon Hillock silicon neuron has been adapted to include an activation threshold with the addition of a Differential Pair comparing the input to a set threshold bias [9]. This conductance-based silicon neuron utilizes differential-pair integrator (DPI) with a leaky transistor to compare the input, to the threshold, . The leak bias , refractory period bias , adaptation bias , and positive feed back gain, all independently control the spiking frequency. Research has been focused on implementing spike frequency adaptation to set refractory periods and modulating thresholds [12]. Adaptation allows for the neuron to modulate its output firing rate as a function of its input. If there is a constant high frequency input, the neuron will be desensitized to the input and the output will be steadily diminished over time. The adaptive component of the conductance-based neuron circuit is modeled through the calcium flux and stores the memory of past activity through the adaptive capacitor, . The advent of spike frequency adaptation allowed for changes on the neuron level to control adaptive learning mechanisms on the synapse level. This model of neuronal learning is modeled from biology [13] and will be further discussed in Silicon Synapses.
Silicon Synapses
[edit | edit source]The most basic silicon synapse, originally used by Mead et al.,1989 [8], simply consists of a pFET source follower that receives a low signal pulse input and outputs a unidirectional current, [14].

The amplitude of the spike is controlled by the weight bias, , and the pulse width is directly correlated with the input pulse width which is set by $V_{\tau}$. The capacitor in the Lazzaro et al. (1993) synapse circuit was added to increase the spike time constant to a biologically plausible value. This slowed the rate at which the pulse hyperpolarizes and depolarizes, and is a function of the capacitance.

For multiple inputs depicting competitive excitatory and inhibitive behavior, the log-domain integrator uses and to regulate the output current magnitude, , as function of the input current, , according to:
controls the rate at which is able to charge the output transistor gate. governs the rate in which the output is sunk. This competitive nature is necessary to mimic biological behavior of neurotransmitters that either promote or depress neuronal firing.
Synaptic models have also been developed with first order linear integrators using log-domain filters capable of modeling the exponential decay of excitatory post-synaptic current (EPSC) [15]. This is necessary to have biologically plausible spike contours and time constants. The gain is also independently controlled from the synapse time constant which is necessary for spike-rate and spike-timing dependent learning mechanisms.

The aforementioned synapses simply relay currents from the pre-synaptic sources, varying the shape of the pulse spike along the way. They do not, however, contain any memory of previous spikes, nor are they capable of adapting their behavior according to temporal dynamics. These abilities, however, are necessary if neuromorphic circuits are to learn like biological neural networks.

According to Hebb's postulate, behaviors like learning and memory are hypothesized to occur on the synaptic level [16]. It accredits the learning process to long-term neuronal adaptation in which pre- and post-synaptic contributions are strengthened or weakened by biochemical modifications. This theory is often summarized in the saying, "Neurons that fire together, wire together." Artificial neural networks model learning through these biochemical "wiring" modifications with a single parameter, the synaptic weight, . A synaptic weight is a parameter state variable that quantifies how a presynaptic neuron spike affects a postsynaptic neuron output. Two models of Hebbian synaptic weight plasticity include spike-rate-dependent plasticity (SRDP), and spike-timing-dependent plasticity (STDP). Since the conception of this theory, biological neuron activity has been shown to exhibit behavior closely modeling Hebbian learning. One such example is of synaptic NMDA and AMPA receptor plastic modifications that lead to calcium flux induced adaptation [17].
Learning and long-term memory of information in biological neurons is accredited to NMDA channel induced adaptation. These NMDA receptors are voltage dependent and control intracellular calcium ion flux. It has been shown in animal studies that neuronal desensitization is diminished when extracellular calcium was reduced [17].

Since calcium concentration exponentially decays, this behavior easily implemented on hardware using subthreshold transistors. A circuit model demonstrating calcium dependent biological behavior is shown by Rachmuth et al. (2011) [18]. The calcium signal, , regulates AMPA and NMDA channel activity through the node according to calcium-dependent STDP and SRDP learning rules. The output of these learning rules is the synaptic weight, , which is proportional to the number of active AMPA and NMDA channels. The SRDP model describes the weight in terms of two state variables, , which controls the update rule, and , which controls the learning rate.
where is the synaptic weight, is the update rule, is the learning rate, and is a constant that allows the weight to drift out of saturation in absence of an input.
The NMDA channel controls the calcium influx, . The NMDA receptor voltage-dependency is modeled by , and the channel mechanics are controlled with a large capacitor to increase the calcium time constant, . The output is copied via current mirrors into the and circuits to perform downstream learning functions.
The circuit compares to threshold biases, and ), that respectively control long-term potentiation or long-term depression through a series of differential pair circuits. The output of differential pairs determines the update rule. This circuit has been demonstrated to exhibit various Hebbian learning rules as observed in the hippocampus, and anti-Hebbian learning rules used in the cerebellum.
The circuit controls when synaptic learning can occur by only allowing updates when is above a differential pair set threshold, . The learning rate (LR) is modeled according to:
where is a function of and controls the learning rate, is the capacitance of the circuit, and is the threshold voltage of the comparator. This function demonstrates that must be biased to maintain an elevated in order to simulate SRDT. A leakage current, , was included to drain to during inactivity.
The NEURON simulation environment
[edit | edit source]Introduction
[edit | edit source]Neuron is a simulation environment with which you can simulate the propagation of ions and action potentials in biological and artificial neurons as well as in networks of neurons [19]. The user can specify a model geometry by defining and connecting neuron cell parts, which can be equipped with various mechanisms such as ion channels, clamps and synapses. To interact with NEURON the user can either use the graphical user interface (GUI) or one of the programming languages hoc (a language with a C like syntax) or Python as an interpreter. The GUI contains a wide selection of the most-used features, an example screenshot is shown in the Figure on the right. The programming languages on the other hand can be exploited to add more specific mechanisms to the model and for automation purposes Furthermore, custom mechanisms can be created with the programming language NMODL, which is an extension to MODL, a model description language developed by the NBSR (National Biomedical Simulation Resource). These new mechanisms can then be compiled, and added to models through the GUI or interpreters.
Neuron was initially developed by John W. Moore at Duke university in collaboration with Michael Hines. It is currently used in numerous institutes and universities for educational and research purposes. There is an extensive amount of information available including the official website containing the documentation, the NEURON forum and various tutorials and guides. Furthermore in 2006 the authoritative reference book for NEURON was published called “The NEURON Book” [20]. To read the following chapters and to work with NEURON, some background knowledge on the physiology of neurons is recommended. Some examples of information sources about neurons are the WikiBook chapter, or the videos in the introduction of the Advanced Nervous System Physiology chapter on Khan academy. We will not cover specific commands or details about how to perform the here mentioned actions with NEURON since this document is not intended to be a tutorial but only an overview of the possibilities and model structure within NEURON. For more practical information on the implementation with NEURON I would recommend the tutorials which are linked below and the documentation on the official webpage [19].
Model creation
[edit | edit source]
Single Cell Geometry
[edit | edit source]First we will discuss the creation of a model geometry that consists of a single biological neuron. A schematic representation of a Neuron is shown in the Figure on the right. In the following Listing an example code snippet is shown in which a multi-compartment cell with one soma and two dendrites is specified using hoc.
load_file("nrngui.hoc")
// Create a soma object and an array containing 2 dendrite objects
ndend = 2
create soma, dend[ndend]
access soma
// Initialize the soma and the dendrites
soma {
nseg = 1
diam = 18.8
L = 18.8
Ra = 123.0
insert hh
}
dend[0] {
nseg = 5
diam = 3.18
L = 701.9
Ra = 123
insert pas
}
dend[1] {
nseg = 5
diam = 2.0
L = 549.1
Ra = 123
insert pas
}
// Connect the dendrites to the soma
connect dend[0](0), soma(0)
connect dend[1](0), soma(1)
// Create an electrode in the soma
objectvar stim
stim = new IClamp(0.5)
// Set stimulation parameters delay, duration and amplitude
stim.del = 100
stim.dur = 100
stim.amp = 0.1
// Set the simulation end time
tstop = 300
Sections
[edit | edit source]The basic building blocks in NEURON are called “sections”. Initially a section only represents a cylindrical tube with individual properties such as the length and the diameter. A section can be used to represent different neuron parts, such as a soma, a dendrite or an axon, by equipping it with the corresponding mechanisms such as ion channels or synapse connections with other cells or artificial stimuli. A neuron cell can then be created by connecting the ends of the sections together however you want, for example in a tree like structure, as long as there are no loops. The neuron as specified in the Listing above, is visualized in the Figure on the right.
Segments
[edit | edit source]In order to model the propagation of action potentials through the sections more accurately, the sections can be divided into smaller parts called “segments”. A model in which the sections are split into multiple segments is called a “multi-compartment” model. Increasing the number of segments can be seen as increasing the granularity of the spatial discretization, which leads to more accurate results when for example the membrane properties are not uniform along the section. By default, a section consists of one segment.
Membrane Mechanisms
[edit | edit source]The default settings of a section do not contain any ion channels, but the user can add them [21]. There are two types of built-in ion channel membrane mechanisms available, namely a passive ion channel membrane model and a Hodgkin-Huxley model membrane model which represents a combination of passive and voltage gated ion channels. If this is not sufficient, users can define their own membrane mechanisms using the programming language NMODL.
Point Processes
[edit | edit source]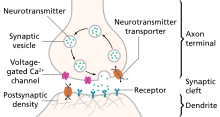
Besides membrane mechanisms which are defined on membrane areas, there are also local mechanisms known as “Point processes” that can be added to the sections. Some examples are synapses, as shown in the Figure on the right, and voltage- and current clamps. Again, users are free to implement their own mechanisms with the programming language NMODL. One key difference between point processes and membrane mechanisms is that the user can specify the location where the point process should be added onto the section, because it is a local mechanism [21].
Output and Visualizations
[edit | edit source]The computed quantities can be tracked over time and plotted, to create for example a graph of voltage versus time within a specific segment, as shown in the GUI screenshot above. It is also possible to make animations, to show for example how the voltage distribution within the axon develops over time. Note that the quantities are only computed at the centre of each segment and at the boundaries of each section.
Creating a Cell Network
[edit | edit source]Besides modeling the ion concentrations within single cells it is also possible to connect the cells and to simulate networks of neurons. To do so the user has to attach synapses, which are point processes, to the postsynaptic neurons and then create “NetCon” objects which will act as the connection between the presynaptic neuron and the postsynaptic neuron. There are different types of synapses that the user can attach to neurons, such as AlphaSynapse, in which the synaptic conductance decays according to an alpha function and ExpSyn in which the synaptic conductance decays exponentially. Like with other mechanisms it is also possible to create custom synapses using NMODL. For the NetCon object it is possible to specify several parameters, such as the threshold and the delay, which determine the required conditions for the presynaptic neuron to cause a postsynaptic potential.
Artificial Neurons
[edit | edit source]Besides the biological neurons that we have discussed up until now, there is also another type of neuron that can be simulated with NEURON known as an “artificial” neuron. The difference between the biological and artificial neurons in NEURON is that the artificial neuron does not have a spatial extent and that its kinetics are highly simplified. There are several integrators available to model the behaviour of artificial cells in NEURON, which distinguish themselves by the extent to which they are simplifications of the dynamics of biological neurons [22]. To reduce the computation time for models of artificial spiking neuron cells and networks, the developers of NEURON have chosen to support event-driven simulations. This substantially reduced the computational burden of simulating spike-triggered synaptic transmissions. Although modelling conductance based neuron cells requires a continuous system simulation, NEURON can still exploit the benefits of event-driven methods for networks that contain biological and artificial neurons by fully supporting hybrid simulations. This way any combination of artificial and conductance based neuron cells can be simulated while still achieving the reduced computation time that results from event-driven simulation of artificial cells [23]. The user can also add other artificial neuron classes with the language NMODL.
Neuron with Python
[edit | edit source]
Since 1984 NEURON has provided the hoc interpreter for the creation and execution of simulations. The hoc language has been extended and maintained to be used with NEURON up until now, but because this maintenance takes a lot of time and because it has turned out to be an orphan language limited to NEURON users, the developers of NEURON desired a more modern programming language as an interpreter for NEURON. Because Python has become widely used within the area of scientific computing with many users creating packages containing reusable code, it is now more attractive as an interpreter than hoc[24]. There are three ways to use NEURON with Python. The first way is to run NEURON with the terminal accepting interactive Python commands. The second way is to run NEURON with the interpreter hoc, and to access Python commands through special commands in hoc. The third way is to use NEURON as an extension module for Python, such that a NEURON module can be imported into Python or IPython scripts.
Installation
[edit | edit source]To use the first and second mode, so to use NEURON with Python embedded, it is sufficient to complete the straightforward installation. To use the third mode however, which is NEURON as an extension module for Python, it is necessary to build NEURON from the source code and install the NEURON shared library for Python which is explained in this installation guide.
NEURON commands in Python
[edit | edit source]Because NEURON was originally developed with hoc as an interpreter the user still has to explicitly call hoc functions and classes from within Python. All functions and classes that have existed for hoc are accessible in Python through the module “neuron”, both when using Python embedded in NEURON or when using NEURON as an extension module. There are only some minor differences between the NEURON commands in hoc and Python so there should not be many complications for users when changing from one to another [24]. There are a couple of advantages of using NEURON with Python instead of hoc. One of the primary advantages is that Python offers a lot more functionality because it is a complete object-oriented language and because there is an extensive suite of analysis tools available for science and engineering. Also, loading user-defined mechanisms from NMODL scripts has become easier, which makes NEURON more attractive for simulations of very specific mechanisms [24]. More details on NEURON in combination with Python can be found here.
Tutorials
[edit | edit source]
There are multiple tutorials available online for getting started with NEURON and two of them are listed below.
In the first tutorial you will start with learning how to create a single compartment cell and finish with creating a network of neurons as shown in the Figure on the right, containing custom cell mechanisms. Meanwhile you will be guided through the NEURON features for templates, automation, computation time optimization and extraction of resulting data. The tutorial uses hoc commands but the procedures are almost the same within Python.
The second tutorial shows how to create a cell with a passive cell membrane and a synaptic stimulus, and how to visualize the results with the Python module matplotlib.
Further Reading
[edit | edit source]Besides what is mentioned in this introduction to NEURON, there are many more options available which are continuously extended and improved by the developers. An extensive explanation of NEURON can be found in “The NEURON book” [20], which is the official reference book. Furthermore the official website contains a lot of information and links to other sources as well.
References
[edit | edit source]Two additional sources are "An adaptive silicon synapse", by Chicca et al. [25] and "Analog VLSI: Circuits and Principles", by Liu et al. [26].
- ↑ T. Haslwanter (2012). "Hodgkin-Huxley Simulations [Python]". private communications.
- ↑ T. Haslwanter (2012). "Fitzhugh-Nagumo Model [Python]". private communications.
- ↑ T. Anastasio (2010). "Tutorial on Neural systems Modeling".
- ↑ Europe spent €600 million to recreate the human brain in a computer. How did it go?
- ↑
E Aydiner, AM Vural, B Ozcelik, K Kiymac, U Tan (2003), A simple chaotic neuron model: stochastic behavior of neural networks
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ WM Siebert (1965), Some implications of the stochastic behavior of primary auditory neurons
- ↑
G Indiveri, F Stefanini, E Chicca (2010), Spike-based learning with a generalized integrate and fire silicon neuron
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ a b c CA Mead (1989), Analog VLSI and Neural Systems
- ↑ a b RJ Douglas, MA Mahowald (2003), Silicon Neuron
- ↑
J Lazzaro, S Ryckebusch, MA Mahowald, CA Mead (1989), Winner-Take-All: Networks of Complexity
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ M Riesenhuber, T Poggio (1999), Hierarchical models of object recognition in cortex
- ↑
E Chicca, G Indiveri, R Douglas (2004), An event-based VLSI network of Integrate-and-Fire Neurons
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑
G Indiveri, E Chicca, R Douglas (2004), A VLSI reconfigurable network of integrate-and-fire neurons with spike-based learning synapses
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ J Lazzaro, J Wawrzynek (1993), Low-Power Silicon Neurons, Axons, and Synapses
- ↑
S Mitra, G Indiveri, RE Cummings (2010), Synthesis of log-domain integrators for silicon synapses with global parametric control
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ DO Hebb (1949), The organization of behavior
- ↑ a b
PA Koplas, RL Rosenberg, GS Oxford (1997), The role of calcium in the densensitization of capsaisin responses in rat dorsal root ganglion neurons
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑
G Rachmuth, HZ Shouval, MF Bear, CS Poon (2011), A biophysically-based neuromorphic model of spike rate-timing-dependent plasticity
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ a b Neuron, for empirically-based simulations of neurons and networks of neurons
- ↑ a b Nicholas T. Carnevale, Michael L. Hines (2009), The NEURON book
- ↑ a b NEURON Tutorial 1
- ↑ M.L. Hines and N.T. Carnevale (2002), The NEURON Simulation Environment
- ↑
Romain Brette, Michelle Rudolph, Ted Carnevale, Michael Hines, David Beeman, James M. Bower, Markus Diesmann, Abigail Morrison, Philip H. Goodman, Frederick C. Harris, Jr., Milind Zirpe, Thomas Natschläger, Dejan Pecevski, Bard Ermentrout, Mikael Djurfeldt, Anders Lansner, Olivier Rochel, Thierry Vieville, Eilif Muller, Andrew P. Davison, Sami El Boustani, Alain Destexhe (2002), Simulation of networks of spiking neurons: A review of tools and strategies
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ a b c
Hines ML, Davison AP, Muller E. NEURON and Python. Frontiers in Neuroinformatics. 2009;3:1. doi:10.3389/neuro.11.001.2009. (2009), NEURON and Python
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑
E Chicca, G Indiveri, R Douglas (2003), An adaptive silicon synapse
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑
SC Liu, J Kramer, T Delbrück, G Indiveri, R Douglas (2002), Analog VLSI: Circuits and Principles
{{citation}}: CS1 maint: multiple names: authors list (link)
![{\displaystyle {{E}_{X}}={\frac {RT}{zF}}\ln {\frac {{[X]}_{o}}{{[X]}_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e2d5c294b8784f463d80357bd660f5e515b23a8)
![{\displaystyle {{E}_{X}}={\frac {25mV}{z}}\log {\frac {{[X]}_{o}}{{[X]}_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49ea1afb0f8c662cb48929a3da01c5acdd4d6f88)

![{\displaystyle {{V}_{m}}={\frac {RT}{F}}\ln {\frac {{{P}_{K}}{{[{{K}^{+}}]}_{o}}+{{P}_{Na}}{{[N{{a}^{+}}]}_{o}}+{{P}_{Cl}}{{[Cl-]}_{i}}}{{{P}_{K}}{{[{{K}^{+}}]}_{i}}+{{P}_{Na}}{{[N{{a}^{+}}]}_{i}}+{{P}_{Cl}}{{[Cl-]}_{o}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a99888fc4b3f0858a0551a76f813fa566c3c7e2)


















































































![{\displaystyle dw=\eta ([Ca_{2+}])\cdot (\Omega ([Ca_{2+}])-\lambda w),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c904f8985f83bcc0f7cfbb240a97f5b6db16b3e)
![{\displaystyle \Omega ([Ca_{2+}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8365820f3ba6b3eb8631a0bb5ce819be1ec17d1)
![{\displaystyle \eta ([Ca_{2+}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9d4224f92cfee5905b380eb00eff81b77a2fe12)






![{\displaystyle \tau _{LR}\sim {\frac {\theta _{\eta }\cdot C_{\eta }}{I_{\eta }\cdot [Ca_{2+}]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20bac65985bece7edd0e340742a5312609aa49b9)
![{\displaystyle [Ca_{2+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4caea324562bc2c0bd11d4c73ed9eea47405b55)






