SA NC Doing Investigations/Chapter 7
Materials developed by the winning educators
[edit | edit source]This resource book is not meant to be a textbook on investigations with pages of ideas for teachers. Any examples given are intended to illustrate how even the most common classroom activities can be done with an investigative bias. The materials here, taken from the portfolios of winners of the MSTotY 2003 demonstrate this clearly. The first activity is the investigation of "fractions" for Intermediate Phase learners. Because it tackles the topic using measurement it is appropriate to both science and mathematics. The second and third activities are common in FET physics (Newton's Second Law and the electromagnetic motor rule). The reader will appreciate that by re-shaping them ever so slightly, even familiar activities can conform to the requirements of an "investigative approach." We might assume that "to investigate" means learners working alone and researching private topics that catch their imaginations. But this is not necessarily the case and activities with a specific focus and educator-directed can also be investigations.
In the first of the three examples learners are given a sequence of activities that follow the logic of fractions and learners study them through measurements. Indeed, measurement itself is an important aspect of investigation. So instead of talking about the "free investigation of private topics" by learners, which is the pure form, we now have what is an "investigative approach" to teaching and learning. Free investigations by learners are a special subset of the investigative approach. The important point is that whether learners follow their own curiosity or are led through a logical sequence by their educator, in both cases they are investigating in a way that follows the logic and nature of mathematics and science. The advantage of educator-led investigations is that learners can be shown a logical approach (e.g. asking and then answering a key question before moving to the next stage) even if it may not be as neat and sequenced in "the real world". By gaining this guided experience learners should adopt a similar approach in their free investigations. The first investigation was produced by Vanessa Thayer, winner of the 2003 award for Maths and Science Educator of the Year. Vanessa acknowledges the original inspiration for the activity and the source of some of the content. It is important for professionals to do this as they, of all people, must be above plagiarism and the unacknowledged use of other people's ideas. Using decimetres to investigate fractions: an investigation into fractions and measurement
SPECIAL NOTE All activities in this module were adapted from teaching material and ideas received at the in-service course for Intermediate Phase mathemaics educators at WCED, Cape Teaching Institute.
Guideline notes for the educator
[edit | edit source]The history of fractions
[edit | edit source]Early Egyptians made mention of fractions even before the pyramids were built, over 4000 years ago. Measurement was used to survey farms. They first used their elbows and fingers, but this did not work too well because elbows and fingers were of different lengths for different people.
In their quest for accuracy, they used standard units as equal parts of a bigger unit, e.g. the decimetre ruler. However, they now found that they had a whole bag of rulers, which was also inconvenient. So they later used tenths, hundredths, thousandths (decimals) but had to keep to common fractions (halves and quarters) and couldn't, for instance, measure of a metre in decimals. (Take the learners back in time and make the context real.)
We teach fractions to provide a basis for decimal fractions. We deliberately investigate common fractions in the context of measurement to allow learners the opportunity to discover the context within which fractions started and, most importantly, to see the logic behind equivalent, simple, mixed fractions etc and the relationship between common fractions and decimals. In this way learners are able to formulate their own rules / methods and will also, in the higher grades, understand the logic behind rules, methods and formulae.
The module of activities offer many opportunities for learners to talk about what they have done and engage with other learners and this is an effective way of making learners aware of how they are learning, building on their communication skills and most importantly, engaging with logic.
Try not to rush the concrete support of using the rulers. In this way learners will internalise the logic and will later be confident in working with abstract contexts. Ensure that the learners get the fraction language correct. Encourage them to say, e.g. 3 quarters and not 3 over 4. In the next module of activities, learners will have the opportunity of working with fractions in many other, varied contexts.
Assessment Plan Learning Area: Mathematics, RNCS Grade 5 Learning Outcome: L 01: Number, Operations and Relationships L 04: Measurement
Phase Learning Pathway
[edit | edit source]Grade 4
[edit | edit source]- Recognises and represents common fractions with different denominators including halves, thirds, quarters, fifths, sixths, sevenths, eighths, in order to describe and compare them.
- Recognises and uses equivalent forms of common fractions with denominators that are multiples of each other and decimal fractions of the form 0.5 2,5 etc. in the context of measurement.
Grade 5
[edit | edit source]- Recognises and represents common fractions to at least twelfths in order to describe and compare them.
- Recognises and uses equivalent forms of common fractions with denominators that are multiples of each other and decimal fractions of the form 0.5 2,5 etc. in the context of measurement.
Grade 6
[edit | edit source]- Recognises and represents common fractions including specifically tenths, hundredths, and percentages.
- Recognises and uses equivalent forms of common fractions with 1 digit or 2 digit denominator
- Decimal fractions to at least 2 decimal places
- Percentages
Grade 7
[edit | edit source]- Recognises, classifies and represents decimals (to at least 3 decimal places), fractions and percentages.
- Recognises and uses equivalent forms of rational numbers including common fractions, decimals, percentages
Baseline assessment task
[edit | edit source]Intended Outcome: The learner will be able to demonstrate an understanding of "an hour" in fraction notation. Method: Pen and Paper Technique: Worksheet Assessment Tool: Assessment Grid
The exit assessment task
[edit | edit source]Intended Outcome: The learner will be able to recognize, represent, describe, compare and convert between equivalent forms of common fractions in the context of measurement. Method: Pen and Paper Technique: Worksheet Assessment Tool: The rubric below, using four achievement level descriptors.
Formative assessment task
[edit | edit source][LO1: Number, operations and relationships L 04: Measurement] Grade assessment standard: The learner will be able to recognize, represent, describe, compare and convert between equivalent forms of common fractions in the context of measurement.
RUBRIC for Using Decimetres to Investigate Fractions.
[edit | edit source]|
RUBRIC for Using Decimetres to Investigate Fractions. | ||||
|---|---|---|---|---|
|
ASSESSMENT CRITERIA |
4 Exemplary Achievement |
3 Achieved Required Standard |
2 Partially Achieved Standard |
2 Partially Achieved Standard |
|
A. Representing common fractions |
Great attention is given to accuracy and details of measurement. |
The dark and light sheet are correctly drawn, fraction measurements for each sheet is given. |
At least one of the sheets is correctly represented. |
None of the sheets is correctly represented. |
|
B. Recognising Common Fractions |
The thickness's of the light and dark sheet are recognised no errors made |
The thickness's of the light and dark sheets are recognised using most rulers |
The thickness's of the light and dark sheet are recognised using some rulers |
No evidence that rulers were used correctly to recognise fractions |
|
C. Converting between equivalent forms of fractions |
All the equivalent rulers predicted to measure sample sheets A-E are correct |
Most of the equivalent rulers predicted to measure sample sheets A-E are correct |
Some of the equivalent rulers predicted to measure sample sheets A-E are correct |
Almost none of the equivalent rulers predicted to measure sample sheets A-E are correct |
|
D. Comparing fractions |
All the fractions units are arranged accurately from smallest to largest |
Most fraction units of rulers are arranged accurately from smallest to largest |
Evidence to show that learner can arrange the rulers from smallest to largest but with some difficulty |
None of the rulers is arranged accurately from smallest to largest. |
|
E. Describing common fractions ( using correct fraction notation) |
All of the fractions are described in correct fraction notation ( in the context of measurement) |
Most of the fractions are described in correct fraction (in the context of measurement) |
Some fractions are described in correct fraction notation without the context of measurement |
There is no evidence to show that the fraction notation is understood |
Reporting Code: Comments:
________________________________________________________________________________
________________________________________________________________________________
|
Signature: Parent/Guardian |
Date |
Educator's Signature |
Learner materials
[edit | edit source]Measuring with decimeters
[edit | edit source]Put your ordinary rulers away. You will only work with the special rulers provided here.
You will use the decimetre as a unit. Here you can see approximately how long a decimetre is:
|
|
Task 1
[edit | edit source]1. Cut out a strip of paper as long as the "practice decimetre" above. Now you have made a "one decimetre ruler" for yourself.
2. Use your practice ruler to check whether the pencil below is exactly 2 decimetre long. If not, is it more than or less than or about (approximately) 2 decimetres long?
3. Measure the length and the width of the marble slab below with your practice decimetre. Is it a square?
4. Measure the edges of your desk top with your practice decimetre.
5. Was it possible to measure your desk top accurately with the practice decimetre ruler? Discuss this with a friend.
[Use the next two pages as photocopy masters or as exemplars, if they are copied. Make sure that Rulers ABCD, EFGH and JKMN are all exactly 20cm when they have been photocopied. The pages may require a slight enlargement. If you redraw them make sure that the sub-divisions are all exactly equal in any one ruler. For example, all the small sub-divisions in Ruler D must be exactly 1cm long.]
[KEY: E (30ths), F (15ths), G (24ths), H (16ths), J (20ths), K (25ths), M (40ths), N (50ths)]
Task 2
[edit | edit source]Cut out the ruler (with Rulers A, B, C and D on it) and fold it along the dotted lines. In this way you will make your own set of decimetre ruler.
1. How long is each small part on the lower section of ruler B? Write down your answer.
2. How long is each small part on the lower section of ruler C? Write down your answer.
3. How long is each small part on the lower section of ruler D? Write down your answer.
Simphiwe has measured each of the pencils on the next page. Here are his results:
- Pencil A is a bit less than 1.5 decimetres long.
- Pencil B is about halfway between 1.5 decimetres and 2 decimetres long
- Pencil C is precisely 2 decimetres long.
- Pencil D is a bit less than 2 decimetres long.
- Pencil E is precisely 1.5 decimetres long.
- Pencil F is precisely halfway between 1.5 decimetres and 2 decimetres long.
- Pencil G is a bit more than 2 decimetres long.
4. Use your new decimetre ruler to check each of Simphiwe's measurements. When you have completed your measurements, compare your findings with your group.
Mr. Marota tried to measure this earthworm.
First he tried to measure it with the tenths-ruler:
Can you see that the tenths-ruler does not work well for this worm? You can only say that the worm is a bit longer than 6 tenths of a decimetre, and shorter than 7 tenths of a decimetre.
Then Mr. Marota tried a twelfths-ruler:
Next he tried the eighths-ruler:
Mr. Marota was very happy now. He had succeeded in measuring the earthworm quite accurately. He wrote: The earthworm is 5 eighths of a decimetre long.
Task 3
[edit | edit source]1. How long is the earthworm below?
2. Measure each of the pencils below. For each pencil you must find the ruler that fits exactly. In each case write your answer down like Mr Marta did.
Task 4
[edit | edit source]1. Measure pencils B, E and F accurately using your new rulers.
2. Compare your results with your group.
3. Work alone again. Use one of your rulers to draw a line exactly 7 tenths of a decimetre long.
4. Use one of your rulers to draw a line exactly 5 sixteenths of a decimetre long.
5. Explain to your group how you managed to do Question 4.
6. Use one of your rulers to draw a line exactly 17 twentieths of a decimetre long.
Equivalent Fractions
Smaller parts
Simphiwe wants to investigate how fish grow when they get different kinds of food. So he wants to measure this little fish accurately.
Simphiwe tries all the different decimetre rulers that he has.
Task 5
[edit | edit source]1. Can Simphiwe now say accurately how long the fish is?
2. Ben says the fish is 9 twelfths of a decimetre long. Do you agree?
3. Make two new decimetre rulers, one by cutting out and folding Ruler EFGH and the other by cutting out and folding Ruler JKMN. 4. For each new ruler, count the small sub-divisions of a decimetre and write on the ruler what fraction of a decimetre the y are e.g. Ruler E (30ths).
4. Measure the fish above accurately with Ruler EFGH. Write down your answer.
'The language of fractions (equivalent fractions)
Task 6
[edit | edit source]Measure these fish accurately using Rulers EFGH and JKMN. Write down your best answer like this: Fish X is 19 twenty fourths of a dm.
Compare your results with your group.
Equivalent Fractions: Different descriptions of the same length
Settling a disagreement
Tswanelo and Simphiwe disagree about the lengths of fishes D, F and G. Here are Tswanelo's results:
- Fish D is 3 quarters of a decimetre long.
- Fish F is 8 tenths of a decimetre long.
- Fish G is 21 twenty-fourths of a decimetre long.
Here are Simphiwe's results:
- Fish D is 15 twentieths of a decimetre long.
- Fish F is 16 twentieths of a decimetre long.
- Fish G is 7 eighths of a decimetre long.
Task 7
[edit | edit source]Work on your own. 1. Using all of your decimetre rulers, investigate the situation regarding the lengths of fishes D, F and G.
2. Write a letter to Tswanelo and Simphiwe, to help them to resolve their differences. (Group work)
This is how Tswanelo measured Fish D.
Tswanelo sees that he can describe the length of Fish D in two ways. He can say it is 3 quarters of a decimetre.
He can also say it is 6 eighths of a decimetre.
3. Can one also measure Fish D with other rulers?
Simphiwe sees that Fish D can also be measured more accurately using twelfths of a decimetre. Write down the fish's length in twelfths of a decimetre.
4. Vuyo says: Fish D is 4 12 sixths of a decimetre long. Is he correct?
5. Explain in writing why 3 quarters of a decimetre and 9 twelfths of a decimetre are actually the same length. Compare your explanation with your group.
6. Work on your own again. Explain in writing why 4 12 sixths of a decimetre and 9 twelfths of a decimetre are actually the same length. Compare your explanations within your group.
Task 8
[edit | edit source]Equivalent Fraction problems
1. Use your rulers to check if 15 twentieths of a decimetre is the same length as 9 twelfths of a decimetre? Write down the reason for your answer.
2. Compare your response to question 6 with your group.
3. If Fish C is 23 thirtieths of a decimetre long, do you think it can be measured more accurately in sixtieths of a decimetre? First think about it by yourself and come to your conclusion, do not discuss this with your group just yet.
4. A certain Fish X is precisely 3 fifths of a decimetre long. Write down all the other ways that you can describe the length of Fish X accurately.
5. Compare your answers with your group.
6. Another fish, Fish Y is precisely 10 sixteenths of a decimetre long. Write down all the other ways that you can describe the length of Fish Y accurately.
7. Compare your answers with your group.
Combining parts
Houses are sometimes built with cement building sheets instead of bricks. The cement sheets that are made in factories are not all the same thickness. Since sheets of different thicknesses are used for different purposes and sold at different prices, it is sometimes necessary to measure the sheets quite carefully.
The cement sheet sample below is {frac}3/24 dm (three twenty-fourths of a decimetre) thick, as you can see.

Task 9
[edit | edit source]Measure the thickness of each of the following cement sheet samples. Use the decimetre rulers that you have cut out, and take trouble to make very accurate measurements.

Compare your answers with your group. You must reach agreement.
Task 10
[edit | edit source]Two or more sheets are sometimes joined to make one thicker sheet. You can see an example of this below. These combined sheets are called composite sheets. Measure the thickness of the dark and the light part of the composite sheet below. Make the most accurate measurements you can.

1. Using the twentieths ruler (Ruler J),
- measure the darker sheet:
- measurement _____________ dm.
- measure the lighter sheet:
- measurement _____________ dm
- measure the composite sheet:
- measurement _____________ dm
2. Using the twenty fourths ruler (Ruler G),
- measure the darker sheet:
- measurement _____________ dm.
- measure the lighter sheet:
- measurement _____________ dm
- measure the composite sheet:
- measurement _____________ dm
3. Working very accurately, draw your own composite sheet as follows:
- The total thickness of the composite sheet must be dm. (Use Ruler A)
- The darker sheet must be dm. (Shade it in.)
4. Give the thickness measurements of the darker, lighter and composite sheets in Number 3 using Rulers, A, E, D, F.
|
dm Ruler |
Lighter Sheet |
Darker Sheet |
|
A |
| |
|
E |
| |
|
D |
| |
|
F |
|
5. Examine all the measurements for your light sheet and compare them with the measurements for the dark sheet. Do you see a pattern? Write down what you notice.
6. Work in a group. Discuss how you can use this pattern to get the measurements of rulers A, E, D and F for your composite sheet without using rulers A, E, D and F.
7. What were the most important conclusions from your discussion? Write them down. ____________________________________________________________________________________________________________________________________ ____________________________________________________________________________________________________________________________________ ____________________________________________________________________________________________________________________________________
Use the logic of equivalent fractions to find a method for working out patterns.
Task 11: classroom assessment
[edit | edit source]Diane measures some samples of composite sheets and records her results. These are given in the table below. For each measurement show which other rulers could also be used to measure the sheet exactly. Write down the accurate measurement from that ruler in the columns. (Check your answers by comparing rulers. Place them next to one another to do this.)
Copy this table and write in your answers.
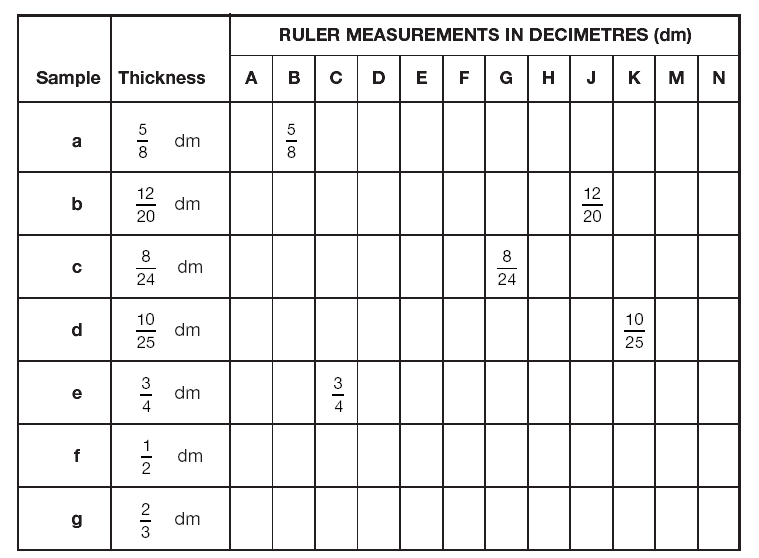
3. List all the fraction units on your rulers from largest to smallest. ____________________________________________________________________________ ____________________________________________________________________________
4. What went through your mind when you had written down the sequence? ____________________________________________________________________________ _____________________________________________________________________________
Tenths and hundredths.
This is a very fine decimetre ruler.

It is actually a tenths-ruler, but each tenth of a decimetre is again divided into 10 smaller units.
Task 12
[edit | edit source]1. How many small units are there in the above ruler?
2. Measure the thickness of all the sheet samples on the next page with one of your "old" decimetre fraction rulers (ABCD, EFGH or JKMN).
3. Now measure the sheet samples with your new (hundredths) ruler.
4. Calculate the thickness of each of the following composite sheets in two ways, first by adding your measurements in other fraction parts of a decimetre, and then by adding your measurements in hundredths of a decimetre.
|
|
Other fractions |
Other fractions |
|---|---|---|
|
A + C |
|
|
|
B + D |
|
|
|
A + D + E |
|
|
|
B + F |
|
|
|
A + E + F |
|
|
Using the Tenths and Hundredths Ruler

Group work: Discuss this task only when you have completed it.
1. Circle the rulers that made it easier to measure the thickness of the sheets a. our old dm rulers b. tenths and hundredths ruler
2. When we use the tenths and hundredths rulers to measure, we call this kind of fraction
- ____________________________.
3. Measure Sheet A (above) using your old dm ruler and your tenths and hundredths ruler. Write down the measurements in numbers and in words.
- _______________________________________________________________________
- _______________________________________________________________________
- _______________________________________________________________________
4. Why do you think the tenths and hundredths rulers were invented?
- _______________________________________________________________________
- _______________________________________________________________________
- _______________________________________________________________________
- _______________________________________________________________________
5. Do tenths and hundredths rulers do the same job as the old dm rulers?
- ______________
6. What is the difference between them? What is different?
- _______________________________________________________________________
- _______________________________________________________________________
- _______________________________________________________________________
Writing fractions using decimal notation - A different way to write fractions
Instead of writing 7/10, we can write 0,7. "0,7" is read as "nought comma seven", or just as "comma seven".
Instead of writing 7/100, we can write 0,07. This is read as "nought comma nought seven", or just as "comma nought seven".
Instead of writing 2 37/100, we can write 2,37. This is read as "two comma three seven".
This way of writing tenths and hundredths is called the decimal notation.
Task 13
[edit | edit source]1. Write each of the following lengths in the decimal notation and then find the sum of the lengths: a. 3 dm + 1/10 dm + 4/100 dm b. 1 dm + 7/10 dm + 4/100 dm c. 3 dm + 5/10 dm + 9/100 dm d. 3 dm + 5/10 dm e. 3 dm + 5/100 dm
2. With a partner or in a group, check your answers and compare the methods you used.
3. Arrange Sheet A-F from thickest to thinnest using your tenths / hundredths measurements.
4. Write down their thicknesses in decimetres using decimal notation.
5. Calculate the thickest composite sheet you could make from any two of these sheets and write down the thickness in decimetres and in decimal notation.
6. Calculate the thinnest composite sheet you could make from any two of these sheets and write down the thickness in decimetres and in decimal notation.
Task 14: Calculator Task
[edit | edit source]a. Enter ".2 + .05 =" and write the answer:
- __________
b. Write the answer to (a) as an ordinary fraction:
- __________
c. 25 hundredths is also equal to a ____ part of a decimetre. ( 1 1/10, 4/12, 3/4, 1/2, 1/4
d. Do the following calculations and write them out in the same way as in (a), (b) and (c) above:
- .7 + .05 = ___
- .3 + .45 = ___
- .12 + .13 = ___
- .2 + .55 = ___
- .38 + .12 = ___
FET Physics
[edit | edit source]The next activities cover two important topics in FET physics. They are presented in a very conventional form but, like the Intermediate Phase investigation of fractions, these activities can be taught in an investigative style. The difference is that if the educator's control is strong, the activity will be less of an investigation. If it is less educator-centred i.e. he/she gives more control over the activity to the learners, it will be more of an investigation way. Again we must make the point that the spirit of investigation lies largely in the approach taken by the individual educator to teaching and learning.
Newton's Second Law (NII)
[edit | edit source]Outcomes
[edit | edit source]At the end of the lesson, learners should be able to:
- Draw a graph of force versus acceleration and interpret it.
- State the relationship between acceleration of an object and the force producing the acceleration.
- Apply this relationship to their everyday life experiences
Teaching method
[edit | edit source]Experimental/investigative
Teaching aids
[edit | edit source]Ticker tape timer, ticker tape, metre rule, runway, books to support the runway, thin string, pulley, some 10g mass pieces, graph paper, worksheets, pencil, rubber, ruler, scientific calculator, chalk, board duster.
Tips
[edit | edit source]Most Grade 12 textbooks and practical worksheets suggest that when doing this investigation the force can be applied on the trolley with rubber bands or spring balances double or triple the force. Anyone who has tried this method will have found that it is very difficult to move along with the trolley while at the same time stretching one or two rubber bands to a constant length. This difficulty can be avoided by using mass pieces (i.e. "weights" as described) instead of rubber bands. Any identical objects, e.g. 10g mass pieces will do the trick.
- Tie a mass piece to a thin, strong thread.
- Use an oiled pulley. (See sketch above.)
- Start the ticker tape timer and then release the trolley. Prevent it from crashing.
- Increase the number of mass pieces one at a time and repeat the procedure until the trolley accelerates at too high a rate for useful results.
- Problems to overcome: ticker tape timer not making clear marks and the trolley running skew.
- Learners must grasp the concept under investigation AND the fact that experimental results are never "perfect".
- A runway for the trolley can be made from an old door.
Start of lesson
[edit | edit source]Divide learners into groups at most four learners per group.
Introduction
[edit | edit source]The educator draws this diagram on the chalkboard ... ... and asks: "What will happen to the object if the two forces act on it simultaneously?"
- (Anticipated answer: "The object will remain a rest because there in resultant force on it.")
The educator then draws another diagram ... ... and asks: "What will happen if these two forces are applied to the object?"
- (Anticipated answer: "The object will move to the right because there is a resultant force of 2N acting on it.")
The educator consolidates the answers by referring to previous knowledge: A body will, if at rest, remain at rest or, if moving, continue moving in a straight line at constant speed forever if there are no resultant forces acting on it. (NI)
The educator then writes the aim of the investigation on the chalkboard.

Aim
[edit | edit source]To investigate the effect on acceleration when mass is increased

Method
[edit | edit source]- The educator distributes prepared worksheets and describes the experimental procedure (no mention of "acceleration" at this point) including how the motion of the object can be determined from the ticker timer and tapes.
- Mention here that when there are sufficient data, these can be plotted on graphs.
- Learners gather around the table and observe the educator as he/she produces the first tape.
- Agree with the class on the series of masses to be used and let the learners produce the rest of the tapes for themselves.
- Agree on the method of finding the time interval between each dot on the tapes and calculate T.
- Learners now analyze each tape. (Discard the first few points and the last few points on the tapes and use the middle section.)
- NOTE: if ticker timers are not available it is possible to make ticker tapes with dots that can be analysed. While this is less than ideal to do it this it is certainly better than doing the activity purely as a textbook exercise.
- Learners calculate the average velocities for each interval (i.e. between dots on the tape) and record these on their worksheets.
- On the same sheet of graph paper?, plot graphs of velocity vs time for each tape and calculate the "rate change in velocity" for each tape (i.e. for varying masses).
- Ask questions that get the learners to understand that by varying the masses on the string, they have varied the force applied to the trolley.
- Introduce the concept of acceleration: the rate of change of velocity. Work out the units of acceleration.
- Express the slopes of the graphs on the series of v-t graphs as accelerations.
- Ask the question: "what is responsible for the acceleration of the trolley?"
- (Anticipated answer: "The changing force applied on the trolley by changing the
number of mass pieces.")
- Suggest drawing a graph to look for a relationship between force and acceleration. Plot the graph using "number of mass pieces" as the independent variable (x-axis) against the acceleration (y-axis).
- Is there a straight line relationship? Draw a "best fit" line (i.e. a line that goes closest to most points) on the acceleration vs resultant force graph.
Discussion
[edit | edit source]- Is there a straight line trend on the graph? (Carefully executed tests on this apparatus usually lead to one.)
- If not, what could affect the experimental procedure? (Friction will affect the size of the acceleration but since it is a force in the direction of movement it will not affect the linearity of the graph. The fact that friction varies with the velocity of the moving
object need not be discussed here since the affect is probably within the experimental error anyway.)
- The educator discusses the questions with the class and clarifies the meaning of a straight line graph relating acceleration to the resultant force. (10 min)
Conclusion
[edit | edit source]If there is a straight line trend this shows a linear relationship that can be stated:
- "a is proportional to 1/F"
- Explain that this is known as Newton's Second Law of motion and show the class the mathematical formulation including mass (of the trolley and NOT the number of mass pieces) as the constant (of proportionality).
Homework
[edit | edit source]Learners are asked to bring along written information about situations where the relationship between acceleration and force is evident in their everyday experiences/practical situations e.g. The difference between one and two people pushing a stalled car and the resultant accelerations.
Electromagnetism and electromagnetic forces
[edit | edit source]The beauty of this investigation, on electromagnetism, is that it is almost identical to the kind of investigations done by Michael Faraday in England and Joseph Henry in the USA in the early part of the nineteenth century. Their pioneering work has led to the great motors and generators that keep our industries moving today.
Outcomes
[edit | edit source]At the end of the lesson, learners should be able to:
- Apply Fleming's Left Hand Rule to determine the force experienced by an electrical conductor in a magnetic field.
- State and understand the factors which influence this force.
- Name practical, everyday applications of this force.
Teaching method
[edit | edit source]Learner investigation
Teaching aids
[edit | edit source]Retort stand, U-magnet, copper leads (x2), torch cells (x4), circuit board, copper pieces designed for this experiment.
Start of the lesson
[edit | edit source]The educator divides learners into 3 groups- at least 8 learners per group.
Introduction
[edit | edit source]The educator asks the following question: "What effects does the electrical current in a wire show? Describe any you have seen."
- (Anticipated answers: heating, lighting, magnetic and chemical effect.)
The educator starts with phenomena already known to the learners. Make no explanation at this point of the relationship between electric current and its magnetic effect
The educator writes the day's topic on the board. "Investigating forces on current-carrying conductors in magnetic fields."
Aim
[edit | edit source]To investigate the force experienced by a current carrying conductor in a magnetic field.
The educator issues worksheets, explains the apparatus (see diagrams below) for the investigation and allows the learners to follow the instructions.
Discussion
[edit | edit source]The educator discusses any effects of forces observed (i.e. movement  ­ see NII) and draws out learner observations/opinions on the variables affecting the observed forces e.g. increasing the magnetic field strength or increasing the length of the conductor in the magnetic field. Make a chalkboard summary and let learners note the additional information.
Apparatus
[edit | edit source]For this investigation, set up this apparatus using the suggested materials or others like them. The apparatus is not complicated and can be assembled using scrap or low costs materials.
NOTE: Magnets are easy to come by in the doors of discarded fridges. Old electrical flex and torch cells can also be found or bought very cheaply.
Obtain 3 metal wires, preferably copper and form them into the three shapes below.
Set up the apparatus for the investigation as shown in the diagram.
When electricity flows in the conducting wires, wire 1 must be able to move freely on the loop joints it makes with wires 2 and 3.
Apparatus for the investigation
[edit | edit source]Wire1 must be free to move into or out of the magnet as shown by the dotted arrows. Know which end of the U-magnet is its North pole.
Now connect the terminals of the battery to wires 2 ands 3 to complete the apparatus. (In a perfect world and with unlimited time, one would leave learners with the question  ­ "find the relationship among ... etc."  ­ and let them both design the apparatus to test the relationships and come up with answers. Unfortunately few educators can afford this luxury and so the apparatus for the investigation is a "given".)
Method and questions to answer by investigation
[edit | edit source]1. Set up the apparatus as shown in the diagrams.
2. Close the switch and note what happens to conductor 1.
3. What direction does the conductor move?
- ....................................................................................................
4. Change the polarity of your connections. i.e. positive and negative terminals. What direction does conductor 1 move now?
- ....................................................................................................
5. Will changing the polarity of the terminals affect the movement of the conductor?
- ....................................................................................................
6. Close the switch. Observe and note what happens.
- ....................................................................................................
7. Reverse the polarity of your magnetic field. Will this affect the movement of the conductor?
- ....................................................................................................
8. Are your observations in 2 Â ­ 7 consistent? Would you have expected what you observed? Respond and explain your response.
- ....................................................................................................
9. Draw diagrams that show the relationships between magnetic field direction (convention: North to South), the direction of the current in conductor 1 (convention: from positive to negative battery terminals) and the direction of the force on conductor 1.
10. Having drawn your explanatory diagrams (the three directions are all at right angles to one another i.e. the diagrams must show three dimensions: up-down on page left-right on page and into-out of page.)
11. With the diagrams complete, return to the apparatus and check the predictive value of your diagrams. Introduce Fleming's Left Hand Rule and let learners check the consistency of this rule with their diagrams.
12. Increase the number of cells in the circuit and note the deflection of conductor 1. Does it deflect more or less than when only one cell was used?
- ....................................................................................................
13. Is the direction of the force as you would have predicted it, even though current strength is increased?
- ....................................................................................................
14. Does the force experienced by the conductor increase or decrease when the number of cells is increased?
- ....................................................................................................
15. What can be concluded from this observation, given that increasing the number of cells also increases the current (Ohm' Law)
- ....................................................................................................
16. Draw a concept map and write an overall conclusion about the effect on a current- carrying conductor in a magnetic field.
- ....................................................................................................