This chapter deals with Poisson's equation

Provided that  , we will through distribution theory prove a solution formula, and for domains with boundaries satisfying a certain property we will even show a solution formula for the boundary value problem. We will also study solutions of the homogenous Poisson's equation
, we will through distribution theory prove a solution formula, and for domains with boundaries satisfying a certain property we will even show a solution formula for the boundary value problem. We will also study solutions of the homogenous Poisson's equation

The solutions to the homogenous Poisson's equation are called harmonic functions.
In section 2, we had seen Leibniz' integral rule, and in section 4, Fubini's theorem. In this section, we repeat the other theorems from multi-dimensional integration which we need in order to carry on with applying the theory of distributions to partial differential equations. Proofs will not be given, since understanding the proofs of these theorems is not very important for the understanding of this wikibook. The only exception will be theorem 6.3, which follows from theorem 6.2. The proof of this theorem is an exercise.
Theorem 6.2: (Divergence theorem)
Let  a compact set with smooth boundary. If
a compact set with smooth boundary. If  is a vector field, then
is a vector field, then

, where  is the outward normal vector.
is the outward normal vector.
Proof: See exercise 1.
Definition 6.5:
The Gamma function  is defined by
is defined by

The Gamma function satisfies the following equation:
Theorem 6.6:

Proof:


If the Gamma function is shifted by 1, it is an interpolation of the factorial (see exercise 2):
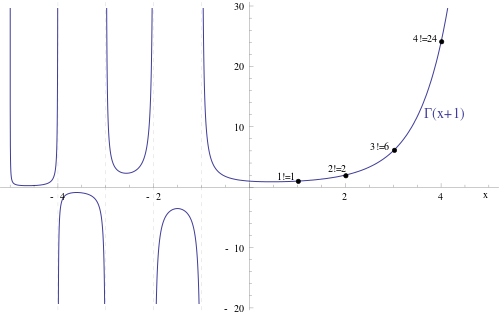
As you can see, in the above plot the Gamma function also has values on negative numbers. This is because what is plotted above is some sort of a natural continuation of the Gamma function which one can construct using complex analysis.
Definition and theorem 6.7:
The  -dimensional spherical coordinates, given by
-dimensional spherical coordinates, given by 

are a diffeomorphism. The determinant of the Jacobian matrix of  ,
,  , is given by
, is given by

Proof:
Proof:
The surface area and the volume of the  -dimensional ball with radius
-dimensional ball with radius  are related to each other "in a differential way" (see exercise 3).
are related to each other "in a differential way" (see exercise 3).
Proof:


We recall a fact from integration theory:
Lemma 6.11:  is integrable
is integrable 
 is integrable.
is integrable.
We omit the proof.
Theorem 6.12:
The function  , given by
, given by

is a Green's kernel for Poisson's equation.
We only prove the theorem for  . For
. For  see exercise 4.
see exercise 4.
Proof:
1.
We show that  is locally integrable. Let
is locally integrable. Let  be compact. We have to show that
be compact. We have to show that

is a real number, which by lemma 6.11 is equivalent to

is a real number. As compact in  is equivalent to bounded and closed, we may choose an
is equivalent to bounded and closed, we may choose an  such that
such that  . Without loss of generality we choose
. Without loss of generality we choose  , since if it turns out that the chosen
, since if it turns out that the chosen  is
is  , any
, any  will do as well. Then we have
will do as well. Then we have

For  ,
,

For  ,
,

, where we applied integration by substitution using spherical coordinates from the first to the second line.
2.
We calculate some derivatives of  (see exercise 5):
(see exercise 5):
For  , we have
, we have

For  , we have
, we have

For all  , we have
, we have

3.
We show that

Let  and
and  be arbitrary. In this last step of the proof, we will only manipulate the term
be arbitrary. In this last step of the proof, we will only manipulate the term  . Since
. Since  ,
,  has compact support. Let's define
has compact support. Let's define

Since the support of

, where  is the characteristic function of
is the characteristic function of  .
.
The last integral is taken over  (which is bounded and as the intersection of the closed sets
(which is bounded and as the intersection of the closed sets  and
and  closed and thus compact as well). In this area, due to the above second part of this proof,
closed and thus compact as well). In this area, due to the above second part of this proof,  is continuously differentiable. Therefore, we are allowed to integrate by parts. Thus, noting that
is continuously differentiable. Therefore, we are allowed to integrate by parts. Thus, noting that  is the outward normal vector in
is the outward normal vector in  of
of  , we obtain
, we obtain

Let's furthermore choose  . Then
. Then
 .
.
From Gauß' theorem, we obtain

, where the minus in the right hand side occurs because we need the inward normal vector. From this follows immediately that

We can now calculate the following, using the Cauchy-Schwartz inequality:



Now we define  , which gives:
, which gives:

Applying Gauß' theorem on  gives us therefore
gives us therefore


, noting that  .
.
We furthermore note that

Therefore, we have


due to the continuity of  .
.
Thus we can conclude that
 .
.
Therefore,  is a Green's kernel for the Poisson's equation for
is a Green's kernel for the Poisson's equation for  .
.
QED.
Theorem 6.12:
Let  be a function.
be a function.

Proof: We choose as an orientation the border orientation of the sphere. We know that for  , an outward normal vector field is given by
, an outward normal vector field is given by  . As a parametrisation of
. As a parametrisation of  , we only choose the identity function, obtaining that the basis for the tangent space there is the standard basis, which in turn means that the volume form of
, we only choose the identity function, obtaining that the basis for the tangent space there is the standard basis, which in turn means that the volume form of  is
is

Now, we use the normal vector field to obtain the volume form of  :
:

We insert the formula for  and then use Laplace's determinant formula:
and then use Laplace's determinant formula:

As a parametrisation of  we choose spherical coordinates with constant radius
we choose spherical coordinates with constant radius  .
.
We calculate the Jacobian matrix for the spherical coordinates:

We observe that in the first column, we have only the spherical coordinates divided by  . If we fix
. If we fix  , the first column disappears. Let's call the resulting matrix
, the first column disappears. Let's call the resulting matrix  and our parametrisation, namely spherical coordinates with constant
and our parametrisation, namely spherical coordinates with constant  ,
,  . Then we have:
. Then we have:



Recalling that

, the claim follows using the definition of the surface integral.
Theorem 6.13:
Let  be a function. Then
be a function. Then

Proof:
We have  , where
, where  are the spherical coordinates. Therefore, by integration by substitution, Fubini's theorem and the above formula for integration over the unit sphere,
are the spherical coordinates. Therefore, by integration by substitution, Fubini's theorem and the above formula for integration over the unit sphere,


Proof: Let's define the following function:

From first coordinate transformation with the diffeomorphism  and then applying our formula for integration on the unit sphere twice, we obtain:
and then applying our formula for integration on the unit sphere twice, we obtain:

From first differentiation under the integral sign and then Gauss' theorem, we know that

Case 1:
If  is harmonic, then we have
is harmonic, then we have

, which is why  is constant. Now we can use the dominated convergence theorem for the following calculation:
is constant. Now we can use the dominated convergence theorem for the following calculation:

Therefore  for all
for all  .
.
With the relationship

, which is true because of our formula for  , we obtain that
, we obtain that

, which proves the first formula.
Furthermore, we can prove the second formula by first transformation of variables, then integrating by onion skins, then using the first formula of this theorem and then integration by onion skins again:

This shows that if  is harmonic, then the two formulas for calculating
is harmonic, then the two formulas for calculating  , hold.
, hold.
Case 2:
Suppose that  is not harmonic. Then there exists an
is not harmonic. Then there exists an  such that
such that  . Without loss of generality, we assume that
. Without loss of generality, we assume that  ; the proof for
; the proof for  will be completely analogous exept that the direction of the inequalities will interchange. Then, since as above, due to the dominated convergence theorem, we have
will be completely analogous exept that the direction of the inequalities will interchange. Then, since as above, due to the dominated convergence theorem, we have

Since  is continuous (by the dominated convergence theorem), this is why
is continuous (by the dominated convergence theorem), this is why  grows at
grows at  , which is a contradiction to the first formula.
, which is a contradiction to the first formula.
The contradiction to the second formula can be obtained by observing that  is continuous and therefore there exists a
is continuous and therefore there exists a 

This means that since

and therefore

, that

and therefore, by the same calculation as above,

This shows (by proof with contradiction) that if one of the two formulas hold, then  is harmonic.
is harmonic.
Definition 6.16:
A domain is an open and connected subset of  .
.
For the proof of the next theorem, we need two theorems from other subjects, the first from integration theory and the second from topology.
Theorem 6.17:
Let  and let
and let  be a function. If
be a function. If

then  for almost every
for almost every  .
.
Theorem 6.18:
In a connected topological space, the only simultaneously open and closed sets are the whole space and the empty set.
We will omit the proofs.
Proof:
We choose

Since  is open by assumption and
is open by assumption and  , for every
, for every  exists an
exists an  such that
such that

By theorem 6.15, we obtain in this case:

Further,

, which is why

Since

, we have even

By theorem 6.17 we conclude that

almost everywhere in  , and since
, and since

is continuous, even

really everywhere in  (see exercise 6). Therefore
(see exercise 6). Therefore  , and since
, and since  was arbitrary,
was arbitrary,  is open.
is open.
Also,

and  is continuous. Thus, as a one-point set is closed, lemma 3.13 says
is continuous. Thus, as a one-point set is closed, lemma 3.13 says  is closed in
is closed in  . Thus
. Thus  is simultaneously open and closed. By theorem 6.18, we obtain that either
is simultaneously open and closed. By theorem 6.18, we obtain that either  or
or  . And since by assumtion
. And since by assumtion  is not empty, we have
is not empty, we have  .
.
Proof: See exercise 7.
Proof:
Proof:
What we will do next is showing that every harmonic function  is in fact automatically contained in
is in fact automatically contained in  .
.
Proof:
Proof:
Proof:
Theorem 6.31:
Let  be a locally uniformly bounded sequence of harmonic functions. Then it has a locally uniformly convergent subsequence.
be a locally uniformly bounded sequence of harmonic functions. Then it has a locally uniformly convergent subsequence.
Proof:
The dirichlet problem for the Poisson equation is to find a solution for

If  is bounded, then we can know that if the problem
is bounded, then we can know that if the problem

has a solution  , then this solution is unique on
, then this solution is unique on  .
.
Proof:
Let  be another solution. If we define
be another solution. If we define  , then
, then  obviously solves the problem
obviously solves the problem

, since  for
for  and
and  for
for  .
.
Due to the above corollary from the minimum and maximum principle, we obtain that  is constantly zero not only on the boundary, but on the whole domain
is constantly zero not only on the boundary, but on the whole domain  . Therefore
. Therefore  on
on  . This is what we wanted to prove.
. This is what we wanted to prove.
Let  be a domain. Let
be a domain. Let  be the Green's kernel of Poisson's equation, which we have calculated above, i.e.
be the Green's kernel of Poisson's equation, which we have calculated above, i.e.

, where  denotes the surface area of
denotes the surface area of  .
.
Suppose there is a function  which satisfies
which satisfies

Then the Green's function of the first kind for  for
for  is defined as follows:
is defined as follows:

 is automatically a Green's function for
is automatically a Green's function for  . This is verified exactly the same way as veryfying that
. This is verified exactly the same way as veryfying that  is a Green's kernel. The only additional thing we need to know is that
is a Green's kernel. The only additional thing we need to know is that  does not play any role in the limit processes because it is bounded.
does not play any role in the limit processes because it is bounded.
A property of this function is that it satisfies

The second of these equations is clear from the definition, and the first follows recalling that we calculated above (where we calculated the Green's kernel), that  for
for  .
.
Let  be a domain, and let
be a domain, and let  be a solution to the Dirichlet problem
be a solution to the Dirichlet problem

. Then the following representation formula for  holds:
holds:

, where  is a Green's function of the first kind for
is a Green's function of the first kind for  .
.
Proof:
Let's define

. By the theorem of dominated convergence, we have that

Using multi-dimensional integration by parts, it can be obtained that:



When we proved the formula for the Green's kernel of Poisson's equation, we had already shown that
 and
and
The only additional thing which is needed to verify this is that  , which is why it stays bounded, while
, which is why it stays bounded, while  goes to infinity as
goes to infinity as  , which is why
, which is why  doesn't play a role in the limit process.
doesn't play a role in the limit process.
This proves the formula.
Harmonic functions on the ball: A special case of the Dirichlet problem
[edit | edit source]Let's choose

Then

is a Green's function of the first kind for  .
.
Proof: Since  and therefore
and therefore

Furthermore, we obtain:

, which is why  is a Green's function.
is a Green's function.
The property for the boundary comes from the following calculation:

, which is why  , since
, since  is radially symmetric.
is radially symmetric.
Let's consider the following problem:

Here  shall be continuous on
shall be continuous on  . Then the following holds: The unique solution
. Then the following holds: The unique solution  for this problem is given by:
for this problem is given by:

Proof: Uniqueness we have already proven; we have shown that for all Dirichlet problems for  on bounded domains (and the unit ball is of course bounded), the solutions are unique.
on bounded domains (and the unit ball is of course bounded), the solutions are unique.
Therefore, it only remains to show that the above function is a solution to the problem. To do so, we note first that

Let  be arbitrary. Since
be arbitrary. Since  is continuous in
is continuous in  , we have that on
, we have that on  it is bounded. Therefore, by the fundamental estimate, we know that the integral is bounded, since the sphere, the set over which is integrated, is a bounded set, and therefore the whole integral must be always below a certain constant. But this means, that we are allowed to differentiate under the integral sign on
it is bounded. Therefore, by the fundamental estimate, we know that the integral is bounded, since the sphere, the set over which is integrated, is a bounded set, and therefore the whole integral must be always below a certain constant. But this means, that we are allowed to differentiate under the integral sign on  , and since
, and since  was arbitrary, we can directly conclude that on
was arbitrary, we can directly conclude that on  ,
,

Furthermore, we have to show that  , i. e. that
, i. e. that  is continuous on the boundary.
is continuous on the boundary.
To do this, we notice first that

This follows due to the fact that if  , then
, then  solves the problem
solves the problem

and the application of the representation formula.
Furthermore, if  and
and  , we have due to the second triangle inequality:
, we have due to the second triangle inequality:

In addition, another application of the second triangle inequality gives:

Let then  be arbitrary, and let
be arbitrary, and let  . Then, due to the continuity of
. Then, due to the continuity of  , we are allowed to choose
, we are allowed to choose  such that
such that
 .
.
In the end, with the help of all the previous estimations we have made, we may unleash the last chain of inequalities which shows that the representation formula is true:



Since  implies
implies  , we might choose
, we might choose  close enough to
close enough to  such that
such that
 . Since
. Since  was arbitrary, this finishes the proof.
was arbitrary, this finishes the proof.
Let  be a domain. A function
be a domain. A function  is called a barrier with respect to
is called a barrier with respect to  if and only if the following properties are satisfied:
if and only if the following properties are satisfied:
 is continuous
is continuous is superharmonic on
is superharmonic on 


Let  be a domain. We say that it satisfies the exterior sphere condition, if and only if for all
be a domain. We say that it satisfies the exterior sphere condition, if and only if for all  there is a ball
there is a ball  such that
such that  for some
for some  and
and  .
.
Let  be a domain and
be a domain and  .
.
We call  subharmonic if and only if:
subharmonic if and only if:

We call  superharmonic if and only if:
superharmonic if and only if:

From this definition we can see that a function is harmonic if and only if it is subharmonic and superharmonic.
A superharmonic function  on
on  attains it's minimum on
attains it's minimum on  's border
's border  .
.
Proof: Almost the same as the proof of the minimum and maximum principle for harmonic functions. As an exercise, you might try to prove this minimum principle yourself.
Let  , and let
, and let  . If we define
. If we define

, then  .
.
Proof: For this proof, the very important thing to notice is that the formula for  inside
inside  is nothing but the solution formula for the Dirichlet problem on the ball. Therefore, we immediately obtain that
is nothing but the solution formula for the Dirichlet problem on the ball. Therefore, we immediately obtain that  is superharmonic, and furthermore, the values on
is superharmonic, and furthermore, the values on  don't change, which is why
don't change, which is why  . This was to show.
. This was to show.
Let  . Then we define the following set:
. Then we define the following set:

 is not empty and
is not empty and

Proof: The first part follows by choosing the constant function  , which is harmonic and therefore superharmonic. The second part follows from the minimum principle for superharmonic functions.
, which is harmonic and therefore superharmonic. The second part follows from the minimum principle for superharmonic functions.
Let  . If we now define
. If we now define  , then
, then  .
.
Proof: The condition on the border is satisfied, because

 is superharmonic because, if we (without loss of generality) assume that
is superharmonic because, if we (without loss of generality) assume that  , then it follows that
, then it follows that

, due to the monotony of the integral. This argument is valid for all  , and therefore
, and therefore  is superharmonic.
is superharmonic.
If  is bounded and
is bounded and  , then the function
, then the function

is harmonic.
Proof:
If  satisfies the exterior sphere condition, then for all
satisfies the exterior sphere condition, then for all  there is a barrier function.
there is a barrier function.
Let  be a bounded domain which satisfies the exterior sphere condition. Then the Dirichlet problem for the Poisson equation, which is, writing it again:
be a bounded domain which satisfies the exterior sphere condition. Then the Dirichlet problem for the Poisson equation, which is, writing it again:

has a solution  .
.
Proof:
Let's summarise the results of this section.
In the next chapter, we will have a look at the heat equation.
- Prove theorem 6.3 using theorem 6.2 (Hint: Choose
 in theorem 6.2).
in theorem 6.2).
- Prove that
 , where
, where  is the factorial of
is the factorial of  .
.
- Calculate
 . Have you seen the obtained function before?
. Have you seen the obtained function before?
- Prove that for
 , the function
, the function  as defined in theorem 6.11 is a Green's kernel for Poisson's equation (hint: use integration by parts twice).
as defined in theorem 6.11 is a Green's kernel for Poisson's equation (hint: use integration by parts twice).
- For all
 and
and  , calculate
, calculate  and
and  .
.
- Let
 be open and
be open and  be continuous. Prove that
be continuous. Prove that  almost everywhere in
almost everywhere in  implies
implies  everywhere in
everywhere in  .
.
- Prove theorem 6.20 by modelling your proof on the proof of theorem 6.19.
- For all dimensions
 , give an example for vectors
, give an example for vectors  such that neither
such that neither  nor
nor  .
.












































































































































































































































































































