OpenSCAD User Manual/Primitive Solids

cube

Creates a cube at the origin of the coordinate system. When center is true the cube will be centered on the origin, otherwise it is created in the first octant. The argument names are optional if the arguments are given in the same order as specified in the parameters

Parameters

size 

Decimal or 3 value array. If a single number is given, the result will be a cube with sides of that length. If a 3 value array is given, then the values will correspond to the lengths of the X, Y, and Z sides. Default value is 1.

center 

Boolean. This determines the positioning of the object. If true, object is centered at (0,0,0). Otherwise, the cube is placed in the positive quadrant with one corner at (0,0,0). Defaults to false

Usage examples:

cube(size = 1, center = false);
cube(size = [1,2,3], center = true);

sphere

Creates a sphere at the origin of the coordinate system. The argument name is optional.

Parameters

r 

Decimal. This is the radius of the sphere. The resolution of the sphere will be based on the size of the sphere and the $fa, $fs and $fn variables. For more information on these special variables look at: OpenSCAD_User_Manual/Other_Language_Features

$fa 

Angle in degrees

$fs 

Angle in mm

$fn 

Resolution

Usage Examples

sphere(r = 1);
sphere(r = 5);
sphere(r = 10);

// this will create a high resolution sphere with a 2mm radius
sphere(2, $fn=100); 

// will also create a 2mm high resolution sphere but this one 
// does not have as many small triangles on the poles of the sphere
sphere(2, $fa=5, $fs=0.1); 

cylinder

Creates a cylinder or cone at the origin of the coordinate system. A single radius (r) makes a cylinder, two different radi (r1, r2) make a cone.

Parameters

h 

Decimal. This is the height of the cylinder. Default value is 1.

r1 

Decimal. This is the radius of the cone on bottom end. Default value is 1.

r2 

Decimal. This is the radius of the cone on top end. Default value is 1.

r 

Decimal. The radius of both top and bottom ends of the cylinder. Use this parameter if you want plain cylinder. Default value is 1.

center 

boolean. If true will center the height of the cone/cylinder around the origin. Default is false, placing the base of the cylinder or r1 radius of cone at the origin.

$fa 

Angle in degrees

$fs 

Angle in mm

$fn 

Resolution

Usage Examples

cylinder(h = 10, r1 = 10, r2 = 20, center = false);
cylinder(h = 10, r1 = 20, r2 = 10, center = true);
cylinder(h = 10, r=20);
cylinder(h = 10, r=20, $fs=6);

polyhedron

Create a polyhedron with a list of points and a list of triangles. The point list is all the vertexes of the shape, the triangle list is how the points relates to the surfaces of the polyhedron.

Parameters

points 

vector of points or vertexes (each a 3 vector).

triangles 

vector of point triplets (each a 3 number vector). Each number is the 0-indexed point number from the point vector.

convexity

Integer. The convexity parameter specifies the maximum number of front sides (back sides) a ray intersecting the object might penetrate. This parameter is only needed for correctly displaying the object in OpenCSG preview mode and has no effect on the polyhedron rendering.

Syntax example

 polyhedron(points = [ [x, y, z], ... ], triangles = [ [p1, p2, p3..], ... ], convexity = N);

Triangle points ordering When looking at the face from the outside inwards, the points must be clockwise. You can rearrange the order of the points or the order they are referenced in each triangle triple. The order of triangles is immaterial. Note that if your polygons are not all oriented the same way OpenSCAD will either print an error or crash completely, so pay attention to the vertex ordering. Again, remember that the 'pN' components of the triangles vector are 0-indexed references to the elements of the points vector.

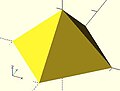
Example, a square base pyramid:

polyhedron(
  points=[ [10,10,0],[10,-10,0],[-10,-10,0],[-10,10,0], // the four points at base
           [0,0,10]  ],                                 // the apex point 
  triangles=[ [0,1,4],[1,2,4],[2,3,4],[3,0,4],          // each triangle side
              [1,0,3],[2,1,3] ]                         // two triangles for square base
 );

A simple polyhedron, square based pyramid

Ordering of triangle points An example of a more complex polyhedron, and showing how to fix polyhedrons with badly oriented polygons.

When you select 'Thrown together' from the view menu and compile the design (not compile and render!) you will see a preview with the mis-oriented polygons highlighted. Unfortunately this highlighting is not possible in the OpenCSG preview mode because it would interfere with the way the OpenCSG preview mode is implemented.)

Below you can see the code and the picture of such a problematic polyhedron, the bad polygons (triangles or compositions of triangles) are in pink.

// Bad polyhedron
polyhedron
    (points = [
               [0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60], 
               [10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
               ], 
     triangles = [
                  [0,2,3],   [0,1,2],  [0,4,5],  [0,5,1],   [5,4,2],  [2,4,3],
                  [6,8,9],  [6,7,8],  [6,10,11], [6,11,7], [10,8,11],
                  [10,9,8], [0,3,9],  [9,0,6], [10,6, 0],  [0,4,10],
                  [3,9,10], [3,10,4], [1,7,11],  [1,11,5], [1,7,8],  
                  [1,8,2],  [2,8,11], [2,11,5]
                  ]
     );

Polyhedron with badly oriented polygons

A correct polyhedron would be the following:

polyhedron
    (points = [
               [0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60], 
               [10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
               ], 
     triangles = [
                  [0,3,2],  [0,2,1],  [4,0,5],  [5,0,1],  [5,2,4],  [4,2,3],
                  [6,8,9],  [6,7,8],  [6,10,11],[6,11,7], [10,8,11],
                  [10,9,8], [3,0,9],  [9,0,6],  [10,6, 0],[0,4,10],
                  [3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,8,7],  
                  [2,8,1],  [8,2,11], [5,11,2]
                  ]
     );

Beginner's tip:

If you don't really understand "orientation", try to identify the mis-oriented pink triangles and then permute the references to the points vectors until you get it right. E.g. in the above example, the third triangle ([0,4,5]) was wrong and we fixed it as [4,0,5]. In addition, you may select "Show Edges" from the "View Menu", print a screen capture and number both the points and the triangles. In our example, the points are annotated in black and the triangles in blue. Turn the object around and make a second copy from the back if needed. This way you can keep track.

Clockwise Technique:

Orientation is determined by clockwise indexing. This means that if you're looking at the triangle (in this case [4,0,5]) from the outside you'll see that the path is clockwise around the center of the face. The winding order [4,0,5] is clockwise and therefore good. The winding order [0,4,5] is counter-clockwise and therefore bad. Likewise, any other clockwise order of [4,0,5] works: [5,4,0] & [0,5,4] are good too. If you use the clockwise technique, you'll always have your faces outside (outside of OpenSCAD, other programs do use counter-clockwise as the outside though).

Think of it as a Left Hand Rule:

If you hold the triangle and the fingers of your hand curls is the same order as the points, then your thumb points outwards.

Polyhedron with badly oriented polygons

Succinct description of a 'Polyhedron'

* Points define all of the points/vertices in the shape.
* Triangles is a list of triangles that connect up the points/vertices. 

Each point, in the point list, is defined with a 3-tuple x,y,z position specification. Points in the point list are automatically given an identifier starting at zero for use in the triangle list (0,1,2,3,... etc).

Each triangle, in the triangle list, is defined by selecting 3 of the points (using the point identifier) out of the point list.

e.g. triangles=[ [0,1,2] ] defines a triangle from the first point (points are zero referenced) to the second point and then to the third point.

When looking at any triangle from the outside, the triangle must list their 3 points in a clockwise order.