Mathematical Proof/Introduction to Set Theory
Objects known as sets are often used in mathematics, and there exists set theory which studies them. Although set theory can be discussed formally [1], it is not necessary for us to have such a formal discussion in this book, and we may not be interested in and understand the formal discussion in this stage.
Even if we do not discuss set theory formally, it is important for us to understand some basic concepts about sets, which will be covered in this chapter.
What is a set?
[edit | edit source]A set may be viewed as a collection of well-defined, distinct objects (the objects can also be sets). Because of the vagueness of the term "well-defined", we do not regard this as the definition of set. Instead, we regard set as a primitive notion (i.e., concepts not defined in terms of previously-defined concepts). Other examples of primitive notions in mathematics include point and line.
We have mentioned that a set is a collection of well-defined, distinct objects. Objects in a set are called elements of the set. We write to mean that the element belongs to the set . If does not belong to , we write .
Example.
- Consider the set of all even numbers . Elements of include (but are not limited to) -2, 0, and 4, i.e., .
- The elements of the English alphabet (a set) are English letters.
Ways of describing a set
[edit | edit source]There are multiple ways to describe a set precisely (in the sense that element(s) belonging to the set is (are) known precisely).
If a set consists of a small number of elements, then the listing method may be quite efficient. In the listing method, elements of a set are listed within a pair of braces ({}). In particular, just changing the listing order of elements does not change the set represented. For example, and are both representing the same set whose elements are 1 and 2. If the elements listed in the pair of braces are the same, the notations created by the listing method with different listing orders refer to the same set. Also, repeatedly listing a specific element in a set does not change the set represented. For example, and are both representing the same set whose elements are 1 and 2. In particular, if a set contains no elements, it can be denoted by based on the listing method or . This kind of set is called an empty set.
Another way to describe a set is using words. For example, consider the set of prime numbers less than 10. If we use the listing method instead, the set is represented by .
The third way to describe a set is advantageous when a set contains many elements. This method is called set-builder notation. There are three parts within a pair of braces in this notation. They are illustrated below with descriptions:
As one may expect, two sets are equal if and only if they contain the same elements. Equivalently, two sets and are equal if and only if each element of is also an element of and each element of is also an element of . This can be regarded as an axiom [2] or a definition. If two sets and are equal, we write . If not, we write .
In this book, when we are solving an equation, we are only considering its real solution(s) unless stated otherwise.
Example.
- .
- .
- .
Set cardinality
[edit | edit source]If a set contains finite number of elements, it is called a finite set, and it is called an infinite set otherwise. If a set is finite, then its cardinality is its number of elements. For infinite sets, it is harder and more complicated to define their cardinalities, and so we will do this in the later chapter about set cardinalities. For each set , its cardinality is denoted by .
Example.
- Let . Then, .
- Let . Then, (not 3 since the element is listed repeatedly).
- Let . Then, since there is no solution for (for real number ), and thus is an empty set.
- Let . Solving , we have . Hence, and thus [3].
There are some special infinite sets for which notations are given, as follows:
- is the set of all natural numbers (0 is not regarded as a natural number in this book).
- is the set of all integers.
- is the set of all rational numbers.
- (nonstandard notation) is the set of all irrational numbers.
- is the set of all real numbers.
- is the set of all complex numbers.
In particular, we can use set-builder notation to express , as follows: .
Example.

Exercise. Use set-builder notation to express without using "" in the expression.
We can express like this: ().
Subsets
[edit | edit source]Definition. (Subset) A set is a subset of a set (denoted by ) if each element of is also an element of .
Remark.
- If is not a subset of , we denote it as .
- Recall that two sets and if and only if each element of belongs to and each element of belongs to . Using the notion of subsets, we can write if and only if and .
Example.
- .
- (e.g. but )
- (e.g. but )
- For each set , , i.e. each set is a subset of itself.
- This is because each element of set is an element of .
- For each set , .
- If we want to prove this directly, there are some difficulties since does not contain any element. So, what is meant by "each element of "?
- Under this situation, it may be better to prove by contradiction (a proof technique covered in the later chapter about methods of proof). First, we suppose on the contrary that . By the negation of the definition, there is at least one element of that is not an element of , which is false. This yields a contradiction, and thus the hypothesis is false (explanation will be provided later), i.e. is false.
Definition. (Proper subset) A set is a proper subset of a set (denoted by ) if is a subset of and .
Remark.
- Similarly, if is not a proper subset of , we write .
Example.
- For each nonempty set , since (shown previously) and if is a nonempty set.
- .
- .
- and .
We call some commonly encountered subsets of intervals. For each real number such that ,
- (open intervals)
- (half-open (or half-closed) intervals)
- (half-open (or half-closed) intervals)
- (closed intervals)
There are also some infinite intervals:
Note: is a shorthand of ( is a set).
Example.
- .
- .
- since the element "1" of the set on LHS does not belong to the set on RHS.
- .
Example.
- The set of (real) solutions of is .
- The set of (real) solutions of is . (Note: we cannot express this set as since it is required that for an interval .)
- The set of (real) solutions of is .
Universal set and Venn diagram
[edit | edit source]Definition. (Universal set) A universal set, denoted by , is a set containing all elements considered in a certain investigation.
Example.
- If we are studying real numbers, the universal set is .
Definition. (Complement) The complement of a set that is a subset of the universal set , denoted by , is the set .
Example.
- Let and . Then, . (Note: also.)
- For each universal set , (since each element of does not belong to [4]) and (since there are no elements of that does not belong to ).
- Let and . Then, since each element of does not belong to .
A Venn diagram is a diagram showing all possible logical relationships between a finite number of sets. The universal set is usually represented by a region enclosed by a rectangle, while the sets are usually represents by regions enclosed by circles. The following is a Venn diagram.

In this diagram, if the white region represents set and the region enclosed by the rectangle represents the universal set, then the red region is the set .
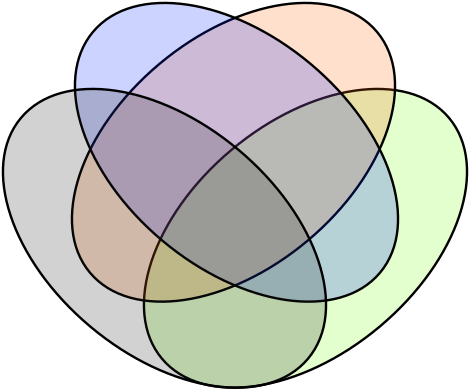
However, the following is not a Venn diagram.
This is because there are not regions in which only the yellow and blue region intersect, and only the red and green region intersect, respectively. So, not all logical relationships between the sets are shown.
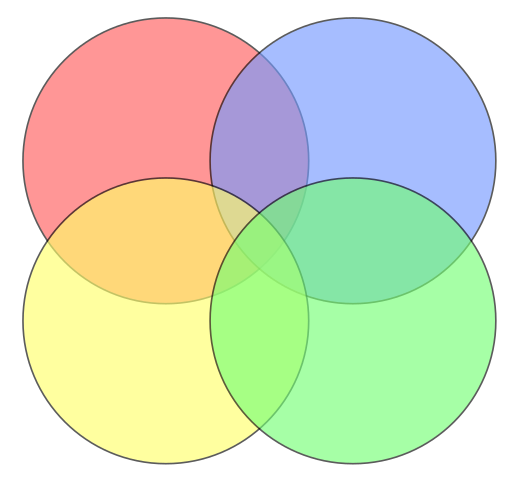
To show all logical relationships between four sets, the following Venn diagram can be used.
Set operations
[edit | edit source]Similar to the arithmetic operations for real numbers which combine two numbers into one, the set operations combine two sets into one.
Union of sets
[edit | edit source]Definition. (Union of sets)
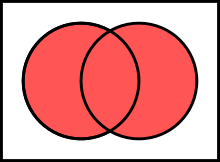
The union of a set and a set , denoted by , is the set .
Remark.
- The "or" here is inclusive, i.e. if an element belongs to both and , it also belongs to .
Example.
- .
- .
- .
- .
Proposition. Let and be sets. Then,
- (commutative law)
- (associative law)
- and
Proof. (Formal) proof will be discussed later. For now, you may verify these results using Venn diagram.
Remark.
- Because of the associative law, we can write union of three (or more) sets without brackets. We will have similar results for intersection of sets, and so we can also write intersection of three (or more) sets without brackets.
Intersection of sets
[edit | edit source]Definition. (Intersection of sets)

The intersection of a set and a set , denoted by , is the set .
Remark.
- If , we say that and are disjoint.
Proposition. Let and be sets. Then,
- (commutative law)
- (associative law)
- and
Proof. (Formal) proof will be discussed later. For now, you may verify these results using Venn diagram.
Proposition. (Distributive laws) Let and be sets. Then,
- (the "" is "distributed" to and respectively)
Relative complement
[edit | edit source]Definition. (Relative complement)

The relative complement of a set in a set , denoted by , is the set .
Remark.
- if is the universal set. So, the complement of a set is also the relative complement of in .
- The notation is read "B with A taken away".
- We can see from the definition that
Example.
- .
- .
- .
- .
- .
Proposition. Let and be sets. Then,
- .
- .
- .
- if and only if .
- .
- .
Proof. (Formal) proof will be discussed later. For now, you may verify these results using Venn diagram.
Theorem. (De Morgan's Laws) Let and be sets. Then,
Proof. (Formal) proof will be discussed later. For now, you may verify these results using Venn diagram.
Symmetric difference
[edit | edit source]Definition. (Symmetric difference)
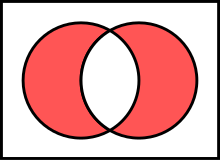
The symmetric difference of sets and , denoted by , is the set .
Example.
- .
Proposition. Let and be sets. Then,
- (associative law)
- (commutative law)
Power set
[edit | edit source]Definition. (Power set) The power set of a set , denoted by , is the set of all subsets of . In set-builder notation, .
Remark.
- Since for each set , is an element of each power set.
- Also, since for each set , is an element of the power set .
Example.
- . Its cardinality is 1.
- If , then . Its cardinality is 2.
- If , then . Its cardinality is 4.
- . Its cardinality is 8.
Theorem. (Cardinality of power set of a finite set) Let be a finite set with cardinality . Then, .
Proof. Assume is a finite set with cardinality . Since each element of the power set is a subset of , it suffices to prove that there are subsets of . In the following, we consider subsets of with different number of elements separately, and count the number of subsets of each of the different types using combinatorics.
- For the subset with zero element, it is the empty set, and thus there is only one such subset.
- For the subsets with one element, there are subsets.
- For the subsets with two elements, there are subsets.
- ...
- For the subsets with elements, there are subsets.
- For the subset with elements, it is the set , and thus there is only one such subset.
So, the total number of subsets of is by binomial theorem.
Remark.
- The proof method employed here is called direct proof, which is probably the most "natural" method, and most commonly used. We will discuss methods of proof in a later chapter.
- There are alternative ways to prove this theorem.

Exercise. In each of the following questions, choose the power set of the set given in the question.
It is given that . In each of the following questions, choose the cardinality of the set given in the question.
Cartesian product
[edit | edit source]Definition. (Cartesian product) The Cartesian product of sets and , denoted by , is .
Remark.
- is the ordered pair (i.e. a pair of things for which order is important).
- The ordered pair is used to specify points on the plane, and the ordered pair is called coordinates.
- In particular, we have if .
- (notation) We use to denote for each set .
- We can observe that .
Example. Let and . Then,
- .
- .
Remark.
- We can see from the above example that the Cartesian product is not commutative, i.e. it is not necessary for .
Similarly, we can define the Cartesian product of three or more sets.
Definition. (Cartesian product of three or more sets) Let be an integer greater than 2. The Cartesian product of sets is .
Remark.
- (notation) We use to denote , where .
- ↑ There are various types of axiomatic set theory, in which Zermelo-Fraenkel set theory is the most well-known one.
- ↑ . Indeed, this is the axiom of extension in the Zermelo-Fraenkel set theory.
- ↑ For sets with exactly one element, they are called singleton. In this case, is a singleton.
- ↑ There are no elements belonging to .
- ↑ We need not to write brackets for LHS because of the associative law.









































































![{\displaystyle (a,b]{\overset {\text{ def }}{=}}\{x\in \mathbb {R} :a<x\leq b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f92a9e15e26f90bfe2e97c3a8e5d687b45465be)

![{\displaystyle [a,b]{\overset {\text{ def }}{=}}\{x\in \mathbb {R} :a\leq x\leq b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9731bc8ce6e53044fa2f72456c5935550713e5b5)

![{\displaystyle (-\infty ,a]{\overset {\text{ def }}{=}}\{x\in \mathbb {R} :x\leq a\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aa90551091f0e63100137abfaf6413b84f2e70d)





![{\displaystyle (0,1)\subseteq [0,1)\subseteq [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f5ebbbaa576a62df2a3c8cf0bdc0a8ea20583bc)

![{\displaystyle (0,1]\not \subseteq [0,1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/946799c9a98a0d16c8d3a8c0809c97e8eb7777c5)


![{\displaystyle [-3,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a869f6f7ff84a95f888c6b8705e2465ba21960e)


![{\displaystyle [0,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e543f601fac1a6510c6fd606aee4cae29fc1a79)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)










































































































