Materials in Electronics/Wave-Particle Duality/The Two-Slit Experiment/Electrons
According to classical physics, electrons should behave like particles - they travel in straight lines and do not curve in flight unless acted on by an external agent, like a magnetic field. In this model, if we fire a beam of electrons through a double slit onto a detector, we should get two bands of "hits", much as you would get if you fired a machine gun at the side of a house with two windows - you would get two areas of bullet-marked wall inside, and the rest would be intact.
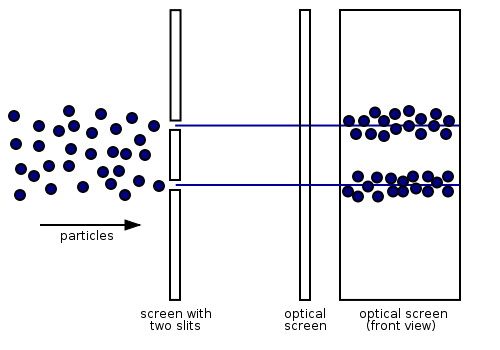
This was the behaviour noted for years. However, if the slits are made small enough and close enough together, we actually observe the following:

This means that the electrons are diffracting through the slits and interfering with each other just like waves. This means that the electrons have wave-particle duality, just like photons. In this case, they must have properties like wavelength and frequency. We can deduce the properties from the behaviour of the electrons as they pass through our diffraction grating.
Recall the property relating wavelength to diffraction fringe spacing that we found earlier:
where
- s is the fringe spacing
- λ is the wavelength
- L is the distance from slits to screen
- d is the grating spacing
If we can get electrons to diffract through a known grating, we can obtain a wavelength for the electron. This could also be derived theoretically, but it requires relativity, and is certainly a non-trival exercise. Practically, it turns out that electrons have an extremely short wavelength, so we cannot make gratings fine enough to diffract them significantly using traditional methods. However, we can use crystals as they are essentially extremely regular gratings with a spacing on the order of nanometres.
If we use an electron gun to produce our electrons, and fire these electrons though a crystal with a known atomic structure, we can work out the wavelength of the electron experimentally. This leads to a description of the electron as a wave. This is expanded on here.
