Linear Algebra/Representing Linear Maps with Matrices/Solutions

Solutions

This exercise is recommended for all readers.

Problem 1

Multiply the matrix

$\begin{pmatrix} 1 &3 &1 \\ 0 &-1 &2 \\ 1 &1 &0 \end{pmatrix}$

by each vector (or state "not defined").

1. $\begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}$
2. $\begin{pmatrix} -2 \\ -2 \end{pmatrix}$
3. $\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$

Answer

1. $\begin{pmatrix} 1\cdot 2+3\cdot 1+1\cdot 0 \\ 0\cdot 2+(-1)\cdot 1+2\cdot 0 \\ 1\cdot 2+1\cdot 1+0\cdot 0 \end{pmatrix} =\begin{pmatrix} 5 \\ -1 \\ 3 \end{pmatrix}$
2. Not defined.
3. $\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$

Problem 2

Perform, if possible, each matrix-vector multiplication.

1. $\begin{pmatrix} 2 &1 \\ 3 &-1/2 \end{pmatrix} \begin{pmatrix} 4 \\ 2 \end{pmatrix}$
2. $\begin{pmatrix} 1 &1 &0 \\ -2 &1 &0 \end{pmatrix} \begin{pmatrix} 1 \\ 3 \\ 1 \end{pmatrix}$
3. $\begin{pmatrix} 1 &1 \\ -2 &1 \end{pmatrix} \begin{pmatrix} 1 \\ 3 \\ 1 \end{pmatrix}$

Answer

1. $\begin{pmatrix} 2\cdot 4 +1\cdot 2 \\ 3\cdot 4-(1/2)\cdot 2 \end{pmatrix} =\begin{pmatrix} 10 \\ 11 \end{pmatrix}$
2. $\begin{pmatrix} 4 \\ 1 \end{pmatrix}$
3. Not defined.

This exercise is recommended for all readers.

Problem 3

Solve this matrix equation.

$\begin{pmatrix} 2 &1 &1 \\ 0 &1 &3 \\ 1 &-1 &2 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} =\begin{pmatrix} 8 \\ 4 \\ 4 \end{pmatrix}$

Answer

Matrix-vector multiplication gives rise to a linear system.

$\begin{array}{*{3}{rc}r} 2x &+ &y &+ &z &= &8 \\ & &y &+ &3z &= &4 \\ x &- &y &+ &2z &= &4 \end{array}$

Gaussian reduction shows that $z=1$, $y=1$, and $x=3$.

This exercise is recommended for all readers.

Problem 4

For a homomorphism from $\mathcal{P}_2$ to $\mathcal{P}_3$ that sends

$1\mapsto 1+x, \quad x\mapsto 1+2x, \quad\text{and}\quad x^2\mapsto x-x^3$

where does $1-3x+2x^2$ go?

Answer

Here are two ways to get the answer.

First, obviously $1-3x+2x^2=1\cdot 1-3\cdot x+2\cdot x^2$, and so we can apply the general property of preservation of combinations to get $h(1-3x+2x^2) =h(1\cdot 1-3\cdot x+2\cdot x^2) =1\cdot h(1)-3\cdot h(x)+2\cdot h(x^2) =1\cdot (1+x)-3\cdot (1+2x)+2\cdot (x-x^3) =-2-3x-2x^3$.

The other way uses the computation scheme developed in this subsection. Because we know where these elements of the space go, we consider this basis $B=\langle 1,x,x^2 \rangle$ for the domain. Arbitrarily, we can take $D=\langle 1,x,x^2,x^3 \rangle$ as a basis for the codomain. With those choices, we have that

${\rm Rep}_{B,D}(h) =\begin{pmatrix} 1 &1 &0 \\ 1 &2 &1 \\ 0 &0 &0 \\ 0 &0 &-1 \end{pmatrix}_{B,D}$

and, as

${\rm Rep}_{B}(1-3x+2x^2)=\begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix}_B$

the matrix-vector multiplication calculation gives this.

${\rm Rep}_{D}(h(1-3x+2x^2))= \begin{pmatrix} 1 &1 &0 \\ 1 &2 &1 \\ 0 &0 &0 \\ 0 &0 &-1 \end{pmatrix}_{B,D} \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix}_B =\begin{pmatrix} -2 \\ -3 \\ 0 \\ -2 \end{pmatrix}_D$

Thus, $h(1-3x+2x^2) =-2\cdot 1-3\cdot x+0\cdot x^2-2\cdot x^3 =-2-3x-2x^3$, as above.

This exercise is recommended for all readers.

Problem 5

Assume that $h:\mathbb{R}^2\to \mathbb{R}^3$ is determined by this action.

$\begin{pmatrix} 1 \\ 0 \end{pmatrix}\mapsto\begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix} \qquad \begin{pmatrix} 0 \\ 1 \end{pmatrix}\mapsto\begin{pmatrix} 0 \\ 1 \\ -1 \end{pmatrix}$

Using the standard bases, find

1. the matrix representing this map;
2. a general formula for $h(\vec{v})$.

Answer

Again, as recalled in the subsection, with respect to $\mathcal{E}_i$, a column vector represents itself.

1. To represent $h$ with respect to $\mathcal{E}_2,\mathcal{E}_3$ we take the images of the basis vectors from the domain, and represent them with respect to the basis for the codomain.

   ${\rm Rep}_{\mathcal{E}_3}(\,h(\vec{e}_1)\,) ={\rm Rep}_{\mathcal{E}_3}(\begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix}) =\begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix} \qquad {\rm Rep}_{\mathcal{E}_3}(\,h(\vec{e}_2)\,) ={\rm Rep}_{\mathcal{E}_3}(\begin{pmatrix} 0 \\ 1 \\ -1 \end{pmatrix}) =\begin{pmatrix} 0 \\ 1 \\ -1 \end{pmatrix}$

   These are adjoined to make the matrix.

   ${\rm Rep}_{\mathcal{E}_2,\mathcal{E}_3}(h)= \begin{pmatrix} 2 &0 \\ 2 &1 \\ 0 &-1 \end{pmatrix}$

2. For any $\vec{v}$ in the domain $\mathbb{R}^2$,

   ${\rm Rep}_{\mathcal{E}_2}(\vec{v}) ={\rm Rep}_{\mathcal{E}_2}(\begin{pmatrix} v_1 \\ v_2 \end{pmatrix}) =\begin{pmatrix} v_1 \\ v_2 \end{pmatrix}$

   and so

   ${\rm Rep}_{\mathcal{E}_3}(\,h(\vec{v})\,) =\begin{pmatrix} 2 &0 \\ 2 &1 \\ 0 &-1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} =\begin{pmatrix} 2v_1 \\ 2v_1+v_2 \\ -v_2 \end{pmatrix}$

   is the desired representation.

This exercise is recommended for all readers.

Problem 6

Let $d/dx:\mathcal{P}_3\to \mathcal{P}_3$ be the derivative transformation.

1. Represent $d/dx$ with respect to $B,B$ where $B=\langle 1,x,x^2,x^3 \rangle$.
2. Represent $d/dx$ with respect to $B,D$ where $D=\langle 1,2x,3x^2,4x^3 \rangle$.

Answer

1. We must first find the image of each vector from the domain's basis, and then represent that image with respect to the codomain's basis.

   ${\rm Rep}_{B}(\frac{d\,1}{dx})=\begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} \quad {\rm Rep}_{B}(\frac{d\,x}{dx})=\begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \quad {\rm Rep}_{B}(\frac{d\,x^2}{dx})=\begin{pmatrix} 0 \\ 2 \\ 0 \\ 0 \end{pmatrix} \quad {\rm Rep}_{B}(\frac{d\,x^3}{dx})=\begin{pmatrix} 0 \\ 0 \\ 3 \\ 0 \end{pmatrix}$

   Those representations are then adjoined to make the matrix representing the map.

   ${\rm Rep}_{B,B}(\frac{d}{dx})= \begin{pmatrix} 0 &1 &0 &0 \\ 0 &0 &2 &0 \\ 0 &0 &0 &3 \\ 0 &0 &0 &0 \end{pmatrix}$

2. Proceeding as in the prior item, we represent the images of the domain's basis vectors

   ${\rm Rep}_{B}(\frac{d\,1}{dx})=\begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} \quad {\rm Rep}_{B}(\frac{d\,x}{dx})=\begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \quad {\rm Rep}_{B}(\frac{d\,x^2}{dx})=\begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \quad {\rm Rep}_{B}(\frac{d\,x^3}{dx})=\begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}$

   and adjoin to make the matrix.

   ${\rm Rep}_{B,D}(\frac{d}{dx})= \begin{pmatrix} 0 &1 &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1 \\ 0 &0 &0 &0 \end{pmatrix}$

This exercise is recommended for all readers.

Problem 7

Represent each linear map with respect to each pair of bases.

1. $d/dx:\mathcal{P}_n\to \mathcal{P}_n$ with respect to $B,B$ where $B=\langle 1,x,\dots,x^n \rangle$, given by

   $a_0+a_1x+a_2x^2+\dots+a_nx^n \mapsto a_1+2a_2x+\dots+na_nx^{n-1}$

2. $\int:\mathcal{P}_n\to \mathcal{P}_{n+1}$ with respect to $B_n,B_{n+1}$ where $B_i=\langle 1,x,\dots,x^i \rangle$, given by

   $a_0+a_1x+a_2x^2+\dots+a_nx^n \mapsto a_0x+\frac{a_1}{2}x^2+\dots+\frac{a_n}{n+1}x^{n+1}$

3. $\int^1_0:\mathcal{P}_n\to \mathbb{R}$ with respect to $B,\mathcal{E}_1$ where $B=\langle 1,x,\dots,x^n \rangle$ and $\mathcal{E}_1=\langle 1 \rangle$, given by

   $a_0+a_1x+a_2x^2+\dots+a_nx^n \mapsto a_0+\frac{a_1}{2}+\dots+\frac{a_n}{n+1}$

4. $\text{eval}_3:\mathcal{P}_n\to \mathbb{R}$ with respect to $B,\mathcal{E}_1$ where $B=\langle 1,x,\dots,x^n \rangle$ and $\mathcal{E}_1=\langle 1 \rangle$, given by

   $a_0+a_1x+a_2x^2+\dots+a_nx^n \mapsto a_0+a_1\cdot 3+a_2\cdot 3^2+\dots+a_n\cdot 3^n$

5. $\text{slide}_{-1}:\mathcal{P}_n\to \mathcal{P}_n$ with respect to $B,B$ where $B=\langle 1,x,\ldots,x^n \rangle$, given by

   $a_0+a_1x+a_2x^2+\dots+a_nx^n \mapsto a_0+a_1\cdot (x+1)+\dots+a_n\cdot (x+1)^n$

Answer

For each, we must find the image of each of the domain's basis vectors, represent each image with respect to the codomain's basis, and then adjoin those representations to get the matrix.

1. The basis vectors from the domain have these images

   $1\mapsto 0 \quad x\mapsto 1 \quad x^2\mapsto 2x \quad \ldots$

   and these images are represented with respect to the codomain's basis in this way.

   ${\rm Rep}_{B}(0)=\begin{pmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ \ \\ \ \end{pmatrix} \quad {\rm Rep}_{B}(1)=\begin{pmatrix} 1 \\ 0 \\ 0 \\ \vdots \\ \ \\ \ \end{pmatrix} \quad {\rm Rep}_{B}(2x)=\begin{pmatrix} 0 \\ 2 \\ 0 \\ \vdots \\ \ \\ \ \end{pmatrix} \quad\ldots\quad {\rm Rep}_{B}(nx^{n-1})=\begin{pmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ n \\ 0 \end{pmatrix}$

   The matrix

   ${\rm Rep}_{B,B}(\frac{d}{dx}) =\begin{pmatrix} 0 &1 &0 &\ldots &0 \\ 0 &0 &2 &\ldots &0 \\ &\vdots \\ 0 &0 &0 &\ldots &n \\ 0 &0 &0 &\ldots &0 \end{pmatrix}$

   has $n+1$ rows and columns.
2. Once the images under this map of the domain's basis vectors are determined

   $1\mapsto x \quad x\mapsto x^2/2 \quad x^2\mapsto x^3/3 \quad \ldots$

   then they can be represented with respect to the codomain's basis

   ${\rm Rep}_{B_{n+1}}(x)=\begin{pmatrix} 0 \\ 1 \\ 0 \\ \vdots \\ \ \end{pmatrix} \quad {\rm Rep}_{B_{n+1}}(x^2/2)=\begin{pmatrix} 0 \\ 0 \\ 1/2 \\ \vdots \\ \ \end{pmatrix} \quad\ldots\quad {\rm Rep}_{B_{n+1}}(x^{n+1}/(n+1)) =\begin{pmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 1/(n+1) \end{pmatrix}$

   and put together to make the matrix.

   ${\rm Rep}_{B_{n},B_{n+1}}(\int) =\begin{pmatrix} 0 &0 &\ldots &0 &0 \\ 1 &0 &\ldots &0 &0 \\ 0 &1/2&\ldots &0 &0 \\ &\vdots \\ 0 &0 &\ldots &0 &1/(n+1) \end{pmatrix}$

3. The images of the basis vectors of the domain are

   $1\mapsto 1 \quad x\mapsto 1/2 \quad x^2\mapsto 1/3 \quad \ldots$

   and they are represented with respect to the codomain's basis as

   ${\rm Rep}_{\mathcal{E}_1}(1)=1 \quad {\rm Rep}_{\mathcal{E}_1}(1/2)=1/2 \quad \ldots$

   so the matrix is

   ${\rm Rep}_{B,\mathcal{E}_1}(\int) =\begin{pmatrix} 1 &1/2 &\cdots &1/n &1/(n+1) \end{pmatrix}$

   (this is an $1 \! \times \! (n+1)$ matrix).
4. Here, the images of the domain's basis vectors are

   $1\mapsto 1 \quad x\mapsto 3 \quad x^2\mapsto 9 \quad \ldots$

   and they are represented in the codomain as

   ${\rm Rep}_{\mathcal{E}_1}(1)=1 \quad{\rm Rep}_{\mathcal{E}_1}(3)=3 \quad{\rm Rep}_{\mathcal{E}_1}(9)=9 \quad \ldots$

   and so the matrix is this.

   ${\rm Rep}_{B,\mathcal{E}_1}(\int_0^1) =\begin{pmatrix} 1 &3 &9 &\cdots &3^n \end{pmatrix}$

5. The images of the basis vectors from the domain are

   $1\mapsto 1 \quad x\mapsto x+1=1+x \quad x^2\mapsto (x+1)^2=1+2x+x^2 \quad x^3\mapsto (x+1)^3=1+3x+3x^2+x^3 \quad \ldots$

   which are represented as

   ${\rm Rep}_{B}(1)=\begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \\ \vdots \\ 0 \end{pmatrix} \quad {\rm Rep}_{B}(1+x)=\begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{pmatrix} \quad {\rm Rep}_{B}(1+2x+x^2)=\begin{pmatrix} 1 \\ 2 \\ 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} \quad\ldots$

   The resulting matrix

   ${\rm Rep}_{B,B}(\int) =\begin{pmatrix} 1 &1 &1 &1 &\ldots &1 \\ 0 &1 &2 &3 &\ldots &\binom{n}{2} \\ 0 &0 &1 &3 &\ldots &\binom{n}{3} \\ &\vdots \\ 0 &0 &0 & &\ldots &1 \end{pmatrix}$

   is Pascal's triangle (recall that $\binom{n}{r}$ is the number of ways to choose $r$ things, without order and without repetition, from a set of size $n$).

Problem 8

Represent the identity map on any nontrivial space with respect to $B,B$, where $B$ is any basis.

Answer

Where the space is $n$-dimensional,

${\rm Rep}_{B,B}(\text{id})= \begin{pmatrix} 1 &0 \ldots &0 \\ 0 &1 \ldots &0 \\ &\vdots \\ 0 &0 \ldots &1 \end{pmatrix}_{B,B}$

is the $n \! \times \! n$ identity matrix.

Problem 9

Represent, with respect to the natural basis, the transpose transformation on the space $\mathcal{M}_{2 \! \times \! 2}$ of $2 \! \times \! 2$ matrices.

Answer

Taking this as the natural basis

$B=\langle \vec{\beta}_1,\vec{\beta}_2,\vec{\beta}_3,\vec{\beta}_4 \rangle =\langle \begin{pmatrix} 1 &0 \\ 0 &0 \end{pmatrix}, \begin{pmatrix} 0 &1 \\ 0 &0 \end{pmatrix}, \begin{pmatrix} 0 &0 \\ 1 &0 \end{pmatrix}, \begin{pmatrix} 0 &0 \\ 0 &1 \end{pmatrix} \rangle$

the transpose map acts in this way

$\vec{\beta}_1\mapsto\vec{\beta}_1 \quad \vec{\beta}_2\mapsto\vec{\beta}_3 \quad \vec{\beta}_3\mapsto\vec{\beta}_2 \quad \vec{\beta}_4\mapsto\vec{\beta}_4$

so that representing the images with respect to the codomain's basis and adjoining those column vectors together gives this.

${\rm Rep}_{B,B}(\text{trans})= \begin{pmatrix} 1 &0 &0 &0 \\ 0 &0 &1 &0 \\ 0 &1 &0 &0 \\ 0 &0 &0 &1 \end{pmatrix}_{B,B}$

Problem 10

Assume that $B=\langle \vec{\beta}_1,\vec{\beta}_2,\vec{\beta}_3,\vec{\beta}_4 \rangle$ is a basis for a vector space. Represent with respect to $B,B$ the transformation that is determined by each.

1. $\vec{\beta}_1\mapsto\vec{\beta}_2$, $\vec{\beta}_2\mapsto\vec{\beta}_3$, $\vec{\beta}_3\mapsto\vec{\beta}_4$, $\vec{\beta}_4\mapsto\vec{0}$
2. $\vec{\beta}_1\mapsto\vec{\beta}_2$, $\vec{\beta}_2\mapsto\vec{0}$, $\vec{\beta}_3\mapsto\vec{\beta}_4$, $\vec{\beta}_4\mapsto\vec{0}$
3. $\vec{\beta}_1\mapsto\vec{\beta}_2$, $\vec{\beta}_2\mapsto\vec{\beta}_3$, $\vec{\beta}_3\mapsto\vec{0}$, $\vec{\beta}_4\mapsto\vec{0}$

Answer

1. With respect to the basis of the codomain, the images of the members of the basis of the domain are represented as

   ${\rm Rep}_{B}(\vec{\beta}_2)=\begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \quad {\rm Rep}_{B}(\vec{\beta}_3)=\begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} \quad {\rm Rep}_{B}(\vec{\beta}_4)=\begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \quad {\rm Rep}_{B}(\vec{0})=\begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix}$

   and consequently, the matrix representing the transformation is this.

   $\begin{pmatrix} 0 &0 &0 &0 \\ 1 &0 &0 &0 \\ 0 &1 &0 &0 \\ 0 &0 &1 &0 \end{pmatrix}$

2. $\begin{pmatrix} 0 &0 &0 &0 \\ 1 &0 &0 &0 \\ 0 &0 &0 &0 \\ 0 &0 &1 &0 \end{pmatrix}$
3. $\begin{pmatrix} 0 &0 &0 &0 \\ 1 &0 &0 &0 \\ 0 &1 &0 &0 \\ 0 &0 &0 &0 \end{pmatrix}$

Problem 11

Example 1.8 shows how to represent the rotation transformation of the plane with respect to the standard basis. Express these other transformations also with respect to the standard basis.

1. the dilation map $d_s$, which multiplies all vectors by the same scalar $s$
2. the reflection map $f_\ell$, which reflects all all vectors across a line $\ell$ through the origin

Answer

1. The picture of $d_s:\mathbb{R}^2\to \mathbb{R}^2$ is this.

   

   This map's effect on the vectors in the standard basis for the domain is

   $\begin{pmatrix} 1 \\ 0 \end{pmatrix}\stackrel{d_s}{\longmapsto}\begin{pmatrix} s \\ 0 \end{pmatrix} \qquad \begin{pmatrix} 0 \\ 1 \end{pmatrix}\stackrel{d_s}{\longmapsto}\begin{pmatrix} 0 \\ s \end{pmatrix}$

   and those images are represented with respect to the codomain's basis (again, the standard basis) by themselves.

   ${\rm Rep}_{\mathcal{E}_2}(\begin{pmatrix} s \\ 0 \end{pmatrix})=\begin{pmatrix} s \\ 0 \end{pmatrix} \qquad {\rm Rep}_{\mathcal{E}_2}(\begin{pmatrix} 0 \\ s \end{pmatrix})=\begin{pmatrix} 0 \\ s \end{pmatrix}$

   Thus the representation of the dilation map is this.

   ${\rm Rep}_{\mathcal{E}_2,\mathcal{E}_2}(d_s) =\begin{pmatrix} s &0 \\ 0 &s \end{pmatrix}$

2. The picture of $f_\ell:\mathbb{R}^2\to \mathbb{R}^2$ is this.

   

   Some calculation (see Problem I.1.20) shows that when the line has slope $k$

   $\begin{pmatrix} 1 \\ 0 \end{pmatrix} \stackrel{f_\ell}{\longmapsto}\begin{pmatrix} (1-k^2)/(1+k^2) \\ 2k/(1+k^2) \end{pmatrix} \qquad \begin{pmatrix} 0 \\ 1 \end{pmatrix} \stackrel{f_\ell}{\longmapsto}\begin{pmatrix} 2k/(1+k^2) \\ -(1-k^2)/(1+k^2) \end{pmatrix}$

   (the case of a line with undefined slope is separate but easy) and so the matrix representing reflection is this.

   ${\rm Rep}_{\mathcal{E}_2,\mathcal{E}_2}(f_\ell) =\frac{1}{1+k^2}\cdot\begin{pmatrix} 1-k^2 &2k \\ 2k &-(1-k^2) \end{pmatrix}$

This exercise is recommended for all readers.

Problem 12

Consider a linear transformation of $\mathbb{R}^2$ determined by these two.

$\begin{pmatrix} 1 \\ 1 \end{pmatrix}\mapsto\begin{pmatrix} 2 \\ 0 \end{pmatrix} \qquad \begin{pmatrix} 1 \\ 0 \end{pmatrix}\mapsto\begin{pmatrix} -1 \\ 0 \end{pmatrix}$

1. Represent this transformation with respect to the standard bases.
2. Where does the transformation send this vector?

   $\begin{pmatrix} 0 \\ 5 \end{pmatrix}$

3. Represent this transformation with respect to these bases.

   $B=\langle \begin{pmatrix} 1 \\ -1 \end{pmatrix},\begin{pmatrix} 1 \\ 1 \end{pmatrix} \rangle \qquad D=\langle \begin{pmatrix} 2 \\ 2 \end{pmatrix},\begin{pmatrix} -1 \\ 1 \end{pmatrix} \rangle$

4. Using $B$ from the prior item, represent the transformation with respect to $B,B$.

Answer

Call the map $t:\mathbb{R}^2\to \mathbb{R}^2$.

1. To represent this map with respect to the standard bases, we must find, and then represent, the images of the vectors $\vec{e}_1$ and $\vec{e}_2$ from the domain's basis. The image of $\vec{e}_1$ is given. One way to find the image of $\vec{e}_2$ is by eye— we can see this.

   $\begin{pmatrix} 1 \\ 1 \end{pmatrix}-\begin{pmatrix} 1 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 1 \end{pmatrix} \;\stackrel{t}{\longmapsto}\; \begin{pmatrix} 2 \\ 0 \end{pmatrix}-\begin{pmatrix} -1 \\ 0 \end{pmatrix}=\begin{pmatrix} 3 \\ 0 \end{pmatrix}$

   A more systemmatic way to find the image of $\vec{e}_2$ is to use the given information to represent the transformation, and then use that representation to determine the image. Taking this for a basis,

   $C=\langle \begin{pmatrix} 1 \\ 1 \end{pmatrix},\begin{pmatrix} 1 \\ 0 \end{pmatrix} \rangle$

   the given information says this.

   ${\rm Rep}_{C,\mathcal{E}_2}(t) \begin{pmatrix} 2 &-1 \\ 0 &0 \end{pmatrix}$

   As

   ${\rm Rep}_{C}(\vec{e}_2)=\begin{pmatrix} 1 \\ -1 \end{pmatrix}_C$

   we have that

   ${\rm Rep}_{\mathcal{E}_2}(t(\vec{e}_2)) =\begin{pmatrix} 2 &-1 \\ 0 &0 \end{pmatrix}_{C,\mathcal{E}_2} \begin{pmatrix} 1 \\ -1 \end{pmatrix}_C =\begin{pmatrix} 3 \\ 0 \end{pmatrix}_{\mathcal{E}_2}$

   and consequently we know that $t(\vec{e}_2)=3\cdot\vec{e}_1$ (since, with respect to the standard basis, this vector is represented by itself). Therefore, this is the representation of $t$ with respect to $\mathcal{E}_2,\mathcal{E}_2$.

   ${\rm Rep}_{\mathcal{E}_2,\mathcal{E}_2}(t) =\begin{pmatrix} -1 &3 \\ 0 &0 \end{pmatrix}_{\mathcal{E}_2,\mathcal{E}_2}$

2. To use the matrix developed in the prior item, note that

   ${\rm Rep}_{\mathcal{E}_2}(\begin{pmatrix} 0 \\ 5 \end{pmatrix})=\begin{pmatrix} 0 \\ 5 \end{pmatrix}_{\mathcal{E}_2}$

   and so we have this is the representation, with respect to the codomain's basis, of the image of the given vector.

   ${\rm Rep}_{\mathcal{E}_2}(t(\begin{pmatrix} 0 \\ 5 \end{pmatrix})) =\begin{pmatrix} -1 &3 \\ 0 &0 \end{pmatrix}_{\mathcal{E}_2,\mathcal{E}_2} \begin{pmatrix} 0 \\ 5 \end{pmatrix}_{\mathcal{E}_2} =\begin{pmatrix} 15 \\ 0 \end{pmatrix}_{\mathcal{E}_2}$

   Because the codomain's basis is the standard one, and so vectors in the codomain are represented by themselves, we have this.

   $t(\begin{pmatrix} 0 \\ 5 \end{pmatrix}) =\begin{pmatrix} 15 \\ 0 \end{pmatrix}$

3. We first find the image of each member of $B$, and then represent those images with respect to $D$. For the first step, we can use the matrix developed earlier.

   ${\rm Rep}_{\mathcal{E}_2}(\begin{pmatrix} 1 \\-1 \end{pmatrix}) =\begin{pmatrix} -1 &3 \\ 0 &0 \end{pmatrix}_{\mathcal{E}_2,\mathcal{E}_2} \begin{pmatrix} 1 \\ -1 \end{pmatrix}_{\mathcal{E}_2} =\begin{pmatrix} -4 \\ 0 \end{pmatrix}_{\mathcal{E}_2} \quad\text{so}\quad t(\begin{pmatrix} 1 \\ -1 \end{pmatrix})=\begin{pmatrix} -4 \\ 0 \end{pmatrix}$

   Actually, for the second member of $B$ there is no need to apply the matrix because the problem statement gives its image.

   $t(\begin{pmatrix} 1 \\ 1 \end{pmatrix})=\begin{pmatrix} 2 \\ 0 \end{pmatrix}$

   Now representing those images with respect to $D$ is routine.

   ${\rm Rep}_{D}(\begin{pmatrix} -4 \\ 0 \end{pmatrix})=\begin{pmatrix} -1 \\ 2 \end{pmatrix}_D \quad\text{and}\quad {\rm Rep}_{D}(\begin{pmatrix} 2 \\ 0 \end{pmatrix})=\begin{pmatrix} 1/2 \\ -1 \end{pmatrix}_D$

   Thus, the matrix is this.

   ${\rm Rep}_{B,D}(t)= \begin{pmatrix} -1 &1/2 \\ 2 &-1 \end{pmatrix}_{B,D}$

4. We know the images of the members of the domain's basis from the prior item.

   $t(\begin{pmatrix} 1 \\ -1 \end{pmatrix})=\begin{pmatrix} -4 \\ 0 \end{pmatrix} \qquad t(\begin{pmatrix} 1 \\ 1 \end{pmatrix})=\begin{pmatrix} 2 \\ 0 \end{pmatrix}$

   We can compute the representation of those images with respect to the codomain's basis.

   ${\rm Rep}_{B}(\begin{pmatrix} -4 \\ 0 \end{pmatrix})=\begin{pmatrix} -2 \\ -2 \end{pmatrix}_B \quad\text{and}\quad {\rm Rep}_{B}(\begin{pmatrix} 2 \\ 0 \end{pmatrix})=\begin{pmatrix} 1 \\ 1 \end{pmatrix}_B$

   Thus this is the matrix.

   ${\rm Rep}_{B,B}(t)= \begin{pmatrix} -2 &1 \\ -2 &1 \end{pmatrix}_{B,B}$

Problem 13

Suppose that $h:V\to W$ is nonsingular so that by Theorem II.2.21, for any basis $B=\langle \vec{\beta}_1,\dots,\vec{\beta}_n \rangle \subset V$ the image $h(B)=\langle h(\vec{\beta}_1),\dots,h(\vec{\beta}_n) \rangle$ is a basis for $W$.

1. Represent the map $h$ with respect to $B,h(B)$.
2. For a member $\vec{v}$ of the domain, where the representation of $\vec{v}$ has components $c_1$, ..., $c_n$, represent the image vector $h(\vec{v})$ with respect to the image basis $h(B)$.

Answer

1. The images of the members of the domain's basis are

   $\vec{\beta}_1\mapsto h(\vec{\beta}_1) \quad \vec{\beta}_2\mapsto h(\vec{\beta}_2) \quad\ldots\quad \vec{\beta}_n\mapsto h(\vec{\beta}_n)$

   and those images are represented with respect to the codomain's basis in this way.

   ${\rm Rep}_{h(B)}(\,h(\vec{\beta}_1)\,)=\begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} \quad {\rm Rep}_{h(B)}(\,h(\vec{\beta}_2)\,)=\begin{pmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{pmatrix} \quad\ldots\quad {\rm Rep}_{h(B)}(\,h(\vec{\beta}_n)\,)=\begin{pmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{pmatrix}$

   Hence, the matrix is the identity.

   ${\rm Rep}_{B,h(B)}(h) =\begin{pmatrix} 1 &0 &\ldots &0 \\ 0 &1 & &0 \\ & &\ddots \\ 0 &0 & &1 \end{pmatrix}$

2. Using the matrix in the prior item, the representation is this.

   ${\rm Rep}_{h(B)}(\,h(\vec{v})\,) =\begin{pmatrix} c_1 \\ \vdots \\ c_n \end{pmatrix}_{h(B)}$

Problem 14

Give a formula for the product of a matrix and $\vec{e}_i$, the column vector that is all zeroes except for a single one in the $i$-th position.

Answer

The product

$\begin{pmatrix} h_{1,1} &\ldots &h_{1,i} &\ldots &h_{1,n} \\ h_{2,1} &\ldots &h_{2,i} &\ldots &h_{2,n} \\ &\vdots \\ h_{m,1} &\ldots &h_{m,i} &\ldots &h_{1,n} \end{pmatrix} \begin{pmatrix} 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \end{pmatrix} = \begin{pmatrix} h_{1,i} \\ h_{2,i} \\ \vdots \\ h_{m,i} \end{pmatrix}$

gives the $i$-th column of the matrix.

This exercise is recommended for all readers.

Problem 15

For each vector space of functions of one real variable, represent the derivative transformation with respect to $B,B$.

1. $\{a\cos x+b\sin x \,\big|\, a,b\in\mathbb{R}\}$, $B=\langle \cos x,\sin x \rangle$
2. $\{ae^x+be^{2x} \,\big|\, a,b\in\mathbb{R}\}$, $B=\langle e^x,e^{2x} \rangle$
3. $\{a+bx+ce^x+dxe^{x} \,\big|\, a,b,c,d\in\mathbb{R}\}$, $B=\langle 1,x,e^x,xe^{x} \rangle$

Answer

1. The images of the basis vectors for the domain are $\cos x\stackrel{d/dx}{\longmapsto}-\sin x$ and $\sin x\stackrel{d/dx}{\longmapsto}\cos x$. Representing those with respect to the codomain's basis (again, $B$) and adjoining the representations gives this matrix.

   ${\rm Rep}_{B,B}(\frac{d}{dx})= \begin{pmatrix} 0 &1 \\ -1 &0 \end{pmatrix}_{B,B}$

2. The images of the vectors in the domain's basis are $e^x\stackrel{d/dx}{\longmapsto}e^x$ and $e^{2x}\stackrel{d/dx}{\longmapsto}2e^{2x}$. Representing with respect to the codomain's basis and adjoining gives this matrix.

   ${\rm Rep}_{B,B}(\frac{d}{dx})= \begin{pmatrix} 1 &0 \\ 0 &2 \end{pmatrix}_{B,B}$

3. The images of the members of the domain's basis are $1\stackrel{d/dx}{\longmapsto}0$, $x\stackrel{d/dx}{\longmapsto}1$, $e^{x}\stackrel{d/dx}{\longmapsto}e^{x}$, and $xe^{x}\stackrel{d/dx}{\longmapsto}e^x+xe^x$. Representing these images with respect to $B$ and adjoining gives this matrix.

   ${\rm Rep}_{B,B}(\frac{d}{dx})= \begin{pmatrix} 0 &1 &0 &0 \\ 0 &0 &0 &0 \\ 0 &0 &1 &1 \\ 0 &0 &0 &1 \end{pmatrix}_{B,B}$

Problem 16

Find the range of the linear transformation of $\mathbb{R}^2$ represented with respect to the standard bases by each matrix.

1. $\begin{pmatrix} 1 &0 \\ 0 &0 \end{pmatrix}$
2. $\begin{pmatrix} 0 &0 \\ 3 &2 \end{pmatrix}$
3. a matrix of the form $\begin{pmatrix} a &b \\ 2a &2b \end{pmatrix}$

Answer

1. It is the set of vectors of the codomain represented with respect to the codomain's basis in this way.

   $\{ \begin{pmatrix} 1 &0 \\ 0 &0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \,\big|\, x,y\in\mathbb{R}\} =\{\begin{pmatrix} x \\ 0 \end{pmatrix} \,\big|\, x,y\in\mathbb{R}\}$

   As the codomain's basis is $\mathcal{E}_2$, and so each vector is represented by itself, the range of this transformation is the $x$-axis.
2. It is the set of vectors of the codomain represented in this way.

   $\{ \begin{pmatrix} 0 &0 \\ 3 &2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \,\big|\, x,y\in\mathbb{R}\} =\{\begin{pmatrix} 0 \\ 3x+2y \end{pmatrix} \,\big|\, x,y\in\mathbb{R}\}$

   With respect to $\mathcal{E}_2$ vectors represent themselves so this range is the $y$ axis.
3. The set of vectors represented with respect to $\mathcal{E}_2$ as

   $\{ \begin{pmatrix} a &b \\ 2a &2b \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \,\big|\, x,y\in\mathbb{R}\} =\{\begin{pmatrix} ax+by \\ 2ax+2by \end{pmatrix} \,\big|\, x,y\in\mathbb{R}\} =\{(ax+by)\cdot\begin{pmatrix} 1 \\ 2 \end{pmatrix} \,\big|\, x,y\in\mathbb{R}\}$

   is the line $y=2x$, provided either $a$ or $b$ is not zero, and is the set consisting of just the origin if both are zero.

This exercise is recommended for all readers.

Problem 17

Can one matrix represent two different linear maps? That is, can ${\rm Rep}_{B,D}(h)={\rm Rep}_{\hat{B},\hat{D}}(\hat{h})$?

Answer

Yes, for two reasons.

First, the two maps $h$ and $\hat{h}$ need not have the same domain and codomain. For instance,

$\begin{pmatrix} 1 &2 \\ 3 &4 \end{pmatrix}$

represents a map $h:\mathbb{R}^2\to \mathbb{R}^2$ with respect to the standard bases that sends

$\begin{pmatrix} 1 \\ 0 \end{pmatrix}\mapsto\begin{pmatrix} 1 \\ 3 \end{pmatrix} \quad\text{and}\quad \begin{pmatrix} 0 \\ 1 \end{pmatrix}\mapsto\begin{pmatrix} 2 \\ 4 \end{pmatrix}$

and also represents a $\hat{h}:\mathcal{P}_1\to \mathbb{R}^2$ with respect to $\langle 1,x \rangle$ and $\mathcal{E}_2$ that acts in this way.

$1\mapsto\begin{pmatrix} 1 \\ 3 \end{pmatrix} \quad\text{and}\quad x\mapsto\begin{pmatrix} 2 \\ 4 \end{pmatrix}$

The second reason is that, even if the domain and codomain of $h$ and $\hat{h}$ coincide, different bases produce different maps. An example is the $2 \! \times \! 2$ identity matrix

$I=\begin{pmatrix} 1 &0 \\ 0 &1 \end{pmatrix}$

which represents the identity map on $\mathbb{R}^2$ with respect to $\mathcal{E}_2,\mathcal{E}_2$. However, with respect to $\mathcal{E}_2$ for the domain but the basis $D=\langle \vec{e}_2,\vec{e}_1 \rangle$ for the codomain, the same matrix $I$ represents the map that swaps the first and second components

$\begin{pmatrix} x \\ y \end{pmatrix}\mapsto\begin{pmatrix} y \\ x \end{pmatrix}$

(that is, reflection about the line $y=x$).

Problem 18

Prove Theorem 1.4.

Answer

We mimic Example 1.1, just replacing the numbers with letters.

Write $B$ as $\langle \vec{\beta}_1,\ldots,\vec{\beta}_n \rangle$ and $D$ as $\langle \vec{\delta}_1,\dots,\vec{\delta}_m \rangle$. By definition of representation of a map with respect to bases, the assumption that

${\rm Rep}_{B,D}(h) =\begin{pmatrix} h_{1,1} &\ldots &h_{1,n} \\ \vdots & &\vdots \\ h_{m,1} &\ldots &h_{m,n} \end{pmatrix}$

means that $h(\vec{\beta}_i)=h_{i,1}\vec{\delta}_1+\dots+h_{i,n}\vec{\delta}_n$. And, by the definition of the representation of a vector with respect to a basis, the assumption that

${\rm Rep}_{B}(\vec{v})=\begin{pmatrix} c_1 \\ \vdots \\ c_n \end{pmatrix}$

means that $\vec{v}=c_1\vec{\beta}_1+\cdots+c_n\vec{\beta}_n$. Substituting gives

$\begin{array}{rl} h(\vec{v}) &=h(c_1\cdot\vec{\beta}_1+\dots+c_n\cdot\vec{\beta}_n) \\ &=c_1\cdot h(\vec{\beta}_1)+\dots+c_n\cdot \vec{\beta}_n \\ &=c_1\cdot (h_{1,1}\vec{\delta}_1+\dots+h_{m,1}\vec{\delta}_m) +\dots +c_n\cdot (h_{1,n}\vec{\delta}_1+\dots+h_{m,n}\vec{\delta}_m) \\ &=(h_{1,1}c_1+\dots+h_{1,n}c_n)\cdot\vec{\delta}_1 +\cdots +(h_{m,1}c_1+\dots+h_{m,n}c_n)\cdot\vec{\delta}_m \end{array}$

and so $h(\vec{v})$ is represented as required.

This exercise is recommended for all readers.

Problem 19

Example 1.8 shows how to represent rotation of all vectors in the plane through an angle $\theta$ about the origin, with respect to the standard bases.

1. Rotation of all vectors in three-space through an angle $\theta$ about the $x$-axis is a transformation of $\mathbb{R}^3$. Represent it with respect to the standard bases. Arrange the rotation so that to someone whose feet are at the origin and whose head is at $(1,0,0)$, the movement appears clockwise.
2. Repeat the prior item, only rotate about the $y$-axis instead. (Put the person's head at $\vec{e}_2$.)
3. Repeat, about the $z$-axis.
4. Extend the prior item to $\mathbb{R}^4$. (Hint: "rotate about the $z$-axis" can be restated as "rotate parallel to the $xy$-plane".)

Answer

1. The picture is this.

   

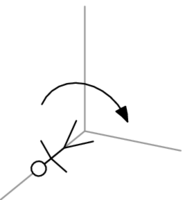
   The images of the vectors from the domain's basis

   $\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\mapsto\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \qquad \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\mapsto\begin{pmatrix} 0 \\ \cos\theta \\ -\sin\theta \end{pmatrix} \qquad \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\mapsto\begin{pmatrix} 0 \\ \sin\theta \\ \cos\theta \end{pmatrix}$

   are represented with respect to the codomain's basis (again, $\mathcal{E}_3$) by themselves, so adjoining the representations to make the matrix gives this.

   ${\rm Rep}_{\mathcal{E}_3,\mathcal{E}_3}(r_\theta)= \begin{pmatrix} 1 &0 &0 \\ 0 &\cos\theta &\sin\theta \\ 0 &-\sin\theta &\cos\theta \end{pmatrix}$

2. The picture is similar to the one in the prior answer. The images of the vectors from the domain's basis

   $\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\mapsto\begin{pmatrix} \cos\theta \\ 0 \\ \sin\theta \end{pmatrix} \qquad \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\mapsto\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \qquad \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\mapsto\begin{pmatrix} -\sin\theta \\ 0 \\ \cos\theta \end{pmatrix}$

   are represented with respect to the codomain's basis $\mathcal{E}_3$ by themselves, so this is the matrix.

   $\begin{pmatrix} \cos\theta &0 &-\sin\theta \\ 0 &1 &0 \\ \sin\theta &0 &\cos\theta \end{pmatrix}$

3. To a person standing up, with the vertical $z$-axis, a rotation of the $xy$-plane that is clockwise proceeds from the positive $y$-axis to the positive $x$-axis. That is, it rotates opposite to the direction in Example 1.8. The images of the vectors from the domain's basis

   $\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\mapsto\begin{pmatrix} \cos\theta \\ -\sin\theta \\ 0 \end{pmatrix} \qquad \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\mapsto\begin{pmatrix} \sin\theta \\ \cos\theta \\ 0 \end{pmatrix} \qquad \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\mapsto\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$

   are represented with respect to $\mathcal{E}_3$ by themselves, so the matrix is this.

   $\begin{pmatrix} \cos\theta &\sin\theta &0 \\ -\sin\theta &\cos\theta &0 \\ 0 &0 &1 \end{pmatrix}$

4. $\begin{pmatrix} \cos\theta &\sin\theta &0 &0 \\ -\sin\theta &\cos\theta &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1 \end{pmatrix}$

Problem 20 (Schur's Triangularization Lemma)

1. Let $U$ be a subspace of $V$ and fix bases $B_U\subseteq B_V$. What is the relationship between the representation of a vector from $U$ with respect to $B_U$ and the representation of that vector (viewed as a member of $V$) with respect to $B_V$?
2. What about maps?
3. Fix a basis $B=\langle \vec{\beta}_1,\dots,\vec{\beta}_n \rangle$ for $V$ and observe that the spans

   $[\{\vec{0}\}]=\{\vec{0}\}\subset[\{\vec{\beta}_1\}] \subset[\{\vec{\beta}_1,\vec{\beta}_2\}] \subset \quad\cdots\quad \subset[B]=V$

   form a strictly increasing chain of subspaces. Show that for any linear map $h:V\to W$ there is a chain $W_0=\{\vec{0}\}\subseteq W_1\subseteq \dots \subseteq W_m =W$ of subspaces of $W$ such that

   $h([\{\vec{\beta}_1,\dots,\vec{\beta}_i\}])\subset W_i$

   for each $i$.
4. Conclude that for every linear map $h:V\to W$ there are bases $B,D$ so the matrix representing $h$ with respect to $B,D$ is upper-triangular (that is, each entry $h_{i,j}$ with $i>j$ is zero).
5. Is an upper-triangular representation unique?

Answer

1. Write $B_U$ as $\langle \vec{\beta}_1,\dots,\vec{\beta}_k \rangle$ and then $B_V$ as $\langle \vec{\beta}_1,\dots,\vec{\beta}_k, \vec{\beta}_{k+1},\dots,\vec{\beta}_n \rangle$. If

   ${\rm Rep}_{B_U}(\vec{v})=\begin{pmatrix} c_1 \\ \vdots \\ c_k \end{pmatrix} \qquad\text{so that } \vec{v}=c_1\cdot\vec{\beta}_1+\cdots+c_k\cdot\vec{\beta}_k$

   then,

   ${\rm Rep}_{B_V}(\vec{v})=\begin{pmatrix} c_1 \\ \vdots\\ c_k \\ 0 \\ \vdots \\ 0 \end{pmatrix}$

   because $\vec{v}=c_1\cdot\vec{\beta}_1+\dots+c_k\cdot\vec{\beta}_k +0\cdot\vec{\beta}_{k+1}+\dots+0\cdot\vec{\beta}_n$.
2. We must first decide what the question means. Compare $h:V\to W$ with its restriction to the subspace ${h}\mathpunct\upharpoonright_{U}:U\to W$. The rangespace of the restriction is a subspace of $W$, so fix a basis $D_{h(U)}$ for this rangespace and extend it to a basis $D_V$ for $W$. We want the relationship between these two.

   ${\rm Rep}_{B_V,D_V}(h) \quad\text{and}\quad {\rm Rep}_{B_U,D_{h(U)}}({h}\mathpunct\upharpoonright_{U})$

   The answer falls right out of the prior item: if

   ${\rm Rep}_{B_U,D_{h(U)}}({h}\mathpunct\upharpoonright_{U}) =\begin{pmatrix} h_{1,1} &\ldots &h_{1,k} \\ \vdots & &\vdots \\ h_{p,1} &\ldots &h_{p,k} \end{pmatrix}$

   then the extension is represented in this way.

   ${\rm Rep}_{B_V,D_V}(h) =\begin{pmatrix} h_{1,1} &\ldots &h_{1,k} &h_{1,k+1} &\ldots &h_{1,n} \\ \vdots & & & & &\vdots \\ h_{p,1} &\ldots &h_{p,k} &h_{p,k+1} &\ldots &h_{p,n} \\ 0 &\ldots &0 &h_{p+1,k+1}&\ldots &h_{p+1,n} \\ \vdots & & & & &\vdots \\ 0 &\ldots &0 &h_{m,k+1} &\ldots &h_{m,n} \end{pmatrix}$

3. Take $W_i$ to be the span of $\{h(\vec{\beta}_1),\dots,h(\vec{\beta}_i)\}$.
4. Apply the answer from the second item to the third item.
5. No. For instance $\pi_x:\mathbb{R}^2\to \mathbb{R}^2$, projection onto the $x$ axis, is represented by these two upper-triangular matrices

   ${\rm Rep}_{\mathcal{E}_2,\mathcal{E}_2}(\pi_x)= \begin{pmatrix} 1 &0 \\ 0 &0 \end{pmatrix} \quad\text{and}\quad {\rm Rep}_{C,\mathcal{E}_2}(\pi_x)= \begin{pmatrix} 0 &1 \\ 0 &0 \end{pmatrix}$

   where $C=\langle \vec{e}_2,\vec{e}_1 \rangle$.