Geometry for Elementary School/Bisecting an angle

BISECT ANGLE $\angle ABC$

1. Use a compass to find points D and E, equidistant from the vertex, point B.
2. Draw the line $\overline{DE}$.
   
   
   
   
3. Construct an equilateral triangle on $\overline{DE}$ with third vertex F and get $\triangle DEF$. (Lines DF and EF are equal in length).
   
   
   
   
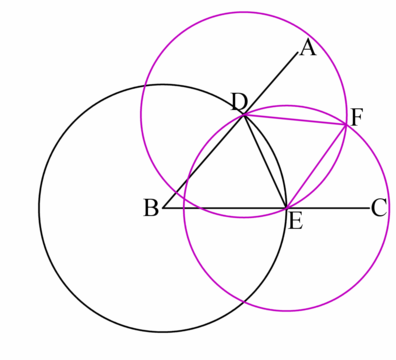
4. Draw the line $\overline{BF}$.
   
   
   
   

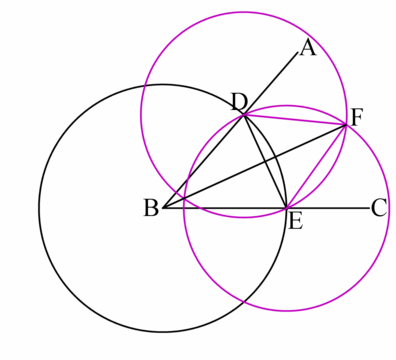
Claim

1. The angles $\angle ABF$, $\angle FBC$ equal to half of $\angle ABC$.

The proof

1. $\overline{DE}$ is a segment from the center to the circumference of $\circ B,\overline{BD}$ and therefore equals its radius.
2. Hence, $\overline{BE}$ equals $\overline{BD}$.
3. $\overline{DF}$ and $\overline{EF}$ are sides of the equilateral triangle $\triangle DEF$.
4. Hence, $\overline{DF}$ equals $\overline{EF}$.
5. The segment $\overline{BF}$ equals to itself
6. Due to the Side-Side-Side congruence theorem the triangles $\triangle ABF$ and $\triangle FBC$ congruent.
7. Hence, the angles $\angle ABF$, $\angle FBC$ equal to half of $\angle ABC$.

Note

We showed a simple method to divide an angle to two. A natural question that rises is how to divide an angle into other numbers. Since Euclid's days, mathematicians looked for a method for trisecting an angle, dividing it into 3. Only after years of trials it was proven that no such method exists since such a construction is impossible, using only ruler and compass.

Exercise

1. Find a construction for dividing an angle to 4.
2. Find a construction for dividing an angle to 8.
3. For which other number you can find such constructions?