Geometry/Chapter 7
Section 7.1 - Parallel Lines
[edit | edit source]In Euclidean Geometry, lines are parallel if they do not intersect.
Remember that lines extend infinitely, if they are not parallel they will eventually intersect.
Exercises
[edit | edit source]draw line AB, draw a line CD that is parallel to AB
find a way to prove that AB is parallel to CD
Section 7.2 - Perpendicular Lines
[edit | edit source]In Euclidean Geometry, lines are perpendicular if they intersect at a 90 degree angle.

Exercises
[edit | edit source]Draw a line AB, then pick a point C on line AB, make a line which intersects C and is perpendicular to AB, i.e.,
prove that line CD is perpendicular to AB.
Section 7.3 - Circles
[edit | edit source]Circles
[edit | edit source]Congruent Circles
[edit | edit source]Congruent circles are circles that have the same size, that is, the same radius.
Concentric Circles
[edit | edit source]Concentric Circles share the same center, axis or origin with one inside the other. Concentric Circles do not necessarily have the same radius.
Exercises
[edit | edit source]draw a circle, find a way to draw a congruent circle, prove they are congruent
draw a circle, then draw a concentric one, prove that they are concentric.
Radius, Diameter, Chord
[edit | edit source]A radius is a line segment connecting a point on the circle and the center of the circle.
Diameter is a line segment connecting 2 points on the circle and goes through the center.
A chord is a line segment connecting 2 points on the circle that does not have to go through the center. The diameter of a circle is the longest chord.
Section 7.4 - Quadrilaterals
[edit | edit source]A quadrilateral is defined as any 4 sided polygon. This means squares, rectangles, etc. are all called quadrilaterals. In the following sections we will take a closer look at each of the important quadrilaterals, how they are defined, and some special properties of each of them.
Rectangles
[edit | edit source]A Rectangle is defined by having 4 conditions. The first is that it is a 4 sided polygon. The second is that it has 2 pairs of parallel sides. The third is that the pairs of parallel sides are of equal length. The forth is that all angles must be equal to 90 degrees or a right angle.
Lets take an example. Below is a Rectangle. First we note that it has 4 sides, and that they form a polygon, this makes it a 4 sided polygon so the first condition is satisfied. Next we notice that 2 of the sides are parallel to each other and that the other 2 sides are parallel to each other, thus the second condition has been meet. Now we notice that the pairs of parallel sides are of equal length, thus the third condition has been meet. The final condition was that all angles must be 90 degrees, as shown in the image they are in fact 90 degrees. Because all 4 conditions have been meet we now know that the polygon below is in fact a Rectangle.
Special Properties
[edit | edit source]
Ok, now that the rectangle has been defined we need to know whats so special about rectangles.
Length of a diagonal:
Below is the same rectangle as above except it has the diagonal drawn from 1 vertex to the other. The length of this diagonal is equal to the square root of one side squared added to the length of the adjacent side squared. e.g.
The proof of this is quite simple. But first you have to know the pythagorean theorem so read over this if you don't already know it.
1) Angle ABC = 90 degrees - given in the definition of a rectangle.
2) Side AB and side BC and the diagonal form a triangle. - a 3 sided polygon
3) The triangle is also a right angled triangle because it has a right angle in it. - angle ABC
4) The diagonal of the rectangle is the hypotenuse of the triangle.
5) the hypotenuse of a right angled triangle is equal to the square root of the sum of the squares of the sides - Pythagora's theorem
6) thus the diagonal is equal to
Following this property we can note that if we draw a diagonal we create 2 congruent triangles inside the rectangle.
proof:
below is such a Rectangle with the diagonal drawn. We shall name the vertices A, B, C, D. The diagonal is called AC because the 2 endpoints are A and C. The 2 triangles are ABC and ADC.

1) The 2 triangles share the a side - AC.
2) AD and BC have an equal length - given.
3) angles ABC and ADC are of equal measure - definition of a rectangle.
4) Each triangle has an angle of equal measure - statement 3.
5) by the side angle side theorem each triangle is congruent.
Examples
[edit | edit source]Square
[edit | edit source]A square has the same properties as a rectangle except that all 4 sides must be equal length. A square is also considered a rhombus, kite, parallelogram, and trapezoid.
Special Properties
[edit | edit source]Examples
[edit | edit source]Trapezoid
[edit | edit source]A Trapezoid is a quadrilateral with 2 sides that are parallel.

Special Properties
[edit | edit source]Area for a trapezoid is given by the formula:
, where a and b are the lengths of the 2 parallel sides and h is the height.
Examples
[edit | edit source]<1=
Rhombus
[edit | edit source]A Rhombus is a quadrilateral with four equal sides.

Special Properties
[edit | edit source]The area of a Rhombus is given by the formula:
where D1 and D2 are the lengths of the two diagonals
Because the rhombus is a parallelogram, the area also equals the length of a side (B) multiplied by the perpendicular distance between two opposite sides(H)
The area also equals the square of the side multiplied by the sine of any of the interior angles:
where a is the length of the side and is the angle between two sides.
Examples
[edit | edit source]Parallelogram
[edit | edit source]A Parallelogram is a quadrilateral with two sets of parallel sides.
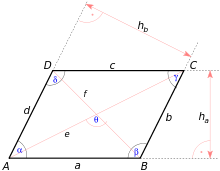
Special Properties
[edit | edit source]The Area of a parallelogram:
- where B is the Base and H is the Height
The Diagonals of a parallelogram bisect each other.
Example
[edit | edit source]Exercises
[edit | edit source]Chapter Review
[edit | edit source]Vocabulary
[edit | edit source]Navigation
- Geometry Main Page
- Motivation
- Introduction
- Geometry/Chapter 1 - HS Definitions and Reasoning (Introduction)
- Geometry/Chapter 1/Lesson 1 Introduction
- Geometry/Chapter 1/Lesson 2 Reasoning
- Geometry/Chapter 1/Lesson 3 Undefined Terms
- Geometry/Chapter 1/Lesson 4 Axioms/Postulates
- Geometry/Chapter 1/Lesson 5 Theorems
- Geometry/Chapter 1/Vocabulary Vocabulary
- Geometry/Chapter 2 Proofs
- Geometry/Chapter 3 Logical Arguments
- Geometry/Chapter 4 Congruence and Similarity
- Geometry/Chapter 5 Triangle: Congruence and Similiarity
- Geometry/Chapter 6 Triangle: Inequality Theorem
- Geometry/Chapter 7 Parallel Lines, Quadrilaterals, and Circles
- Geometry/Chapter 8 Perimeters, Areas, Volumes
- Geometry/Chapter 9 Prisms, Pyramids, Spheres
- Geometry/Chapter 10 Polygons
- Geometry/Chapter 11
- Geometry/Chapter 12 Angles: Interior and Exterior
- Geometry/Chapter 13 Angles: Complementary, Supplementary, Vertical
- Geometry/Chapter 14 Pythagorean Theorem: Proof
- Geometry/Chapter 15 Pythagorean Theorem: Distance and Triangles
- Geometry/Chapter 16 Constructions
- Geometry/Chapter 17 Coordinate Geometry
- Geometry/Chapter 18 Trigonometry
- Geometry/Chapter 19 Trigonometry: Solving Triangles
- Geometry/Chapter 20 Special Right Triangles
- Geometry/Chapter 21 Chords, Secants, Tangents, Inscribed Angles, Circumscribed Angles
- Geometry/Chapter 22 Rigid Motion
- Geometry/Appendix A Formulae
- Geometry/Appendix B Answers to problems
- Appendix C. Geometry/Postulates & Definitions
- Appendix D. Geometry/The SMSG Postulates for Euclidean Geometry
















