Geometry/Chapter 16
A construction is when one constructs a figure (such as a square, an angle bisector, etc.) with a compass and a straightedge.
Constructing a Congruent Segment to a Given Segment
[edit | edit source]To Construct a congruent segment to a given segment, set your compass to the both endpoints of the given segment. Then from a starting point on the second line mark off the same distance using your compass. This segment is congruent to the given segment.
Equilateral Triangle
[edit | edit source]An example of a construction would be the construction of an equilateral triangle with two intersecting circles. Two circles are drawn with the same radius with a point from each circle intersecting the radius of the other circle.
Then lines are drawn from the radii to the intersection of the two circles and between the two radii.
Now we have an equilateral triangle.
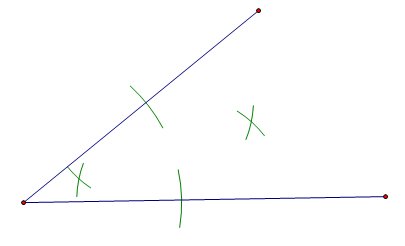
Angle Bisector
[edit | edit source]To Construct an angle Bisector: 1. Put the center of the compass on the angle and mark an intersection on each line.
2. Put the center of the compass on one of the marked intersections and then mark two spots near the center. Repeat this step on the other intersection.
3. Draw a line connecting the points of intersection and the angle.
Perpendicular Bisector
[edit | edit source]To construct the perpendicular bisector of a segment given the segment AB, first draw a circle centered at point A. Next draw with your compass a circle with the same radius as the first circle but centered at point B. Lastly, connect the points, called C and D where the two circles intersect. This segment is the perpendicular bisector. Reasoning: Any point that is the same distance from the endpoints of a segment lies on the perpendicular bisector of that segment. Given two such points you can draw that line.
Image:PerpendicularBisector2JPEG.jpg
Constructing a Congruent Angle to a Given Angle
[edit | edit source]To construct a congruent angle to a given angle first draw a segment on which you are going to construct the congruent angle. Place a point on this segment that will be the vertex point of the new congruent angle. Draw an arc(part of a circle) that crosses both sides of the original angle. Then using the same setting as for this arc draw an arc from the point on the segment so that this arc has the same radius as the previous arc. next use your compass to measure the distance between the points where the first arc crosses the sides of the angle. Now going to the second arc with the same setting mark the same distance on this arc as on the first arc. Connect this point with the original point on the segment.
Constructing a Perpendicular Line through a Point on a Line
[edit | edit source]Given a point on a line, first draw a circle using this point as its center. Using the two points where the circle intersects the line draw two congruent arcs that intersect each other. This point is equal distance from both endpoints of the circle and thus on its perpendicular bisector as is the original point. Connect these two points to complete the construction.
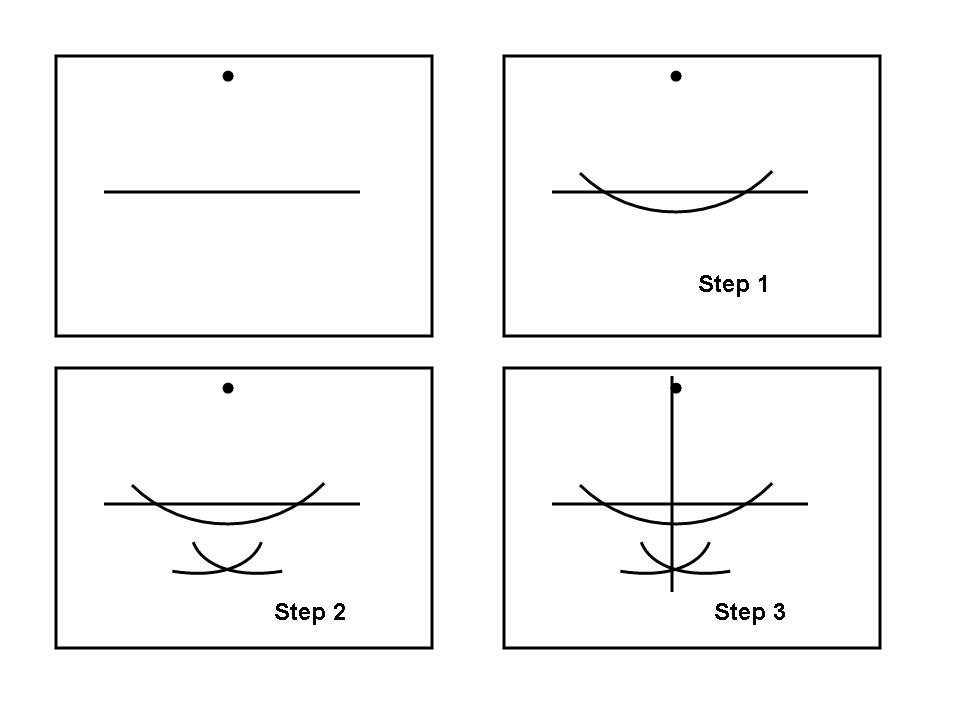
Constructing a Perpendicular to a Line From a Point Not on That Line
[edit | edit source]To construct a perpendicular to a line from a point not on that line, use the point as the center of an arc that intersects the line in two points. Your original point will lie on the perpendicular bisector of the segment formed by these two new points. Using these points as the centers of two congruent arcs that intersect one another you get another point on this same perpendicular bisector. Connect this new point with your original point to finish this construction.
Constructing a Triangle congruent to a Given Triangle(SSS Method)
[edit | edit source]To construct a triangle congruent to a given triangle, first construct a base side in the same way as constructing a congruent segment. Measuring a second side of the given triangle with the compass draw an arc from one end of the constructed segment. Setting the compass to the length of the third side of the given triangle go to the second point of the constructed segment and draw another arc whose radius is the same as the third side and intersects the first arc. Connect this point of intersection with the endpoints of the constructed segment to finish the congruent triangle.
Constructing a Triangle Congruent to a Given Triangle (the SAS Method)
[edit | edit source]To construct a Triangle congruent to a given triangle using the Side Angle Side method, you must first construct an angle congruent to one of the given angles of the first triangle. Then use the compass to measure one of the sides of the first triangle that is next to the angle and then measure the new side next to the new angle. Then measure the side on the other side of the angle of the first triangle and use it to construct the other side of the new triangle. Connect these two constructed points to make the third side of the new triangle.
Exercise
[edit | edit source]Navigation
- Geometry Main Page
- Motivation
- Introduction
- Geometry/Chapter 1 - HS Definitions and Reasoning (Introduction)
- Geometry/Chapter 1/Lesson 1 Introduction
- Geometry/Chapter 1/Lesson 2 Reasoning
- Geometry/Chapter 1/Lesson 3 Undefined Terms
- Geometry/Chapter 1/Lesson 4 Axioms/Postulates
- Geometry/Chapter 1/Lesson 5 Theorems
- Geometry/Chapter 1/Vocabulary Vocabulary
- Geometry/Chapter 2 Proofs
- Geometry/Chapter 3 Logical Arguments
- Geometry/Chapter 4 Congruence and Similarity
- Geometry/Chapter 5 Triangle: Congruence and Similiarity
- Geometry/Chapter 6 Triangle: Inequality Theorem
- Geometry/Chapter 7 Parallel Lines, Quadrilaterals, and Circles
- Geometry/Chapter 8 Perimeters, Areas, Volumes
- Geometry/Chapter 9 Prisms, Pyramids, Spheres
- Geometry/Chapter 10 Polygons
- Geometry/Chapter 11
- Geometry/Chapter 12 Angles: Interior and Exterior
- Geometry/Chapter 13 Angles: Complementary, Supplementary, Vertical
- Geometry/Chapter 14 Pythagorean Theorem: Proof
- Geometry/Chapter 15 Pythagorean Theorem: Distance and Triangles
- Geometry/Chapter 16 Constructions
- Geometry/Chapter 17 Coordinate Geometry
- Geometry/Chapter 18 Trigonometry
- Geometry/Chapter 19 Trigonometry: Solving Triangles
- Geometry/Chapter 20 Special Right Triangles
- Geometry/Chapter 21 Chords, Secants, Tangents, Inscribed Angles, Circumscribed Angles
- Geometry/Chapter 22 Rigid Motion
- Geometry/Appendix A Formulae
- Geometry/Appendix B Answers to problems
- Appendix C. Geometry/Postulates & Definitions
- Appendix D. Geometry/The SMSG Postulates for Euclidean Geometry