General Mechanics/Torque and Angular Momentum
Torque
[edit | edit source]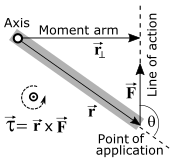
Torque is the action of a force on a mass which induces it to revolve about some point, called the origin. It is defined as
where is the position of the mass relative to the origin.
Notice that the torque is 0 in a number of circumstances. If the force points directly toward or away from the origin, the cross product is zero, resulting in zero torque, even though the force is non-zero. Likewise, if , the torque is 0. Thus, a force acting at the origin produces no torque. Both of these limits make sense intuitively, since neither induces the mass to revolve around the origin.
Angular momentum
[edit | edit source]The angular momentum of a mass relative to a point O is defined as
where p is the ordinary (also called "linear") momentum of the mass. The angular momentum is 0 if the motion of the object is directly towards or away from the origin, or if it is located at the origin.
If we take the cross product of the position vector and Newton's second law, we obtain an equation that relates torque and angular momentum:
Since the cross product of parallel vectors is zero, this simplifies to
This is the rotational version of Newton's second law.
For both torque and angular momentum the location of the origin is arbitrary, and is generally chosen for maximum convenience. However, it is necessary to choose the same origin for both the torque and the angular momentum.
For the case of a central force, i.e. one which acts along the line of centers between two objects (such as gravity), there often exists a particularly convenient choice of origin. If the origin is placed at the center of the sun (which is assumed not to move under the influence of the planet's gravity), then the torque exerted on the planet by the sun's gravity is 0, which means that the angular momentum of the planet about the center of the sun is constant in time. No other choice of origin would yield this convenient result.
We already know about two fundamental conservation laws—those of energy and linear momentum. We believe that angular momentum is similarly conserved in isolated systems. In other words, particles can exchange angular momentum between themselves, but the vector sum of the angular momentum of all the particles in a system isolated from outside influences must remain constant.
In the modern view, conservation of angular momentum is a consequence of the isotropy of space—i.e. the properties of space don't depend on direction. This is in direct analogy with conservation of ordinary momentum, which we recall is a consequence of the homogeneity of space.
Angular velocity and centrifugal force
[edit | edit source]If an object is rotating about an axis, being a unit vector, at frequency we say it has angular velocity . Despite the name, this is not the rate of change of an angle, nor even of a vector.
If a constant vector is rotating with angular velocity about a fixed point then
This says the acceleration is always at right angles to both the velocity and the axis of rotation.
When the axis is changing can be defined as the vector which makes this true.
Note that on the left hand side of this equation is a vector in a fixed coordinate system with variable components but on the right hand side its components are given in a moving coordinate system, where they are fixed.
We can distinguish them more clearly by using subscripts, for rotating and for fixed, then extend this to arbitrary vectors
for any vector
Using this, we can write Newton's second law in the rotating frame.
or, rearranging
The mass behaves as if there were two additional forces acting on it. The first term, is called the Coriolis force. The second term is recognizable as the familiar centrifugal force.

















