General Chemistry/The Quantum Atom
The Quantum Numbers
[edit | edit source]These four numbers are used to describe the location of an electron in an atom.
| Number | Symbol | Possible Values |
|---|---|---|
| Principal Quantum Number | ||
| Angular Momentum Quantum Number | ||
| Magnetic Quantum Number | ||
| Spin Quantum Number |
Principal Quantum Number (n)
[edit | edit source]Determines the shell the electron is in. The shell is the main component that determines the energy of the electron (higher n corresponds to higher energy), as well as size of the orbital, corresponding to maximum nuclear distance (higher n means further possible distance from the nucleus). The row that an element is placed on the periodic table tells how many shells there will be. Helium (n = 1), neon (n = 2), argon (n = 3), etc. Note that the shells will have different numbers, as described by the table above; for example, argon will contain the , , and subshells, for that total of 3.
Angular Momentum Quantum Number (l)
[edit | edit source]Also known as azimuthal quantum number. Determines the subshell the electron is in. Each subshell has a unique shape and a letter name. The s orbital is shaped like a sphere and occurs when l = 0. The p orbitals (there are three) are shaped like teardrops and occur when l = 1. The d orbitals (there are five) occur when l = 2. The f orbitals (there are seven) occur when l = 3. (By the way, when l = 4, the orbitals are "g orbitals", but they (and the l = 5 "h orbitals") can safely be ignored in general chemistry.). The numbers of the subshells in each shell can be calculated using the principal quantum number like so. For example, in the shell, the subshells are an subshell, and 3 subshells. You will learn how to determine the number of orbitals for each subshells in the next section.
This number also gives information as to what the angular node of an orbital is. A node is defined as a point on a standing wave where the wave has minimal amplitude. When applied to chemistry this is the point of zero-displacement and thus where no electrons are found. In turn angular node means the planar or conical surface in which no electrons are found or where there is no electron density. The models shown on this page show the most simple representations of these orbitals and their nodes. More accurate, but more complex depictions are not necessary for the scope of this book.
Here are pictures of the orbitals. Keep in mind that they do not show the actual path of the electrons, due to the Heisenberg Uncertainty Principle. Instead, they show the volume where the electron is most likely to occur, i.e. the probability amplitude is largest. The two colors represent two signs (phases) of the wave function (the choice is arbitrary). Each of the depicted orbitals is a superposition of two opposite m quantum numbers (see below).
| ml | 0 | -1 and 1 | -2 and 2 | -3 and 3 |
|---|---|---|---|---|
| S orbital → | 
|
|||
| P orbitals → | 
|
 
|
||
| D orbitals → | 
|
 
|
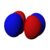 
|
|
| F orbitals → | 
|
 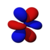
|
 
|
 
|
Magnetic Quantum Number (ml)
[edit | edit source]| ml | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| S orbital → | 
|
||||||
| P orbitals → | 
|

|

|
||||
| D orbitals → | 
|

|

|

|

|
||
| F orbitals → | 
|

|

|

|

|

|

|
Magnetic quantum number determines the orbital in which the electron lies. The number of orbitals in each subshell can be calculated like so: . ml determines how rapidly the complex phase increases around the z-axis. Without magnetic field, these orbitals all have the same energy, they are degenerate and can be combined into different shapes and spatial orientations. The orbitals in a subshell with degeneracy are called degenerate orbitals. This simply means that the orbitals in each p subshell all have the same energy level. The difference in shapes as well as orientation of higher subshells is not important during general chemistry, and the orbitals in the same higher subshells are still degenerate regardless of shape differences.
Spin Quantum Number (ms)
[edit | edit source]Does not determines the spin on the electron. +½ corresponds to the up arrow in an electron configuration box. If there is only one electron in an orbital (one arrow in one box), then it is always considered +½. The second arrow, or down arrow, is considered -½. Every orbital can contain one "spin up" electron, and one "spin down" electron.
Some Examples
[edit | edit source]Let's examine the quantum numbers of electrons from a magnesium atom, 12Mg. Remember that each list of numbers corresponds to (n, l, ml, ms).
| Two s electrons: | (1, 0, 0, +½) | (1, 0, 0, -½) | ||||
| Two s electrons: | (2, 0, 0, +½) | (2, 0, 0, -½) | ||||
| Six p electrons: | (2, 1, -1, +½) | (2, 1, -1, -½) | (2, 1, 0, +½) | (2, 1, 0, -½) | (2, 1, 1, +½) | (2, 1, 1, -½) |
| Two s electrons: | (3, 0, 0, +½) | (3, 0, 0, -½) |
The Periodic Table
[edit | edit source]Notice a pattern on the periodic table. Different areas, or blocks, have different types of electrons. The two columns on the left make the s-block. The six columns on the right make the p-block. The large area in the middle (transition metals) makes the d-block. The bottom portion makes the f-block (Lanthanides and Actinides). Each row introduces a new shell (aka energy level). Basically, the row tells you how many shells of electrons there will be, and the column tells you which subshells will occur (and which shells they occur in). The value of ml can be determined by some of the rules we will learn in the next chapter. The value of ms doesn't really matter as long as there are no repeating values in the same orbital.
To see the pattern better, take a look at this periodic table. |
















