General Chemistry/Shells and Orbitals
Electron shells
[edit | edit source]Each shell is subdivided into subshells, which are made up of orbitals, each of which has electrons with different angular momentum. Each orbital in a subshell has a characteristic shape, and is named by a letter. They are: s, p, d, and f. In a one-electron atom (e.g. H, He+, Li+2, etc.) the energy of each orbital within a particular shell is identical. However, when there are multiple electrons, they interact and split the orbitals into slightly different energies. The letters s, p, d and f specify the subshells (angular quantum number l) and the orbital is specified by the magnetic quantum number m. The angular and magnetic quantum numbers relate to the magnitude and direction of the electron's angular momentum, respectively. Within any particular subshell, the energy of the orbitals depends on the angular momentum of orbitals s, p, d, and f in order of lowest to highest energy.
This image shows the orbitals (along with hybrid orbitals for bonding and a sample electron configuration, explained later).

The s subshell
[edit | edit source]The simplest subshell in the atom is the 1s subshell. It has no radial or angular nodes: the 1s subshell is simply a sphere of electron density. A node is a point where the electron positional probability is zero. As with all subshell the number of radial nodes increases with the principle quantum number (i.e. the 2s orbital has one radial node, the 3s has two etc.). Because the angular momentum quantum number is 0, there is only one choice for the magnetic quantum number - there is only one s orbital per shell. The s orbital can hold two electrons, as long as they have different spin quantum numbers. S orbitals are involved in bonding.
The p subshell
[edit | edit source]Starting from the 2nd shell, there is a set of p subshell. The angular momentum quantum number of the electrons confined to p subshell is 1, so each orbital has one angular node. There are 3 choices for the magnetic quantum number, which indicates 3 differently oriented p subshell. Finally, each orbital can accommodate two electrons (with opposite spins), giving the p orbitals a total capacity of 6 electrons.
The orbital of p subshell all have two lobes of electron density pointing along each of the axes. Each one is symmetrical along its axis. The notation for the orbitals of p subshell indicate which axis it points down, i.e. px points along the x axis, py on the y axis and pz up and down the z axis. Note that although pz corresponds to the ml = 0 orbital, px and py are actually mixtures of ml = -1 and ml = 1 orbitals. The p orbitals are degenerate — they all have the same energy. P orbitals are very often involved in bonding.
| 2px | 2py | 2pz |
|---|---|---|

|

|

|
The d subshell
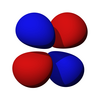
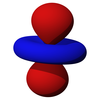
[edit | edit source]The first set of d orbitals is the 3d set. The angular momentum quantum number is 2, so each orbital has two angular nodes. There are 5 choices for the magnetic quantum number, which gives rise to 5 different d orbitals. Each orbital can hold two electrons (with opposite spins), giving the d orbitals a total capacity of 10 electrons.
Note that all the d orbitals have four lobes of electron density, except for the dz2 orbital, which has two opposing lobes and a doughnut of electron density around the middle. The d orbitals can be further subdivided into two smaller sets. The dx2-y2 and dz2 all point directly along the x, y, and z axes. They form an eg set. On the other hand, the lobes of the dxy, dxz and dyz all line up in the quadrants, with no electron density on the axes. These three orbitals form the t2g set. In most cases, the d orbitals are degenerate, but sometimes they can split, with the eg and t2g subsets having different energy. Crystal Field Theory predicts and accounts for this. D orbitals are sometimes involved in bonding, especially in inorganic chemistry.

|
|
|

|

|
The f subshell
[edit | edit source]The first set of f orbitals is the 4f subshell. There are 7 possible magnetic quantum numbers, so there are 7 f orbitals. Their shapes are fairly complicated, and they rarely come up when studying chemistry. There are 14 f electrons because each orbital can hold two electrons (with opposite spins).

|

|

|

|

|

|

|



