How to find the angles of the parametric external rays that land on the p/q root point on the boundary of Mandelbrot set's main cardioid ( period 1 component) ?

Images

wakes
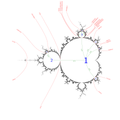
Wakes near the period 1 continent
Wakes_along_the_main_antenna
wakes up to period 10

rotation, winding numbers and regular star polygons

irreducible fraction

First check of p/q is irreducible

/*
https://stackoverflow.com/questions/19738919/gcd-function-for-c
The GCD function uses Euclid's Algorithm. 
It computes A mod B, then swaps A and B with an XOR swap.
*/
int gcd(int a, int b)
{
    int temp;
    while (b != 0)
    {
        temp = a % b;

        a = b;
        b = temp;
    }
    return a;
}


/*
 n/d -> n_new/d_new
 
*/

int give_reduced_fraction(const int n, const int d, int * n_new, int *d_new){


	int divisor = gcd(n,d);
	if (divisor != 1) {
		*n_new = n / divisor;
		*d_new = d / divisor;}
		
		else {
			*n_new = n;
         		*d_new = d;
		}
	return 0;
}

Wake and limb

Wake is the region of parameter plane enclosed by two external rays landing on the same root point on the boundary of main cardioid (period 1 hyperbolic component).

p/q-limb is a part of Mandelbrot set contained inside p/q-wake

Limb:

start from the root point
end with tip point

External angles of p/q-wake:

have period q under doubling map. It is the same as period of it's landing point ( c = root point ) and parent hyperbolic component
length of periodic part of binary expansion is q
preperiod under doubling map is zero

Points of of p/q-wake:

Roots are landing points of parameter rays with periodic angles
Misiurewicz points have preperiodic external angles

The size of the p/q limb^[1] is ${\frac {1}{2^{q}-1}}$

The p/q bulb can be recognized by locating the smallest spoke ( branch) in the antenna and determining its relative location to the main spoke.

wake, principal Misiurewicz point and dendrite Julia set

Notes from demo 3 (external rays) page 9/12 from program mandel by Wolf Jung

The parameter rays with the angles 1/7 and 2/7 land at the root of a period-3 component, which is of satellite type with rotation number 1/3.

For all parameters c in the wake between the rays

for c in the 1/3-limb of the Mandelbrot set,
- for the principle Misiurewicz point of the wake

the dynamic rays with the angles 1/7, 2/7, and 4/7:

land together at the repelling fixed point $z=\alpha _{c}$
the critical value z = c is between the first two rays.

We shall compute the external angles of certain preimages of αc under fc(z). Note that an angle θ has two preimages under doubling modulo 1, θ/2 and (θ+1)/2.

$z=-\alpha _{c}$ is the only preimage of $z=\alpha _{c}$ different from the fixed point itself. The angle 1/7 has the preimages (1/7)/2 = 1/14 and (1/7 + 1)/2 = 4/7. The latter angle belongs to $z=\alpha _{c}$ , so 1/14 is an external angle of $z=-\alpha _{c}$ . In the same way, the other angles 9/14 and 11/14 are obtained. The rays are drawn blue. Move z to that preimage of $z=-\alpha _{c}$ between the rays for 2/7 and 4/7. The angle 1/14 has the preimages (1/14)/2 = 1/28 and (1/14 + 1)/2 = 15/28. Only the latter angle is in the chosen interval. The other two external angles of z are 9/28 and 11/28. The rays are drawn magenta. Now z is the preimage between the rays for 1/7 and 2/7. By taking preimages in this interval, the external angles 9/56, 11/56, and 15/56 are obtained. The rays are drawn red. Rays with preperiodic angles, i.e., even denominators, land at preperiodic points in the dynamic plane, or at Misiurewicz points in the parameter plane. For these parameters, the critcal value is preperiodic under the iteration of fc(z).

How to compute angles of the wake ?

algorithm from demo 4 page 1 of program Mandel: When the parameter c of a center is given, read off the angles or the Hubbard tree.
- draw the filled Julia set Kc ( the parameter c is the center of this hyperbolic component)
- locate $\mp \beta _{c}$ ( the angles 0 and 1/2 are landing at the fixed point $\beta _{c}$ and at its preimage $-\beta _{c}$ ) and
- locate the two accesses to the 5-periodic point
- Follow the orbit of these accesses and note the digits 0 or 1 according to the upper or lower sides of the Julia set. Dynamic rays in the upper part between these two rays have an angle between 0 and 1/2, the first binary digit is 0. Angles in the lower part are between 1/2 and 1, with first digit 1.
- You may need to magnify subsets carefully. Or use the inverse spider algorithm.
Angles of the wake from program mandel - code
Combinatorial algorithm = Devaney's method

The paritition of dynamic plane: ^[2]

the partition used in the definition of the kneading sequence: divide open unit disc into two parts: $\theta /2$ $\theta /2$ and $(\theta +1)/2$ $(\theta +1)/2$ (the two inverse images of $\theta$ under angle doubling);
- the open part containing the angle 0 is labeled 0
- the other open part is labeled 1
- the boundary gets the label ⋆

Combinatorial algorithm = Devaney's method

Devaney's method^[3] for finding external angles of primary buds^[4]^[5]

Steps :

start with rational rotation angle,
orbit of rotation angle under circle map
translation of orbit into itinerary
conversion of itinerary into binary expansion with repeating binary fraction
conversion of binary expansion to binary fraction
conversion to decimal fraction

Input : rational rotation angle

Outpout : external angle ( decimal or binary fraction )

The code

C++

Here is C++ code from the program Mandel by Wolf Jung :

// mndcombi.cpp  by Wolf Jung (C) 2007-2015, part of Mandel 5.13, 
qulonglong mndAngle::wake(int k, int r, qulonglong &n)
{  if (k <= 0 || k >= r || r > 64) return 0LL;
   qulonglong d = 1LL; 
   int j, s = 0; 
   n = 1LL;

   for (j = 1; j < r; j++)
   {  s -= k; if (s < 0) s += r; if (!s) return 0LL;
      if (s > r - k) n += d << j;
   }
   //
   d <<= (r - 1); d--; d <<= 1; d++; //2^r - 1 for r <= 64
   return d;
}

C GMP and MPFR

/*

------- Git -----------------
cd existing_folder
git init
git remote add origin git@gitlab.com:adammajewski/wake_gmp.git
git add .
git commit -m ""
git push -u origin master
-------------------------------

?? http://stackoverflow.com/questions/2380415/how-to-cut-a-mpz-t-into-two-parts-using-gmp-lib-on-c

   
   to compile from console:
   gcc w.c -lgmp -lmpfr -Wall

    to run from console :

   ./a.out

   tested on Ubuntu 14.04 LTS

uiIADenominator = 89 
Using MPFR-3.1.2-p3 with GMP-5.1.3 with precision = 200 bits 
internal angle = 34/89
first external angle : 
period = denominator of internal angle = 89
external angle as a decimal fraction = 179622968672387565806504265/618970019642690137449562111 = 179622968672387565806504265 /( 2^89 - 1) 
External Angle as a floating point decimal number =  2.9019655713870868535821260055542440298749779423213948304299730531995503353103626302473331181359966368582651105245850405837027542373052381532777325121338632071561064451614697645709384232759475708007812e-1
external angle as a binary rational (string) : 1001010010010100101001001010010010100101001001010010100100101001001010010100100101001001/11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 
external angle as a binary floating number in exponential form =0.10010100100101001010010010100100101001010010010100101001001010010010100101001001010010010100101001001010010100100101001001010010100100101001010010010100100101001010010010100100101001010010010100101001*2^-1
external angle as a binary floating number in periodic form =0.(01001010010010100101001001010010010100101001001010010100100101001001010010100100101001001)

                                                             .(01001010010010100101001001010010010100101001001010010100100101001001010010100100101001001)

*/

#include <stdlib.h> // malloc
#include <stdio.h>
#include <gmp.h>  // for rational numbers 
#include <mpfr.h> // for floating point mumbers

 // rotation map 
//the number  n  is always increased by n0 modulo d

// input :  op = n/d ( rational number ) and n0 ( integer)
//  n = (n + n0 ) % d
// d = d
// output = rop = n/d
void mpq_rotation(mpq_t rop, const mpq_t op, const mpz_t n0)
{
  
  mpz_t n; // numerator
  mpz_t d; // denominator
  mpz_inits( n, d, NULL);

 
  //  
  mpq_get_num (n, op); // 
  mpq_get_den (d, op);
  
 
  // n = (n + n0 ) % d
  mpz_add(n, n, n0); 
  mpz_mod( n, n, d);
  
      
  // output
  mpq_set_num(rop, n);
  mpq_set_den(rop, d);
    
  mpz_clears( n, d, NULL);

}

void mpq_wake(mpq_t rop, mpq_t op)
{
   
  // arbitrary precision variables from GMP library
   mpz_t  n0 ; // numerator of q
   mpz_t  nc;
   mpz_t  n;
   mpz_t  d ; // denominator of q
   mpz_t  m; // 2^i

   mpz_t  num ; // numerator of rop
   mpz_t  den ; // denominator of rop
   long long int i;
   unsigned long int base = 2;
   unsigned long int id;
   int cmp;

   mpz_inits(n, n0,nc,d,num,den,m, NULL);

   mpq_get_num(n0,op);
   mpq_get_den(d,op);
   id = mpz_get_ui(d);
   //  if (n <= 0 || n >= d ) error !!!! bad input
   mpz_sub(nc, d, n0); // nc = d - n0
   mpz_set(n, n0);   
   mpz_set_ui(num, 0);

   // rop  
    // num = numerator(rop)
    
   
   // denominator = den(rop) = (2^i) -1 
   mpz_ui_pow_ui(den, base, id) ;  // den = base^id
   mpz_sub_ui(den, den, 1);   // den = den-1
   
  // numerator   
     for (i=0; i<id ; i++){  
       
       mpz_set_ui(m, 0);
       cmp = mpz_cmp(n,nc);// Compare op1 and op2. Return a positive value if op1 > op2, zero if op1 = op2, or a negative value if op1 < op2.
       if ( cmp>0 ) {
          mpz_ui_pow_ui(m, 2, id-i-1); // m = 2^(id-i   )
          mpz_add(num, num, m); // num = num + m
          if (mpz_cmp(num, den) >0) mpz_mod( num, num, den); // num = num % d ; if num==d gives 0
          //gmp_printf("s = 1");

           }
        // else gmp_printf("s = 0");
       //gmp_printf (" i = %ld internal angle = %Zd / %Zd ea = %Zd / %Zd ; m = %Zd \n", i, n, d, num, den, m);

        // n = (n + n0 ) % d = rotation 
       mpz_add(n, n, n0); 
       if (mpz_cmp(n, d)>0) mpz_mod( n, n, d);
       //
       
          
        // 
      }

    
   // rop = external angle 
   mpq_set_num(rop,num);
   mpq_set_den(rop,den);
   mpq_canonicalize (rop); // It is the responsibility of the user to canonicalize the assigned variable before any arithmetic operations are performed on that variable.

    
   // clear memory
   mpz_clears(n, n0, nc, d, num,den, m, NULL);

}

/*

http://stackoverflow.com/questions/9895216/remove-character-from-string-in-c

"The idea is to keep a separate read and write pointers (pr for reading and pw for writing), 
always advance the reading pointer, and advance the writing pointer only when it's not pointing to a given character."

modified

 remove first length2rmv chars and after that take only length2stay chars from input string
 output = input string 
*/
void extract_str(char* str, unsigned int length2rmv, unsigned long int length2stay) {
    // separate read and write pointers 
    char *pr = str; // read pointer
    char *pw = str; // write pointer
    int i =0; // index

    while (*pr) {
        if (i>length2rmv-1 && i <length2rmv+length2stay)
          pw += 1; // advance the writing pointer only when 
        pr += 1;  // always advance the reading pointer
        *pw = *pr;    
        i +=1;
    }
    *pw = '\0';
}

int main ()
{	

	

         // notation : 
        //number type : s = string ; q = rational ; z = integer, f = floating point
        // base : b = binary ; d = decimal

        
        char *sqdInternalAngle = "13/34";
        mpq_t qdInternalAngle;   // internal angle = rational number q = n/d
        mpz_t den;  
        unsigned long int uiIADenominator;
        
       
        mpq_t  qdExternalAngle;   // rational number q = n/d
        char  *sqbExternalAngle;
        mpfr_t  fdExternalAngle ;  // 
        char  *sfbExternalAngle; // 
        
        mp_exp_t exponent ; // holds the exponent for the result string
        mpz_t zdEANumerator;
        mpz_t zdEADenominator;
        mpfr_t EANumerator;
        mpfr_t EADenominator;
        mpfr_prec_t p = 200; // in bits , should be > denominator of internal angle

         mpfr_set_default_prec (p); // but previously initialized variables are unaffected.
        //mpfr_set_default_prec (precision);

        // init variables 
        //mpf_init(fdExternalAngle);
        mpz_inits(den, zdEANumerator,zdEADenominator, NULL);
        mpq_inits (qdExternalAngle, qdInternalAngle, NULL); //
        mpfr_inits(fdExternalAngle, EANumerator, EADenominator, NULL);

        // set variables
        mpq_set_str(qdInternalAngle, sqdInternalAngle, 10); // string is an internal angle
        mpq_canonicalize (qdInternalAngle); // It is the responsibility of the user to canonicalize the assigned variable before any arithmetic operations are performed on that variable.
        mpq_get_den(den,qdInternalAngle); 
        uiIADenominator = mpz_get_ui(den);
        printf("uiIADenominator = %lu \n", uiIADenominator);

        if ( p < uiIADenominator) printf("increase precision !!!!\n");         
        mpfr_printf("Using MPFR-%s with GMP-%s with precision = %u bits \n", mpfr_version, gmp_version, (unsigned int) p);

        //        
        mpq_wake(qdExternalAngle, qdInternalAngle); // internal -> external

        mpq_get_num(zdEANumerator  ,qdExternalAngle);
        mpq_get_den(zdEADenominator,qdExternalAngle); 
        // conversions
        mpfr_set_z (EANumerator,   zdEANumerator,   GMP_RNDN);
        mpfr_set_z (EADenominator, zdEADenominator, GMP_RNDN);

        sqbExternalAngle = mpq_get_str (NULL, 2, qdExternalAngle); // rational number = fraction : from decimal to binary
        
        mpfr_div (fdExternalAngle, EANumerator, EADenominator, GMP_RNDN);

        sfbExternalAngle = (char*)malloc((sizeof(char) * uiIADenominator*2*4) + 3);
        // mpfr_get_str (char *str, mpfr_exp_t *expptr, int b, size_t n, mpfr_t op, mpfr_rnd_t rnd)
        if (sfbExternalAngle==NULL ) {printf("sfbExternalAngle error \n"); return 1;}
        mpfr_get_str(sfbExternalAngle, &exponent, 2,200, fdExternalAngle, GMP_RNDN);

        // print
        gmp_printf ("internal angle = %Qd\n", qdInternalAngle); // 
        printf("first external angle : \n");
        gmp_printf ("period = denominator of internal angle = %Zd\n", den); //

        gmp_printf ("external angle as a decimal fraction = %Qd = %Zd /( 2^%Zd - 1) \n", qdExternalAngle, zdEANumerator, den); // 
        printf ("External Angle as a floating point decimal number =  ");
        mpfr_out_str (stdout, 10, p, fdExternalAngle, MPFR_RNDD); putchar ('\n');
        gmp_printf ("external angle as a binary rational (string) : %s \n", sqbExternalAngle); // 
        
        printf ("external angle as a binary floating number in exponential form =0.%s*%d^%ld\n", sfbExternalAngle, 2, exponent); 
        extract_str(sfbExternalAngle,  uiIADenominator+exponent, uiIADenominator); 
        printf ("external angle as a binary floating number in periodic form =0.(%s)\n", sfbExternalAngle);

        // clear memory
        //mpf_clear(fdExternalAngle);
        mpq_clears(qdExternalAngle, qdInternalAngle, NULL);
        mpz_clears(den, zdEANumerator, zdEADenominator, NULL);
        mpfr_clears(fdExternalAngle, EANumerator, EADenominator, NULL);
        free(sfbExternalAngle);

        return 0;
}

haskell

Code and description by Claude Heiland-Allen^[6]

mandelbrot web interface

Primary Bulb The child bulb of the period $1$ cardioid at internal angle ${\frac {p}{q}}$ has external angles:

[(.{\overline {b_{0}b_{1}\ldots b_{q-3}01}},.{\overline {b_{0}b_{1}\ldots b_{q-3}10}})]

where

[b_{0}b_{1}\ldots =\operatorname {map} \left(\in \left(1-{\frac {p}{q}},1\right)\right)\circ \operatorname {iterate} \left(+{\frac {p}{q}}\right)\${\frac {p}{q}}]

import Data.Fixed (mod')
import Data.List (genericTake)
import Data.Ratio (denominator)

type InternalAngle = Rational
type ExternalAngle = ([Bool], [Bool])

primaryBulb
  :: InternalAngle
  -> (ExternalAngle, ExternalAngle)
primaryBulb pq
  = ( ([], bs ++ [False, True])
    , ([], bs ++ [True, False])
    )
  where
    q = denominator pq
    bs
      = genericTake (q - 2)
      . map (\x -> 1 - pq < x && x < 1)
      . iterate (\x -> (x + pq) `mod'` 1)
      $ pq

Examples

One can check the results with

1/2

The 1/2-wake of the main cardioid is bounded by the parameter rays with the angles:

1/3 = p01 = 0.(01)
2/3 = p10 = 0.(10)

The 1/2-wake of the main cardioid is bounded by the parameter rays with the angles 1/3  or  p01  and 2/3  or  p10 .

The angle  1/3  or  p01 has  preperiod = 0  and  period = 2. 
The conjugate angle is  2/3  or  p10 . 
The kneading sequence is  A*  and the internal address is  1-2 .
The corresponding parameter rays land at the root of a satellite component of period 2. It bifurcates from period 1.

Important points

root point between period 1 and 2 = c = -0.75 = -3/4 = birurcation point for internal angle 1/2. Landing point of 2 external rays 1/3 and 2/3
center of period 2 components c = -1
tip of main antenna c = -2 = $M_{1,1}$ . It is landing point of externa ray for angle $0.01={\frac {1}{2}}=0.5$

1/3

Orbit of rational angle 3/7 ( and position in subintervals):

 1 / 3  = 0 
 2 / 3  = 0 
 0 / 3  = 1

so intinerary = 001

first external angle  = 001 = 1 / 7

The 1/3-wake of the main cardioid is bounded by the parameter rays with the angles

1/7 = p001 = 0.(001)
2/7 = p010 = 0.(010)

note that

1/7 = 0.(142857)= 0.1428571428571428571428571428571428571428571428571428571428571428571428571428571428571428571428571428571428571428...

but decimal expansion is not important here. Only decimal ratio and binary floating point is important

${\begin{cases}0.(s_{-})=0.(001)_{2}={\frac {1}{7}}=0.(142857)_{10}=wake\\0.(s_{+})=0.(010)_{2}={\frac {2}{7}}=0.(285714)=wake\\\end{cases}}$

1/4

The 1/4-wake of the main cardioid is bounded by the parameter rays with the angles

1/15 or p0001 or $0.(0001)$
2/15 or p0010 or $0.(0010)$

n/5

There are 4 period 5 wakes:

1/5
2/5
3/5
4/5

The 1/5-wake of the main cardioid is bounded by the parameter rays with the angles :

1/31 = p00001 = 0.(00001)
2/31 = p00010 = 0.(00010)

The 4/5-wake of the main cardioid is bounded by the parameter rays with the angles

29/31 = p11101 = 0.(11101)
30/31 = p11110 = 0.(11110)

3/7

Divide interval ( circle):

 $I={\big (}0,1{\big ]}$

into 2 subintervals ( lower partition) :

 $I_{0}={\big (}{\tfrac {0}{7}},{\tfrac {4}{7}}{\big ]}$

 $I_{1}={\big (}{\tfrac {4}{7}},{\tfrac {7}{7}}{\big ]}$

Orbit of rational angle 3/7 ( and position in subintervals):

So itinerary is :

  $0101001$

One can convert it to number :

$0101001\to 0.(0101001)_{2}={\frac {0101001}{1111111}}_{2}={\frac {41}{127}}_{10}$

The 3/7-wake of the main cardioid is bounded by the parameter rays with the angles

41/127 = p0101001 = 0.(0101001)
42/127 = p0101010 = 0.(0101010)

root point :

 c = -0.606356884415893  +0.412399740175787 i

Orbit of 41/127 under doubling map modulo 1 computed with this program ( exponent = 7 and mpz_init_set_ui(n, 41); :

5/11

ghci
GHCi, version 8.10.7: https://www.haskell.org/ghc/  :? for help
Prelude> :l bh.hs
[1 of 1] Compiling Main             ( bh.hs, interpreted )
Ok, one module loaded.
*Main> :main 5 11
internal angle p/q = 5 / 11
internal angle in lowest terms = 
5 % 11
rays of the bulb:
(01010101001) = 681 % 2047
(01010101010) = 682 % 2047

The 5/11-wake of the main cardioid is bounded by the parameter rays with the angles:

681/2047 = p01010101001 = 0.(01010101001)
682/2047 = p01010101010 = 0.(01010101010)

Center of period 11: c = -0.697838195122425 +0.279304134101366 i root point ( bond): c = -0.690059870015044 +0.276026482784614 i

Angled internal address: $1\xrightarrow {5/11} 11$

n/17

The 1/17-wake of the main cardioid is bounded by the parameter rays with the angles

1/131071 = p00000000000000001 = 0.(00000000000000001)
2/131071 = p00000000000000010 = .(00000000000000010)

10/21

Parameter plane:

root point c = -0.733308614559099 +0.148209926690813 i
The 10/21-wake of the main cardioid is bounded by the parameter rays with the angles:
- 699049/2097151 or p010101010101010101001
- 699050/2097151 or p010101010101010101010

Dynamical plane

external rays of the wake do not bound critical sector
- 699049/2097151 or p010101010101010101001
- 699050/2097151 or p010101010101010101010
alpha fixed point ( period 1) z = -0.494415413112564 +0.074521133088087i

1/25

uiIADenominator = 25 
Using MPFR-3.1.5 with GMP-6.1.1 with precision = 200 bits 
internal angle = 1/25
first external angle : 
period = denominator of internal angle = 25
external angle as a decimal fraction = 1/33554431 = 1 /( 2^25 - 1) 
External Angle as a floating point decimal number =  2.9802323275873758669905622896719661257256902970579355078320375103410059138021557873907862143745145987726127630324761942815747600646073471636075786857847163330961076713939572483194617724677755177253857e-8
external angle as a binary rational (string) : 1/1111111111111111111111111 
external angle as a binary floating number in exponential form =0.10000000000000000000000001000000000000000000000000100000000000000000000000010000000000000000000000001000000000000000000000000100000000000000000000000010000000000000000000000001000000000000000000000001*2^-24
external angle as a binary floating number in periodic form =0.(0000000000000000000000001)

So 1/25-wake of the main cardioid is bounded by the parameter rays with the angles :

0.0000000298 = 1/33554431 = 1 /( 2^25 - 1) = 0.(0000000000000000000000001)
0,0000000596 = 2/33554431 = 2 /( 2^25 - 1) = 0.(0000000000000000000000010)

One can check it with Mandel

The angle  1/33554431  or  p0000000000000000000000001
has  preperiod = 0  and  period = 25.
The conjugate angle is  2/33554431  or  p0000000000000000000000010 .
The kneading sequence is  AAAAAAAAAAAAAAAAAAAAAAAA*  and
the internal address is  1-25 .
The corresponding parameter rays are landing at the root of a satellite component of period 25.
It is bifurcating from period 1.
Do you want to draw the rays and to shift c
to the corresponding center?

The center is :

 c = 0.265278321904606  +0.003712059989878 i    period = 25

12/25

wake 12/25

root c = -0.738203140939397 +0.124839088573366 i
The 12/25-wake of the main cardioid is bounded by the parameter rays with the angles
- 11184809/33554431 or p0101010101010101010101001 and
- 11184810/33554431 or p0101010101010101010101010 .
the center of the satellite component c = -0.739829393511579 +0.125072144080321 i period = 25

1/31

The 1/31-wake of the main cardioid

is bounded by the parameter rays with the angles:
- 1/2147483647 = p0000000000000000000000000000001 = 0.(0000000000000000000000000000001)
- 2/2147483647 = p0000000000000000000000000000010 = 0.(0000000000000000000000000000010)
root point : c = 0.260025517721190 +0.002060296266000 i
center c = 0.260025517721190 +0.002060296266000 i
principal Misiurewicz point c = 0.259995759918769 +0.001610271381965*i
- has preperiod = 31 , period = 1
- is a landing point for 31 external rays
  - 2147483649/4611686016279904256 = 0000000000000000000000000000001p0000000000000000000000000000010 = .0000000000000000000000000000001(0000000000000000000000000000010)
the biggest baby Mandelbrot set has the kneading sequence AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB* corresponds to the internal address 1-31-32 . The period is 32. The smallest angles are 3/4294967295 = 0.(00000000000000000000000000000011) and 4/4294967295 = 0.(00000000000000000000000000000100)

On the dynamical plane :

The angle

13/34

The 13/34-wake of the main cardioid is bounded by the parameter rays with the angles

4985538889/17179869183 = p0100101001001010010100100101001001 = 0.(0100101001001010010100100101001001)
4985538890/17179869183 = p0100101001001010010100100101001010 = 0.(0100101001001010010100100101001010)

 s = 0 i = 0 internal angle = 13 / 34 ea = 0 / 17179869183 ; m = 0 
s = 1 i = 1 internal angle = 26 / 34 ea = 4294967296 / 17179869183 ; m = 4294967296 
s = 0 i = 2 internal angle = 5 / 34 ea = 4294967296 / 17179869183 ; m = 0 
s = 0 i = 3 internal angle = 18 / 34 ea = 4294967296 / 17179869183 ; m = 0 
s = 1 i = 4 internal angle = 31 / 34 ea = 4831838208 / 17179869183 ; m = 536870912 
s = 0 i = 5 internal angle = 10 / 34 ea = 4831838208 / 17179869183 ; m = 0 
s = 1 i = 6 internal angle = 23 / 34 ea = 4966055936 / 17179869183 ; m = 134217728 
s = 0 i = 7 internal angle = 2 / 34 ea = 4966055936 / 17179869183 ; m = 0 
s = 0 i = 8 internal angle = 15 / 34 ea = 4966055936 / 17179869183 ; m = 0 
s = 1 i = 9 internal angle = 28 / 34 ea = 4982833152 / 17179869183 ; m = 16777216 
s = 0 i = 10 internal angle = 7 / 34 ea = 4982833152 / 17179869183 ; m = 0 
s = 0 i = 11 internal angle = 20 / 34 ea = 4982833152 / 17179869183 ; m = 0 
s = 1 i = 12 internal angle = 33 / 34 ea = 4984930304 / 17179869183 ; m = 2097152 
s = 0 i = 13 internal angle = 12 / 34 ea = 4984930304 / 17179869183 ; m = 0 
s = 1 i = 14 internal angle = 25 / 34 ea = 4985454592 / 17179869183 ; m = 524288 
s = 0 i = 15 internal angle = 4 / 34 ea = 4985454592 / 17179869183 ; m = 0 
s = 0 i = 16 internal angle = 17 / 34 ea = 4985454592 / 17179869183 ; m = 0 
s = 1 i = 17 internal angle = 30 / 34 ea = 4985520128 / 17179869183 ; m = 65536 
s = 0 i = 18 internal angle = 9 / 34 ea = 4985520128 / 17179869183 ; m = 0 
s = 1 i = 19 internal angle = 22 / 34 ea = 4985536512 / 17179869183 ; m = 16384 
s = 0 i = 20 internal angle = 1 / 34 ea = 4985536512 / 17179869183 ; m = 0 
s = 0 i = 21 internal angle = 14 / 34 ea = 4985536512 / 17179869183 ; m = 0 
s = 1 i = 22 internal angle = 27 / 34 ea = 4985538560 / 17179869183 ; m = 2048 
s = 0 i = 23 internal angle = 6 / 34 ea = 4985538560 / 17179869183 ; m = 0 
s = 0 i = 24 internal angle = 19 / 34 ea = 4985538560 / 17179869183 ; m = 0 
s = 1 i = 25 internal angle = 32 / 34 ea = 4985538816 / 17179869183 ; m = 256 
s = 0 i = 26 internal angle = 11 / 34 ea = 4985538816 / 17179869183 ; m = 0 
s = 1 i = 27 internal angle = 24 / 34 ea = 4985538880 / 17179869183 ; m = 64 
s = 0 i = 28 internal angle = 3 / 34 ea = 4985538880 / 17179869183 ; m = 0 
s = 0 i = 29 internal angle = 16 / 34 ea = 4985538880 / 17179869183 ; m = 0 
s = 1 i = 30 internal angle = 29 / 34 ea = 4985538888 / 17179869183 ; m = 8 
s = 0 i = 31 internal angle = 8 / 34 ea = 4985538888 / 17179869183 ; m = 0 
s = 0 i = 32 internal angle = 21 / 34 ea = 4985538888 / 17179869183 ; m = 0 
s = 1 i = 33 internal angle = 34 / 34 ea = 4985538889 / 17179869183 ; m = 1 
internal angle = 13/34
period = denominator of internal angle = 34
external angle as a decimal fraction = 4985538889/17179869183 = 4985538889 /( 2^34 - 1) 
external angle as a binary rational (string) : 100101001001010010100100101001001/1111111111111111111111111111111111 
external angle as a binary floating number in exponential form =0.1001010010010100101001001010010010100101001001010010100100101001*2^-1
external angle as a binary floating number in periodic form =0.(0100101001001010010100100101001)

34/89

Using GMP-5.1.3 with precision = 256 bits 
internal angle = 34/89
period = denominator of internal angle = 89
external angle as a decimal fraction = 179622968672387565806504265/618970019642690137449562111
external angle as a binary rational (string) : 1001010010010100101001001010010010100101001001010010100100101001001010010100100101001001/11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 
external angle as a binary floating number in exponential form =0.10010100100101001010010010100100101001010010010100101001001010010010100101001001010010010100101001001010010100100101001001010010100100101001010010010100100101001010010010100100101001010010010100101001001010010010100101001001010010100100101001001010010100101*2^-1
external angle as a binary floating number in periodic form =0.(01001010010010100101001001010010010100101001001010010100100101001001010010100100101001001)

1/128

uiIADenominator = 128 
Using MPFR-4.0.2 with GMP-6.2.0 with precision = 200 bits 
internal angle = 1/128
first external angle : 
period = denominator of internal angle = 128
external angle as a decimal fraction = 1/340282366920938463463374607431768211455 = 1 /( 2^128 - 1) 
External Angle as a floating point decimal number =  2.9387358770557187699218413430556141945553000604853132483972656175588435482079339324933425313850237034701685918031624270579715075034722882265605472939461496635969950989468319466936530037770580747746862e-39
external angle as a binary rational (string) : 1/11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 
external angle as a binary floating number in exponential form =0.10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000100000000000000000000000000000000000000000000000000000000000000000000000*2^-127
external angle as a binary floating number in periodic form =0.(00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001)

89/268


Using GMP-5.1.3 with precision = 320 bits 
internal angle = 89/268
period = denominator of internal angle = 268
external angle as a decimal fraction = 67754913930863876636420964942226524366713408170066250043659752013773168429311121/474284397516047136454946754595585670566993857190463750305618264096412179005177855
external angle as a binary rational (string) : 0010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010001
/1111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 
external angle as a binary floating number in exponential form =0.10010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010001
001001001001001001001001001001001001001001001001001001*2^-2
external angle as a binary floating number in periodic form =
0.(0010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010010001)

G Pastor gave an example of external rays for which the resolution of the IEEE 754 is not sufficient ^[7]:

$\theta _{268}^{-}=0.((001)^{88}0001)_{2}={\frac {67754913930863876636420964942226524366713408170066250043659752013773168429311121}{474284397516047136454946754595585670566993857190463750305618264096412179005177855}}$

$\theta _{268}^{+}=0.((001)^{88}0010)_{2}={\frac {67754913930863876636420964942226524366713408170066250043659752013773168429311122}{474284397516047136454946754595585670566993857190463750305618264096412179005177855}}$

lists of roots

References

Bifurcation in Complex Quadrat ic Polynomial and Some Folk Theorems Involving the Geometry of Bulbs of the Mandelbrot Set by Monzu Ara Begum

[1] The Mandelbrot Set and the Farey Tree. American Mathematical Monthly 106 (1999), 289-302.

[2] Rational parameter rays of the Mandelbrot set by Dierk Schleicher

[3] The Mandelbrot Set and The Farey Tree by Robert L. Devaney

[4] External angles in the Mandelbrot set: the work of Douady and Hubbard by Douglas C. Ravenel

[5] Complex number and the Mandelbrot set by Dusa McDuff and Melkana Brakalova

[6] -primary-bulb by Claude Heiland-Allen

[7] A Method to Solve the Limitations in Drawing External Rays of the Mandelbrot Set M. Romera,1 G. Pastor, A. B. Orue,1 A. Martin, M.-F. Danca,and F. Montoya

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Fractals/Iterations in the complex plane/wake