Fractals/Iterations in the complex plane/Discrete Lagrangian Descriptors
Lagranian descriptor for continoust-time dynamical systems ( Lagrangian way to describe the flow)[1] [2] [3] [4] is a method for analyzing structure of the phase space. Here[5] [6] [7] [8] this method is extended to discrete dynamical systems: open maps in the complex plane.
Images
[edit | edit source]- period 1
-
Cauliflower_Julia_set - period 1 - parabolic case
-
parabolic case : field lines
- period 2
-
period 2 attracting case
-
Basilica Julia set - period 2 superattracting case
-
Fat Basilica: period 2 parabolic - field lines
- disconnected
-
Imploded cauliflower
Full source code is on the commons page ( click on the image)
key words
[edit | edit source]complex number
[edit | edit source]
complex map
[edit | edit source]
Riemann sphere
[edit | edit source]Point of the Riemann sphere
inverse stereographic projection
[edit | edit source]
inverse stereographic projection maps point of complex plane to point of Riemann sphere :
so
and
p-norm
[edit | edit source]The -norm (also called -norm) of vector is[9]
where
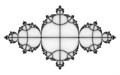
- number p is a real number . It is called a power. It affects the steepness of the gradient near singularities (fractal features like a Julia set)
p-norm is used to measure the distance between sequential iterations of the mapping f on the Riemann sphere
Discrete Lagrangian Descriptor = DLD
[edit | edit source]The simple idea is to compute the p-norm version of Lagrangian descriptors, not for the points on the complex plane, but for their projections on the Riemann sphere in the extended complex plane. ... in the complex mappings that we consider in this work, the functions that define the dynamics are not invertible, and therefore we will only keep the forward part of the definition.
DLD:
- is a scalar value
- accumulates the p-norm along the orbit (= has information about the history of the orbit) and therefore unveiles the structure of interior and exterior of Julia set
sum
[edit | edit source]summing is what the original paper does ( pauldelbrot)
where:
- N is a fixed number of iterations
- is any initial condition selected on a bounded subset D of the complex plane
- is a point of Riemann sphere:
Averaging
[edit | edit source]"averaging keeps the coloring stable if maxiters is changed but can lead to low variation over the image" pauldelbrot
Steps
[edit | edit source]For each point z of complex plane
- compute DLD ( scalar value)
- color is proportional to DLD
Substeps: To compute DLD of z :
- iterate point z under the map f = compute zn
- map each point zn from complex plane to the Riemann sphere ( Inverse Stereographic projection)
- for each zn compute summand
- ... ( to do )
Code
[edit | edit source]UltraFractal
[edit | edit source]DLD {
; Based on https://arxiv.org/pdf/2001.08937.pdf
; ucl file for UltraFractal by pauldelbrot
init:
float sum = 0.0
float lastx = 0.0
float lasty = 0.0
float lastz = 0.0
int i = 0
loop:
float d = |#z|
float dd = 1/(d + 1)
; Riemann sphere coordinates = (xx, yy,zz)
float xx = 2*real(#z)*dd
float yy = 2*imag(#z)*dd
float zz = (d - 1)*dd
:
IF (i > 0)
sum = sum + (xx - lastx)^@power + (yy - lasty)^@power + (zz - lastz)^@power
ENDIF
i = i + 1
lastx = xx
lasty = yy
lastz = zz
final:
#index = sum/(i - 1)
default:
title = "Discrete Langrangian Descriptors"
param power
caption = "Power"
default = 0.25
hint = "Affects the steepness of the gradient near singularities (fractal features like a Julia set)"
min = 0.0
endparam
}
" Here's the latest version I've been using in UF. It handles escaping points with no-bail formulae via the isInf/isNaN test (puts the Riemann sphere point at the north pole for those), allows averaging or summing (summing is what the original paper does, whereas averaging keeps the coloring stable if maxiters is changed but can lead to low variation over the image), and can use or not use absolute values on the differences being summed." pauldelbrot
DLD {
; Based on https://arxiv.org/pdf/2001.08937.pdf
; ucl file for UltraFractal by pauldelbrot
init:
float sum = 0.0
float lastx = 0.0
float lasty = 0.0
float lastz = 0.0
int i = 0
loop:
float d = |#z|
float dd = 1/(d + 1)
float xx = 2*real(#z)*dd
float yy = 2*imag(#z)*dd
float zz = (d - 1)*dd ; Riemann sphere coordinates
IF (isInf(d) || isNaN(d))
; Infinity, or thereabouts
xx = 0
yy = 0
zz = 1
ENDIF
IF (i > 0)
IF(@qabs)
sum = sum + abs(xx - lastx)^@power + abs(yy - lasty)^@power + abs(zz - lastz)^@power
ELSE
sum = sum + (xx - lastx)^@power + (yy - lasty)^@power + (zz - lastz)^@power
ENDIF
ENDIF
i = i + 1
lastx = xx
lasty = yy
lastz = zz
final:
IF(@qsum)
#index = sum
ELSE
#index = sum/(i - 1)
ENDIF
default:
title = "Discrete Langrangian Descriptors"
param power
caption = "Power"
default = 0.25
hint = "Affects the steepness of the gradient near singularities (fractal features like a Julia set)"
min = 0.0
endparam
param qsum
caption = "Sum"
default = false
hint = "Averages if false, sums if true."
endparam
param qabs
caption = "Abs differences"
default = false
endparam
}
Fragmentarium
[edit | edit source]Code based on the UF code, modified and optimized for GLSL by 3Dickulus[10]
#include "Complex.frag"
#include "MathUtils.frag"
#include "Progressive2D.frag"
#info Unveiling Fractal Structure with Lagrangian Descriptors
#info https://fractalforums.org/fractal-mathematics-and-new-theories/28/unveiling-the-fractal-structure-of-julia-sets-with-lagrangian-descriptors/3376/msg20446#msg20446
#group Lagrangian
// Number of iterations
uniform int Iterations; slider[1,200,1000]
uniform vec3 RGB; slider[(0,0,0),(0.0,0.4,0.7),(1,1,1)]
uniform bool Julia; checkbox[false]
uniform vec2 JuliaXY; slider[(-2,-2),(-0.6,1.3),(2,2)]
uniform float p; slider[0,.6,1]
/* partial pnorm
input: z, c, p
output ppn
*/
float ppnorm( vec2 z, vec2 c, float p){
vec3 s0,s1; // for 2 points on the Riemann sphere
float d; // denominator
float ds;
// map from complex plane to riemann sphere
// z
d = z.x*z.x + z.y*z.y + 1.0;
s0 = vec3(2.0*z,(d-2.0))/d;
// zn
d = c.x*c.x + c.y*c.y + 1.0;
s1 = vec3(2.0*c,(d-2.0))/d;
// sum
vec3 ss = pow(abs(s1 - s0),vec3(p));
ds = ss.x+ss.y+ss.z;
return ds;
}
// DLD = Discret Lagrangian Descriptior
float lagrangian( vec2 z, vec2 c, float p ){
int i; // number of iteration
float d = 0.0; // DLD = sum
for (i=0; i<Iterations; ++i){
d += ppnorm(z, c, p); // sum z
z = cMul(z,z) +c; // complex iteration
if (cAbs(z) > 1e19 ) break; // exterior : upper limit of float type
}
d /= float(i); // averaging not summation
return d;
}
vec3 color(vec2 c) {
vec2 z = Julia ? c : vec2(0.,0.);
if(Julia) c = JuliaXY;
float co = lagrangian( z, c, p );
return .5+.5*cos(6.2831*co+RGB);
}
#preset Default
Center = -0.724636541,0.025224931
Zoom = 0.64613535
EnableTransform = false
RotateAngle = 0
StretchAngle = 0
StretchAmount = 0
Gamma = 2.2
ToneMapping = 1
Exposure = 1
Brightness = 1
Contrast = 1
Saturation = 1
AARange = 2
AAExp = 1
GaussianAA = true
Iterations = 20
RGB = 0,0.4,0.7
p = 0.1444322
Julia = false
JuliaXY = -1.05204872,0
Bailout = 1000
#endpreset
#preset Basilica
Center = -0.025346913,-0.013859176
Zoom = 0.561856826
EnableTransform = false
RotateAngle = 0
StretchAngle = 0
StretchAmount = 0
Gamma = 2.2
ToneMapping = 1
Exposure = 1
Brightness = 1
Contrast = 1
Saturation = 1
AARange = 2
AAExp = 1
GaussianAA = true
Iterations = 20
RGB = 0,0.4,0.7
p = 0.1444322
Julia = true
JuliaXY = -1.05204872,0
Bailout = 1000
#endpreset
c
[edit | edit source]/* partial pnorm
input: z , zn = f(z), p
output ppn
*/
double ppnorm( complex double z, complex double zn, double p){
double s[2][3]; // array for 2 points on the Riemann sphere
int j;
double d; // denominator
double x;
double y;
double ds;
double ppn = 0.0;
// map from complex plane to riemann sphere
// z
x = creal(z);
y = cimag(z);
d = x*x + y*y + 1.0;
s[0][0] = (2.0*x)/d;
s[0][1] = (2.0*y)/d;
s[0][2] = (d-2.0)/d; // (x^2 + y^2 - 1)/d
// zn
x = creal(zn);
y = cimag(zn);
d = x*x + y*y + 1.0;
s[1][0] = (2.0*x)/d;
s[1][1] = (2.0*y)/d;
s[1][2] = (d-2.0)/d; // (x^2 + y^2 - 1)/d
// sum
for (j=0; j <3; ++j){
ds = fabs(s[1][j] - s[0][j]);
ppn += pow(ds,p); // |ds|^p
}
return ppn;
}
// DLD = Discret Lagrangian Descriptior
double lagrangian( complex double z0, complex double c, int iMax, double p ){
int i; // number of iteration
double d = 0.0; // DLD = sum
double ppn; // partial pnorm
complex double z = z0;
complex double zn; // next z
if (cabs(z) < AR || cabs(z +1)< AR) return 5.0; // for z= 0.0 d = inf
for (i=0; i<iMax; ++i){
zn = z*z +c; // complex iteration
ppn = ppnorm(z, zn, p);
d += ppn; // sum
//
z = zn;
if (cabs(z) > ER ) break; // exterior : big values produces NAN error in ppnorm computing
if (cabs(z) < AR || cabs(z +1)< AR)
{ // interior
d = -d;
break;
}
}
d = d/((double)i); // averaging not summation
if (d<0.0) {// interior
d = 2.5 - d;
}
return d;
}
unsigned char ComputeColorOfDLD(complex double z){
int iColor;
double d;
d = lagrangian(z,c, N,p);
iColor = (int)(d*255) % 255; // color is proportional to d
return (unsigned char) iColor;
}
Papers
[edit | edit source]- Unveiling the Fractal Structure of Julia Sets with Lagrangian Descriptors by Víctor J. García-Garrido
- in Communications in Nonlinear Science and Numerical Simulation, Volume 91, December 2020, 105417, a single anonymized review but paywalled
- through arxiv.org, free but not peer-reviewed preprint
www
[edit | edit source]references
[edit | edit source]- ↑ C. Mendoza, A. M. Mancho. The hidden geometry of ocean flows. Physical Review Letters 105 (2010), 3, 038501-1-038501-4.
- ↑ A. M. Mancho, S. Wiggins, J. Curbelo, C. Mendoza. Lagrangian Descriptors: A Method for Revealing Phase Space Structures of General Time Dependent Dynamical Systems. Communications in Nonlinear Science and Numerical Simulation. 18 (2013) 3530-3557
- ↑ C. Lopesino, F. Balibrea-Iniesta, V. J. García-Garrido, S. Wiggins, A. M. Mancho. A theoretical framework for Lagrangian descriptors. International Journal of Bifurcation and Chaos 27, 1730001 (2017).
- ↑ Lagrangian description of the flow field in wikipedia
- ↑ C. Lopesino, F. Balibrea, S. Wiggins, A.M. Mancho. Lagrangian Descriptors for Two Dimensional, Area Preserving Autonomous and Nonautonomous Maps. Communications in Nonlinear Science and Numerical Simulation 27 (1-3) (2015) 40-51.
- ↑ V. J . Garcia Garrido. Unveiling the Fractal Structure of Julia Sets with Lagrangian Descriptors. https://arxiv.org/abs/2001.08937
- ↑ V. J. García-Garrido, F. Balibrea-Iniesta, S. Wiggins, A. M. Mancho, C. Lopesino. Detection of Phase Space Structures of the Cat Map with Lagrangian Descriptors. Regular and Chaotic Dynamics 23, (6) 751-766 (2018).
- ↑ G. G. Carlo and F. Borondo. Lagrangian descriptors for open maps Phys. Rev. E 101, 022208 (2020)
- ↑ Lp space when 0<p <1 in wikipedia
- ↑ fractalforums.org: lagrangian-descriptors-fragment-code
V. J. García-Garrido. Unveiling the fractal structure of Julia sets with Lagrangian descriptors. Communications in Nonlinear Science and Numerical Simulation 91 (2020) 105417.



















![{\displaystyle p\in (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc11ca62a414431ebe4c2411bc5931fa9dfbf66e)


