Fractals/Computer graphic techniques/2D/plane inversion
In Mathematics and logic inversion may refer to ( Disambiguation )
- Involution, a function that is its own inverse (when applied twice, the starting value is obtained)
- Inversion in discrete mathematics, any item that is out of order in a sequence
- Inverse element
- Inversive geometry , like circle inversion, a transformation of the Euclidean plane that maps generalized circles to generalized circles
- Inversion in a point, or point reflection, a kind of isometric (distance-preserving) transformation in a Euclidean space
- Inversion transformation, a conformal transformation (one which preserves angles of intersection)
- Method of inversion, the image of a harmonic function in a sphere (or plane); see [ethod of image charges
- Multiplicative inverse] the reciprocal of a number (or any other type of element for which a multiplication function is defined)
- Matrix inversion, an operation on a matrix that results in its multiplicative inverse
- Model inversion
- Set inversion
inversion of curves and surfaces
[edit | edit source]In inversive geometry ibversion is a transformation of the Euclidean plane, like:
- circle inversion
- Parabola inversion
-
Inversion of a parabola = cardioid
-
Stereographic projection as an inversion of a sphere
plane inversion
[edit | edit source]Plane inversion is an example of plane transformation. Inversion transformation, is a conformal transformation (one which preserves angles of intersection).[1] Inversion can be composite with another transformation, like translation.
parameter plane (with Mandelbrot set) inversion
[edit | edit source]Inversions by plane types
- inversion of standard Mandelbrot set ( c-plane )
- inversion of lambda mandelbrot set ( lambda plane)
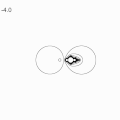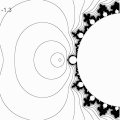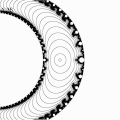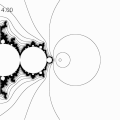
c-plane
[edit | edit source]Description by Nikola Ubavić: Žulijev i Mandelbrotov skup ( in serbian)
- composition of the inversion with respect to the unit circle centered at zero, and the conjugation (axial symmetry with respect to the real line). The cardioid from the boundary of the Mandelbrot set in the "standard" parameterization corresponds to the tear-shaped curve in the 1/c parameterization.
- Inverted c-plane : "Geometrically, the ... relationship between the parameters represents the composition of the inversion with respect to the unit circle centered at zero, and the conjugation (axial symmetry with respect to the real line). Due to this connection, the cardioid from the boundary of the Mandelbrot set in the "standard" parameterization corresponds to the tear-shaped curve in the alpha parameterization."[2]
- "if translation is performed for before the inversion 1/4, then the cardioid is imaged in a parabola"
Description by David E. Joyce: Julia and Mandelbrot Sets. Alternate Parameter Planes
- The inverse of the cardioid is the exterior of a teardrop shape. The circles on the outside of the cardioid are inverted to circles on the inside of the teardrop. The cusp of the cardioid becomes the cusp of the teardrop.
-
c-plane
-
inverted c plane = 1/c plane
-
Inversion of lambda Mandelbrot set with different translations
-
inversion of c family without translation
Continous inversion methods by Arneauxtje
[edit | edit source]Description by Arneauxtje: the transformation from the cardioid of the body of the set to a circle. This is done in c-space (a+ib) as follows:
rho=sqrt(a*a+b*b)-1/4 phi=arctan(b/a) a-new=rho*(2*cos(phi)-cos(2*phi))/3 b-new=rho*(2*sin(phi)-sin(2*phi))/3
Then, there's the 4 different ways on how to get from c to 1/c, that group in 3 families:
- addition: c -> c-c*t+t/c and t=0..1
- multiplication: c -> c/(t*(c*c-1)+1) and t=0..1
- exponentiation: c -> c^t and t=1..-1
The first 2 are pretty elementary to work out. The 3rd makes use of the fact that:
- c = a+ib = r*exp(i*phi) where r=sqrt(a*a+b*b) and phi=arctan(b/a)
- then c^t = r^t*exp(t*i*phi) = r^t*[cos(t*phi)+i*sin(t*phi)]
lambda plane
[edit | edit source]lambda mandelbrot set :
Description by Nikola Ubavić: Žulijev i Mandelbrotov skup ( in serbian)
- "By inverting a complex plane around a unit circle with center at zero, one of these circles remains invariant, while the other image is inside it."
- "If ... translation is performed before the inversion1, then the two circles are mapped into two parallel lines. In this way the second of the next two figures was obtained."
-
lambda plane
-
1/lambda plane
Videos
Dynamic plane ( with Julia set) inversion
[edit | edit source]- f(z) = z^2+c convert to f(z) = z^2 + 1/c
- inverting the polynomial formula Ax(1-x) in the circle of radius 1, resulting in the formula f(x)= x^2/A(1-x).[3]
- Imploded cauliflower
-
z plane with BD
-
w = 1/z plane with BD
basilica
[edit | edit source]- normal basilica f(z) = z^2 - 1
- inverted basilica
- rational with degree = 2 : reversed basilica[4] : f(z) = z^2/(z^2 -1)
-
Basilica
-
reversed basilica
-
Inverted basilica as a boundary of region containing critical point and it's preimages
Videos