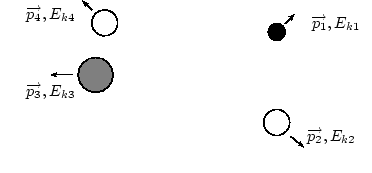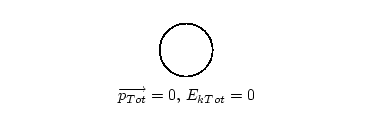When an object explodes, it breaks up into more than one piece and it therefore changes its shape. Explosions occur when energy is transformed from one kind e.g. chemical potential energy to another e.g. heat energy or kinetic energy extremely quickly.
So, like in inelastic collisions, total kinetic energy is not conserved in explosions. But total momentum is always conserved. Thus if the momenta of some of the parts of the exploding object are measured, we can use momentum conservation to solve the problem!

|
The Tunguska event was an aerial explosion that occurred near the Podkamennaya (Stony) Tunguska River in what is now Evenkia, Siberia, at 7:17 AM on June 30, 1908. The size of the blast was
later estimated to be equivalent to between 10 and 15 million tons of regular explosive. It felled an estimated 60 million trees over 2,150 square kilometers.
At around 7:15 AM, Tungus natives and Russian settlers in the hills northwest of Lake Baikal observed a huge fireball moving across the sky, nearly as bright as the Sun. A few minutes later, there was a flash that lit up half of the sky, followed by a shock wave that knocked people off their feet and broke windows up to 650 km away (the same as the distance from Bloemfontein to Durban!). The explosion registered on seismic stations across Europe and Asia, and produced fluctuations in atmospheric pressure strong enough to be detected in Britain. Over the next few weeks, night skies over Europe and western Russia glowed brightly enough for people to read
by.
Had the object responsible for the explosion hit the Earth a few hours later, it would have exploded over Europe instead of the sparsely-populated Tunguska region, producing massive loss of human
life.
|
In the following picture, a closed can of baked beans is put on a
stove or fire:

Before the can heats up and explodes, the total momentum
of the system is:

and the total kinetic energy of the system is:

since the can isn't moving. Once the mixture of beans, juice and air inside the can reach a certain temperature, the pressure inside the can becomes so great that the can explodes! Beans and sharp pieces of metal can fly out in all directions. Energy in the system has been transformed from heat energy into kinetic energy.
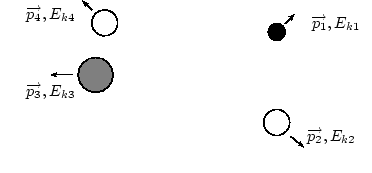
After the explosion, the can is completely destroyed. But momentum is always conserved, so:

However, the kinetic energy of the system is not conserved. The can's shape was changed in the explosion. Before the explosion the can was not moving, but after the explosion, the pieces
of metal and baked beans were moving when they were flying out in all directions! So:

| Safety tip: Never heat a closed can on a stove or fire!
|
| Always open the can or make a hole in the lid to allow the pressure inside and outside
|
| the can to remain equal. This will prevent the can from exploding!
|
Question: An object with mass mTot = 10 kg is sitting at rest. Suddenly it explodes into two pieces. One piece has a mass of m1 = 5 kg and moves off in the
negative x-direction at  . What is the velocity of the other piece?
. What is the velocity of the other piece?
Answer:
Step 1 :
Draw the picture. Before the explosion, the object is at rest:
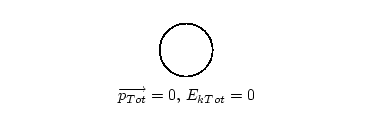
After the explosion, the two pieces move off:
Riaan Note: second image on page 154 is missing
File:Fhsst expl16.png
Step 2 :
Now we know that in an explosion, total kinetic energy is not conserved. There is a definite change in shape of the exploding object! But we can always use momentum conservation to solve the problem.
So:

But the object was initially at rest so:

Step 3 :
Now we know that m1= 5 kg but we do not know what the mass of m2 is. However, we do know that:

Step 4 :
Now we can substitute all the values we know into equation (A) and solve for  . Let's choose the positive x-direction to have a positive sign and the negative x-direction to have a negative sign:
. Let's choose the positive x-direction to have a positive sign and the negative x-direction to have a negative sign:

Therefore,

Question: An object with mass mTot =15 kg is sitting at rest. Suddenly it explodes into two pieces. One piece has a mass of m1 = 5000 g and moves off in the
positive x-direction at  . What is the final velocity of the other piece?
. What is the final velocity of the other piece?
Answer:
Step 1 :
Draw the picture. Before the collision:

After the collision:
Riaan Note: image on page 156 is missing
File:Fhsst expl18.png
Step 2 :
Convert all units into S.I. units:

Step 3 :
Now we know that in an explosion, total kinetic energy is not conserved. There is a definite change in shape of the exploding object! But we can always use momentum conservation to solve the problem. So:

But the object was initially at rest so:

Step 4 :
Now we know that m1= 5 kg but we do not know what the mass of m2 is. However, we do know that:

Step 5 :
Now we can substitute all the values we know into equation (A) and solve for  . Let's choose the positive x-direction to have a postive sign and the negative x-direction to have a negative sign:
. Let's choose the positive x-direction to have a postive sign and the negative x-direction to have a negative sign:

Therefore,