Consciousness Studies/The Neuroscience Of Consciousness
"All parts of the brain may well be involved in normal conscious processes but the indispensable substratum of consciousness lies outside the cerebral cortex, probably in the diencephalon" Penfield 1937.
"The brain stem-thalamocortical axis supports the state, but not the detailed contents of consciousness, which are produced by cortex" Baars et al 1998.
Introduction
[edit | edit source]It is recommended that readers review The Philosophical Problem before reading the sections on the neuroscience of consciousness.
One of the most exciting discoveries of neuroscience is that nearly all of the brain performs functions that are not part of conscious experience. In everyday life we are usually unaware of breathing or heartbeats yet there are parts of the brain dedicated to these functions. When we pick up a pencil we have no experience of the fine control of individual muscles yet large areas of cortex and cerebellum implement this. Things do not appear as greyscale and then have the colour poured into them although this strange colour addition is done in the visual cortex. Most of the brain is non-conscious but how is the "ghost in the machine", the mind, created by and linked into the mostly non-conscious brain?
Although most of the processes in the brain are non-conscious there can be little doubt that the output of sensory processes contribute to experience. For example, although we do not experience the process of adding colour to visual data in cortical area V4 we do experience coloured forms and although we have little inkling of the hugely complex creation of words in the temporal/frontal lobes we do experience verbal thoughts. Our experience is an integrated output of most of the brain processes that deal with sensation as well as dreams, thoughts and emotions. But how and where does this experience occur?
The signals that compose phenomenal consciousness have not been elucidated. Perhaps the least likely signals for this role are electrical impulses in nerve fibres because they are distributed unevenly in time and space and can even be absent for relatively long periods. Furthermore, electrical impulses across the membranes of neurons have an all or nothing character; they cannot be easily superimposed on one another. There are many other possibilities however, such as: the electrical fields on the dendrites of neurons, the fields of chemicals spreading out from synapses, the radio-frequency emissions of action potentials, events in the microtubules in cells, the depolarisations of glia, the varying fields measured by EEG devices, the quantum superposition of brain states etc...
Phenomenal consciousness could exist in the dendritic field of ten neurons receiving 100,000 synapses or as an oscillation of fields over the whole brain. The substrate of phenomenal consciousness could be staring us in the face as a state of the whole brain or be like a needle in a haystack, lurking in a tiny region of brain, unsuspected and undiscovered.
Given that there is no widely accepted theory of phenomenal consciousness Crick (1994) and Crick and Koch (1998) approached the problem of the location of the substrate of consciousness by proposing that scientists search for the Neural Correlates of Consciousness. These neural correlates consist of events in the brain that accompany events in conscious experience.
References:
Crick, F. (1994). The Astonishing Hypothesis. New York: Scribners.
Crick, F. & Koch, C. (1998).Consciousness and Neuroscience. Cerebral Cortex, 8:97-107, 1998 http://www.klab.caltech.edu/~koch/crick-koch-cc-97.html
Neuroanatomy
[edit | edit source]General layout of the CNS
[edit | edit source]The Central Nervous System (CNS) consists of the spinal cord, the brain and the retina.
The CNS consists of two major groups of active cells, the neurons and the glia. The neurons conduct short impulses of electricity along their membranes called 'action potentials and encode data as frequency modulated signals (i.e.: different intensities of stimulation are converted into different rates of firing). The glia modify the connections between neurons and can respond to neuron activity by a change of voltage across their membranes. Glia also have many other roles such as sustaining neurons and providing electrical insulation.
Neurons have three principal parts: the cell body, the dendrites and the axon. Impulses flow from the cell body to the axon. The axon can be over a metre long and bundles of axons form nerve fibres. Where an axon makes contact with the dendrites or cell body of another neuron there is a special sort of junction called a synapse. Transmission of data across synapses is usually mediated by chemical signals.
Areas of the brain where there are many cell bodies have a beige/grey tinge and are called grey matter. Areas that contain mainly nerve fibres are called white matter. Masses of grey matter outside of the surface of the cerebral cortex or the cerebellum are called nuclei.
The brain is of central interest in consciousness studies because consciousness persists even when the spinal cord is sectioned at the neck.
The brain can be divided into five distinct divisions or vesicles on the basis of embryological development. These are the myelencephalon, metencephalon, mesencephalon, diencephalon and telencephalon (See the illustration below).
- Myelencephalon: Medulla oblongata.
- Metencephalon: pons and cerebellum.
- Mesencephalon: midbrain (tectum containing the superior colliculus and inferior colliculus, red nucleus, substantia nigra, cerebellar peduncles.
- Diencephalon: thalamus, epithalamus, hypothalamus, subthalamus.
- Telencephalon: corpus striatum, cerebral hemispheres.
These divisions tend to obscure the physical anatomy of the brain which looks like a rod of spinal cord with a swelling at the top due to the thalamus and corpus striatum. Around the top of the rod is a globe of deeply indented cerebral cortex and at the back there is the puckered mass of cerebellum. The physical anatomy is shown in greater detail in the illustration below where the thalamus and corpus striatum have been splayed out to show more detail.
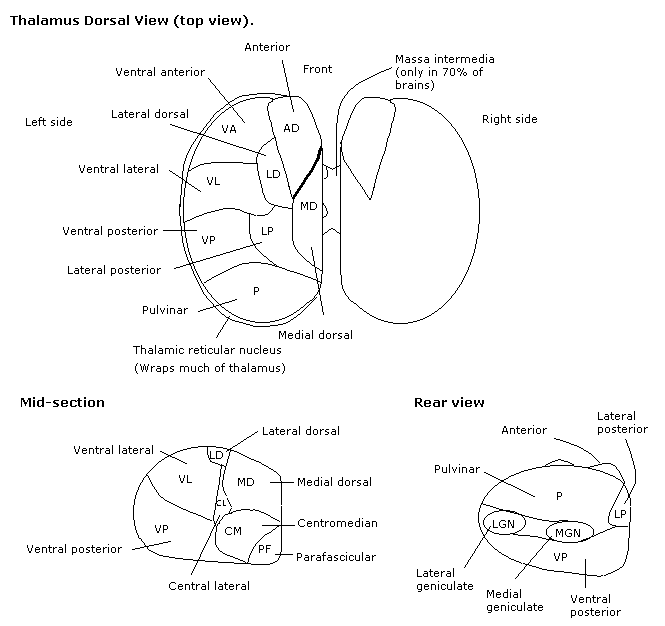
The thalamus is a complex organ with numerous nuclei. These are listed below:
| Type of Nucleus | Name | Abbrev | Function |
|---|---|---|---|
| Reticular | Reticular | R | Arousal |
| Intralaminar | Centromedian | CM | Arousal, attention, motivation, pain |
| Parafascicular | Pf | ||
| Central lateral | CL | ||
| Paracentral | Pcn | ||
| Intralaminar Midline | Reunions | Re | |
| Paraventricular | Pv | ||
| Rhomboid | |||
| Nonspecific | Pulvinar | P | Association |
| Lateral dorsal | LD | ||
| Anterior | AD | ||
| Anteromedial | AM | ||
| Anteroventral | AV | ||
| Lateral posterior | LP | ||
| Medial Dorsal | MD | ||
| Specific Thalamic Nuclei | Lateral geniculate | LGN | Vision |
| (Sensory Relays) | Medial geniculate | MGN | Auditory |
| Ventral posterior | VP | General sensation | |
| Specific Thalamic Nuclei | Ventral anterior | VA | Motor |
| (motor) | Ventral lateral | VL | Motor |
The location of these nuclei is shown in the illustration below:
The cerebral hemispheres consist of a thin layer of nerve cell bodies on the surface (the cerebral cortex) with a mass of white, interconnecting fibres below (the cerebral medulla). Each hemisphere is divided into four principle lobes as shown in the illustration below:
The cortex is a set of interconnected processors. The general layout of the cortex with the location of the processors is shown in the illustration below:
The pathways in the brain tend to preserve the topography of the sense organs so that particular groups of cells on the retina, cochlear or body have corresponding groups of cells in the thalamus or cortex. The retina is said to have a topological mapping onto the thalamus so that the projection of the optic nerve is said to be retinotopic.
Nerve fibres that go to a part of the brain are called afferents and fibres that come from a part of the brain are called efferents.
The cortex and thalamus/striatum are intimately linked by millions of connecting fibres and there is also a direct connection from the motor cortex to the spinal cord.
Sensory pathways
[edit | edit source]Information from the sense organs travels along the appropriate sensory nerve (optic, auditory, spinal etc.) and once in the brain is divided into three principal paths that connect either with the thalamus, the cerebellum or the reticular formation.
There are thalamic nuclei for each broad type of sensation and these have reciprocal connections with specific areas of cortex that deal with the appropriate mode of sensation. The large mass of nerve fibres that mediate the connection between the thalamus and cortex are known as the thalamo-cortical and cortico-thalamic tracts. There tend to be more sensory nerve fibres returning from the cortex to the thalamus than connect from the thalamus to the cortex so it is difficult to determine whether the cortex is the destination of sensory data or a region that supplies extra processing power to thalamic nuclei.
The cerebellum mediates reflex control of complex movements and receives input from most of the sense organs.
The reticular formation is a group of loosely distributed neurons in the medulla, pons and mesencephalon. It receives a large amount of autonomic input and also input from all the sense organs. The intralaminar nuclei of the thalamus are the principal destination of reticular output to higher centres. In the most primitive vertebrates the reticular formation performs most of the higher control functions of the animal. The reticular formation is implicated in the maintenance of sleep-wake cycles and activates the higher centres. This activity has attracted the label ascending reticular activating system (ARAS) to describe how the activity of higher centres is controlled by reticular input. This title is unfortunate from the point of view of consciousness studies because it implies that conscious experience is a result of activating the cortex when it could be due to turning on or off particular systems all the way from the reticular formation to the cortex. Destruction of the reticular formation leads to coma.
Motor and output pathways
[edit | edit source]Motor control of the body below the skull is accomplished by three principle routes.
The motor cortex of the frontal lobes and related cortex in the parietal lobes can control movement directly via nerves known as the cortico-spinal tract (also called the pyramidal tract). The activity of the motor cortex is modified and controlled by a loop that passes through the corpus striatum, the substantia nigra and the subthalamic nucleus and returns to the cortex. These controlling nuclei are, along with the amygdala, known as the basal ganglia.
The cerebellum and the corpus striatum provide complex reflex control of the body through nerves that travel through the red nucleus and form the rubro-spinal tract.
The vestibular nucleus, which processes signals related to balance and posture, has direct connections with the periphery via the vestibulo-spinal tract.
Apart from the routes for controlling motor activity there are also other outputs from the brain, for instance the autonomic nervous system is intimately linked with the reticular formation which has areas that control blood pressure, respiratory rhythm etc.
Topological mapping and cortical columns
[edit | edit source]
The cerebral cortex has a highly convoluted surface that provides a large area of tissue. The parts of the cortex that are used for motor and sensory functions are organised so that different areas correspond to different zones of the body. This topological organisation is shown classically by a drawing of the sensorimotor homunculus such as that shown on the right.
Within a given area of the cortex there are further subdivisions. For example, the occipital cortex corresponds to the eyes of the sensorimotor homunculus and it is further organised so that areas of the retina have corresponding areas on the cortex. This mapping of the layout of the retina onto the cortex is known as topological mapping. It results in a corresponding mapping of the receptive field of the eye onto the cortex. The mapping is like an image on the surface of the brain tissue and the visual scene that is presented to a subject can be recovered by using fMRI along with computer analysis (Miyawaki et al. 2008).
The human cortex is fairly deep, containing 100-200 neurons from the surface to the white matter. It is divided into six histological and functional layers. These layers can be further subdivided. In 1957 Mountcastle used microelectrode measurements to show that activity of small zones of cortex about 0.1 to 1 mm in diameter corresponded to particular points in the receptive field. These functional columns of cortical tissue are called cortical columns.
The diagram above shows the organisation of ocular dominance columns. Each column represents a particular part of the receptive field of a single eye. The columns for left and right eyes are linked together in lines. The lines of ocular dominance form a pattern like a fingerprint on the surface of the cortex.
The same part of cortex can have overlapping columns for different functions. For instance there are columns that react to particular orientations of edges at particular places in the visual field. These columns tend to be located together on the cortex forming a pinwheel of columns that cover all orientations at a particular receptive field position.
There are also topologically arranged columns for colour, spatial frequency etc.
Yoichi Miyawaki, Hajime Uchida, Okito Yamashita, Masa-aki Sato, Yusuke Morito, Hiroki C. Tanabe, Norihiro Sadato and Yukiyasu Kamitani. (2008). Visual Image Reconstruction from Human Brain Activity using a Combination of Multiscale Local Image Decoders. Neuron, Volume 60, Issue 5, 10 December 2008, Pages 915-929
Modules