Circuit Theory/Y Δ
Jump to navigation
Jump to search

Circuit after Δ Y transformation of top bridge .. can now use parallel/serial combinations rather than source injection to find Thevenin's resistance 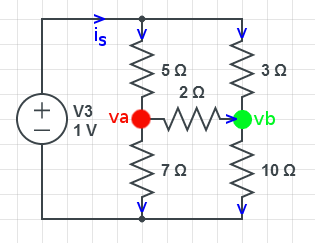
Example23g.png 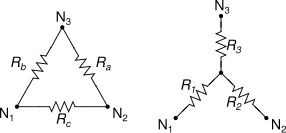

The bridge circuit example was solved with source injection, but could have been solved with a Y Δ transformation.

The 5,2 and 3 ohm resistors form a Δ that could be transformed into a Y.

The equations are:
Now Thevenin's resistance can be solved by parallel and serial combinations:
Which is the same value found through source injection.


