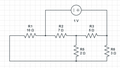
Circuit Theory/Thevenin-Norton

Vth using Node

opening load, finding V_th using Node .. code

$V_{th} = 6.4516$

In using Node

shorting load, finding I_n using Node .. code

$I_N = 1.064773736$

Rth or Rn

$V_{th}/I_N= \frac{6.4516}{1.064773736} = 6.0591 ohms$

Finding Rth using source injection and node

• 

  zero sources to find Rth

• 

  add source injection since parallel/series combinations do not exist

• 

  redraw up and down before solving

Here is the mupad/matlab code that generates the answer R_th = 6.0591 ohms.

Comparing Node with Thevenin Equivalent

solving using Node .. code

solving using Thevenin equivalent

Solving the node equations yields:

$V_a = 5.393$

$V_b = 1.1673$

$V_c = 1.107$

$i_{12} = 0.3571$

$v_{12} = 4.286$

Using the Thevenin equivalent (and voltage divider) to compute voltage across the 12 ohm resistor:

$v_{12} = V_s*\frac{12}{R{total}}$

$v_{12} = 6.4516*\frac{12}{6.0591+12} = 4.287$

So they match ...

Thevenin voltage and resistance can not be computed from a node analysis of the entire circuit, but the node analysis of the entire circuit can be used to check if the thevenin equivalent produces the same numbers.