Circuit Theory/Simultaneous Equations/Example 5

example 5 circuit

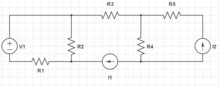
Find currents and voltages. Assume the sources and resistance values are knows. Solve symbolically.

From a practical point of view, putting more than one power supply in a circuit is bad practice. Almost everyone tries to design circuits with only one power supply.

From a modeling point of view, transistors at the first level of approximation are a type of power supply. So putting multiple power supplies in a circuit is practice or preparation for more complicated circuits.

Label

symbols have been added

There is one voltage source, in series with a resistor to get its current from: $i_{R1}$. The two current sources had no clear resistor in parallel with them from which to get their voltage, so voltages for each had to be labeled: $i_{I1}$ and $i_{I2}$.

Loops

loops and the + - added

There are three loops. Remember that the + and - right now are not guessing the polarity of the answer, but are capturing the layout of the circuit.

There are no trivial loops (components in parallel).

Junctions

constant EMF sections highlighted

Junctions chosen and current directions put on drawing

There are two trivial junctions where series components share the same current. One is between the voltage source and $R_{1}$. The other is between current source $I_{2}$ and $R_{5}$.

There are four non-trivial junctions, see the areas constant EMF that are shaded in different colors.

This means that three junctions that can be used. It doesn't matter which three were chosen. But three have to be chosen and then currents placed relative to the voltage polarity on the resistors. The two branches where there are current sources don't need additional current symbols made up for them, just like the voltage source does need a voltage symbol made up for it.

Count Eq

We are being told that the resistors and voltage sources have values, and are thus to be treated as knowns. We just don't know what the specific values are so we have to work symbolically.

$R_{1}=\surd$
$R_{2}=\surd$
$R_{3}=\surd$
$R_{4}=\surd$
$R_{5}=\surd$
$I_{1}=\surd$
$I_{2}=\surd$
$V_{1}=\surd$
$i_{R1}=?$
$i_{R2}=?$
$i_{R3}=?$
$i_{R4}=?$
$v_{R1}=?$
$v_{R2}=?$
$v_{R3}=?$
$v_{R4}=?$
$v_{R5}=?$
$v_{I1}=?$
$v_{I2}=?$

There are 11 unknowns. There are 5 equations from the resistors, 3 from the loops and 3 from the junctions. So the problem can be solved explicitly.

Terminal Eq

$v_{R1}=i_{R1}*R_{1}$
$v_{R2}=i_{R2}*R_{2}$
$v_{R3}=i_{R3}*R_{3}$
$v_{R4}=i_{R4}*R_{4}$
$v_{R5}=-I_{2}*R_{5}$
The current $I_{2}$ is negative, because it is going into the negative terminal of $R_{5}$.

When there are lots of power sources, the direction of their currents or the polarity of the sources has to be captured by the equations.

If this direction is mistaken, often the answer magnitudes turn out correct but the sign is wrong. The point is that the answers are very similar. The problem is usually that the sign convention is messed up some how.

Loop Eq

$L_{1}:v_{R2}+v_{R1}-V_{1}=0$
$L_{2}:v_{R3}+v_{R4}+v_{I1}-v_{R2}=0$
$L_{3}:v_{R5}+v_{I2}-V_{R4}=0$

The voltage polarities of the current sources were chosen arbitrarily, but a choice has to be made. The choice has to be documented on the drawing, and then reflected in the equations. Otherwise the equations can not be checked.

Junction Eq

$J_{1}:i_{R1}-i_{R2}-i_{R3}=0$
$J_{2}:i_{R3}+I_{2}-i_{R4}=0$
$J_{3}:i_{R4}-I_{2}-I_{1}=0$

Solve the Equations

Algebra

The algebra solution is massive, messy, hard to check and doesn't inspire anyone. Not going to attempt it.

Differential Equations

There are none in this problem, but three quarters of this course is going over circuits this complex with capacitors and inductors instead of resistors and looking at the differential equations.

Symbolic Computations

Mathematica

File:Ex5-6.png

Mathematica solution. Click here for text to enter into Mathematica.

Wolfram Alpha doesn't work with more than 6 or 7 equations no matter what their form. Going to do in Mathematica. Then do in MuPAD. Then compare the answers.

MuPad

File:Ex5-7.png

MathWorks MuPAD solution .. click here for the text to cut and paste .. MuPad Solution contains variable solution

MuPAD's answers match with Mathematica, but the format of the more complicated answers is very different. The goal would then be to use some kind of simplify command, but alternative symbols can be used to express the same answer. Look at $V_{I2}$ answers. They are the same, but they use different symbols.

In fact, here is another answer:

$V_{I1}={\frac {(R_{1}+R_{2})}{R_{1}*R_{2}}}*({\frac {V_{1}}{R_{1}}}-I_{1})-R_{3}*I_{1}-R_{4}*(I_{1}+I_{2})$

File:Ex5-7r.png

Mathematica solution simplied with the simplify command .. looks closer to MuPAD solution

Playing around with simplify and expand commands helps a little. There are all sorts of options associated with the simplify command that lead into a domain of symbolic computation that looses focus on this course. There is no immediate agreement among the packages to the solution of complicated expressions. A visual check of everything but $V_{I1}$ is a match.

The only other quick way to check is to plug in a random set of numbers and see if the two solutions come up with the same numeric solution. But enough time has been spent on this.

Numeric Solution

There is no numeric solution because no numbers were given.

Simulate

Simulation is impossible with out numbers.

Build Intuition

• Complicated expressions have no universal form that symbolic computation agrees upon. So checking them is an algebraic process, or can trust that inserting numbers and showing they match means the symbolic expressions are the same.
• The direction choices when the variables were defined implied that the $V_{1}$ was dumping energy into the circuit. Looking at the solution, it appears that $I_{R1}$, the current through $V_{1}$ is positive. Thus it remains that $V_{1}$ is pumping energy into the circuit.
• The direction choices when the variables were defined implied that the $I_{2}$ was dumping energy into the circuit. Looking at the solution, it appears that $V_{I2}$, the voltage across $I_{2}$ is positive. Thus it remains that $I_{2}$ is pumping energy into the circuit.
• The direction choices when the variables were defined implied that the $I_{1}$ was taking energy out of the circuit and charging its batteries. However, looking at the solution, it appears that $V_{I2}$, the voltage across $I_{1}$ is negative. Thus it seems that in reality $I_{1}$ is also pumping energy into the circuit.