Circuit Idea/Linear Mode of Voltage Inversion NIC
Circuit idea: Making the negative feedback dominate over the positive one.

Introduction
[edit | edit source]What a VNIC operating in linear mode is
[edit | edit source]Negative impedance (resistance) converter with voltage inversion (VNIC) is a true negative resistor having an S-shaped IV curve (Fig. 1a). This composed circuit consists of two components (Fig. 1b): a "positive" resistor R and an amplifier with gain of 2 that amplifies the voltage drop across the resistor. The positive resistor and the amplifier's output are connected in series. The amplifier is implemented by the op-amp OA and the two equal resistors R1 and R2 constituting a voltage divider with ratio 0.5. In this way, the resistor R converts the flowing current into a voltage drop; then, the op-amp amplifies it two times and adds its output voltage in series to the voltage drop. Half the voltage compensates the voltage drop across the resistor R and the rest half remains. Thus the op-amp circuit behaves as a voltage source producing a voltage VOA that is equivalent to the voltage drop across the resistor R (VOA = VR = R.I). The op-amp as though converts the "positive" resistance R into a negative one; that is why, this circuit is named negative impedance converter. As the voltage across the circuit has an opposite polarity to the voltage drop across the initial "positive" resistor R, it is named negative impedance converter with voltage inversion.
How to investigate the linear mode of VNIC
[edit | edit source]VNIC is a two-terminal circuit; so, to give an idea of how it operates, we have to measure its IV curve. For this purpose, we have to pass a varying input current through the circuit and to measure the output voltage between its terminals. There are seven typical for the circuit operation points over the IV curve representing the corresponding six circuit states. For each of them, we may draw the corresponding picture of partial IV curve (from beginning to the current point) and the corresponding circuit diagram representing the current state. Let's label the first sequence of pictures with extension "a" and place them on the left; accordingly, to label the second sequence of pictures with extension "b" and place them on the right.


Investigating the circuit at ideal driving conditions
[edit | edit source]The ideal input source for a VNIC acting in linear mode is the constant current source (CCS). If we begin sinking a current from VNIC (Fig. 2b), it creates a voltage drop VR across the resistor R and the voltage of the inverting input decreases (figuratively speaking, the input current source "pulls down" the bottom end of the resistor R toward the ground). The op-amp increases its output voltage trying to restore the equilibrium (it "pulls up" the top end of the resistor R toward the positive supply rail).
Bottom positive resistance region
[edit | edit source]Negative input current, negative output voltage
[edit | edit source]From the initial point 0 to point 1 (Fig. 2a) we sink a big enough current |IIN| > VSAT+/R from VNIC so that the voltage drop VR (Fig. 2b) is bigger than the positive voltage supply. As a result, the op-amp is in positive saturation but the voltage of the inverting input and the VNIC input voltage (across its two terminals) is negative. The circuit has positive resistance; it behaves as a real voltage source with a constant voltage VSAT+ and an internal resistance R (see the equivalent circuit on the left side of Fig. 2b). It is represented by a linear IV curve on Fig. 2a (the part from point 0 to point 1).


Negative input current, zero output voltage
[edit | edit source]At point 1 (Fig. 3a), we sink a relatively moderate current |IIN| = VSAT+/R from VNIC so that the voltage drop VR is equal to the positive saturation voltage. The op-amp continues staying in positive saturation (Fig. 3b) but the voltage of the inverting input and the VNIC input voltage is zero. The circuit has positive resistance; it continues behaving as a real voltage source.


Negative input current, positive output voltage
[edit | edit source]From point 1 to point 2 (Fig. 4a), we sink a moderate current VSAT+/2R < |IIN| < VSAT+/R from VNIC so that the voltage drop VR is less than the positive saturation voltage (Fig. 4b). But as the voltage of the inverting input is less than the voltage of the non-inverting input, the op-amp continues staying in positive saturation and the voltage of the inverting input (the VNIC input voltage) is positive. The circuit possesses a positive resistance; it continues behaving as a real voltage source.


Middle negative resistance region
[edit | edit source]Negative input current, positive output voltage
[edit | edit source]The “magic” of negative resistance begins at point 2. From point 2 to point 3 (Fig. 5a), we sink a low current |IIN| < VSAT+/2R from VNIC so that the voltage drop VR is less than the half positive saturation voltage (Fig. 5b). The op-amp goes out of saturation and begins operating in active region. The voltage of the inverting input is almost equal to the voltage of the non-inverting input. The input current decreases continuously and the output voltage decreases as well. As a result, the op-amp IV curve moves up and the crossing operating point slides over a new dynamic IV curve representing the negative resistance. Note it is not a real IV curve; it is an artificial, imaginary IV curve having a negative slope and passing through the origin of the coordinate system. The whole circuit behaves as a "helping" dynamic voltage source that is connected in series and in the same direction with the input current source.


Zero input current, zero output voltage
[edit | edit source]At point 3 (Fig. 6a) there is no input current. There is no voltage drop VR across the resistor R (Fig. 6b) and the op-amp produces zero output voltage. A virtual ground appears at the inverting input and the whole circuit behaves as just a resistor R. On the graphical presentation, the op-amp IV curve crosses the origin.


Positive input current, negative output voltage
[edit | edit source]From point 3 to point 4 (Fig. 7a), we begin injecting a low current IIN < |VSAT-|/2R to VNIC so that the voltage drop VR is less than the half negative saturation voltage (Fig. 7b). The op-amp continues operating in active region and the voltage of the inverting input is almost equal to the voltage of the non-inverting input. The input current increases continuously and the output voltage increases as well. The op-amp IV curve continues moving up and the crossing operating point continues sliding over the negative resistance IV curve. The whole circuit continues behaving as a "helping" dynamic voltage source connected in series and in the same direction with the input current source.


Top positive resistance region
[edit | edit source]Positive input current, negative output voltage
[edit | edit source]From point 4 to point 5 (Fig. 8a), we inject a moderate current |VSAT-|/2R < IIN < |VSAT-|/R into VNIC so that the voltage drop VR is less than the negative saturation voltage (Fig. 8b). But as the voltage of the non-inverting input is more negative than the voltage of the inverting input, the op-amp continues staying in negative saturation and the voltage of the inverting input (the VNIC input voltage) is negative. The circuit possesses a positive resistance; it behaves again as a real voltage source with a constant voltage V and an internal resistance R.


Positive input current, zero output voltage
[edit | edit source]At point 5 (Fig. 9a), we inject a relatively moderate current IIN = |VSAT-|/R into VNIC so that the voltage drop VR is equal to the negative saturation voltage. The op-amp continues staying in negative saturation (Fig. 9b) but the voltage of the inverting input and the VNIC input voltage is zero. The circuit has positive resistance; it continues behaving as a real voltage source.

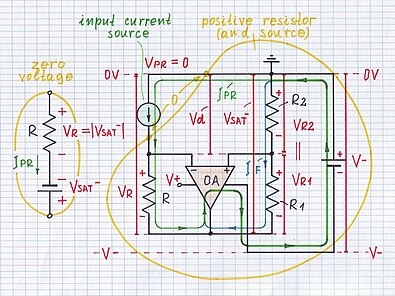
Positive input current, positive output voltage
[edit | edit source]From point 5 to the final point 6 (Fig. 10a) we inject a big current IIN > |VSAT-|/R into VNIC so that the voltage drop VR is bigger than the negative voltage supply (Fig. 10b). As a result, the op-amp continues staying in negative saturation but the voltage of the inverting input and the VNIC input voltage (across its two terminals) is positive. The circuit has positive resistance again; it behaves as a real voltage source (see the equivalent circuit on the left side of Fig. 10b). It is represented by a linear IV curve on Fig. 10a (the part from point 5 to point 6).


Investigating the circuit at real driving conditions
[edit | edit source]In this case, we drive the VNIC by a real voltage source with voltage V and internal resistance Ri.
How to make VNIC operate in linear mode
[edit | edit source]What is the relation between VNIC and inverting amplifier?
[edit | edit source]Conclusions
[edit | edit source]VNIC, like every electronic device, has a finite input range that is limited by the power supply. If the input current does not exceed the maximum magnitude - |IIN| < |VSAT|/2R (from point 2 to point 4), the op-amp is in active region. The whole circuit behaves as a true negative resistor with resistance -R. When the input current exceeds the maximum magnitude - |IIN| > |VSAT-|/2R (from point 0 to point 2) or |IIN| > VSAT+/2R (from point 4 to point 6), the “magic” of negative resistance ceases and the op-amp saturates. In these regions, the whole circuit behaves as a real voltage source with a constant voltage VSAT-/VSAT+ and an internal resistance R.
See also
[edit | edit source]Revealing the mystery of negative impedance
Investigating the linear mode of negative impedance converters with current inversion
Negative impedance converter from Wikipedia considers NIC with current inversion (INIC).
References
[edit | edit source]
External links
[edit | edit source]- Understanding negative impedance converters (VNIC) - reveals in three consecutive steps the basic idea behind VNIC.
- How to compensate resistive losses by series connected negative resistors
- How do we make decreased, zero and negative resistance?
- Nonlinear Circuit Analysis