Calculus/Continuity
Defining Continuity
[edit | edit source]We are now ready to define the concept of a function being continuous. The idea is that we want to say that a function is continuous if you can draw its graph without taking your pencil off the page. But sometimes this will be true for some parts of a graph but not for others. Therefore, we want to start by defining what it means for a function to be continuous at one point. The definition is simple, now that we have the concept of limits:
If is defined on an open interval containing , then is said to be continuous at if and only if .
Note that for to be continuous at , the definition in effect requires three conditions:
- that is defined at , so exists,
- the limit as approaches exists, and
- the limit and are equal.
If any of these do not hold then is not continuous at .
The idea of the definition is that the point of the graph corresponding to will be close to the points of the graph corresponding to nearby -values. Now we can define what it means for a function to be continuous in general, not just at one point.
A function is said to be continuous on if it is continuous at every point of the interval .
We often use the phrase "the function is continuous" to mean that the function is continuous at every real number. This would be the same as saying the function was continuous on , but it is a bit more convenient to simply say "continuous".
Note that, by what we already know, the limit of a rational, exponential, trigonometric or logarithmic function at a point is just its value at that point, so long as it's defined there. So, all such functions are continuous wherever they're defined. (Of course, they can't be continuous where they're not defined!)
Discontinuities
[edit | edit source]A discontinuity is a point where a function is not continuous. There are lots of possible ways this could happen, of course. Here we'll just discuss two simple ways.
Removable discontinuities
[edit | edit source]The function is not continuous at . It is discontinuous at that point because the fraction then becomes , which is undefined. Therefore the function fails the first of our three conditions for continuity at the point 3; 3 is just not in its domain.
However, we say that this discontinuity is removable. This is because, if we modify the function at that point, we can eliminate the discontinuity and make the function continuous. To see how to make the function continuous, we have to simplify , getting . We can define a new function where . Note that the function is not the same as the original function , because is defined at , while is not. Thus, is continuous at , since . However, whenever , ; all we did to to get was to make it defined at .
In fact, this kind of simplification is often possible with a discontinuity in a rational function. We can divide the numerator and the denominator by a common factor (in our example ) to get a function which is the same except where that common factor was 0 (in our example at ). This new function will be identical to the old except for being defined at new points where previously we had division by 0.
However, this is not possible in every case. For example, the function has a common factor of in both the numerator and denominator, but when you simplify you are left with , which is still not defined at . In this case the domain of and are the same, and they are equal everywhere they are defined, so they are in fact the same function. The reason that differed from in the first example was because we could take it to have a larger domain and not simply that the formulas defining and were different.
Jump discontinuities
[edit | edit source]Not all discontinuities can be removed from a function. Consider this function:
Since does not exist, there is no way to redefine at one point so that it will be continuous at 0. These sorts of discontinuities are called nonremovable discontinuities.
Note, however, that both one-sided limits exist; and . The problem is that they are not equal, so the graph "jumps" from one side of 0 to the other. In such a case, we say the function has a jump discontinuity. (Note that a jump discontinuity is a kind of nonremovable discontinuity.)
One-Sided Continuity
[edit | edit source]Just as a function can have a one-sided limit, a function can be continuous from a particular side. For a function to be continuous at a point from a given side, we need the following three conditions:
- the function is defined at the point.
- the function has a limit from that side at that point.
- the one-sided limit equals the value of the function at the point.
A function will be continuous at a point if and only if it is continuous from both sides at that point. Now we can define what it means for a function to be continuous on a closed interval.
A function is said to be continuous on if and only if
- it is continuous on .
- it is continuous from the right at .
- it is continuous from the left at .
Notice that, if a function is continuous, then it is continuous on every closed interval contained in its domain.
Intermediate Value Theorem
[edit | edit source]A useful theorem regarding continuous functions is the following:
If a function is continuous on a closed interval , then for every value between and there is a value such that .
Application: bisection method
[edit | edit source]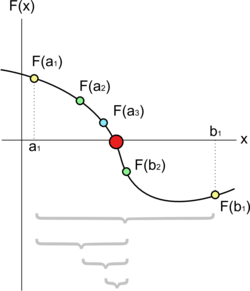
The bisection method is the simplest and most reliable algorithm to find zeros of a continuous function.
Suppose we want to solve the equation . Given two points and such that and have opposite signs, the intermediate value theorem tells us that must have at least one root between and as long as is continuous on the interval . If we know is continuous in general (say, because it's made out of rational, trigonometric, exponential and logarithmic functions), then this will work so long as is defined at all points between and . So, let's divide the interval in two by computing . There are now three possibilities:
- ,
- and have opposite signs, or
- and have opposite signs.
In the first case, we're done. In the second and third cases, we can repeat the process on the sub-interval where the sign change occurs. In this way we hone in to a small sub-interval containing the 0. The midpoint of that small sub-interval is usually taken as a good approximation to the 0.
Note that, unlike the methods you may have learned in algebra, this works for any continuous function that you (or your calculator) know how to compute.



























![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)







![{\displaystyle [a_{1},b_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90b50cd52227fb045ffb69b5802b79b7b539e8d2)


