Introduction to Artificial Neural Networks
| This is the print version of Artificial Neural Networks You won't see this message or any elements not part of the book's content when you print or preview this page. |
Artificial Neural Networks/Cover
Introduction
Introduction
Artificial neural networks are one of the most popular and promising areas of artificial intelligence research. Artificial Neural Networks are abstract computational models, roughly based on the organizational structure of the human brain. There are a wide variety of network architectures and learning methods that can be combined to produce neural networks with different computational abilities.
What is This Book About?
This book is going to serve as a general-purpose overview of artificial neural networks, including network construction, use, and applications.
Who is This Book For?
This book is going to be aimed at advanced undergraduates and graduate students in the areas of computer science, mathematics, engineering, and the sciences.
What Are The Prerequisites?
Readers of this book are going to require a solid mathematical background that includes, but may not be limited to:
Students may also find some benefit in the following engineering texts:
Students who wish to implement the lessons learned in this book should be familiar with at least one general-purpose programming language or have a background in:
Overview
Neural Network Basics
Artificial Neural Networks
Artificial Neural Networks, also known as “Artificial neural nets”, “neural nets”, or ANN for short, are a computational tool modeled on the interconnection of the neuron in the nervous systems of the human brain and that of other organisms. Biological Neural Nets (BNN) are the naturally occurring equivalent of the ANN. Both BNN and ANN are network systems constructed from atomic components known as “neurons”. Artificial neural networks are very different from biological networks, although many of the concepts and characteristics of biological systems are faithfully reproduced in the artificial systems. Artificial neural nets are a type of non-linear processing system that is ideally suited for a wide range of tasks, especially tasks where there is no existing algorithm for task completion. ANN can be trained to solve certain problems using a teaching method and sample data. In this way, identically constructed ANN can be used to perform different tasks depending on the training received. With proper training, ANN are capable of generalization, the ability to recognize similarities among different input patterns, especially patterns that have been corrupted by noise.
What Are Neural Nets?
The term “Neural Net” refers to both the biological and artificial variants, although typically the term is used to refer to artificial systems only. Mathematically, neural nets are nonlinear. Each layer represents a non-linear combination of non-linear functions from the previous layer. Each neuron is a multiple-input, multiple-output (MIMO) system that receives signals from the inputs, produces a resultant signal, and transmits that signal to all outputs. Practically, neurons in an ANN are arranged into layers. The first layer that interacts with the environment to receive input is known as the input layer. The final layer that interacts with the output to present the processed data is known as the output layer. Layers between the input and the output layer that do not have any interaction with the environment are known as hidden layers. Increasing the complexity of an ANN, and thus its computational capacity, requires the addition of more hidden layers, and more neurons per layer.
Biological neurons are connected in very complicated networks. Some regions of the human brain such as the cerebellum are composed of very regular patterns of neurons. Other regions of the brain, such as the cerebrum have less regular arrangements. A typical biological neural system has millions or billions of cells, each with thousands of interconnections with other neurons. Current artificial systems cannot achieve this level of complexity, and so cannot be used to reproduce the behavior of biological systems exactly.
Processing Elements
In an artificial neural network, neurons can take many forms and are typically referred to as Processing Elements (PE) to differentiate them from the biological equivalents. The PE are connected into a particular network pattern, with different patterns serving different functional purposes. Unlike biological neurons with chemical interconnections, the PE in artificial systems are electrical only, and may be either analog, digital, or a hybrid. However, to reproduce the effect of the synapse, the connections between PE are assigned multiplicative weights, which can be calibrated or “trained” to produce the proper system output.
McCulloch-Pitts Model
Processing Elements are typically defined in terms of two equations that represent the McCulloch-Pitts model of a neuron:
[McCulloch-Pitts Model]
Where ζ is the weighted sum of the inputs (the inner product of the input vector and the tap-weight vector), and σ(ζ) is a function of the weighted sum. If we recognize that the weight and input elements form vectors w and x, the ζ weighted sum becomes a simple dot product:

This may be called either the activation function (in the case of a threshold comparison) or a transfer function. The image to the right shows this relationship diagrammatically. The dotted line in the center of the neuron represents the division between the calculation of the input sum using the weight vector, and the calculation of the output value using the activation function. In an actual artificial neuron, this division may not be made explicitly.
The inputs to the network, x, come from an input space and the system outputs are part of the output space. For some networks, the output space Y may be as simple as {0, 1}, or it may be a complex multi-dimensional space. Neural networks tend to have one input per degree of freedom in the input space, and one output per degree of freedom in the output space.
The tap weight vector is updated during training by various algorithms. One of the more popular of which is the backpropagation algorithm which we will discuss in more detail later.
Why Use Neural Nets?
Artificial neural nets have a number of properties that make them an attractive alternative to traditional problem-solving techniques. The two main alternatives to using neural nets are to develop an algorithmic solution, and to use an expert system.
Algorithmic methods arise when there is sufficient information about the data and the underlying theory. By understanding the data and the theoretical relationship between the data, we can directly calculate unknown solutions from the problem space. Ordinary von Neumann computers can be used to calculate these relationships quickly and efficiently from a numerical algorithm.
Expert systems, by contrast, are used in situations where there is insufficient data and theoretical background to create any kind of a reliable problem model. In these cases, the knowledge and rationale of human experts is codified into an expert system. Expert systems emulate the deduction processes of a human expert, by collecting information and traversing the solution space in a directed manner. Expert systems are typically able to perform very well in the absence of an accurate problem model and complete data. However, where sufficient data or an algorithmic solution is available, expert systems are a less than ideal choice.
Artificial neural nets are useful for situations where there is an abundance of data, but little underlying theory. The data, which typically arises through extensive experimentation may be non-linear, non-stationary, or chaotic, and so may not be easily modeled. Input-output spaces may be so complex that a reasonable traversal with an expert system is not a satisfactory option. Importantly, neural nets do not require any a priori assumptions about the problem space, not even information about statistical distribution. Though such assumptions are not required, it has been found that the addition of such a priori information as the statistical distribution of the input space can help to speed training. Many mathematical problem models tend to assume that data lies in a standard distribution pattern, such as Gaussian or Maxwell-Boltzmann distributions. Neural networks require no such assumption. During training, the neural network performs the necessary analytical work, which would require non-trivial effort on the part of the analyst if other methods were to be used.
Learning
Learning is a fundamental component to an intelligent system, although a precise definition of learning is hard to produce. In terms of an artificial neural network, learning typically happens during a specific training phase. Once the network has been trained, it enters a production phase where it produces results independently. Training can take on many different forms, using a combination of learning paradigms, learning rules, and learning algorithms. A system which has distinct learning and production phases is known as a static network. Networks which are able to continue learning during production use are known as dynamical systems.
A learning paradigm is supervised, unsupervised or a hybrid of the two, and reflects the method in which training data is presented to the neural network. A method that combines supervised and unsupervised training is known as a hybrid method. A learning rule is a model for the types of methods to be used to train the system, and also a goal for what types of results are to be produced. The learning algorithm is the specific mathematical method that is used to update the inter-neuronal synaptic weights during each training iteration. Under each learning rule, there are a variety of possible learning algorithms for use. Most algorithms can only be used with a single learning rule. Learning rules and learning algorithms can typically be used with either supervised or unsupervised learning paradigms, however, and each will produce a different effect.
Overtraining is a problem that arises when too many training examples are provided, and the system becomes incapable of useful generalization. This can also occur when there are too many neurons in the network and the capacity for computation exceeds the dimensionality of the input space. During training, care must be taken not to provide too many input examples and different numbers of training examples could produce very different results in the quality and robustness of the network.
Network Parameters
There are a number of different parameters that must be decided upon when designing a neural network. Among these parameters are the number of layers, the number of neurons per layer, the number of training iterations, et cetera. Some of the more important parameters in terms of training and network capacity are the number of hidden neurons, the learning rate and the momentum parameter.
Number of neurons in the hidden layer
Hidden neurons are the neurons that are neither in the input layer nor the output layer. These neurons are essentially hidden from view, and their number and organization can typically be treated as a black box to people who are interfacing with the system. Using additional layers of hidden neurons enables greater processing power and system flexibility. This additional flexibility comes at the cost of additional complexity in the training algorithm. Having too many hidden neurons is analogous to a system of equations with more equations than there are free variables: the system is over specified, and is incapable of generalization. Having too few hidden neurons, conversely, can prevent the system from properly fitting the input data, and reduces the robustness of the system.


Data type: Integer Domain: [1, ∞) Typical value: 8
Meaning: Number of neurons in the hidden layer (additional layer to the input and output layers, not connected externally).
Learning Rate
Data type: Real Domain: [0, 1] Typical value: 0.3
Meaning: Learning Rate. Training parameter that controls the size of weight and bias changes in learning of the training algorithm.
Momentum
Data type: Real Domain: [0, 1] Typical value: 0.9
Meaning: Momentum simply adds a fraction m of the previous weight update to the current one. The momentum parameter is used to prevent the system from converging to a local minimum or saddle point. A high momentum parameter can also help to increase the speed of convergence of the system. However, setting the momentum parameter too high can create a risk of overshooting the minimum, which can cause the system to become unstable. A momentum coefficient that is too low cannot reliably avoid local minima, and can also slow down the training of the system.
Training type
Data type: Integer Domain: [0, 1] Typical value: 1
Meaning: 0 = train by epoch, 1 = train by minimum error
Epoch
Data type: Integer Domain: [1, ∞] Typical value: 5000000
Meaning: Determines when training will stop once the number of iterations exceeds epochs. When training by minimum error, this represents the maximum number of iterations.
Minimum Error
Data type: Real Domain: [0, 0.5] Typical value: 0.01
Meaning: Minimum mean square error of the epoch. Square root of the sum of squared differences between the network targets and actual outputs divided by number of patterns (only for training by minimum error).
Examples and realizations
- Repository on the github.
Biological Neural Networks
Biological Neural Nets
In the case of a biological neural net, neurons are living cells with axons and dendrites that form interconnections through electro-chemical synapses. Signals are transmitted through the cell body (soma), from the dendrite to the axon as an electrical impulse. In the pre-synaptic membrane of the axon, the electrical signal is converted into a chemical signal in the form of various neurotransmitters. These neurotransmitters, along with other chemicals present in the synapse form the message that is received by the post-synaptic membrane of the dendrite of the next cell, which in turn is converted to an electrical signal.
This page is going to provide a brief overview of biological neural networks, but the reader will have to find a better source for a more in-depth coverage of the subject.
Synapses

The figure above shows a model of the synapse showing the chemical messages of the synapse moving from the axon to the dendrite. Synapses are not simply a transmission medium for chemical signals, however. A synapse is capable of modifying itself based on the signal traffic that it receives. In this way, a synapse is able to “learn” from its past activity. This learning happens through the strengthening or weakening of the connection. External factors can also affect the chemical properties of the synapse, including body chemistry and medication.
Neurons
Cells have multiple dendrites, each receives a weighted input. Inputs are weighted by the strength of the synapse that the signal travels through. The total input to the cell is the sum of all such synaptic weighted inputs. Neurons utilize a threshold mechanism, so that signals below a certain threshold are ignored, but signals above the threshold cause the neuron to fire. Neurons follow an “all or nothing” firing scheme, and are similar in this respect to a digital component. Once a neuron has fired, a certain refraction period must pass before it can fire again.
Biological Networks
Biological neural systems are heterogeneous, in that there are many different types of cells with different characteristics. Biological systems are also characterized by macroscopic order, but nearly random interconnection on the microscopic layer. The random interconnection at the cellular level is rendered into a computational tool by the learning process of the synapse, and the formation of new synapses between nearby neurons.
History
Early History
The history of neural networking arguably started in the late 1800s with scientific attempts to study the workings of the human brain. In 1890, William James published the first work about brain activity patterns. In 1943, McCulloch and Pitts produced a model of the neuron that is still used today in artificial neural networking. This model is broken into two parts: a summation over weighted inputs and an output function of the sum.
Artificial Neural Networking
In 1949, Donald Hebb published The Organization of Behavior, which outlined a law for synaptic neuron learning. This law, later known as Hebbian Learning in honor of Donald Hebb is one of the simplest and most straight-forward learning rules for artificial neural networks.
In 1951, Marvin Minsky created the first ANN while working at Princeton.
In 1958 The Computer and the Brain was published posthumously, a year after John von Neumann’s death. In that book, von Neumann proposed many radical changes to the way in which researchers had been modeling the brain.
Mark I Perceptron
The Mark I Perceptron was also created in 1958, at Cornell University by Frank Rosenblatt. The Perceptron was an attempt to use neural network techniques for character recognition. The Mark I Perceptron was a linear system, and was useful for solving problems where the input classes were linearly separable in the input space. In 1960, Rosenblatt published the book Principles of Neurodynamics, containing much of his research and ideas about modeling the brain.
The Perceptron was a linear system with a simple input-output relationship defined as a McCulloch-Pitts neuron with a step activation function. In this model, the weighted inputs were compared to a threshold θ. The output, y, was defined as a simple step function:
Despite the early success of the Perceptron and artificial neural network research, there were many people who felt that there was limited promise in these techniques. Among these were Marvin Minsky and Seymore Papert, whose 1969 book Perceptrons was used to discredit ANN research and focus attention on the apparent limitations of ANN work. One of the limitations that Minsky and Papert pointed out most clearly was the fact that the Perceptron was not able to classify patterns that are not linearly separable in the input space. Below, the figure on the left shows an input space with a linearly separable classification problem. The figure on the right, in contrast, shows an input space where the classifications are not linearly separable.
 |
 |
Despite the failure of the Mark I Perceptron to handle non-linearly separable data, it was not an inherent failure of the technology, but a matter of scale. The Mark I was a two layer Perceptron, Hecht-Nielsen showed in 1990 that a three layer machine (multi layer Perceptron, or MLP) was capable of solving nonlinear separation problems. Perceptrons ushered in what some call the “quiet years”, where ANN research was at a minimum of interest. It wasn’t until the rediscovery of the backpropagation algorithm in 1986 that the field gained widespread interest again.
Backpropagation and Rebirth
The backpropagation algorithm, originally discovered by Werbos in 1974 was rediscovered in 1986 with the book Learning Internal Representation by Error Propagation by Rumelhart, Hinton and Williams. Backpropagation is a form of the gradient descent algorithm used with artificial neural networks for minimization and curve-fitting.
In 1987 the IEEE annual international ANN conference was started for ANN researchers. In 1987 the International Neural Network Society (INNS) was formed, along with the INNS Neural Networking journal in 1988.
MATLAB Neural Networking Toolbox
MATLAB
MATLAB ® is an ideal tool for working with artificial neural networks for a number of reasons. First, MATLAB is highly efficient in performing vector and matrix calculations. Second, MATLAB comes with a specialized Neural Network Toolbox ® which contains a number of useful tools for working with artificial neural networks.
This book is going to utilize the MATLAB programming environment and the Neural Network Toolbox to do examples and problems throughout the book.
Other Neural Network Software
Even though this book is going to focus on MATLAB for its problems and examples, there are a number of other tools that can be used for constructing, testing, and implementing neural networks. E.g.
Activation Functions
Activation Functions
There are a number of common activation functions in use with neural networks. This is not an exhaustive list.

Step Function
A step function is a function like that used by the original Perceptron. The output is a certain value, A1, if the input sum is above a certain threshold and A0 if the input sum is below a certain threshold. The values used by the Perceptron were A1 = 1 and A0 = 0.
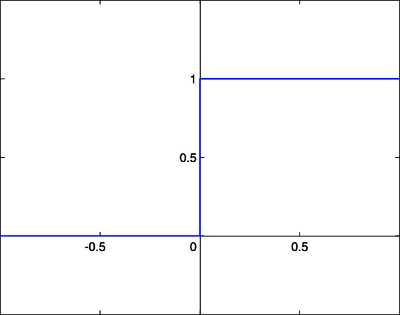
These kinds of step activation functions are useful for binary classification schemes. In other words, when we want to classify an input pattern into one of two groups, we can use a binary classifier with a step activation function. Another use for this would be to create a set of small feature identifiers. Each identifier would be a small network that would output a 1 if a particular input feature is present, and a 0 otherwise. Combining multiple feature detectors into a single network would allow a very complicated clustering or classification problem to be solved.
Linear combination
A linear combination is where the weighted sum input of the neuron plus a linearly dependent bias becomes the system output. Specifically:
In these cases, the sign of the output is considered to be equivalent to the 1 or 0 of the step function systems, which enables the two methods be to equivalent if
- .
Continuous Log-Sigmoid Function
A log-sigmoid function, also known as a logistic function, is given by the relationship:
Where β is a slope parameter. This is called the log-sigmoid because a sigmoid can also be constructed using the hyperbolic tangent function instead of this relation, in which case it would be called a tan-sigmoid. Here, we will refer to the log-sigmoid as simply “sigmoid”. The sigmoid has the property of being similar to the step function, but with the addition of a region of uncertainty. Sigmoid functions in this respect are very similar to the input-output relationships of biological neurons, although not exactly the same. Below is the graph of a sigmoid function.
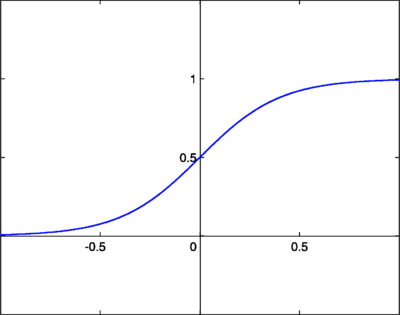
Sigmoid functions are also prized because their derivatives are easy to calculate, which is helpful for calculating the weight updates in certain training algorithms. The derivative when is given by:
When , using , the derivative is given by:
Continuous Tan-Sigmoid Function
Its derivative is:
ReLU: Rectified Linear Unit
The ReLU activation function is defined as:
It can also be expressed piecewise:

Its derivative is:
ReLU was first introduced by Kunihiko Fukushima in 1969 for representation learning with images, and is now the most popular activation function for deep learning. It has a very simple formula and derivative, making backpropagation calculations easier to calculate. As the output of the derivative function is always 1 for positive inputs, it suffers less from the gradient vanishing or exploding problem than other activation functions. ReLU does present the unique problem of "dying ReLU", where some nodes may very rarely activate or "die", providing no predictive power to the model. Variants of ReLU including Leaky and Parametric ReLU have been introduced to avoid the dying ReLU problem.
Softmax Function
The softmax activation function is useful predominantly in the output layer of a clustering system. Softmax functions convert a raw value into a posterior probability. This provides a measure of certainty. The softmax activation function is given as:
L is the set of neurons in the output layer.
ANN Models
Feed-Forward Networks
Feedforward Systems
Feed-forward neural networks are the simplest form of ANN. Shown below, a feed-forward neural net contains only forward paths. A Multilayer Perceptron (MLP) is an example of feed-forward neural networks. The following figure below show a feed-forward networks with two hidden layers.



Connection Weights
In a feed-forward system PE are arranged into distinct layers with each layer receiving input from the previous layer and outputting to the next layer. There is no feedback. This means that signals from one layer are not transmitted to a previous layer. This can be stated mathematically as:
Weights of direct feedback paths, from a neuron to itself, are zero. Weights from a neuron to a neuron in a previous layer are also zero. Notice that weights for the forward paths may also be zero depending on the specific network architecture, but they do not need to be. A network without all possible forward paths is known as a sparsely connected network, or a non-fully connected network. The percentage of available connections that are utilized is known as the connectivity of the network.
Mathematical Relationships
The weights from each neuron in layer l - 1 to the neurons in layer l are arranged into a matrix wl. Each column corresponds to a neuron in l - 1, and each row corresponds to a neuron in l. The input signal from l - 1 to l is the vector xl. If ρl is a vector of activation functions [σ1 σ2 … σn] that acts on each row of input and bl is an arbitrary offset vector (for generalization) then the total output of layer l is given as:
Two layers of output can be calculated by substituting the output from the first layer into the input of the second layer:
This method can be continued to calculate the output of a network with an arbitrary number of layers. Notice that as the number of layers increases, so does the complexity of this calculation. Sufficiently large neural networks can quickly become too complex for direct mathematical analysis.
Radial Basis Function Networks
In a radial basis function (RBF) networks are neural nets with three layers. The first input layer feeds data to a hidden intermediate layer. The hidden layer processes the data and transports it to the output layer. Only the tap weights between the hidden layer and the output layer are modified during training. Each hidden layer neuron represents a basis function of the output space, with respect to a particular center in the input space. The activation function chosen is commonly a Gaussian kernel:
This kernel is centered at the point in the input space specified by the weight vector. The closer the input signal is to the current weight vector, the higher the output of the neuron will be. Radial basis function networks are used commonly in function approximation and series prediction.
Recurrent Networks
Recurrent Networks
In a recurrent network, the weight matrix for each layer l contains input weights from all other neurons in the network, not just neurons from the previous layer. The additional complexity from these feedback paths can have a number of advantages and disadvantages in the network.
Simple Recurrent Networks
Recurrent networks, in contrast to feed-forward networks, do have feedback elements that enable signals from one layer to be fed back to a previous layer. A basic recurrent network is shown in figure 6. A simple recurrent network is one with three layers, an input, an output, and a hidden layer. A set of additional context units are added to the input layer that receive input from the hidden layer neurons. The feedback paths from the hidden layer to the context units have a fixed weight of unity.
A fully recurrent network is one where every neuron receives input from all other neurons in the system. Such networks cannot be easily arranged into layers. A small subset of neurons receives external input, and another small subset produce system output. A recurrent network is known as symmetrical network if:


Elman Network
An Elman Network is a special case of a Simple Recurrent Network (SRN) with four layers: An input layer, an output layer, a hidden layer and a context layer. The context layer feeds the hidden layer at iteration N with a value computed from the output of the hidden layer at iteration N-1, providing a short memory effect. Elman networks are used, for example, for predicting series of values.

Echo State Networks
Echo State Networks, part of the Reservoir Computing paradigm, are an efficient type of Recurrent Neural Network where the recurrent neurons only have a partial connectivity between themselves. Such networks where only a subset of all possible connections is made are known as sparsely connected networks. In Echo State Networks, only the weights from the hidden layer to the output layer may be altered during training.
Echo State Networks are useful for matching and reproducing specific input patterns. Since the only tap weights modified during training are the output layer tap weights, training is typically quick and computationally efficient in comparison to other multi-layer networks that are not sparsely connected.
Hopfield Networks
Hopfield Networks
Hopfield networks are one of the oldest and simplest networks. Hopfield networks utilize a network energy function. The activation function of a binary Hopfield network is given by the signum function of a biased weighted sum:
Hopfield networks are frequently binary-valued, although continuous variants do exist. Binary networks are useful for classification and clustering purposes.
Energy Function
The energy function for the network is given as:
Here, the y parameters are the outputs of the ith and jth units. During training the network energy should decrease until it reaches a minimum. This minimum is known as the attractor of the network. As a Hopfield network progresses, the energy minimizes itself. This means that mathematical minimization or optimization problems can be solved automatically by the Hopfield network if that problem can be formulated in terms of the network energy.
Associative Memory
Hopfield networks can be used as an associative memory network for data storage purposes. Each attractor represents a different data value that is stored in the network, and a range of associated patterns can be used to retrieve the data pattern. The number of distinct patterns p that can be stored in such a network is given approximately as:
Where n is the number of neurons in the network.
Self-Organizing Maps
Self-Organizing Maps
Self-organizing maps (SOM), sometimes called Kohonen SOM after their creator, are used with unsupervised learning. SOM are modeled on biological neural networks, where groups of neurons appear to self organize into specific regions with common functionality.
Neuron Regions
Different regions of the SOM network are trained to be detectors for distinct features from the input set. Initial network weights are either set randomly, or are based off the eigenvectors of the input space. The Euclidean distance from each input sample to the weight vector of each neuron is computed, and the neuron whose weight vector is most similar to the input is declared the best match unit (BMU). The update formula is given as:
Here, w is the weight vector at time n. α is a monotonically decreasing function that ensures the learning rate will decrease over time. x is the input vector, and Θ[j, n] is a measure of the distance between the BMU and neuron j at iteration n. As can be seen from this algorithm, the amount by which the neuron weight vectors change is based on the distance from the BMU, and the amount of time. Decreasing the potential for change over time helps to reduce volatility during training, and helps to ensure that the network converges.
Competitive Models
Competitive Networks
Competitive networks are networks where neurons compete with one another. The weight vector is treated as a "prototype", and is matched against the input vector. The "winner" of each training session is the neuron whose weight vector is most similar to the input vector.
An example of a competitive network is shown below.

ART Models
In adaptive resonance theory (ART) networks, an overabundance of neurons leads some neurons to be committed (active) and others to be uncommitted (inactive). The weight vector, also known as the prototype, is said to resonate with the input vector if the two are sufficiently similar. Weights are only updated if they are resonating in the current iteration. ART networks commit an uncommitted neuron when a new input pattern is detected that does not resonate with any of the existing committed neurons. ART networks are fully-connected networks, in that all possible connections are made between all nodes.
Boltzmann Machines
Boltzmann learning compares the input data distribution P with the output data distribution of the machine, Q [24]. The distance between these distributions is given by the Kullback-Leibler distance:
Where:
Here, pij is the probability that elements i and j will both be on when the system is in its training phase (positive phase), and qij is the probability that both elements i and j will be on during the production phase (negative phase). The probability that element j will be on, pi, is given by:
T is a scalar constant known as the temperature of the system. Boltzmann learning is very powerful, but the complexity of the algorithm increases exponentially as more neurons are added to the network. To reduce this effect, a restricted Boltzmann machine (RBM) can be used. The hidden nodes in an RBM are not interconnected as they are in regular Boltzmann networks. Once trained on a particular feature set, these RBM can be combined together into larger, more diverse machines.
Because Boltzmann machine weight updates only require looking at the expected distributions of surrounding neurons, it is a plausible model for how actual biological neural networks learn.
Committee of Machines
Artificial neural networks can have very different properties depending on how they are constructed and how they are trained. Even in the case where two networks are trained on the same set of input data, different training algorithms can produce different systems with different characteristics. By combining multiple ANN into a single system, a committee of machines is formed. The result of a committee system is a combination of the results of the various component systems. For instance, the most common answer among a discrete set of answers in the committee can be taken as the overall answer, or the average answer can be taken.
Committee of machines (COM) systems tend to be more robust then the individual component systems, but they can also lose some of the “expertise” of the individual systems when answers are averaged out.
Teaching and Learning
Learning Paradigms
Learning Paradigms
There are three different learning paradigms that can be used to train a neural network. Supervised and unsupervised learning are the most common, with hybrid approaches between the two becoming increasingly common as well.
Supervised Learning
Supervised learning is a technique where the input and expected output of the system are provided, and the ANN is used to model the relationship between the two. Given an input set x, and a corresponding output set y, an optimal rule is to be determined such that:
Here, e is an approximation error that needs to be minimized. The input values are provided to the network which produces a result. This result is compared to the desired result, and this error signal is used to update the network weight vectors. Supervised learning is useful when we want the network to reproduce the characteristics of a certain relationship
Unsupervised Learning
In unsupervised learning, the data and a cost function are provided that is a function of the system input and output. The ANN is trained to minimize the cost function by finding a suitable input-output relationship.
Given an input set x, and a cost function g(x, y) of the input and output sets, the goal is to minimize the cost function through a proper selection of f (the relationship between x, and y). At each training iteration, the trainer provides the input to the network, and the network produces a result. This result is put into the cost function, and the total cost is used to update the weights. Weights are continually updated until the system output produces a minimal cost. Unsupervised learning is useful in situations where a cost function is known, but a data set is not know that minimizes that cost function over a particular input space.
Error-Correction Learning
Error-Correction Learning
Error-Correction Learning, used with supervised learning, is the technique of comparing the system output to the desired output value, and using that error to direct the training. In the most direct route, the error values can be used to directly adjust the tap weights, using an algorithm such as the backpropagation algorithm. If the system output is y, and the desired system output is known to be d, the error signal can be defined as:
Error correction learning algorithms attempt to minimize this error signal at each training iteration. The most popular learning algorithm for use with error-correction learning is the backpropagation algorithm, discussed below.
Gradient Descent
The gradient descent algorithm is not specifically an ANN learning algorithm. It has a large variety of uses in various fields of science, engineering, and mathematics. However, we need to discuss the gradient descent algorithm in order to fully understand the backpropagation algorithm. The gradient descent algorithm is used to minimize an error function g(y), through the manipulation of a weight vector w. The cost function should be a linear combination of the weight vector and an input vector x. The algorithm is:
Here, η is known as the step-size parameter, and affects the rate of convergence of the algorithm. If the step size is too small, the algorithm will take a long time to converge. If the step size is too large the algorithm might oscillate or diverge.
The gradient descent algorithm works by taking the gradient of the weight space to find the path of steepest descent. By following the path of steepest descent at each iteration, we will either find a minimum, or the algorithm could diverge if the weight space is infinitely decreasing. When a minimum is found, there is no guarantee that it is a global minimum, however.
Backpropagation
The backpropagation algorithm, in combination with a supervised error-correction learning rule, is one of the most popular and robust tools in the training of artificial neural networks. Back propagation passes error signals backwards through the network during training to update the weights of the network. Because of this dependence on bidirectional data flow during training, backpropagation is not a plausible reproduction of biological learning mechanisms. When talking about backpropagation, it is useful to define the term interlayer to be a layer of neurons, and the corresponding input tap weights to that layer. We use a superscript to denote a specific interlayer, and a subscript to denote the specific neuron from within that layer. For instance:
- (1)
- (2)
Where xil-1 are the outputs from the previous interlayer (the inputs to the current interlayer), wijl is the tap weight from the i input from the previous interlayer to the j element of the current interlayer. Nl-1 is the total number of neurons in the previous interlayer.
The backpropagation algorithm specifies that the tap weights of the network are updated iteratively during training to approach the minimum of the error function. This is done through the following equation:
- (3)
- (3)
The relationship between this algorithm and the gradient descent algorithm should be immediately apparent. Here, η is known as the learning rate, not the step-size, because it affects the speed at which the system learns (converges). The parameter μ is known as the momentum parameter. The momentum parameter forces the search to take into account its movement from the previous iteration. By doing so, the system will tend to avoid local minima or saddle points, and approach the global minimum. We will discuss these terms in greater detail in the next section.
The parameter δ is what makes this algorithm a “back propagation” algorithm. We calculate it as follows:
- (4)
The δ function for each layer depends on the δ from the previous layer. For the special case of the output layer (the highest layer), we use this equation instead:
- (5)
In this way, the signals propagate backwards through the system from the output layer to the input layer. This is why the algorithm is called the backpropagation algorithm.
Log-Sigmoid Backpropagation
If we use log-sigmoid activation functions for our neurons, the derivatives simplify, and our backpropagation algorithm becomes:
For the output layer, and
for all the hidden inner layers. This property makes the sigmoid function desirable for systems with a limited ability to calculate derivatives.
Learning Rate
The learning rate is a common parameter in many of the learning algorithms, and affects the speed at which the ANN arrives at the minimum solution. In backpropagation, the learning rate is analogous to the step-size parameter from the gradient-descent algorithm. If the step-size is too high, the system will either oscillate about the true solution, or it will diverge completely. If the step-size is too low, the system will take a long time to converge on the final solution.
Momentum Parameter
The momentum parameter is used to prevent the system from converging to a local minimum or saddle point. A high momentum parameter can also help to increase the speed of convergence of the system. However, setting the momentum parameter too high can create a risk of overshooting the minimum, which can cause the system to become unstable. A momentum coefficient that is too low cannot reliably avoid local minima, and also can slow the training of the system.
Hebbian Learning
Hebbian Learning
Hebbian learning is one of the oldest learning algorithms, and is based in large part on the dynamics of biological systems. A synapse between two neurons is strengthened when the neurons on either side of the synapse (input and output) have highly correlated outputs. In essence, when an input neuron fires, if it frequently leads to the firing of the output neuron, the synapse is strengthened. Following the analogy to an artificial system, the tap weight is increased with high correlation between two sequential neurons.
Mathematical Formulation
Mathematically, we can describe Hebbian learning as:
Here, η is a learning rate coefficient, and and are, respectively, the outputs of the ith and jth elements at time step n.
Plausibility
The Hebbian learning algorithm is performed locally, and doesn’t take into account the overall system input-output characteristic. This makes it a plausible theory for biological learning methods, and also makes Hebbian learning processes ideal in VLSI hardware implementations where local signals are easier to obtain.
Competitive Learning
Competitive Learning
Competitive learning is a rule based on the idea that only one neuron from a given iteration in a given layer will fire at a time. Weights are adjusted such that only one neuron in a layer, for instance the output layer, fires. Competitive learning is useful for classification of input patterns into a discrete set of output classes. The “winner” of each iteration, element i* , is the element whose total weighted input is the largest. Using this notation, one example of a competitive learning rule can be defined mathematically as:
Linear Vector Quantization
In a learning vector quantization (LVQ) machine, the input values are compared to the weight vector of each neuron. Neurons who most closely match the input are known as the best match unit (BMU) of the system. The weight vector of the BMU and those of nearby neurons are adjusted to be closer to the input vector by a certain step size. Neurons become trained to be individual feature detectors, and a combination of feature detectors can be used to identify large classes of features from the input space. The LVQ algorithm is a simplified precursor to more advanced learning algorithms, such as the self-organizing map. LVQ training is a type of competitive learning rule.
Boltzmann Learning
Boltzmann learning is statistical in nature, and is derived from the field of thermodynamics. It is similar to error-correction learning and is used during supervised training. In this algorithm, the state of each individual neuron, in addition to the system output, are taken into account. In this respect, the Boltzmann learning rule is significantly slower than the error-correction learning rule. Neural networks that use Boltzmann learning are called Boltzmann machines.
Boltzmann learning is similar to an error-correction learning rule, in that an error signal is used to train the system in each iteration. However, instead of a direct difference between the result value and the desired value, we take the difference between the probability distributions of the system.
ART Learning
ART Learning
Adaptive Resonance Theory (ART) learning algorithms compare the weight vector, known as the prototype, to the current input vector to produce a distance, r. The distance is compared to a specified scalar, the vigilance parameter p. All output nodes start off in the uncommitted state. When a new input sequence is detected that does not resonate with any committed nodes, an uncommitted node is committed, and it’s prototype vector is set to the current input vector.
Self-Organizing Maps
Self-Organizing Maps
Self-organizing maps (SOM), sometimes called Kohonen SOM after their creator, are used with unsupervised learning. SOM are modeled on biological neural networks, where groups of neurons appear to self organize into specific regions with common functionality.
Neuron Regions
Different regions of the SOM network are trained to be detectors for distinct features from the input set. Initial network weights are either set randomly, or are based off the eigenvectors of the input space. The Euclidean distance from each input sample to the weight vector of each neuron is computed, and the neuron whose weight vector is most similar to the input is declared the best match unit (BMU). The update formula is given as:
Here, w is the weight vector at time n. α is a monotonically decreasing function that ensures the learning rate will decrease over time. x is the input vector, and Θ[j, n] is a measure of the distance between the BMU and neuron j at iteration n. As can be seen from this algorithm, the amount by which the neuron weight vectors change is based on the distance from the BMU, and the amount of time. Decreasing the potential for change over time helps to reduce volatility during training, and helps to ensure that the network converges.
Applications
Pattern Recognition
Artificial neural networks are useful for pattern matching applications. Pattern matching consists of the ability to identify the class of input signals or patterns. Pattern matching ANN are typically trained using supervised learning techniques. One application where artificial neural nets have been applied extensively is optical character recognition (OCR). OCR has been a very successful area of research involving artificial neural networks.
An example of a pattern matching neural network is that used by VISA for identifying suspicious transactions and fraudulent purchases. When input symbols do not match an accepted pattern, the system raises a warning flag that indicates a potential problem.
Clustering
Similar to pattern matching, clustering is the ability to associate similar input patterns together, based on a measurement of their similarity or dissimilarity. An example of a clustering problem is the Netflix Prize, a competition to improve the Netflix recommendation system. Competitors are attempting to produce software systems that can suggest movies based on movies the viewer has already rated. Essentially, clustering movies based on the predicted like or dislike of the viewer.
Feature Detection
Feature detection or “association” networks are trained using non-noisy data, in order to recognize similar patterns in noisy or incomplete data. Correctly detecting features in the presence of noise can be used as an important tool for noise reduction and filtering.
For example, neural nets have been used successfully in a number of medical applications for detection of disease. One particular example is the use of ANN to detect breast cancer in mammography images.
Series Prediction
ANN can be trained to match the statistical properties of a particular input signal, and can even be used to predict future values of time series. There are a number of applications of feature prediction that have received significant research attention. Among these are financial prediction, meteorological prediction, and electric load prediction. ANN have shown themselves to be very robust in predicting complicated series, including non-linear non-stationary chaotic systems.
Financial prediction is useful for anticipating events in the economic system, which is considered to be a chaotic system. ANN have been used to predict the performance and failure rate of companies, changes in the exchange rate, and other economic metrics.
Meteorological prediction is a difficult process because current atmospheric models rely on highly recursive sets of differential equations which can be difficult to calculate, and which propagate errors through the successive iterations. Using neural nets for meteorological prediction is a non-trivial task, and there have been many conflicting reports of the efficacy of the technique.
Data Compression
Artificial Neural Networks/Data Compression
Curve Fitting
Curve Fitting
Curve-fitting problems represent an attempt for the neural network to identify and approximate an arbitrary input-output relation. Once the relation has been modeled to the necessary accuracy by the network, it can be used for a variety of tasks, such as series prediction, function approximation, and function optimization.
Function Approximation
Function approximation or modeling is the act of training a neural network using a given set of input-output data (typically through supervised learning) in order to deduce the relationship between the input and the output. After training, such an ANN can be used as a black box with an input-output characteristic approximately equal to the relationship of the training problems. Because of the modular and non-linear nature of artificial neural nets, they are considered to be able to approximate any arbitrary function to an arbitrary degree of accuracy. More accuracy in this case represents a tradeoff with system complexity, and the ability to generalize.
Optimization
Optimization ANNs are concerned with the minimization of a particular cost function with respect to certain constraints. ANN are shown to be capable of highly efficient optimization.
Control
Control Systems
Artificial neural networks have been employed for use in control systems because of their ability to identify patterns, and to match arbitrary non-linear response curves.
See Also
Future Work
Criticisms and Problems
Artificial Neural Networks/Criticisms and Problems
Artificial Intelligence
Artificial Neural Networks/Artificial Intelligence
Resources
Resources
Wikibooks
- Artificial Intelligence
- Linear Algebra
- Abstract Algebra
- Calculus
- Signals and Systems
- Engineering Analysis
- MATLAB Programming
Commons
Licensing
License
The text of this book is released under the following license:
|
|
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled "GNU Free Documentation License." |
GNU Free Documentation License
As of July 15, 2009 Wikibooks has moved to a dual-licensing system that supersedes the previous GFDL only licensing. In short, this means that text licensed under the GFDL only can no longer be imported to Wikibooks, retroactive to 1 November 2008. Additionally, Wikibooks text might or might not now be exportable under the GFDL depending on whether or not any content was added and not removed since July 15. |
Version 1.3, 3 November 2008 Copyright (C) 2000, 2001, 2002, 2007, 2008 Free Software Foundation, Inc. <http://fsf.org/>
Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.
0. PREAMBLE
The purpose of this License is to make a manual, textbook, or other functional and useful document "free" in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.
This License is a kind of "copyleft", which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.
We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.
1. APPLICABILITY AND DEFINITIONS
This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions stated herein. The "Document", below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as "you". You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.
A "Modified Version" of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.
A "Secondary Section" is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document's overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.
The "Invariant Sections" are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.
The "Cover Texts" are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.
A "Transparent" copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not "Transparent" is called "Opaque".
Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript or PDF produced by some word processors for output purposes only.
The "Title Page" means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, "Title Page" means the text near the most prominent appearance of the work's title, preceding the beginning of the body of the text.
The "publisher" means any person or entity that distributes copies of the Document to the public.
A section "Entitled XYZ" means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as "Acknowledgements", "Dedications", "Endorsements", or "History".) To "Preserve the Title" of such a section when you modify the Document means that it remains a section "Entitled XYZ" according to this definition.
The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty Disclaimers may have is void and has no effect on the meaning of this License.
2. VERBATIM COPYING
You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.
You may also lend copies, under the same conditions stated above, and you may publicly display copies.
3. COPYING IN QUANTITY
If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document's license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.
If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.
If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.
It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.
4. MODIFICATIONS
You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:
- Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.
- List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release you from this requirement.
- State on the Title page the name of the publisher of the Modified Version, as the publisher.
- Preserve all the copyright notices of the Document.
- Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
- Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
- Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document's license notice.
- Include an unaltered copy of this License.
- Preserve the section Entitled "History", Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled "History" in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
- Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the "History" section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
- For any section Entitled "Acknowledgements" or "Dedications", Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
- Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
- Delete any section Entitled "Endorsements". Such a section may not be included in the Modified version.
- Do not retitle any existing section to be Entitled "Endorsements" or to conflict in title with any Invariant Section.
- Preserve any Warranty Disclaimers.
If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version's license notice. These titles must be distinct from any other section titles.
You may add a section Entitled "Endorsements", provided it contains nothing but endorsements of your Modified Version by various parties—for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.
You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.
The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.
5. COMBINING DOCUMENTS
You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.
The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.
In the combination, you must combine any sections Entitled "History" in the various original documents, forming one section Entitled "History"; likewise combine any sections Entitled "Acknowledgements", and any sections Entitled "Dedications". You must delete all sections Entitled "Endorsements".
6. COLLECTIONS OF DOCUMENTS
You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.
You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.
7. AGGREGATION WITH INDEPENDENT WORKS
A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an "aggregate" if the copyright resulting from the compilation is not used to limit the legal rights of the compilation's users beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.
If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document's Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.
8. TRANSLATION
Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.
If a section in the Document is Entitled "Acknowledgements", "Dedications", or "History", the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.
9. TERMINATION
You may not copy, modify, sublicense, or distribute the Document except as expressly provided under this License. Any attempt otherwise to copy, modify, sublicense, or distribute it is void, and will automatically terminate your rights under this License.
However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior to 60 days after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your receipt of the notice.
Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, receipt of a copy of some or all of the same material does not give you any rights to use it.
10. FUTURE REVISIONS OF THIS LICENSE
The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See http://www.gnu.org/copyleft/.
Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License "or any later version" applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation. If the Document specifies that a proxy can decide which future versions of this License can be used, that proxy's public statement of acceptance of a version permanently authorizes you to choose that version for the Document.
11. RELICENSING
"Massive Multiauthor Collaboration Site" (or "MMC Site") means any World Wide Web server that publishes copyrightable works and also provides prominent facilities for anybody to edit those works. A public wiki that anybody can edit is an example of such a server. A "Massive Multiauthor Collaboration" (or "MMC") contained in the site means any set of copyrightable works thus published on the MMC site.
"CC-BY-SA" means the Creative Commons Attribution-Share Alike 3.0 license published by Creative Commons Corporation, a not-for-profit corporation with a principal place of business in San Francisco, California, as well as future copyleft versions of that license published by that same organization.
"Incorporate" means to publish or republish a Document, in whole or in part, as part of another Document.
An MMC is "eligible for relicensing" if it is licensed under this License, and if all works that were first published under this License somewhere other than this MMC, and subsequently incorporated in whole or in part into the MMC, (1) had no cover texts or invariant sections, and (2) were thus incorporated prior to November 1, 2008.
The operator of an MMC Site may republish an MMC contained in the site under CC-BY-SA on the same site at any time before August 1, 2009, provided the MMC is eligible for relicensing.
How to use this License for your documents
To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:
- Copyright (c) YEAR YOUR NAME.
- Permission is granted to copy, distribute and/or modify this document
- under the terms of the GNU Free Documentation License, Version 1.3
- or any later version published by the Free Software Foundation;
- with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.
- A copy of the license is included in the section entitled "GNU
- Free Documentation License".
If you have Invariant Sections, Front-Cover Texts and Back-Cover Texts, replace the "with...Texts." line with this:
- with the Invariant Sections being LIST THEIR TITLES, with the
- Front-Cover Texts being LIST, and with the Back-Cover Texts being LIST.
If you have Invariant Sections without Cover Texts, or some other combination of the three, merge those two alternatives to suit the situation.
If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.








![{\displaystyle {\frac {d\sigma (t)}{dt}}=\sigma (t)[1-\sigma (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5cc22d67ef3f410413b2d68c6fb3091c06cc22)


![{\displaystyle {\frac {d\sigma (\beta ,t)}{dt}}=\beta [\sigma (\beta ,t)[1-\sigma (\beta ,t)]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a9a3b84b940e9843fbe5b55d281204acc91b6d3)















![{\displaystyle w_{j}[n+1]=w_{j}[n]+\Theta [j,n]\alpha [n](x[n]-w_{j}[n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89b5a1e02af265dc794187be6d7f1dff1c20b6ad)
![{\displaystyle w_{ij}[n+1]=w_{ij}[n]-{\frac {\partial G}{\partial w_{ij}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8dff57fd087a8e7357623661a3fbb0f2332c923)
![{\displaystyle {\frac {\partial G}{\partial w_{ij}}}=-{\frac {1}{T}}[p_{ij}-q_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07a401275a13b712bf52169a2b6c550e70695e43)



![{\displaystyle w_{ij}[n+1]=w_{ij}[n]+\eta g(w_{ij}[n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e79218d8297d93042a6536d6b589b7fc80347e62)


![{\displaystyle w_{ij}^{l}[n]=w_{ij}^{l}[n-1]+\delta w_{ij}^{l}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d96e21bd7033bb0a0a963abd3adc72de260778ce)
![{\displaystyle w_{ij}^{l-1}[n]=\eta \delta _{j}^{l}x_{i}^{l-1}[n]+\mu \Delta w_{ij}^{l}[n-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e25e7708a55147e192bdd2f51598f869f3ea287)




![{\displaystyle w_{ij}[n+1]=w_{ij}[n]+\eta x_{i}[n]x_{j}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/251c256db555ab331594cfa7caf8660c17e74470)
![{\displaystyle x_{i}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ae3a986c99fd36b6b09e7f31f46ab8369086f2f)
![{\displaystyle x_{j}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fcf8cd6500d65efb41e041f6e814a5e1515dc07)
![{\displaystyle w_{ij}[n+1]=w_{ij}[n]+\Delta w_{ij}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd1cfc717a2b041775b12b5dcb4b75e577186ffc)
