Algorithms/Hill Climbing
Top, Chapters: 1, 2, 3, 4, 5, 6, 7, 8, 9, A
Hill climbing is a technique for certain classes of optimization problems. The idea is to start with a sub-optimal solution to a problem (i.e., start at the base of a hill) and then repeatedly improve the solution (walk up the hill) until some condition is maximized (the top of the hill is reached).
Hill-Climbing Methodology
|
One of the most popular hill-climbing problems is the network flow problem. Although network flow may sound somewhat specific it is important because it has high expressive power: for example, many algorithmic problems encountered in practice can actually be considered special cases of network flow. After covering a simple example of the hill-climbing approach for a numerical problem we cover network flow and then present examples of applications of network flow.
Newton's Root Finding Method
[edit | edit source]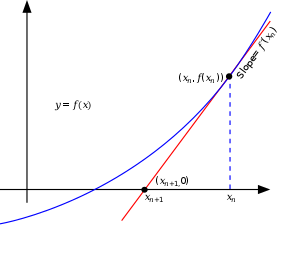
Newton's Root Finding Method is a three-centuries-old algorithm for finding numerical approximations to roots of a function (that is a point where the function becomes zero), starting from an initial guess. You need to know the function and its first derivative for this algorithm. The idea is the following: In the vicinity of the initial guess we can form the Taylor expansion of the function
which gives a good approximation to the function near . Taking only the first two terms on the right hand side, setting them equal to zero, and solving for , we obtain
which we can use to construct a better solution
This new solution can be the starting point for applying the same procedure again. Thus, in general a better approximation can be constructed by repeatedly applying
As shown in the illustration, this is nothing else but the construction of the zero from the tangent at the initial guessing point. In general, Newton's root finding method converges quadratically, except when the first derivative of the solution vanishes at the root.
Coming back to the "Hill climbing" analogy, we could apply Newton's root finding method not to the function , but to its first derivative , that is look for such that . This would give the extremal positions of the function, its maxima and minima. Starting Newton's method close enough to a maximum this way, we climb the hill.
Example application of Newton's method
[edit | edit source]The net present value function is a function of time, an interest rate, and a series of cash flows. A related function is Internal Rate of Return. The formula for each period is (CFi x (1+ i/100) t , and this will give a polynomial function which is the total cash flow, and equals zero when the interest rate equals the IRR. In using Newton's method, x is the interest rate, and y is the total cash flow, and the method will use the derivative function of the polynomial to find the slope of the graph at a given interest rate (x-value), which will give the xn+1 , or a better interest rate to try in the next iteration to find the target x where y ( the total returns) is zero.
Instead of regarding continuous functions, the hill-climbing method can also be applied to discrete networks.
Network Flow
[edit | edit source]Suppose you have a directed graph (possibly with cycles) with one vertex labeled as the source and another vertex labeled as the destination or the "sink". The source vertex only has edges coming out of it, with no edges going into it. Similarly, the destination vertex only has edges going into it, with no edges coming out of it. We can assume that the graph is fully connected with no dead-ends; i.e., for every vertex (except the source and the sink), there is at least one edge going into the vertex and one edge going out of it.
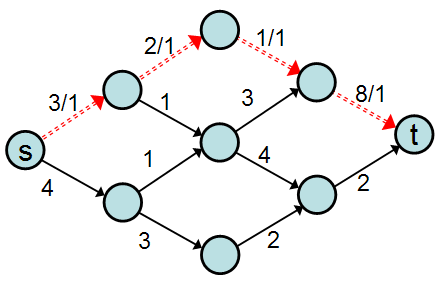
We assign a "capacity" to each edge, and initially we'll consider only integral-valued capacities. The following graph meets our requirements, where "s" is the source and "t" is the destination:
We'd like now to imagine that we have some series of inputs arriving at the source that we want to carry on the edges over to the sink. The number of units we can send on an edge at a time must be less than or equal to the edge's capacity. You can think of the vertices as cities and the edges as roads between the cities and we want to send as many cars from the source city to the destination city as possible. The constraint is that we cannot send more cars down a road than its capacity can handle.
The goal of network flow is to send as much traffic from to as each street can bear.
To organize the traffic routes, we can build a list of different paths from city to city . Each path has a carrying capacity equal to the smallest capacity value for any edge on the path; for example, consider the following path :
Even though the final edge of has a capacity of 8, that edge only has one car traveling on it because the edge before it only has a capacity of 1 (thus, that edge is at full capacity). After using this path, we can compute the residual graph by subtracting 1 from the capacity of each edge:
(We subtracted 1 from the capacity of each edge in because 1 was the carrying capacity of .) We can say that path has a flow of 1. Formally, a flow is an assignment of values to the set of edges in the graph such that:
- 1.
- 2.
- 3.
- 4.
Where is the source node and is the sink node, and is the capacity of edge . We define the value of a flow to be:
The goal of network flow is to find an such that is maximal. To be maximal means that there is no other flow assignment that obeys the constraints 1-4 that would have a higher value. The traffic example can describe what the four flow constraints mean:
- . This rule simply defines a flow to be a function from edges in the graph to real numbers. The function is defined for every edge in the graph. You could also consider the "function" to simply be a mapping: Every edge can be an index into an array and the value of the array at an edge is the value of the flow function at that edge.
- . This rule says that if there is some traffic flowing from node u to node v then there should be considered negative that amount flowing from v to u. For example, if two cars are flowing from city u to city v, then negative two cars are going in the other direction. Similarly, if three cars are going from city u to city v and two cars are going city v to city u then the net effect is the same as if one car was going from city u to city v and no cars are going from city v to city u.
- . This rule says that the net flow (except for the source and the destination) should be neutral. That is, you won't ever have more cars going into a city than you would have coming out of the city. New cars can only come from the source, and cars can only be stored in the destination. Similarly, whatever flows out of s must eventually flow into t. Note that if a city has three cars coming into it, it could send two cars to one city and the remaining car to a different city. Also, a city might have cars coming into it from multiple sources (although all are ultimately from city s).
- .
The Ford-Fulkerson Algorithm
[edit | edit source]The following algorithm computes the maximal flow for a given graph with non-negative capacities. What the algorithm does can be easy to understand, but it's non-trivial to show that it terminates and provides an optimal solution.
function net-flow(graph (V, E), node s, node t, cost c): flow
initialize f(e) := 0 for all e in E
loop while not done
for all e in E: // compute residual capacities
let cf(e) := c(e) - f(e)
repeat
let Gf := (V, {e : e in E and cf(e) > 0})
find a path p from s to t in Gf // e.g., use depth first search
if no path p exists: signal done
let path-capacities := map(p, cf) // a path is a set of edges
let m := min-val-of(path-capacities) // smallest residual capacity of p
for all (u, v) in p: // maintain flow constraints
f((u, v)) := f((u, v)) + m
f((v, u)) := f((v, u)) - m
repeat
repeat
end
The Ford-Fulkerson algorithm uses repeated calls to Breadth-First Search ( use a queue to schedule the children of a node to become the current node). Breadth-First Search increments the length of each path +1 so that the first path to get to the destination, the shortest path, will be the first off the queue. This is in contrast with using a Stack, which is Depth-First Search, and will come up with *any* path to the target, with the "descendants" of current node examined, but not necessarily the shortest.
- In one search, a path from source to target is found. All nodes are made unmarked at the beginning of a new search. Seen nodes are "marked" , and not searched again if encountered again. Eventually, all reachable nodes will have been scheduled on the queue , and no more unmarked nodes can be reached off the last the node on the queue.
- During the search, nodes scheduled have the finding "edge" (consisting of the current node , the found node, a current flow, and a total capacity in the direction first to second node), recorded.
- This allows finding a reverse path from the target node once reached, to the start node. Once a path is found, the edges are examined to find the edge with the minimum remaining capacity, and this becomes the flow that will result along this path , and this quantity is removed from the remaining capacity of each edge along the path. At the "bottleneck" edge with the minimum remaining capacity, no more flow will be possible, in the forward direction, but still possible in the backward direction.
- This process of BFS for a path to the target node, filling up the path to the bottleneck edge's residual capacity, is repeated, until BFS cannot find a path to the target node ( the node is not reached because all sequences of edges leading to the target have had their bottleneck edges filled). Hence memory of the side effects of previous paths found, is recorded in the flows of the edges, and affect the results of future searches.
- An important property of maximal flow is that flow can occur in the backward direction of an edge, and the residual capacity in the backward direction is the current flow in the foward direction. Normally, the residual capacity in the forward direction of an edge is the initial capacity less forward flow. Intuitively, this allows more options for maximizing flow as earlier augmenting paths block off shorter paths.
- On termination, the algorithm will retain the marked and unmarked states of the results of the last BFS.
- the minimum cut state is the two sets of marked and unmarked nodes formed from the last unsuccessful BFS starting from the start node, and not marking the target the node. The start node belongs to one side of the cut, and the target node belongs to the other. Arbitrarily, being "in Cut" means being on the start side, or being a marked node. Recall how are a node comes to be marked, given an edge with a flow and a residual capacity.
Example application of Ford-Fulkerson maximum flow/ minimum cut
[edit | edit source]An example of application of Ford-Fulkerson is in baseball season elimination. The question is whether the team can possibly win the whole season by exceeding some combination of wins of the other teams.
The idea is that a flow graph is set up with teams not being able to exceed the number of total wins which a target team can maximally win for the entire season. There are game nodes whose edges represent the number of remaining matches between two teams, and each game node outflows to two team nodes, via edges that will not limit forward flow; team nodes receive edges from all games they participate. Then outflow edges with win limiting capacity flow to the virtual target node. In a maximal flow state where the target node's total wins will exceed some combination of wins of the other teams, the penultimate depth-first search will cutoff the start node from the rest of the graph, because no flow will be possible to any of the game nodes, as a result of the penultimate depth-first search (recall what happens to the flow , in the second part of the algorithm after finding the path). This is because in seeking the maximal flow of each path, the game edges' capacities will be maximally drained by the win-limit edges further along the path, and any residual game capacity means there are more games to be played that will make at least one team overtake the target teams' maximal wins. If a team node is in the minimum cut, then there is an edge with residual capacity leading to the team, which means what , given the previous statements? What do the set of teams found in a minimum cut represent ( hint: consider the game node edge) ?
Example Maximum bipartite matching ( intern matching )
[edit | edit source]This matching problem doesn't include preference weightings. A set of companies offers jobs which are made into one big set , and interns apply to companies for specific jobs. The applications are edges with a weight of 1. To convert the bipartite matching problem to a maximum flow problem, virtual vertexes s and t are created , which have weighted 1 edges from s to all interns, and from all jobs to t. Then the Ford-Fulkerson algorithm is used to sequentially saturate 1 capacity edges from the graph, by augmenting found paths. It may happen that a intermediate state is reached where left over interns and jobs are unmatched, but backtracking along reverse edges which have residual capacity = forward flow = 1, along longer paths that occur later during breadth-first search, will negate previous suboptimal augmenting paths, and provide further search options for matching, and will terminate only when maximal flow or maximum matching is reached.
Top,