Abstract Algebra/Group Theory/Group/Double Inverse
Theorem
[edit | edit source]Let G be any group with operation .
- In Group G, inverse of inverse of any element g is g.
Proof
[edit | edit source]0. Choose 1. definition of inverse of g in G (usage 1,3) 2. let a = g−1 3. 4. definition of inverse of a in G (usage 2) 5. as a = g−1
Diagrams
[edit | edit source]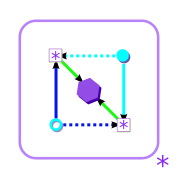 |
 |

![{\displaystyle \forall \;g\in G:[g^{-1}]^{-1}=g}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8555587cc09246a0f7fa57da9375a49abcfca1fd)




![{\displaystyle [{\color {BrickRed}a}]^{-1}={\color {OliveGreen}g}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa9a65da8c1a0633f148e0358fb165ecf145294e)
![{\displaystyle [{\color {BrickRed}g^{-1}}]^{-1}={\color {OliveGreen}g}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/776d9993a73e47a7736c36554797574b787a34aa)