A-level Mathematics/OCR/C1/Error bounds and Inequalities
Sometimes you won't be able to find an exact answer, but only an estimate of where the answer lies. This answer, along with suitable error bounds, are perfectly acceptable and are often used for experimental data when a high degree of accuracy isn't always justifiable.
Errors
[edit | edit source]If you were told that a certain door was 2 metres tall, you could assume that the door could be anywhere between 1.5 and 2.5 metres, represented by the inequality , and was actually rounded to 2 metres. If you were told that the same door is 2.0 metres, then you could assume more accuracy, and say the door was anywhere between 1.95 and 2.05 metres, represented by the inequality . Here you would say that the height of the door is 2 metres with error bounds of . This means that the actual value is within the range of 0.05m greater or less than the stated value. If you are not given error bounds of a measurement, you should assume that the last digit was rounded, and take all of the other digits as accurate.
The minimum and maximum value for the actual height of the door are called the lower and upper bounds, and are used to determine the accuracy of measurements.
Absolute error
[edit | edit source]The absolute error is the difference between the value that is obtained and the true value. The absolute error of a measurement can be found by using the following formula:
Relative error
[edit | edit source]The relative error is the absolute error as a proportion of the true value. The relative error of a measurement can be found by using the following formula:
Percentage error
[edit | edit source]The percentage error is the absolute error as a percentage of the true value. The percentage error of a measurement can be found by using the following formula:
For example, if the true value of the 2 metre door was 1.95 metres, the absolute error is , the relative error is , and the percentage error is .
Inequalities
[edit | edit source]An inequality is an expression which compares the relative sizes of points, lines, or curves. Unlike an equation, where both sides of the equals sign are always equal, inequalities can have one side greater than or equal to the other side.
The four signs of inequalities
[edit | edit source]There are four main basic signs:
- less than,
- greater than,
- less than or equal to, and
- greater than or equal to.
For example, means that is less than 4, means that is greater than 4, means that is four or any number less than this, and means that is four or any number higher than this.
Note that and are both essentially the same statement.
If you become confused with which sign means less than and greater than, it is useful to remember that the inequality signs always point to the smaller number. One basic rule to remember is that if you divide or multiply by a negative quantity the inequality sign reverses. For example will become . This makes sense because -4 is greater than -5 and 5 is greater than 4.
Combining inequalities
[edit | edit source]There are some cases where two inequalities can be combined into one. For example, the height of the door was said to be between and . The usual way of writing these is . Notice that the inequality signs are in the same direction. is perfectly acceptable, but it is incorrect to combine opposite facing inequalities and they must be left as two separate inequalities.
Solving Linear Inequalities
[edit | edit source]In order to solve a linear inequality simply isolate x. For example:
Note the sign change.
Solving Quadratic Inequalities
[edit | edit source]In order to solve a quadratic inequalities we need to: 1)Set the inequality to zero.
2)Factor the equation and find the zero(s).
3)Make a number line with the zero(s) of the equation as the only points. Make intervals between these points.
4)Find the sign of the factors. Then find the sign of the equation on the interval.
5)The interval(s) that satisfy the inequality is your answer set.
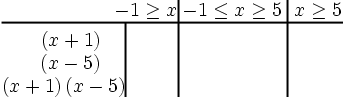
For example: Find the intervals that satisfy the relationship.
Step 1:
Step2: so the zeros will be -1 and 5
Step 3:
Edit: New pic needed to show the middle column as: x greater than or equal to -1 and less than or equal to 5.
Step 5: The intervals that satisfy the relationship are and .This is the solution set.
Solving Inequalities involving Fractions
[edit | edit source]Solving an equation involving a fraction is very similar to solving a quadratic inequalities. When you solve an inequality involving fractions you cannot cross multiply (because you could be multiplying by a negative number which would reverse the sign of the inequality). This will lead to an erroneous answer. Also remember that you can never have a zero in the denominator.
For example: Find the intervals that satisfy the relationship.
Step 1: then simplified it becomes .
Step 2: It is already factored so the zeros are -1 and 5.
Step 5: The intervals that satisfy the relationship are and therefore . Note that is greater than because x cannot equal -1 or else there will be a zero in the denominator.
Interval Notation
[edit | edit source]Interval notation is another way to write the interval of the solution to an inequality problem. You should give your answer in interval notation because it is easier to comprehend. In interval notation the solution set is given in brackets. There are two types of brackets that are used:
( ) This kind of bracket means that the endpoint is not included in the solution set. And
[ ] This kind on bracket means that the endpoint is included in the solution set. And
Also you can use various combinations of these brackets. If you have multiple intervals you will need to use the mathematical union sign . Also if you have an interval that goes to you need to use the round bracket ), because is a concept and not a number.
For example convert to interval notation:
In interval notation the solution set becomes , as you can see this is easier to comprehend.
This is part of the C1 (Core Mathematics 1) module of the A-level Mathematics text.














































![{\displaystyle \left(-\infty ,-4\right)\cup \left[-3,7\right)\cup \left(8,9\right]\cup \left[12,\infty \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5d111db3b2d335b733e41291e8825ab741bc9ea)