A-level Mathematics/OCR/C1/Coordinate Geometry and Graphs
Co-ordinates are a way of describing position. In two dimensions, positions are given in two perpendicular directions, x and y.
Linear Equations
[edit | edit source]Straight lines
[edit | edit source]A straight line has a fixed gradient. The gradient of a line and its y intercept are the two pieces of information that distinguish one line from another line.
Equations of a straight line
[edit | edit source]The most common form of a straight line is y = mx + c. m is the gradient of the line, and c is the point at which the line intercepts the y-axis. When c is 0, the line passes through the origin (0,0). Other forms of the equation are x = a, used for vertical lines of an infinite gradient and y = b is used for horizontal lines with a zero gradient. Also some equations are commonly written as: px + qy + c = 0. You can also use the equation y-y1=m(x-x1)
Gradient of a line
[edit | edit source]The steepness of a line can be measured by its gradient, which is the change in the y direction divided by the change in the x direction. The letter m is used to denote the gradient. The formula to find a gradient is: As a side note .
Point-Gradient Form
[edit | edit source]The equation of a line having the co-ordinate and having a gradient of m is: . Then you simply rearrange the equation into the form y = mx + c.
Parallel lines
[edit | edit source]A pair of lines are parallel (the symbol is ). If their gradients are equal, . So in order to find the equation of a parallel line you need the slope of the original line and one set of co-ordinates on the parallel line. Then you use the Point-Gradient formula to find the equation of the parallel line.
Perpendicular lines
[edit | edit source]A pair of lines are perpendicular (the symbol is ) if the product of their gradients is , . So if you need the equation of a line perpendicular to another line, all you need to do is replace the gradient m with the negative reciprocal of m.
So for example if line 1 is y = 2x +3 and you need to find the line perpendicular to this that goes through the point (0,1), then the gradient m = -1/2 (because 2 x -1/2 = -1).
This gives y = -x/2 +c.
Putting the known point (0,1) into this equation gives :
1= -0/2 +c which gives c = 1
so the equation is y = 1- x/2.
Distance between two points
[edit | edit source]Using the co-ordinates of two points, it is possible to calculate the distance between them using Pythagoras' theorem. The distance d between any two points and is given by:
Mid-point of a line
[edit | edit source]When the co-ordinate of two points are known, the mid-point is the point halfway between those two points. For any two points A and B, the co-ordinates of the mid-point of AB can be found by .
Intersection of lines
[edit | edit source]Any two straight lines will meet at a point, as long as they are not parallel. You can find the point of intersection simply by solving the two equations simultaneously. This is also true for curves, although non linear curves may intersect at multiple points or not at all and usually require different methods to solve.
Curves
[edit | edit source]To sketch a graph of a curve, all you need to know is the general shape of the curve and other important pieces of information such as the x and y intercepts and the points of any maxima and minima.
Curves in the form
[edit | edit source] |

|
| Degree 0 - Constant - or . In this case y=2 | Degree 1 - Linear - or . In this case y = x. |
 |
|
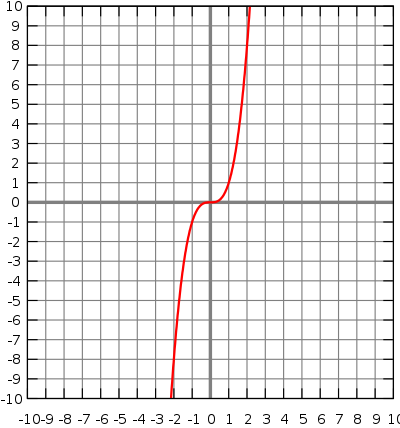
| Degree 2 - Quadratic - . In this case y = | Degree 3 - Cubic - . In this case y = |
Note: That all the odd powers of share the same general shape, moving from bottom-left to top-right, and that all the even powers of share the same "bucket" shaped curve.
Curves in the form
[edit | edit source]Just like earlier, curves with an even powers of all have the same general shape, and those with odd powers of share another general shape.
 |

|
 |

|
All curves in this form do not have a value for , because is undefined. There are asymptotes on the axis, where the curve moves towards the y axis increasingly slowly but will never actually touch.
Curves in the form
[edit | edit source]All curves in this form will not have values for x < 0. They will all have the same general shape.
Intersection of lines and curves
[edit | edit source]When a line intersects with a curve, it is possible to find the points of intersection by substituting the equation of the line into the equation of the curve. If the line is in the form , then you can replace any instances of with , and then expand the equation out and then factorise the resulting quadratic.
Need information on describing the geometrical relationship between a curve and a straight line
Intersection of curves
[edit | edit source]The same method can be used as for a line and a curve. However, it will only work in simple cases. When an algebraic method fails, you will need to resort to a graphical or Numerical Method. In the exam, you will only be required to use algebraic methods.
Graphical Rules
[edit | edit source]In many cases it is easy to obtain a graph from a preexisting graph using these rules.
Reflection
[edit | edit source]- is a reflection of through the x axis.
- is a reflection of through the y axis.
Stretching
[edit | edit source]- is stretched away from the y-axis if and stretched towards the y-axis if . In both cases the change is by b units.
- is stretched towards the x-axis if and stretched away from the x-axis if . In both cases the change is by a units.
Translations
[edit | edit source]- is a translation of f(x) by h units to the right.
- is a translation of f(x) by h units to the left.
- is a translation of f(x) by k units upwards.
- is a translation of f(x) by k units downwards.
The Circle
[edit | edit source]A circle is a set of all points in a plane that are a fixed distance r away from a given point called the center. The distance r is the radius of a circle.
The two basic laws of circles are:
Properties of a circle
[edit | edit source]A radius always bisects a chord if they are perpendicular to each other.
If any point on the circumference of the circle is connected to the diameter, it forms a right angled triangle.
If a radius is drawn and then a tangent is drawn from that point. Then the radius and tangent line will be perpendicular to each other.
Equation of a Circle
[edit | edit source]The standard equation of a circle is:
This will always give us a circle centered around the origin (0,0). If we want a circle with a center at (h,k) we use the following formula.
However you can not graph either of these equations with a calculator. You will need to split it into two equations, but the graph will not be perfect, because x is undefined when x = 0 and when : and .
Here is how would look graphed:
This is part of the C1 (Core Mathematics 1) module of the A-level Mathematics text.


























































