Unit 1.4.2 Data Structures
Structures
[edit | edit source]Record
[edit | edit source]An unordered data structure, with elements accessed via an attribute name. This makes the structure more user friendly as the attribute name describes the data stored.
All attributes must be defined before the record can be used. This makes initialization of the structure more complicated.
| first_name | last_name | |
|---|---|---|
| John | Smith | john.smith@example.com |
person.first_name // John person.email // john.smith@example.com
List
[edit | edit source]An ordered data structure, with element accessed via an index.
| 0 | 1 | 2 |
|---|---|---|
| 0048_jsmith | 0064_jbloggs | 0073_jdoe |
employee_ids[0] // 0048_jsmith employee_ids[2] // 0073_jdoe
Tuple
[edit | edit source]A list which is immutable (the data stored cannot be modified).
Useful for cases where the data needs to remain unchanged but accessible via an index.
Linked List
[edit | edit source]
A linked list is a list of data stored with pointers to the next item in the list. The last item in the list has a pointer of 0 or null marking it as the end of the list.
In addition to being dynamic, the main advantage of a linked list is that elements can be inserted at any point efficiently - only a few pointers need to be changed.
Here is an example of a linked list represented in a table: The names point to the next person in the alphabet.
start = 3 //Shows that the linked list starts at 3 (as A is at the start of the alphabet)
nextFree = 4 //Shows an available space where the next item to be added
| index | name | pointer |
|---|---|---|
| 0 | Lain | 2 |
| 1 | JoJo | 0 |
| 2 | Miku | null |
| 3 | Ash | 1 |
| 4 | null |
Suppose we want to insert Mikasa into the linked list:
- We would first place Mikasa in the space given by the nextFree pointer.
- We would next work out where we wanted Mikasa in the list. As we decided to link to the next item in the alphabet, Mikasa will come before Miku but after Lain. Therefore, Mikasa needs to be the 4th item in the list. eg.insert(3, "Mikasa") //3 refers to the 4th position as linked lists start at 0
- Lains pointer is changed to point at Mikasa (set to 4)
- Mikasa's pointer is set to point at Miku (set to 2)
- Finally the nextFree pointer would be set to 5 (the next free location)
Therefore the updated linked list would look like:
start = 3 //Shows that the linked list starts at 3 (as A is at the start of the alphabet)
nextFree = 5 //Shows an avaible space where the next item to be added
| index | name | pointer |
|---|---|---|
| 0 | Lain | |
| 1 | JoJo | 0 |
| 2 | Miku | null |
| 3 | Ash | 1 |
| 4 | Mikasa | |
| 5 | null |
Possible uses for a linked list:
- Implementing Undo functionality
- Dealing with Browser Cache
- Helping with operating system job queues
Describe a difference between an array and a linked list. [2]
Answer:
A linked list is a dynamic data structure (1) whereas an array is static (1). An array can have any element accessed directly (i.e. random access) (1) whereas a linked list needs to be traversed until the desired element is found (1). Contents of an array are stored contiguously in memory (1) whereas the contents of a linked list may not be (1).
Array
[edit | edit source]An array is an ordered data structure that is accessed through an index. It contains a group of elements which are usually of the same type. It is therefore a composite type as it forms a data structure out of pre-existing data types. By default, arrays require their size to be specified when they are defined and this is the number of elements within it. No elements can be added to an index beyond this size. This is adhered to in the majority of programming languages but some languages (namely Python and JavaScript are exceptions as they use a list as the underlying data structure for all defined arrays) break the rules.
One-dimensional arrays
[edit | edit source]One dimensional arrays contain a single group of properties with each being accessed by its index. This are almost approximate to a list, only differing in their fixed size.
| 0 | 1 | 2 |
|---|---|---|
| 0048_jsmith | 0064_jbloggs | 0073_jdoe |
employee_ids[0] // 0048_jsmith employee_ids[2] // 0073_jdoe
Multi-dimensional arrays
[edit | edit source]While arrays can be defined as a single dimension and hold a set of values as shown previously, they can also be declared as a multi-dimensional array. This means that each index of the array holds another array to the number of dimensions defined. This means that in a 2D array (as shown below) the array would be an array of arrays which would then all contain values. These can be used to store tabular data or data which should be accessed through an x and y coordinate such as pixels or tiles in a game.
These arrays can be incredibly useful to store more complex data but also require more complex programming to accommodate as you must understand exactly how the array is structures in order to access the correct data.
| shopSales[] | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 128.90 | 135.52 | 145.31 | 156.65 |
| 1 | 50.11 | 30.34 | 40.32 | 45.43 |
| 2 | 67.54 | 142.81 | 76.51 | 130.72 |
| 3 | 156.14 | 135.41 | 91.25 | 109.49 |
In the example above, shopSales could refer to how much profit was made by a chain of stores with the top index being the quarter and the left index being the shop number. It is worth noting that in many examples, you would need to access the top index first as that would contain the array for the shops themselves. However, this depends on how you initialise and define the array Eg:
let shopSales [4][4] = [
[128.90, 50.11, 67.54, 156.13],
[135.52, 30.34, 142.81, 135.41],
[145.31, 40.32, 76.51, 91.25],
[156.65, 45.43, 130.72, 109.49]
];
let cheltenham = 0;
let gloucester = 1;
let bristol = 2;
let london = 3;
shopSales[0][cheltenham]; //128.90 - The sales made in the Cheltenham store in the first quarter.
shopSales[3][london]; // 109.49 - The sales made in the London tore in the fourth quarter.
shopSales[2][1] // 40.32 - Gloucester store, second quarter
Stack
[edit | edit source]A stack is a modified implementation of a list. The data structure has a set of rules to follow when it is implemented but the specific implementations of how this structure works will depend on how it is programmed. This is an example of an abstract data types as we are not concerned with the underlying method, just the abstract functions that allow us to interact with it.
Stacks are an example of a LIFO or a Last-In, First-Out structure. This means that the last element that was added to a stack will be the first element returned when accessed. Stacks have a set of functions that should be implemented no matter where it is:
| Function | Description |
|---|---|
push(element) |
Pushes an element on to the top of the stack. |
pop() |
Removes an element from the top of the stack and then returns it |
empty() |
Checks if the stack is empty |
full() |
Checks is the stack is at maximum capacity |
Some implementations will have slightly varying names for these functions such as isFull and isEmpty()
Some stacks are defined with a fixed size but this depends on the implementation. The idea of the top and bottom of the stack are rather arbitrary, you just need to ensure to remember that items are added and removed from the same end. An example of stack in use is shown below.
stack = new Stack(4); // Define a stack with a maximum capacity of 4 elements.
stack.empty(); // -> True
stack.push(10);
//Stack: [0] 10
stack.pop(); // -> 10
//Stack: empty
stack.push(23);
stack.push(53);
stack.push(12);
stack.push(1);
//Stack: [0] 1
// [1] 12
// [2] 53
// [3] 23
stack.full() // -> True
stack.pop() // -> 1
//Stack: [0] 12
// [1] 53
// [2] 23
Queue
[edit | edit source]A queue is similar to a Stack in the idea that is is an abstract data store that follows a set of rules. It is a FIFO structure or First-In, First-Out meaning that the first piece of data added will be the first piece of data returned when it is queried (how queues work in real life, usually).
It defines its own set of functions:
| Function | Description |
|---|---|
enqueue(element) |
Pushes an element on to the top of the queue. |
dequeue() |
Removes an element from the bottom of the queue and then returns it |
empty() |
Checks if the queue is empty |
full() |
Checks is the queue is at maximum capacity |
An example of how to use this is shown below but it has many very useful and real uses within real world programming. For example, if a set of tasks need to be executed, a queue can be used to ensure that they are executed in the order that they were added.
queue = new Queue(4); // Define a queue with a maximum of 4 elements.
queue.empty(); // -> True
queue.enqueue(23)
queue.enqueue(53);
queue.enqueue(12);
queue.enqueue(1);
// Queue: [0] 23
// [1] 53
// [2] 12
// [3] 1
queue.full(); // -> True
queue.dequeue(); // -> 23
queue.dequeue(); // -> 53
// Queue: [0] 12
// [1] 1
Traversable Structures
[edit | edit source]Tree
[edit | edit source]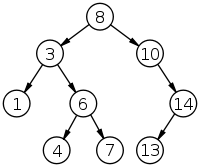
A tree is a type of data structure that is made up of stems and leaves. There are a number of different types of tree but you only need to be aware of the basics and the features of a binary search tree.
Trees are formed from a set of nodes, each of which will contain a value. They then connect downwards to another node which may branch out to another node and so on or will end that chain. An example of a tree is shown to the side
Binary Search Trees
[edit | edit source]A binary search tree is a specific implementation of a tree that follows a set of rules. This kind of tree will have a 'comparison function' or something by a similar name that controls at what position within the tree data will be inserted. This could be something as simple as 'a > b' where a is the data to insert and b is the current node. Any trees that only have 2 branches is acknowledged as binary tree.
Insertion
[edit | edit source]When data is inserted, it follows a path through the tree using the comparison function. In the image shown to the side, if we were adding the data 9 then it would go to the root node 8. As the value is bigger it goes to the right and would go to the 10 node. As the value is smaller it would then go to the left. As there is no node there, it would add the node at that position.
If there was a node to the left, the process would have continued until it reached a point where there was no child node and it would be inserted there. Where duplicates will be placed within a graph depends on how the comparison function is written.
Traversal
[edit | edit source]Trees can be traversed in four different ways which dictates how you travel through the nodes and therefore controls the order in which nodes will be returned.
Preorder Traversal
[edit | edit source]
The official procedure for a preorder traversal is as follows:
- If the node is not null/empty then continue
- Output the data of the current node
- Go to the left and start again
- Go to the right and start again
The two last steps are achieved by calling this function recursively.
When doing this by hand, you can just draw a line to the left of the nodes and drawing a line around the nodes as shown in the image to the right. This method works for each traversal, it just depends where you draw the lines.
Inorder Traversal
[edit | edit source]
The official procedure for a inorder traversal is as follows:
- If the node is not null/empty then continue
- Go to the left and start again
- Output the data of the current node
- Go to the right and start again
The 2nd and 4th steps are achieved by calling this function recursively.
When doing this by hand, you can just draw a line down from each of the nodes and drawing a line around the nodes as shown in the image to the right. This method works for each traversal, it just depends where you draw the lines.
Postorder Traversal
[edit | edit source]
The official procedure for a postorder traversal is as follows:
- If the node is not null/empty then continue
- Go to the left and start again
- Go to the right and start again
- Output the data of the current node
The 2nd and 3rd steps are achieved by calling this function recursively.
When doing this by hand, you can just draw a line to the right of the nodes and drawing a line around the nodes as shown in the image to the right. This method works for each traversal, it just depends where you draw the lines.
Breadth First Traversal
[edit | edit source]
Breadth first traversal does not have a specific procedure on how to access nodes but it is very easy to guess. It visits each level of the tree in order and outputs the content of the nodes from left to right.
You do not need to know how to implement this but it is worth knowing just how it works.
Graph
[edit | edit source]A graph is similar to a tree but has much more complexity. It is made up of nodes and connections like a tree but instead of each node only connecting down, any node can connect to another. Each connection will either have a direction associated with it (for example a connects to b) in which case the graph is called directed, or it will have no direction (for example a and b have a connection) in which case it is called undirected.
Graphs are exceptionally good at modelling large amounts of complex data as it allows for a more natural method of connecting data. Some graphs will be shown with numbers next to their connections, these are called weightings and affect how traversals work when using algorithms such as Dijkstra's.
You must know how to traverse a graph data structure as well which comes in the form of two algorithms. These are copied verbatim from the OCR Computing book.
Depth-First Traversal
[edit | edit source]PUSH the first node onto the stack
Mark as visited
Repeat
Visit the next unvisited node to the one on the top of the stack
Mark as visited
PUSH this node onto the stack
If no node to visit POP node off the stack
Until the stack is empty
Breadth-First Traversal
[edit | edit source]PUSH the first node into the queue
Mark as visited
Repeat
Visit the unvisited nodes connected to the first node
PUSH nodes onto queue
Until all nodes visited
Repeat
POP next node from queue
Repeat
Visit unvisited nodes connected to current node
PUSH nodes into queue
Until all nodes visited
Until queue empty
Hash Tables
[edit | edit source]Data is stored in a memory location generated by passing the data's identifier through a hash function. The hash function generates a memory address to store the data for an item, it always returns the same answer for a particular input identifier.
Some simple hash functions give the same memory address to different items of data. In these cases a method for recalculating the duplicated addresses will be stated. This might go to the next available memory address or check every third memory address afterwards until one is available.