Tree traversal
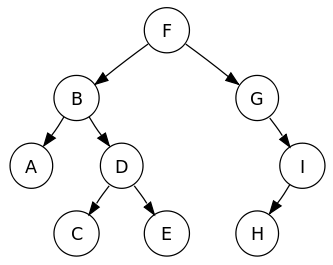
A tree is a special case of a graph, and therefore the graph traversal algorithms of the previous chapter also apply to trees. A graph traversal can start at any node, but in the case of a tree the traversal always starts at the root node. Binary trees can be traversed in three additional ways. The following tree will be used as the recurring example.
Breadth-first
[edit | edit source]Traversing a tree in breadth-first order means that after visiting a node X, all of X's children are visited, then all of X's 'grand-children' (i.e. the children's children), then all of X's 'great-grand-children', etc. In other words, the tree is traversed by sweeping through the breadth of a level before visiting the next level down, as shown in this animation:
The children of a node may be visited in any order, but remember the algorithm uses a queue, so if a node X is enqueued (grey in the animation) before node Y, then X's children will be visited (black in the animation) before Y's children. For the example tree at the start of this chapter, two possible breadth-first traversals are F B G A D I C E H and F G B I D A H E C. In the second traversal, G is visited before B, so I is visited before A and D.
|
Exercise: Breadth First Traversal List two other possible breadth-first traversals of the same tree. Answer: Since F, B and D each have two children, there are in total 2*2*2=8 possible breadth-first traversals:
The first and last traversals were already given above, so you could have listed any other two. |
Depth-first
[edit | edit source]As the name implies, a depth-first traversal will go down one branch of the tree as far as possible, i.e. until it stops at a leaf, before trying any other branch. The various branches starting from the same parent may be explored in any order. For the example tree, two possible depth-first traversals are F B A D C E G I H and F G I H B D E C A.
|
Exercise: Breadth First Traversal List two other possible depth-first traversals of the same tree. Answer: Since F, B and D each have two children, there are in total 2*2*2=8 possible depth-first traversals:
The first and last traversals were already given above, so you could have listed any other two. |
|
Exercise: Depth and Breadth First Traversal
|
- Depth First traversal generally uses a Stack
- Breadth First generally uses a Queue
Pre-order
[edit | edit source]Binary trees are usually traversed from left to right, but right-to-left traversal is also possible and might appear in the exam questions. We will therefore make the direction always clear in the rest of this chapter.
If each node is visited before both of its subtrees, then it's called a pre-order traversal. The algorithm for left-to-right pre-order traversal is:
- Visit the root node (generally output it)
- Do a pre-order traversal of the left subtree
- Do a pre-order traversal of the right subtree
which can be implemented as follows, using the tree data structure defined in the previous unit:
sub PreOrder(TreeNode)
Output(TreeNode.value)
If LeftPointer(TreeNode) != NULL Then
PreOrder(TreeNode.LeftNode)
If RightPointer(TreeNode) != NULL Then
PreOrder(TreeNode.RightNode)
end sub
Since the algorithm completely determines the order in which nodes are visited, there is only one possible left-to-right pre-order traversal for each binary tree. For our example tree, which is a binary tree, it's F B A D C E G I H.
Because a pre-order traversal always goes down one branch (left or right) before moving on to the other branch, a pre-order traversal is always one of the possible depth-first traversals.
Post-order
[edit | edit source]If each node is visited after its subtrees, then it's a post-order traversal. The algorithm for left-to-right post-order traversal is:
- Do a post-order traversal of the left subtree
- Do a post-order traversal of the right subtree
- Visit the root node (generally output this)
which can be implemented as:
sub PostOrder(TreeNode)
If LeftPointer(TreeNode) != NULL Then
PostOrder(TreeNode.LeftNode)
If RightPointer(TreeNode) != NULL Then
PostOrder(TreeNode.RightNode)
Output(TreeNode.value)
end sub
There is only one left-to-right post-order traversal for each binary tree. For our example tree, it's A C E D B H I G F.
In-order
[edit | edit source]If each node is visited between visiting its left and right subtrees, then it's an in-order traversal. The algorithm for left-to-right in-order traversal is:
- Do an in-order traversal of the left subtree
- Visit root node (generally output this)
- Do an in-order traversal of the right subtree
which can be implemented as:
sub InOrder(TreeNode)
If LeftPointer(TreeNode) != NULL Then
InOrder(TreeNode.LeftNode)
Output(TreeNode.value)
If RightPointer(TreeNode) != NULL Then
InOrder(TreeNode.RightNode)
end sub
There is only one left-to-right in-order traversal for each binary tree. For our example tree, it's A B C D E F G H I. Note the nodes are visited in ascending order. That's no coincidence.
In binary search trees like our example tree, the values in the left subtree are smaller than the root and the values in the right subtree are larger than the root, so a left-to-right in-order traversal visits the nodes in ascending order.
|
Exercise: In-order Traversal Is the statement "an in-order traversal always visits the nodes in ascending order" true or false? Answer: It is false. An in-order traversal only visits the nodes in ascending order if it's a left-to-right traversal and the tree is a binary search tree. How would you change the algorithm above to visit the nodes of a binary search tree in descending order ? Answer: A right-to-left in-order traversal would produce the desired order:
|
Traversal Tips
[edit | edit source]In the exam, you may be given some traversal pseudo-code and a binary tree, and asked to list the nodes in the order the code will visit them.
The first thing is to look carefully at the code and check:
- is the node visited before (pre-order), between (in-order) or after (post-order) visiting the subtrees?
- is the left subtree visited before the right subtree or the other way round?
For example, the following code does a left-to-right traversal and the comments show where the visit of the root might take place.
sub Traversal(TreeNode)
'Output(TreeNode.value) REM Pre-Order
If LeftPointer(TreeNode) != NULL Then
Traversal(TreeNode.LeftNode)
'Output(TreeNode.value) REM In-Order
If RightPointer(TreeNode) != NULL Then
Traversal(TreeNode.RightNode)
'Output(TreeNode.value) REM Post-Order
end sub
Let's assume it's left-to-right traversal. Once you know, from the position of the node visit, if it's a pre-, in- or post-order traversal, you can annotate each node of the binary tree as follows:

| Type of Traversal | Position of Output code | Where to put your mark |
|---|---|---|
| Pre | Top | Left |
| In | Middle | Bottom |
| Post | Bottom | Right |
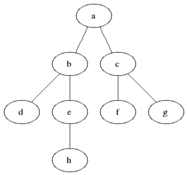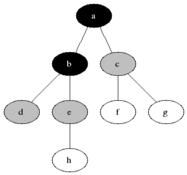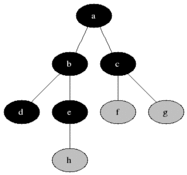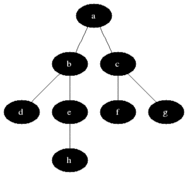
Finally, draw a line going anticlockwise around the tree, connecting the marks. Follow the line and write down each node as you meet a mark: that will be the order in which the code will visit the nodes. Here are the three possible left-to-right traversals:
- The 3 different types of left-to-right traversal
-
Pre-order
FBADCEGIH -
In-order
ABCDEFGHI -
Post-order
ACEDBHIGF
As you can see, following this tip you obtain the same answers as in the sections above.
If the traversal is right to left, you have to draw a clockwise line and swap the position of the pre-order or post-order mark.
| Type of Traversal | Position of Output code | Mark for left-to-right traversal | Mark for right-to-left traversal |
|---|---|---|---|
| Pre | Top | Left | Right |
| In | Middle | Bottom | Bottom |
| Post | Bottom | Right | Left |
If the tree is a binary search tree and you're asked for an in-order traversal, you should have visited the nodes in ascending order (for left-to-right traversal) or descending order (for right-to-left traversal). If it's not a binary search tree, the in-order traversal won't visit the nodes in neither ascending nor descending order, but a pre-order or post-order traversal might, it will all depend where the nodes are placed in the tree.
Although in this chapter we have always made explicit whether it was a left-to-right or right-to-left traversal for clarity, the typical usage of the terms pre-order, in-order and post-order implies a left-to-right traversal, if nothing to the contrary is said.




