User:唐舞麟/sandbox

3 - Projection Onto a Subspace

This subsection, like the others in this section, is optional. It also requires material from the optional earlier subsection on Combining Subspaces.

The prior subsections project a vector onto a line by decomposing it into two parts: the part in the line ${\mbox{proj}}_{[{\vec {s}}\,]}({{\vec {v}}\,})$ and the rest ${\vec {v}}-{\mbox{proj}}_{[{\vec {s}}\,]}({{\vec {v}}\,})$. To generalize projection to arbitrary subspaces, we follow this idea.

Definition 3.1

For any direct sum $V=M\oplus N$ and any ${\vec {v}}\in V$, the projection of ${\vec {v}}$ onto $M$ along $N$ is

${\mbox{proj}}_{M,N}({{\vec {v}}\,})={\vec {m}}$

where ${\vec {v}}={\vec {m}}+{\vec {n}}$ with ${\vec {m}}\in M,\,{\vec {n}}\in N$.

This definition doesn't involve a sense of "orthogonal" so we can apply it to spaces other than subspaces of an $\mathbb {R} ^{n}$. (Definitions of orthogonality for other spaces are perfectly possible, but we haven't seen any in this book.)

Example 3.2

The space ${\mathcal {M}}_{2\!\times \!2}$ of $2\!\times \!2$ matrices is the direct sum of these two.

$M=\{{\begin{pmatrix}a&b\\0&0\end{pmatrix}}\,{\big |}\,a,b\in \mathbb {R} \}\qquad N=\{{\begin{pmatrix}0&0\\c&d\end{pmatrix}}\,{\big |}\,c,d\in \mathbb {R} \}$

To project

$A={\begin{pmatrix}3&1\\0&4\end{pmatrix}}$

onto $M$ along $N$, we first fix bases for the two subspaces.

$B_{M}=\langle {\begin{pmatrix}1&0\\0&0\end{pmatrix}},{\begin{pmatrix}0&1\\0&0\end{pmatrix}}\rangle \qquad B_{N}=\langle {\begin{pmatrix}0&0\\1&0\end{pmatrix}},{\begin{pmatrix}0&0\\0&1\end{pmatrix}}\rangle$

The concatenation of these

$B=B_{M}\!{\mathbin {{}^{\frown }}}\!B_{N}=\langle {\begin{pmatrix}1&0\\0&0\end{pmatrix}},{\begin{pmatrix}0&1\\0&0\end{pmatrix}},{\begin{pmatrix}0&0\\1&0\end{pmatrix}},{\begin{pmatrix}0&0\\0&1\end{pmatrix}}\rangle$

is a basis for the entire space, because the space is the direct sum, so we can use it to represent $A$.

${\begin{pmatrix}3&1\\0&4\end{pmatrix}}=3\cdot {\begin{pmatrix}1&0\\0&0\end{pmatrix}}+1\cdot {\begin{pmatrix}0&1\\0&0\end{pmatrix}}+0\cdot {\begin{pmatrix}0&0\\1&0\end{pmatrix}}+4\cdot {\begin{pmatrix}0&0\\0&1\end{pmatrix}}$

Now the projection of $A$ onto $M$ along $N$ is found by keeping the $M$ part of this sum and dropping the $N$ part.

${\mbox{proj}}_{M,N}({\begin{pmatrix}3&1\\0&4\end{pmatrix}})=3\cdot {\begin{pmatrix}1&0\\0&0\end{pmatrix}}+1\cdot {\begin{pmatrix}0&1\\0&0\end{pmatrix}}={\begin{pmatrix}3&1\\0&0\end{pmatrix}}$

Example 3.3

Both subscripts on ${\mbox{proj}}_{M,N}({{\vec {v}}\,})$ are significant. The first subscript $M$ matters because the result of the projection is an ${\vec {m}}\in M$, and changing this subspace would change the possible results. For an example showing that the second subscript matters, fix this plane subspace of $\mathbb {R} ^{3}$ and its basis

$M=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,y-2z=0\}\qquad B_{M}=\langle {\begin{pmatrix}1\\0\\0\end{pmatrix}},{\begin{pmatrix}0\\2\\1\end{pmatrix}}\rangle$

and compare the projections along two different subspaces.

$N=\{k{\begin{pmatrix}0\\0\\1\end{pmatrix}}\,{\big |}\,k\in \mathbb {R} \}\qquad {\hat {N}}=\{k{\begin{pmatrix}0\\1\\-2\end{pmatrix}}\,{\big |}\,k\in \mathbb {R} \}$

(Verification that $\mathbb {R} ^{3}=M\oplus N$ and $\mathbb {R} ^{3}=M\oplus {\hat {N}}$ is routine.) We will check that these projections are different by checking that they have different effects on this vector.

${\vec {v}}={\begin{pmatrix}2\\2\\5\end{pmatrix}}$

For the first one we find a basis for $N$

$B_{N}=\langle {\begin{pmatrix}0\\0\\1\end{pmatrix}}\rangle$

and represent ${\vec {v}}$ with respect to the concatenation $B_{M}\!{\mathbin {{}^{\frown }}}\!B_{N}$.

${\begin{pmatrix}2\\2\\5\end{pmatrix}}=2\cdot {\begin{pmatrix}1\\0\\0\end{pmatrix}}+1\cdot {\begin{pmatrix}0\\2\\1\end{pmatrix}}+4\cdot {\begin{pmatrix}0\\0\\1\end{pmatrix}}$

The projection of ${\vec {v}}$ onto $M$ along $N$ is found by keeping the $M$ part and dropping the $N$ part.

${\mbox{proj}}_{M,N}({{\vec {v}}\,})=2\cdot {\begin{pmatrix}1\\0\\0\end{pmatrix}}+1\cdot {\begin{pmatrix}0\\2\\1\end{pmatrix}}={\begin{pmatrix}2\\2\\1\end{pmatrix}}$

For the other subspace ${\hat {N}}$, this basis is natural.

$B_{\hat {N}}=\langle {\begin{pmatrix}0\\1\\-2\end{pmatrix}}\rangle$

Representing ${\vec {v}}$ with respect to the concatenation

${\begin{pmatrix}2\\2\\5\end{pmatrix}}=2\cdot {\begin{pmatrix}1\\0\\0\end{pmatrix}}+(9/5)\cdot {\begin{pmatrix}0\\2\\1\end{pmatrix}}-(8/5)\cdot {\begin{pmatrix}0\\1\\-2\end{pmatrix}}$

and then keeping only the $M$ part gives this.

${\mbox{proj}}_{M,{\hat {N}}}({{\vec {v}}\,})=2\cdot {\begin{pmatrix}1\\0\\0\end{pmatrix}}+(9/5)\cdot {\begin{pmatrix}0\\2\\1\end{pmatrix}}={\begin{pmatrix}2\\18/5\\9/5\end{pmatrix}}$

Therefore projection along different subspaces may yield different results.

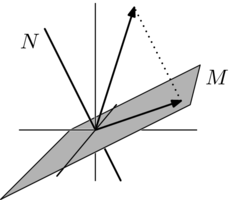
These pictures compare the two maps. Both show that the projection is indeed "onto" the plane and "along" the line.

Notice that the projection along $N$ is not orthogonal— there are members of the plane $M$ that are not orthogonal to the dotted line. But the projection along ${\hat {N}}$ is orthogonal.

A natural question is: what is the relationship between the projection operation defined above, and the operation of orthogonal projection onto a line? The second picture above suggests the answer— orthogonal projection onto a line is a special case of the projection defined above; it is just projection along a subspace perpendicular to the line.

In addition to pointing out that projection along a subspace is a generalization, this scheme shows how to define orthogonal projection onto any subspace of $\mathbb {R} ^{n}$, of any dimension.

Definition 3.4

The orthogonal complementof a subspace $M$ of $\mathbb {R} ^{n}$ is

$M^{\perp }=\{{\vec {v}}\in \mathbb {R} ^{n}\,{\big |}\,{\vec {v}}{\text{ is perpendicular to all vectors in }}M\}$

(read "$M$ perp"). The orthogonal projection ${\mbox{proj}}_{M}({{\vec {v}}\,})$ of a vector is its projection onto $M$ along $M^{\perp }$.

Example 3.5

In $\mathbb {R} ^{3}$, to find the orthogonal complement of the plane

$P=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,3x+2y-z=0\}$

we start with a basis for $P$.

$B=\langle {\begin{pmatrix}1\\0\\3\end{pmatrix}},{\begin{pmatrix}0\\1\\2\end{pmatrix}}\rangle$

Any ${\vec {v}}$ perpendicular to every vector in $B$ is perpendicular to every vector in the span of $B$ (the proof of this assertion is Problem 10). Therefore, the subspace $P^{\perp }$ consists of the vectors that satisfy these two conditions.

${\begin{pmatrix}1\\0\\3\end{pmatrix}}\cdot {\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}=0\qquad {\begin{pmatrix}0\\1\\2\end{pmatrix}}\cdot {\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}=0$

We can express those conditions more compactly as a linear system.

$P^{\perp }=\{{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}\,{\big |}\,{\begin{pmatrix}1&0&3\\0&1&2\end{pmatrix}}{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}\}$

We are thus left with finding the nullspace of the map represented by the matrix, that is, with calculating the solution set of a homogeneous linear system.

$P^{\perp }=\{{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}\,{\big |}\,\;{\begin{array}{*{3}{rc}r}v_{1}&&&+&3v_{3}&=&0\\&&v_{2}&+&2v_{3}&=&0\end{array}}\;\}=\{k{\begin{pmatrix}-3\\-2\\1\end{pmatrix}}\,{\big |}\,k\in \mathbb {R} \}$

Example 3.6

Where $M$ is the $xy$-plane subspace of $\mathbb {R} ^{3}$, what is $M^{\perp }$? A common first reaction is that $M^{\perp }$ is the $yz$-plane, but that's not right. Some vectors from the $yz$-plane are not perpendicular to every vector in the $xy$-plane.

${\begin{pmatrix}1\\1\\0\end{pmatrix}}\not \perp {\begin{pmatrix}0\\3\\2\end{pmatrix}}$

$\displaystyle \theta =\arccos({\frac {1\cdot 0+1\cdot 3+0\cdot 2}{{\sqrt {2}}\cdot {\sqrt {13}}}})\approx {\text{0.94 rad}}$

Instead $M^{\perp }$ is the $z$-axis, since proceeding as in the prior example and taking the natural basis for the $xy$-plane gives this.

$M^{\perp }=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,{\begin{pmatrix}1&0&0\\0&1&0\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}\;\}=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,x=0{\text{ and }}y=0\}$

The two examples that we've seen since Definition 3.4 illustrate the first sentence in that definition. The next result justifies the second sentence.

Lemma 3.7

Let $M$ be a subspace of $\mathbb {R} ^{n}$. The orthogonal complement of $M$ is also a subspace. The space is the direct sum of the two $\mathbb {R} ^{n}=M\oplus M^{\perp }$. And, for any ${\vec {v}}\in \mathbb {R} ^{n}$, the vector ${\vec {v}}-{\mbox{proj}}_{M}({{\vec {v}}\,})$ is perpendicular to every vector in $M$.

Proof

First, the orthogonal complement $M^{\perp }$ is a subspace of $\mathbb {R} ^{n}$ because, as noted in the prior two examples, it is a nullspace.

Next, we can start with any basis $B_{M}=\langle {\vec {\mu }}_{1},\dots ,{\vec {\mu }}_{k}\rangle$ for $M$ and expand it to a basis

for the entire space. Apply the Gram-Schmidt process to get an orthogonal basis $K=\langle {\vec {\kappa }}_{1},\dots ,{\vec {\kappa }}_{n}\rangle$ for $\mathbb {R} ^{n}$. This $K$ is the concatenation of two bases $\langle {\vec {\kappa }}_{1},\dots ,{\vec {\kappa }}_{k}\rangle$ (with the same number of members as $B_{M}$) and $\langle {\vec {\kappa }}_{k+1},\dots ,{\vec {\kappa }}_{n}\rangle$. The first is a basis for $M$, so if we show that the second is a basis for $M^{\perp }$ then we will have that the entire space is the direct sum of the two subspaces.

Problem 9 from the prior subsection proves this about any orthogonal basis: each vector ${\vec {v}}$ in the space is the sum of its orthogonal projections onto the lines spanned by the basis vectors.

${\vec {v}}={\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{n}]}({{\vec {v}}\,})\qquad \qquad (*)$

To check this, represent the vector ${\vec {v}}=r_{1}{\vec {\kappa }}_{1}+\dots +r_{n}{\vec {\kappa }}_{n}$, apply ${\vec {\kappa }}_{i}$ to both sides ${\vec {v}}\cdot {\vec {\kappa }}_{i}=\left(r_{1}{\vec {\kappa }}_{1}+\dots +r_{n}{\vec {\kappa }}_{n}\right)\cdot {\vec {\kappa }}_{i}=r_{1}\cdot 0+\dots +r_{i}\cdot ({\vec {\kappa }}_{i}\cdot {\vec {\kappa }}_{i})+\dots +r_{n}\cdot 0$, and solve to get $r_{i}=({\vec {v}}\cdot {\vec {\kappa }}_{i})/({\vec {\kappa }}_{i}\cdot {\vec {\kappa }}_{i})$, as desired.

Since obviously any member of the span of $\langle {\vec {\kappa }}_{k+1},\dots ,{\vec {\kappa }}_{n}\rangle$ is orthogonal to any vector in $M$, to show that this is a basis for $M^{\perp }$ we need only show the other containment— that any ${\vec {w}}\in M^{\perp }$ is in the span of this basis. The prior paragraph does this. On projections onto basis vectors from $M$, any ${\vec {w}}\in M^{\perp }$ gives ${\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {w}}\,})={\vec {0}},\dots ,\,{\mbox{proj}}_{[{\vec {\kappa }}_{k}]}({{\vec {w}}\,})={\vec {0}}$ and therefore ($*$) gives that ${\vec {w}}$ is a linear combination of ${\vec {\kappa }}_{k+1},\dots ,{\vec {\kappa }}_{n}$. Thus this is a basis for $M^{\perp }$ and $\mathbb {R} ^{n}$ is the direct sum of the two.

The final sentence is proved in much the same way. Write ${\vec {v}}={\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{n}]}({{\vec {v}}\,})$. Then ${\mbox{proj}}_{M}({{\vec {v}}\,})$ is gotten by keeping only the $M$ part and dropping the $M^{\perp }$ part ${\mbox{proj}}_{M}({{\vec {v}}\,})={\mbox{proj}}_{[{\vec {\kappa }}_{k+1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{k}]}({{\vec {v}}\,})$. Therefore ${\vec {v}}-{\mbox{proj}}_{M}({{\vec {v}}\,})$ consists of a linear combination of elements of $M^{\perp }$ and so is perpendicular to every vector in $M$.

We can find the orthogonal projection onto a subspace by following the steps of the proof, but the next result gives a convienent formula.

Theorem 3.8

Let ${\vec {v}}$ be a vector in $\mathbb {R} ^{n}$ and let $M$ be a subspace of $\mathbb {R} ^{n}$ with basis $\langle {\vec {\beta }}_{1},\dots ,{\vec {\beta }}_{k}\rangle$. If $A$ is the matrix whose columns are the ${\vec {\beta }}$'s then ${\mbox{proj}}_{M}({{\vec {v}}\,})=c_{1}{\vec {\beta }}_{1}+\dots +c_{k}{\vec {\beta }}_{k}$ where the coefficients $c_{i}$ are the entries of the vector $({{A}^{\rm {trans}}}A)^{-1}{{A}^{\rm {trans}}}\cdot {\vec {v}}$. That is, ${\mbox{proj}}_{M}({{\vec {v}}\,})=A({{A}^{\rm {trans}}}A)^{-1}{{A}^{\rm {trans}}}\cdot {\vec {v}}$.

Proof

The vector ${\mbox{proj}}_{M}({\vec {v}})$ is a member of $M$ and so it is a linear combination of basis vectors $c_{1}\cdot {\vec {\beta }}_{1}+\dots +c_{k}\cdot {\vec {\beta }}_{k}$. Since $A$'s columns are the ${\vec {\beta }}$'s, that can be expressed as: there is a ${\vec {c}}\in \mathbb {R} ^{k}$ such that ${\mbox{proj}}_{M}({{\vec {v}}\,})=A{\vec {c}}$ (this is expressed compactly with matrix multiplication as in Example 3.5 and 3.6). Because ${\vec {v}}-{\mbox{proj}}_{M}({{\vec {v}}\,})$ is perpendicular to each member of the basis, we have this (again, expressed compactly).

${\vec {0}}={{A}^{\rm {trans}}}{\bigl (}{\vec {v}}-A{\vec {c}}{\bigr )}={{A}^{\rm {trans}}}{\vec {v}}-{{A}^{\rm {trans}}}A{\vec {c}}$

Solving for ${\vec {c}}$ (showing that ${{A}^{\rm {trans}}}A$ is invertible is an exercise)

${\vec {c}}={\bigl (}{{A}^{\rm {trans}}}A{\bigr )}^{-1}{{A}^{\rm {trans}}}\cdot {\vec {v}}$

gives the formula for the projection matrix as ${\mbox{proj}}_{M}({{\vec {v}}\,})=A\cdot {\vec {c}}$.

Example 3.9

To orthogonally project this vector onto this subspace

${\vec {v}}={\begin{pmatrix}1\\-1\\1\end{pmatrix}}\qquad P=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,x+z=0\}$

first make a matrix whose columns are a basis for the subspace

$A={\begin{pmatrix}0&1\\1&0\\0&-1\end{pmatrix}}$

and then compute.

${\begin{array}{rl}A{\bigl (}{{A}^{\rm {trans}}}A{\bigr )}^{-1}{{A}^{\rm {trans}}}&={\begin{pmatrix}0&1\\1&0\\0&-1\end{pmatrix}}{\begin{pmatrix}0&1\\1/2&0\end{pmatrix}}{\begin{pmatrix}1&0&-1\\0&1&0\end{pmatrix}}\\&={\begin{pmatrix}1/2&0&-1/2\\0&1&0\\-1/2&0&1/2\end{pmatrix}}\end{array}}$

With the matrix, calculating the orthogonal projection of any vector onto $P$ is easy.

${\mbox{proj}}_{P}({\vec {v}})={\begin{pmatrix}1/2&0&-1/2\\0&1&0\\-1/2&0&1/2\end{pmatrix}}{\begin{pmatrix}1\\-1\\1\end{pmatrix}}={\begin{pmatrix}0\\-1\\0\end{pmatrix}}$

Exercises

This exercise is recommended for all readers.

Problem 1

Project the vectors onto $M$ along $N$.

1. ${\begin{pmatrix}3\\-2\end{pmatrix}},\quad M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x+y=0\},\quad N=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,-x-2y=0\}$
2. ${\begin{pmatrix}1\\2\end{pmatrix}},\quad M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x-y=0\},\quad N=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,2x+y=0\}$
3. ${\begin{pmatrix}3\\0\\1\end{pmatrix}},\quad M=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,x+y=0\},\quad N=\{c\cdot {\begin{pmatrix}1\\0\\1\end{pmatrix}}\,{\big |}\,c\in \mathbb {R} \}$

This exercise is recommended for all readers.

Problem 2

Find $M^{\perp }$.

1. $M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x+y=0\}$
2. $M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,-2x+3y=0\}$
3. $M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x-y=0\}$
4. $M=\{{\vec {0}}\,\}$
5. $M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x=0\}$
6. $M=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,-x+3y+z=0\}$
7. $M=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,x=0{\text{ and }}y+z=0\}$

Problem 3

This subsection shows how to project orthogonally in two ways, the method of Example 3.2 and 3.3, and the method of Theorem 3.8. To compare them, consider the plane $P$ specified by $3x+2y-z=0$ in $\mathbb {R} ^{3}$.

1. Find a basis for $P$.
2. Find $P^{\perp }$ and a basis for $P^{\perp }$.
3. Represent this vector with respect to the concatenation of the two bases from the prior item.

   ${\vec {v}}={\begin{pmatrix}1\\1\\2\end{pmatrix}}$

4. Find the orthogonal projection of ${\vec {v}}$ onto $P$ by keeping only the $P$ part from the prior item.
5. Check that against the result from applying Theorem 3.8.

This exercise is recommended for all readers.

Problem 4

We have three ways to find the orthogonal projection of a vector onto a line, the Definition 1.1 way from the first subsection of this section, the Example 3.2 and 3.3 way of representing the vector with respect to a basis for the space and then keeping the $M$ part, and the way of Theorem 3.8. For these cases, do all three ways.

1. ${\vec {v}}={\begin{pmatrix}1\\-3\end{pmatrix}},\quad M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x+y=0\}$
2. ${\vec {v}}={\begin{pmatrix}0\\1\\2\end{pmatrix}},\quad M=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,x+z=0{\text{ and }}y=0\}$

Problem 5

Check that the operation of Definition 3.1 is well-defined. That is, in Example 3.2 and 3.3, doesn't the answer depend on the choice of bases?

Problem 6

What is the orthogonal projection onto the trivial subspace?

Problem 7

What is the projection of ${\vec {v}}$ onto $M$ along $N$ if ${\vec {v}}\in M$?

Problem 8

Show that if $M\subseteq \mathbb {R} ^{n}$ is a subspace with orthonormal basis $\langle {\vec {\kappa }}_{1},\ldots ,{\vec {\kappa }}_{n}\rangle$ then the orthogonal projection of ${\vec {v}}$ onto $M$ is this.

$({\vec {v}}\cdot {\vec {\kappa }}_{1})\cdot {\vec {\kappa }}_{1}+\dots +({\vec {v}}\cdot {\vec {\kappa }}_{n})\cdot {\vec {\kappa }}_{n}$

This exercise is recommended for all readers.

Problem 9

Prove that the map $p:V\to V$ is the projection onto $M$ along $N$ if and only if the map ${\mbox{id}}-p$ is the projection onto $N$ along $M$. (Recall the definition of the difference of two maps: $({\mbox{id}}-p)\,({\vec {v}})={\mbox{id}}({\vec {v}})-p({\vec {v}})={\vec {v}}-p({\vec {v}})$.)

This exercise is recommended for all readers.

Problem 10

Show that if a vector is perpendicular to every vector in a set then it is perpendicular to every vector in the span of that set.

Problem 11

True or false: the intersection of a subspace and its orthogonal complement is trivial.

Problem 12

Show that the dimensions of orthogonal complements add to the dimension of the entire space.

This exercise is recommended for all readers.

Problem 13

Suppose that ${\vec {v}}_{1},{\vec {v}}_{2}\in \mathbb {R} ^{n}$ are such that for all complements $M,N\subseteq \mathbb {R} ^{n}$, the projections of ${\vec {v}}_{1}$ and ${\vec {v}}_{2}$ onto $M$ along $N$ are equal. Must ${\vec {v}}_{1}$ equal ${\vec {v}}_{2}$? (If so, what if we relax the condition to: all orthogonal projections of the two are equal?)

This exercise is recommended for all readers.

Problem 14

Let $M,N$ be subspaces of $\mathbb {R} ^{n}$. The perp operator acts on subspaces; we can ask how it interacts with other such operations.

1. Show that two perps cancel: $(M^{\perp })^{\perp }=M$.
2. Prove that $M\subseteq N$ implies that $N^{\perp }\subseteq M^{\perp }$.
3. Show that $(M+N)^{\perp }=M^{\perp }\cap N^{\perp }$.

This exercise is recommended for all readers.

Problem 15

The material in this subsection allows us to express a geometric relationship that we have not yet seen between the rangespace and the nullspace of a linear map.

1. Represent $f:\mathbb {R} ^{3}\to \mathbb {R}$ given by

   ${\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}\mapsto 1v_{1}+2v_{2}+3v_{3}$

   with respect to the standard bases and show that

   ${\begin{pmatrix}1\\2\\3\end{pmatrix}}$

   is a member of the perp of the nullspace. Prove that ${\mathcal {N}}(f)^{\perp }$ is equal to the span of this vector.
2. Generalize that to apply to any $f:\mathbb {R} ^{n}\to \mathbb {R}$.
3. Represent $f:\mathbb {R} ^{3}\to \mathbb {R} ^{2}$

   ${\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}\mapsto {\begin{pmatrix}1v_{1}+2v_{2}+3v_{3}\\4v_{1}+5v_{2}+6v_{3}\end{pmatrix}}$

   with respect to the standard bases and show that

   ${\begin{pmatrix}1\\2\\3\end{pmatrix}},\;{\begin{pmatrix}4\\5\\6\end{pmatrix}}$

   are both members of the perp of the nullspace. Prove that ${\mathcal {N}}(f)^{\perp }$ is the span of these two. (Hint. See the third item of Problem 14.)
4. Generalize that to apply to any $f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}$.

This, and related results, is called the Fundamental Theorem of Linear Algebra in (Strang 1993).

Problem 16

Define a projection to be a linear transformation $t:V\to V$ with the property that repeating the projection does nothing more than does the projection alone: $(t\circ t)\,({\vec {v}})=t({\vec {v}})$ for all ${\vec {v}}\in V$.

1. Show that orthogonal projection onto a line has that property.
2. Show that projection along a subspace has that property.
3. Show that for any such $t$ there is a basis $B=\langle {\vec {\beta }}_{1},\ldots ,{\vec {\beta }}_{n}\rangle$ for $V$ such that

   $t({\vec {\beta }}_{i})={\begin{cases}{\vec {\beta }}_{i}&i=1,2,\dots ,\,r\\{\vec {0}}&i=r+1,r+2,\dots ,\,n\end{cases}}$

   where $r$ is the rank of $t$.
4. Conclude that every projection is a projection along a subspace.
5. Also conclude that every projection has a representation

   ${\rm {Rep}}_{B,B}(t)=\left({\begin{array}{c|c}I&Z\\\hline Z&Z\end{array}}\right)$

   in block partial-identity form.

Problem 17

A square matrix is symmetric if each $i,j$ entry equals the $j,i$ entry (i.e., if the matrix equals its transpose). Show that the projection matrix $A({{A}^{\rm {trans}}}A)^{-1}{{A}^{\rm {trans}}}$ is symmetric. (Strang 1980) Hint. Find properties of transposes by looking in the index under "transpose".

Topic: Line of Best Fit

Scientists are often presented with a system that has no solution and they must find an answer anyway. That is, they must find a value that is as close as possible to being an answer.

For instance, suppose that we have a coin to use in flipping. This coin has some proportion $m$ of heads to total flips, determined by how it is physically constructed, and we want to know if $m$ is near $1/2$. We can get experimental data by flipping it many times. This is the result a penny experiment, including some intermediate numbers.

number of flips	30	60	90
number of heads	16	34	51

Because of randomness, we do not find the exact proportion with this sample — there is no solution to this system.

${\begin{array}{*{1}{rc}r}30m&=&16\\60m&=&34\\90m&=&51\end{array}}$

That is, the vector of experimental data is not in the subspace of solutions.

${\begin{pmatrix}16\\34\\51\end{pmatrix}}\not \in \{m{\begin{pmatrix}30\\60\\90\end{pmatrix}}\,{\big |}\,m\in \mathbb {R} \}$

However, as described above, we want to find the $m$ that most nearly works. An orthogonal projection of the data vector into the line subspace gives our best guess.

${\frac {{\begin{pmatrix}16\\34\\51\end{pmatrix}}\cdot {\begin{pmatrix}30\\60\\90\end{pmatrix}}}{{\begin{pmatrix}30\\60\\90\end{pmatrix}}\cdot {\begin{pmatrix}30\\60\\90\end{pmatrix}}}}\cdot {\begin{pmatrix}30\\60\\90\end{pmatrix}}={\frac {7110}{12600}}\cdot {\begin{pmatrix}30\\60\\90\end{pmatrix}}$

The estimate ($m=7110/12600\approx 0.56$) is a bit high but not much, so probably the penny is fair enough.

The line with the slope $m\approx 0.56$ is called the line of best fit for this data.

Minimizing the distance between the given vector and the vector used as the right-hand side minimizes the total of these vertical lengths, and consequently we say that the line has been obtained through fitting by least-squares

(the vertical scale here has been exaggerated ten times to make the lengths visible).

We arranged the equation above so that the line must pass through $(0,0)$ because we take take it to be (our best guess at) the line whose slope is this coin's true proportion of heads to flips. We can also handle cases where the line need not pass through the origin.

For example, the different denominations of U.S. money have different average times in circulation (the $2 bill is left off as a special case). How long should we expect a $25 bill to last?

denomination	1	5	10	20	50	100
average life (years)	1.5	2	3	5	9	20

The plot (see below) looks roughly linear. It isn't a perfect line, i.e., the linear system with equations $b+1m=1.5$, ..., $b+100m=20$ has no solution, but we can again use orthogonal projection to find a best approximation. Consider the matrix of coefficients of that linear system and also its vector of constants, the experimentally-determined values.

$A={\begin{pmatrix}1&1\\1&5\\1&10\\1&20\\1&50\\1&100\end{pmatrix}}\qquad {\vec {v}}={\begin{pmatrix}1.5\\2\\3\\5\\9\\20\end{pmatrix}}$

The ending result in the subsection on Projection into a Subspace says that coefficients $b$ and $m$ so that the linear combination of the columns of $A$ is as close as possible to the vector ${\vec {v}}$ are the entries of $({{A}^{\rm {trans}}}A)^{-1}{{A}^{\rm {trans}}}\cdot {\vec {v}}$. Some calculation gives an intercept of $b=1.05$ and a slope of $m=0.18$.

Plugging $x=25$ into the equation of the line shows that such a bill should last between five and six years.

We close by considering the times for the men's mile race (Oakley & Baker 1977). These are the world records that were in force on January first of the given years. We want to project when a 3:40 mile will be run.

year	1870	1880	1890	1900	1910	1920	1930
seconds	268.8	264.5	258.4	255.6	255.6	252.6	250.4
year	1940	1950	1960	1970	1980	1990	2000
seconds	246.4	241.4	234.5	231.1	229.0	226.3	223.1

We can see below that the data is surprisingly linear. With this input

$A={\begin{pmatrix}1&1860\\1&1870\\\vdots &\vdots \\1&1990\\1&2000\end{pmatrix}}\qquad {\vec {v}}={\begin{pmatrix}280.0\\268.8\\\vdots \\226.3\\223.1\end{pmatrix}}$

the Python program at this Topic's end gives

${\text{slope}}=-0.35$ and ${\text{intercept}}=925.53$ (rounded to two places; the original data is good to only about a quarter of a second since much of it was hand-timed).

When will a $220$ second mile be run? Solving the equation of the line of best fit gives an estimate of the year $2008$.

This example is amusing, but serves as a caution — obviously the linearity of the data will break down someday (as indeed it does prior to 1860).

Exercises

The calculations here are best done on a computer. In addition, some of the problems require more data, available in your library, on the net, in the answers to the exercises, or in the section following the exercises.

Problem 1

Use least-squares to judge if the coin in this experiment is fair.

flips	8	16	24	32	40
heads	4	9	13	17	20

Problem 2

For the men's mile record, rather than give each of the many records and its exact date, we've "smoothed" the data somewhat by taking a periodic sample. Do the longer calculation and compare the conclusions.

Problem 3

Find the line of best fit for the men's $1500$ meter run. How does the slope compare with that for the men's mile? (The distances are close; a mile is about $1609$ meters.)

Problem 4

Find the line of best fit for the records for women's mile.

Problem 5

Do the lines of best fit for the men's and women's miles cross?

Problem 6

When the space shuttle Challenger exploded in 1986, one of the criticisms made of NASA's decision to launch was in the way the analysis of number of O-ring failures versus temperature was made (of course, O-ring failure caused the explosion). Four O-ring failures will cause the rocket to explode. NASA had data from 24 previous flights.

temp °F	53	75	57	58	63	70	70	66	67	67	67
failures	3	2	1	1	1	1	1	0	0	0	0
temp °F	68	69	70	70	72	73	75	76	76	78	79	80	81
failures	0	0	0	0	0	0	0	0	0	0	0	0	0

The temperature that day was forecast to be $31^{\circ }{\text{F}}$.

1. NASA based the decision to launch partially on a chart showing only the flights that had at least one O-ring failure. Find the line that best fits these seven flights. On the basis of this data, predict the number of O-ring failures when the temperature is $31$, and when the number of failures will exceed four.
2. Find the line that best fits all 24 flights. On the basis of this extra data, predict the number of O-ring failures when the temperature is $31$, and when the number of failures will exceed four.

Which do you think is the more accurate method of predicting? (An excellent discussion appears in (Dalal, Folkes & Hoadley 1989).)

Problem 7

This table lists the average distance from the sun to each of the first seven planets, using earth's average as a unit.

Mercury	Venus	Earth	Mars	Jupiter	Saturn	Uranus
0.39	0.72	1.00	1.52	5.20	9.54	19.2

1. Plot the number of the planet (Mercury is $1$, etc.) versus the distance. Note that it does not look like a line, and so finding the line of best fit is not fruitful.
2. It does, however look like an exponential curve. Therefore, plot the number of the planet versus the logarithm of the distance. Does this look like a line?
3. The asteroid belt between Mars and Jupiter is thought to be what is left of a planet that broke apart. Renumber so that Jupiter is $6$, Saturn is $7$, and Uranus is $8$, and plot against the log again. Does this look better?
4. Use least squares on that data to predict the location of Neptune.
5. Repeat to predict where Pluto is.
6. Is the formula accurate for Neptune and Pluto?

This method was used to help discover Neptune (although the second item is misleading about the history; actually, the discovery of Neptune in position $9$ prompted people to look for the "missing planet" in position $5$). See (Gardner 1970)

Problem 8

William Bennett has proposed an Index of Leading Cultural Indicators for the US (Bennett 1993). Among the statistics cited are the average daily hours spent watching TV, and the average combined SAT scores.

	1960	1965	1970	1975	1980	1985	1990	1992
TV	5:06	5:29	5:56	6:07	6:36	7:07	6:55	7:04
SAT	975	969	948	910	890	906	900	899

Suppose that a cause and effect relationship is proposed between the time spent watching TV and the decline in SAT scores (in this article, Mr. Bennett does not argue that there is a direct connection).

1. Find the line of best fit relating the independent variable of average daily TV hours to the dependent variable of SAT scores.
2. Find the most recent estimate of the average daily TV hours (Bennett's cites Neilsen Media Research as the source of these estimates). Estimate the associated SAT score. How close is your estimate to the actual average? (Warning: a change has been made recently in the SAT, so you should investigate whether some adjustment needs to be made to the reported average to make a valid comparison.)

Computer Code

#!/usr/bin/python
# least_squares.py   calculate the line of best fit for a data set
# data file format: each line is two numbers, x and y
n = 0
sum_x = 0
sum_y = 0
sum_x_squared = 0
sum_xy = 0

fn = raw_input("Name of the data file? ")
datafile = open(fn,"r")
while 1:
  ln = datafile.readline()
  if ln:
    data = ln.split()
    x = float(data[0])
    y = float(data[1])
    n += 1
    sum_x += x
    sum_y += y
    sum_x_squared += x*x
    sum_xy += x*y
  else:
    break
datafile.close()

slope = (n*sum_xy - sum_x*sum_y) / (n*sum_x_squared - sum_x**2)
intercept = (sum_y - slope*sum_x)/n
print "line of best fit: slope= %f  intercept= %f" % (slope, intercept)

Additional Data

Data on the progression of the world's records (taken from the Runner's World web site) is below.

Progression of Men's Mile Record
time	name	date
4:52.0	Cadet Marshall (GBR)	02Sep52
4:45.0	Thomas Finch (GBR)	03Nov58
4:40.0	Gerald Surman (GBR)	24Nov59
4:33.0	George Farran (IRL)	23May62
4:29 3/5	Walter Chinnery (GBR)	10Mar68
4:28 4/5	William Gibbs (GBR)	03Apr68
4:28 3/5	Charles Gunton (GBR)	31Mar73
4:26.0	Walter Slade (GBR)	30May74
4:24 1/2	Walter Slade (GBR)	19Jun75
4:23 1/5	Walter George (GBR)	16Aug80
4:19 2/5	Walter George (GBR)	03Jun82
4:18 2/5	Walter George (GBR)	21Jun84
4:17 4/5	Thomas Conneff (USA)	26Aug93
4:17.0	Fred Bacon (GBR)	06Jul95
4:15 3/5	Thomas Conneff (USA)	28Aug95
4:15 2/5	John Paul Jones (USA)	27May11
4:14.4	John Paul Jones (USA)	31May13
4:12.6	Norman Taber (USA)	16Jul15
4:10.4	Paavo Nurmi (FIN)	23Aug23
4:09 1/5	Jules Ladoumegue (FRA)	04Oct31
4:07.6	Jack Lovelock (NZL)	15Jul33
4:06.8	Glenn Cunningham (USA)	16Jun34
4:06.4	Sydney Wooderson (GBR)	28Aug37
4:06.2	Gunder Hagg (SWE)	01Jul42
4:04.6	Gunder Hagg (SWE)	04Sep42
4:02.6	Arne Andersson (SWE)	01Jul43
4:01.6	Arne Andersson (SWE)	18Jul44
4:01.4	Gunder Hagg (SWE)	17Jul45
3:59.4	Roger Bannister (GBR)	06May54
3:58.0	John Landy (AUS)	21Jun54
3:57.2	Derek Ibbotson (GBR)	19Jul57
3:54.5	Herb Elliott (AUS)	06Aug58
3:54.4	Peter Snell (NZL)	27Jan62
3:54.1	Peter Snell (NZL)	17Nov64
3:53.6	Michel Jazy (FRA)	09Jun65
3:51.3	Jim Ryun (USA)	17Jul66
3:51.1	Jim Ryun (USA)	23Jun67
3:51.0	Filbert Bayi (TAN)	17May75
3:49.4	John Walker (NZL)	12Aug75
3:49.0	Sebastian Coe (GBR)	17Jul79
3:48.8	Steve Ovett (GBR)	01Jul80
3:48.53	Sebastian Coe (GBR)	19Aug81
3:48.40	Steve Ovett (GBR)	26Aug81
3:47.33	Sebastian Coe (GBR)	28Aug81
3:46.32	Steve Cram (GBR)	27Jul85
3:44.39	Noureddine Morceli (ALG)	05Sep93
3:43.13	Hicham el Guerrouj (MOR)	07Jul99

Progression of Men's 1500 Meter Record
time	name	date
4:09.0	John Bray (USA)	30May00
4:06.2	Charles Bennett (GBR)	15Jul00
4:05.4	James Lightbody (USA)	03Sep04
3:59.8	Harold Wilson (GBR)	30May08
3:59.2	Abel Kiviat (USA)	26May12
3:56.8	Abel Kiviat (USA)	02Jun12
3:55.8	Abel Kiviat (USA)	08Jun12
3:55.0	Norman Taber (USA)	16Jul15
3:54.7	John Zander (SWE)	05Aug17
3:53.0	Paavo Nurmi (FIN)	23Aug23
3:52.6	Paavo Nurmi (FIN)	19Jun24
3:51.0	Otto Peltzer (GER)	11Sep26
3:49.2	Jules Ladoumegue (FRA)	05Oct30
3:49.0	Luigi Beccali (ITA)	17Sep33
3:48.8	William Bonthron (USA)	30Jun34
3:47.8	Jack Lovelock (NZL)	06Aug36
3:47.6	Gunder Hagg (SWE)	10Aug41
3:45.8	Gunder Hagg (SWE)	17Jul42
3:45.0	Arne Andersson (SWE)	17Aug43
3:43.0	Gunder Hagg (SWE)	07Jul44
3:42.8	Wes Santee (USA)	04Jun54
3:41.8	John Landy (AUS)	21Jun54
3:40.8	Sandor Iharos (HUN)	28Jul55
3:40.6	Istvan Rozsavolgyi (HUN)	03Aug56
3:40.2	Olavi Salsola (FIN)	11Jul57
3:38.1	Stanislav Jungwirth (CZE)	12Jul57
3:36.0	Herb Elliott (AUS)	28Aug58
3:35.6	Herb Elliott (AUS)	06Sep60
3:33.1	Jim Ryun (USA)	08Jul67
3:32.2	Filbert Bayi (TAN)	02Feb74
3:32.1	Sebastian Coe (GBR)	15Aug79
3:31.36	Steve Ovett (GBR)	27Aug80
3:31.24	Sydney Maree (usa)	28Aug83
3:30.77	Steve Ovett (GBR)	04Sep83
3:29.67	Steve Cram (GBR)	16Jul85
3:29.46	Said Aouita (MOR)	23Aug85
3:28.86	Noureddine Morceli (ALG)	06Sep92
3:27.37	Noureddine Morceli (ALG)	12Jul95
3:26.00	Hicham el Guerrouj (MOR)	14Jul98

Progression of Women's Mile Record
time	name	date
6:13.2	Elizabeth Atkinson (GBR)	24Jun21
5:27.5	Ruth Christmas (GBR)	20Aug32
5:24.0	Gladys Lunn (GBR)	01Jun36
5:23.0	Gladys Lunn (GBR)	18Jul36
5:20.8	Gladys Lunn (GBR)	08May37
5:17.0	Gladys Lunn (GBR)	07Aug37
5:15.3	Evelyne Forster (GBR)	22Jul39
5:11.0	Anne Oliver (GBR)	14Jun52
5:09.8	Enid Harding (GBR)	04Jul53
5:08.0	Anne Oliver (GBR)	12Sep53
5:02.6	Diane Leather (GBR)	30Sep53
5:00.3	Edith Treybal (ROM)	01Nov53
5:00.2	Diane Leather (GBR)	26May54
4:59.6	Diane Leather (GBR)	29May54
4:50.8	Diane Leather (GBR)	24May55
4:45.0	Diane Leather (GBR)	21Sep55
4:41.4	Marise Chamberlain (NZL)	08Dec62
4:39.2	Anne Smith (GBR)	13May67
4:37.0	Anne Smith (GBR)	03Jun67
4:36.8	Maria Gommers (HOL)	14Jun69
4:35.3	Ellen Tittel (FRG)	20Aug71
4:34.9	Glenda Reiser (CAN)	07Jul73
4:29.5	Paola Pigni-Cacchi (ITA)	08Aug73
4:23.8	Natalia Marasescu (ROM)	21May77
4:22.1	Natalia Marasescu (ROM)	27Jan79
4:21.7	Mary Decker (USA)	26Jan80
4:20.89	Lyudmila Veselkova (SOV)	12Sep81
4:18.08	Mary Decker-Tabb (USA)	09Jul82
4:17.44	Maricica Puica (ROM)	16Sep82
4:15.8	Natalya Artyomova (SOV)	05Aug84
4:16.71	Mary Decker-Slaney (USA)	21Aug85
4:15.61	Paula Ivan (ROM)	10Jul89
4:12.56	Svetlana Masterkova (RUS)	14Aug96

Topic: Geometry of Linear Maps

The pictures below contrast $f_{1}(x)=e^{x}$ and $f_{2}(x)=x^{2}$, which are nonlinear, with $h_{1}(x)=2x$ and $h_{2}(x)=-x$, which are linear. Each of the four pictures shows the domain $\mathbb {R} ^{1}$ on the left mapped to the codomain $\mathbb {R} ^{1}$ on the right. Arrows trace out where each map sends $x=0$, $x=1$, $x=2$, $x=-1$, and $x=-2$. Note how the nonlinear maps distort the domain in transforming it into the range. For instance, $f_{1}(1)$ is further from $f_{1}(2)$ than it is from $f_{1}(0)$ — the map is spreading the domain out unevenly so that an interval near $x=2$ is spread apart more than is an interval near $x=0$ when they are carried over to the range.

The linear maps are nicer, more regular, in that for each map all of the domain is spread by the same factor.

The only linear maps from $\mathbb {R} ^{1}$ to $\mathbb {R} ^{1}$ are multiplications by a scalar. In higher dimensions more can happen. For instance, this linear transformation of $\mathbb {R} ^{2}$, rotates vectors counterclockwise, and is not just a scalar multiplication.

The transformation of $\mathbb {R} ^{3}$ which projects vectors into the $xz$-plane is also not just a rescaling.

Nonetheless, even in higher dimensions the situation isn't too complicated.

Below, we use the standard bases to represent each linear map $h:\mathbb {R} ^{n}\to \mathbb {R} ^{m}$ by a matrix $H$. Recall that any $H$ can be factored $H=PBQ$, where $P$ and $Q$ are nonsingular and $B$ is a partial-identity matrix. Further, recall that nonsingular matrices factor into elementary matrices $PBQ=T_{n}T_{n-1}\cdots T_{j}BT_{j-1}\cdots T_{1}$, which are matrices that are obtained from the identity $I$ with one Gaussian step

$I{\xrightarrow[{}]{k\rho _{i}}}M_{i}(k)\qquad I{\xrightarrow[{}]{\rho _{i}\leftrightarrow \rho _{j}}}P_{i,j}\qquad I{\xrightarrow[{}]{k\rho _{i}+\rho _{j}}}C_{i,j}(k)$

($i\neq j$, $k\neq 0$). So if we understand the effect of a linear map described by a partial-identity matrix, and the effect of linear mapss described by the elementary matrices, then we will in some sense understand the effect of any linear map. (The pictures below stick to transformations of $\mathbb {R} ^{2}$ for ease of drawing, but the statements hold for maps from any $\mathbb {R} ^{n}$ to any $\mathbb {R} ^{m}$.)

The geometric effect of the linear transformation represented by a partial-identity matrix is projection.

${\begin{pmatrix}x\\y\\z\end{pmatrix}}\quad {\xrightarrow {{\begin{pmatrix}1&0&0\\0&1&0\\0&0&0\end{pmatrix}}_{{\mathcal {E}}_{3},{\mathcal {E}}_{3}}}}\quad {\begin{pmatrix}x\\y\\0\end{pmatrix}}$

For the $M_{i}(k)$ matrices, the geometric action of a transformation represented by such a matrix (with respect to the standard basis) is to stretch vectors by a factor of $k$ along the $i$-th axis. This map stretches by a factor of $3$ along the $x$-axis.

Note that if $0\leq k<1$ or if $k<0$ then the $i$-th component goes the other way; here, toward the left.

Either of these is a dilation.

The action of a transformation represented by a $P_{i,j}$ permutation matrix is to interchange the $i$-th and $j$-th axes; this is a particular kind of reflection.

In higher dimensions, permutations involving many axes can be decomposed into a combination of swaps of pairs of axes— see Problem 5.

The remaining case is that of matrices of the form $C_{i,j}(k)$. Recall that, for instance, that $C_{1,2}(2)$ performs $2\rho _{1}+\rho _{2}$.

${\begin{pmatrix}x\\y\end{pmatrix}}{\xrightarrow {{\begin{pmatrix}1&0\\2&1\end{pmatrix}}_{{\mathcal {E}}_{2},{\mathcal {E}}_{2}}}}\qquad {\begin{pmatrix}x\\2x+y\end{pmatrix}}$

In the picture below, the vector ${\vec {u}}$ with the first component of $1$ is affected less than the vector ${\vec {v}}$ with the first component of $2$— $h({\vec {u}})$ is only $2$ higher than ${\vec {u}}$ while $h({\vec {v}})$ is $4$ higher than ${\vec {v}}$.

Any vector with a first component of $1$ would be affected as is ${\vec {u}}$; it would be slid up by $2$. And any vector with a first component of $2$ would be slid up $4$, as was ${\vec {v}}$. That is, the transformation represented by $C_{i,j}(k)$ affects vectors depending on their $i$-th component.

Another way to see this same point is to consider the action of this map on the unit square. In the next picture, vectors with a first component of $0$, like the origin, are not pushed vertically at all but vectors with a positive first component are slid up. Here, all vectors with a first component of $1$— the entire right side of the square— is affected to the same extent. More generally, vectors on the same vertical line are slid up the same amount, namely, they are slid up by twice their first component. The resulting shape, a rhombus, has the same base and height as the square (and thus the same area) but the right angles are gone.

For contrast the next picture shows the effect of the map represented by $C_{2,1}(1)$. In this case, vectors are affected according to their second component. The vector ${\binom {x}{y}}$ is slid horozontally by twice $y$.

Because of this action, this kind of map is called a shear.

With that, we have covered the geometric effect of the four types of components in the expansion $H=T_{n}T_{n-1}\cdots T_{j}BT_{j-1}\cdots T_{1}$, the partial-identity projection $B$ and the elementary $T_{i}$'s. Since we understand its components, we in some sense understand the action of any $H$. As an illustration of this assertion, recall that under a linear map, the image of a subspace is a subspace and thus the linear transformation $h$ represented by $H$ maps lines through the origin to lines through the origin. (The dimension of the image space cannot be greater than the dimension of the domain space, so a line can't map onto, say, a plane.) We will extend that to show that any line, not just those through the origin, is mapped by $h$ to a line. The proof is simply that the partial-identity projection $B$ and the elementary $T_{i}$'s each turn a line input into a line output (verifying the four cases is Problem 6), and therefore their composition also preserves lines. Thus, by understanding its components we can understand arbitrary square matrices $H$, in the sense that we can prove things about them.

An understanding of the geometric effect of linear transformations on $\mathbb {R} ^{n}$ is very important in mathematics. Here is a familiar application from calculus. On the left is a picture of the action of the nonlinear function $y(x)=x^{2}+x$. As at that start of this Topic, overall the geometric effect of this map is irregular in that at different domain points it has different effects (e.g., as the domain point $x$ goes from $2$ to $-2$, the associated range point $f(x)$ at first decreases, then pauses instantaneously, and then increases).

But in calculus we don't focus on the map overall, we focus instead on the local effect of the map.

At $x=1$ the derivative is $y^{\prime }(1)=3$, so that near $x=1$ we have $\Delta y\approx 3\cdot \Delta x$.

That is, in a neighborhood of $x=1$, in carrying the domain to the codomain this map causes it to grow by a factor of $3$ — it is, locally, approximately, a dilation.

The picture below shows a small interval in the domain $(x-\Delta x\,..\,x+\Delta x)$ carried over to an interval in the codomain $(y-\Delta y\,..\,y+\Delta y)$ that is three times as wide: $\Delta y\approx 3\cdot \Delta x$.

(When the above picture is drawn in the traditional cartesian way then the prior sentence about the rate of growth of $y(x)$ is usually stated: the derivative $y^{\prime }(1)=3$ gives the slope of the line tangent to the graph at the point $(1,2)$.)

In higher dimensions, the idea is the same but the approximation is not just the $\mathbb {R} ^{1}$-to-$\mathbb {R} ^{1}$ scalar multiplication case. Instead, for a function $y:\mathbb {R} ^{n}\to \mathbb {R} ^{m}$ and a point ${\vec {x}}\in \mathbb {R} ^{n}$, the derivative is defined to be the linear map $h:\mathbb {R} ^{n}\to \mathbb {R} ^{m}$ best approximating how $y$ changes near $y({\vec {x}})$. So the geometry studied above applies.

We will close this Topic by remarking how this point of view makes clear an often-misunderstood, but very important, result about derivatives: the derivative of the composition of two functions is computed by using the Chain Rule for combining their derivatives. Recall that (with suitable conditions on the two functions)

${\frac {d\,(g\circ f)}{dx}}(x)={\frac {dg}{dx}}(f(x))\cdot {\frac {df}{dx}}(x)$

so that, for instance, the derivative of $\sin(x^{2}+3x)$ is $\cos(x^{2}+3x)\cdot (2x+3)$. How does this combination arise? From this picture of the action of the composition.

The first map $f$ dilates the neighborhood of $x$ by a factor of

${\frac {df}{dx}}(x)$

and the second map $g$ dilates some more, this time dilating a neighborhood of $f(x)$ by a factor of

${\frac {dg}{dx}}(\,f(x)\,)$

and as a result, the composition dilates by the product of these two.

In higher dimensions the map expressing how a function changes near a point is a linear map, and is expressed as a matrix. (So we understand the basic geometry of higher-dimensional derivatives; they are compositions of dilations, interchanges of axes, shears, and a projection). And, the Chain Rule just multiplies the matrices.

Thus, the geometry of linear maps $h:\mathbb {R} ^{n}\to \mathbb {R} ^{m}$ is appealing both for its simplicity and for its usefulness.

Exercises

Problem 1

Let $h:\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ be the transformation that rotates vectors clockwise by $\pi /4$ radians.

1. Find the matrix $H$ representing $h$ with respect to the standard bases. Use Gauss' method to reduce $H$ to the identity.
2. Translate the row reduction to to a matrix equation $T_{j}T_{j-1}\cdots T_{1}H=I$ (the prior item shows both that $H$ is similar to $I$, and that no column operations are needed to derive $I$ from $H$).
3. Solve this matrix equation for $H$.
4. Sketch the geometric effect matrix, that is, sketch how $H$ is expressed as a combination of dilations, flips, skews, and projections (the identity is a trivial projection).

Problem 2

What combination of dilations, flips, skews, and projections produces a rotation counterclockwise by $2\pi /3$ radians?

Problem 3

What combination of dilations, flips, skews, and projections produces the map $h:\mathbb {R} ^{3}\to \mathbb {R} ^{3}$ represented with respect to the standard bases by this matrix?

${\begin{pmatrix}1&2&1\\3&6&0\\1&2&2\end{pmatrix}}$

Problem 4

Show that any linear transformation of $\mathbb {R} ^{1}$ is the map that multiplies by a scalar $x\mapsto kx$.

Problem 5

Show that for any permutation (that is, reordering) $p$ of the numbers $1$, ..., $n$, the map

${\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}\mapsto {\begin{pmatrix}x_{p(1)}\\x_{p(2)}\\\vdots \\x_{p(n)}\end{pmatrix}}$

can be accomplished with a composition of maps, each of which only swaps a single pair of coordinates. Hint: it can be done by induction on $n$. (Remark: in the fourth chapter we will show this and we will also show that the parity of the number of swaps used is determined by $p$. That is, although a particular permutation could be accomplished in two different ways with two different numbers of swaps, either both ways use an even number of swaps, or both use an odd number.)

Problem 6

Show that linear maps preserve the linear structures of a space.

1. Show that for any linear map from $\mathbb {R} ^{n}$ to $\mathbb {R} ^{m}$, the image of any line is a line. The image may be a degenerate line, that is, a single point.
2. Show that the image of any linear surface is a linear surface. This generalizes the result that under a linear map the image of a subspace is a subspace.
3. Linear maps preserve other linear ideas. Show that linear maps preserve "betweeness": if the point $B$ is between $A$ and $C$ then the image of $B$ is between the image of $A$ and the image of $C$.

Problem 7

Use a picture like the one that appears in the discussion of the Chain Rule to answer: if a function $f:\mathbb {R} \to \mathbb {R}$ has an inverse, what's the relationship between how the function — locally, approximately — dilates space, and how its inverse dilates space (assuming, of course, that it has an inverse)?

Topic: Markov Chains

Here is a simple game: a player bets on coin tosses, a dollar each time, and the game ends either when the player has no money left or is up to five dollars. If the player starts with three dollars, what is the chance that the game takes at least five flips? Twenty-five flips?

At any point, this player has either $0, or $1, ..., or $5. We say that the player is in the state $s_{0}$, $s_{1}$, ..., or $s_{5}$. A game consists of moving from state to state. For instance, a player now in state $s_{3}$ has on the next flip a $0.5$ chance of moving to state $s_{2}$ and a $0.5$ chance of moving to $s_{4}$. The boundary states are a bit different; once in state $s_{0}$ or stat $s_{5}$, the player never leaves.

Let $p_{i}(n)$ be the probability that the player is in state $s_{i}$ after $n$ flips. Then, for instance, we have that the probability of being in state $s_{0}$ after flip $n+1$ is $p_{0}(n+1)=p_{0}(n)+0.5\cdot p_{1}(n)$. This matrix equation summarizes.

${\begin{pmatrix}1&0.5&0&0&0&0\\0.5&0&0.5&0&0&0\\0&0.5&0&0.5&0&0\\0&0&0.5&0&0.5&0\\0&0&0&0.5&0&0.5\\0&0&0&0&0.5&1\end{pmatrix}}{\begin{pmatrix}p_{0}(n)\\p_{1}(n)\\p_{2}(n)\\p_{3}(n)\\p_{4}(n)\\p_{5}(n)\end{pmatrix}}={\begin{pmatrix}p_{0}(n+1)\\p_{1}(n+1)\\p_{2}(n+1)\\p_{3}(n+1)\\p_{4}(n+1)\\p_{5}(n+1)\end{pmatrix}}$

With the initial condition that the player starts with three dollars, calculation gives this.

$n=0$	$n=1$	$n=2$	$n=3$	$n=4$	$\cdots$	$n=24$
${\begin{pmatrix}0\\0\\0\\1\\0\\0\end{pmatrix}}$	${\begin{pmatrix}0\\0\\0.5\\0\\0.5\\0\end{pmatrix}}$	${\begin{pmatrix}0\\0.25\\0\\0.5\\0\\0.25\end{pmatrix}}$	${\begin{pmatrix}0.125\\0\\0.375\\0\\0.25\\0.25\end{pmatrix}}$	${\begin{pmatrix}0.125\\0.1875\\0\\0.3125\\0\\0.375\end{pmatrix}}$	$\cdots$	${\begin{pmatrix}0.39600\\0.00276\\0\\0.00447\\0\\0.59676\end{pmatrix}}$

As this computational exploration suggests, the game is not likely to go on for long, with the player quickly ending in either state $s_{0}$ or state $s_{5}$. For instance, after the fourth flip there is a probability of $0.50$ that the game is already over. (Because a player who enters either of the boundary states never leaves, they are said to be absorbing.)

This game is an example of a Markov chain, named for A.A. Markov, who worked in the first half of the 1900's. Each vector of $p$'s is a probability vector and the matrix is a transition matrix. The notable feature of a Markov chain model is that it is historyless in that with a fixed transition matrix, the next state depends only on the current state, not on any prior states. Thus a player, say, who arrives at $s_{2}$ by starting in state $s_{3}$, then going to state $s_{2}$, then to $s_{1}$, and then to $s_{2}$ has at this point exactly the same chance of moving next to state $s_{3}$ as does a player whose history was to start in $s_{3}$, then go to $s_{4}$, and to $s_{3}$, and then to $s_{2}$.

Here is a Markov chain from sociology. A study (Macdonald & Ridge 1988, p. 202) divided occupations in the United Kingdom into upper level (executives and professionals), middle level (supervisors and skilled manual workers), and lower level (unskilled). To determine the mobility across these levels in a generation, about two thousand men were asked, "At which level are you, and at which level was your father when you were fourteen years old?" This equation summarizes the results.

${\begin{pmatrix}0.60&0.29&0.16\\0.26&0.37&0.27\\0.14&0.34&0.57\end{pmatrix}}{\begin{pmatrix}p_{U}(n)\\p_{M}(n)\\p_{L}(n)\end{pmatrix}}={\begin{pmatrix}p_{U}(n+1)\\p_{M}(n+1)\\p_{L}(n+1)\end{pmatrix}}$

For instance, a child of a lower class worker has a $.27$ probability of growing up to be middle class. Notice that the Markov model assumption about history seems reasonable— we expect that while a parent's occupation has a direct influence on the occupation of the child, the grandparent's occupation has no such direct influence. With the initial distribution of the respondents's fathers given below, this table lists the distributions for the next five generations.

$n=0$	$n=1$	$n=2$	$n=3$	$n=4$	$n=5$
${\begin{pmatrix}0.12\\0.32\\0.56\end{pmatrix}}$	${\begin{pmatrix}0.23\\0.34\\0.42\end{pmatrix}}$	${\begin{pmatrix}0.29\\0.34\\0.37\end{pmatrix}}$	${\begin{pmatrix}0.31\\0.34\\0.35\end{pmatrix}}$	${\begin{pmatrix}0.32\\0.33\\0.34\end{pmatrix}}$	${\begin{pmatrix}0.33\\0.33\\0.34\end{pmatrix}}$

One more example, from a very important subject, indeed. The World Series of American baseball is played between the team winning the American League and the team winning the National League (we follow [Brunner] but see also [Woodside]). The series is won by the first team to win four games. That means that a series is in one of twenty-four states: 0-0 (no games won yet by either team), 1-0 (one game won for the American League team and no games for the National League team), etc. If we assume that there is a probability $p$ that the American League team wins each game then we have the following transition matrix.

${\begin{pmatrix}0&0&0&0&\ldots \\p&0&0&0&\ldots \\1-p&0&0&0&\ldots \\0&p&0&0&\ldots \\0&1-p&p&0&\ldots \\0&0&1-p&0&\ldots \\\vdots &\vdots &\vdots &\vdots \end{pmatrix}}{\begin{pmatrix}p_{\text{0-0}}(n)\\p_{\text{1-0}}(n)\\p_{\text{0-1}}(n)\\p_{\text{2-0}}(n)\\p_{\text{1-1}}(n)\\p_{\text{0-2}}(n)\\\vdots \end{pmatrix}}={\begin{pmatrix}p_{\text{0-0}}(n+1)\\p_{\text{1-0}}(n+1)\\p_{\text{0-1}}(n+1)\\p_{\text{2-0}}(n+1)\\p_{\text{1-1}}(n+1)\\p_{\text{0-2}}(n+1)\\\vdots \end{pmatrix}}$

An especially interesting special case is $p=0.50$; this table lists the resulting components of the $n=0$ through $n=7$ vectors. (The code to generate this table in the computer algebra system Octave follows the exercises.)

	$n=0$	$n=1$	$n=2$	$n=3$	$n=4$	$n=5$	$n=6$	$n=7$
0-0	1	0	0	0	0	0	0	0
1-0	0	0.5	0	0	0	0	0	0
0-1	0	0.5	0	0	0	0	0	0
2-0	0	0	0.25	0	0	0	0	0
1-1	0	0	0.5	0	0	0	0	0
0-2	0	0	0.25	0	0	0	0	0
3-0	0	0	0	0.125	0	0	0	0
2-1	0	0	0	0.325	0	0	0	0
1-2	0	0	0	0.325	0	0	0	0
0-3	0	0	0	0.125	0	0	0	0
4-0	0	0	0	0	0.0625	0.0625	0.0625	0.0625
3-1	0	0	0	0	0.25	0	0	0
2-2	0	0	0	0	0.375	0	0	0
1-3	0	0	0	0	0.25	0	0	0
0-4	0	0	0	0	0.0625	0.0625	0.0625	0.0625
4-1	0	0	0	0	0	0.125	0.125	0.125
3-2	0	0	0	0	0	0.3125	0	0
2-3	0	0	0	0	0	0.3125	0	0
1-4	0	0	0	0	0	0.125	0.125	0.125
4-2	0	0	0	0	0	0	0.15625	0.15625
3-3	0	0	0	0	0	0	0.3125	0
2-4	0	0	0	0	0	0	0.15625	0.15625
4-3	0	0	0	0	0	0	0	0.15625
3-4	0	0	0	0	0	0	0	0.15625

Note that evenly-matched teams are likely to have a long series— there is a probability of $0.625$ that the series goes at least six games.

One reason for the inclusion of this Topic is that Markov chains are one of the most widely-used applications of matrix operations. Another reason is that it provides an example of the use of matrices where we do not consider the significance of the maps represented by the matrices. For more on Markov chains, there are many sources such as (Kemeny & Snell 1960) and (Iosifescu 1980).

Exercises

Use a computer for these problems. You can, for instance, adapt the Octave script given below.

Problem 1

These questions refer to the coin-flipping game.

1. Check the computations in the table at the end of the first paragraph.
2. Consider the second row of the vector table. Note that this row has alternating $0$'s. Must $p_{1}(j)$ be $0$ when $j$ is odd? Prove that it must be, or produce a counterexample.
3. Perform a computational experiment to estimate the chance that the player ends at five dollars, starting with one dollar, two dollars, and four dollars.

Problem 2

We consider throws of a die, and say the system is in state $s_{i}$ if the largest number yet appearing on the die was $i$.

1. Give the transition matrix.
2. Start the system in state $s_{1}$, and run it for five throws. What is the vector at the end?

(Feller 1968, p. 424)

Problem 3

There has been much interest in whether industries in the United States are moving from the Northeast and North Central regions to the South and West, motivated by the warmer climate, by lower wages, and by less unionization. Here is the transition matrix for large firms in Electric and Electronic Equipment (Kelton 1983, p. 43)

	NE	NC	S	W	Z
NE	0.787	0	0	0.111	0.102
NC	0	0.966	0.034	0	0
S	0	0.063	0.937	0	0
W	0	0	0.074	0.612	0.314
Z	0.021	0.009	0.005	0.010	0.954

For example, a firm in the Northeast region will be in the West region next year with probability $0.111$. (The Z entry is a "birth-death" state. For instance, with probability $0.102$ a large Electric and Electronic Equipment firm from the Northeast will move out of this system next year: go out of business, move abroad, or move to another category of firm. There is a $0.021$ probability that a firm in the National Census of Manufacturers will move into Electronics, or be created, or move in from abroad, into the Northeast. Finally, with probability $0.954$ a firm out of the categories will stay out, according to this research.)

1. Does the Markov model assumption of lack of history seem justified?
2. Assume that the initial distribution is even, except that the value at $Z$ is $0.9$. Compute the vectors for $n=1$ through $n=4$.
3. Suppose that the initial distribution is this.

   NE	NC	S	W	Z
   0.0000	0.6522	0.3478	0.0000	0.0000

   Calculate the distributions for $n=1$ through $n=4$.

4. Find the distribution for $n=50$ and $n=51$. Has the system settled down to an equilibrium?

Problem 4

This model has been suggested for some kinds of learning (Wickens 1982, p. 41). The learner starts in an undecided state $s_{U}$. Eventually the learner has to decide to do either response $A$ (that is, end in state $s_{A}$) or response $B$ (ending in $s_{B}$). However, the learner doesn't jump right from being undecided to being sure $A$ is the correct thing to do (or $B$). Instead, the learner spends some time in a "tentative-$A$" state, or a "tentative-$B$" state, trying the response out (denoted here $t_{A}$ and $t_{B}$). Imagine that once the learner has decided, it is final, so once $s_{A}$ or $s_{B}$ is entered it is never left. For the other state changes, imagine a transition is made with probability $p$ in either direction.

1. Construct the transition matrix.
2. Take $p=0.25$ and take the initial vector to be $1$ at $s_{U}$. Run this for five steps. What is the chance of ending up at $s_{A}$?
3. Do the same for $p=0.20$.
4. Graph $p$ versus the chance of ending at $s_{A}$. Is there a threshold value for $p$, above which the learner is almost sure not to take longer than five steps?

Problem 5

A certain town is in a certain country (this is a hypothetical problem). Each year ten percent of the town dwellers move to other parts of the country. Each year one percent of the people from elsewhere move to the town. Assume that there are two states $s_{T}$, living in town, and $s_{C}$, living elsewhere.

1. Construct the transistion matrix.
2. Starting with an initial distribution $s_{T}=0.3$ and $s_{C}=0.7$, get the results for the first ten years.
3. Do the same for $s_{T}=0.2$.
4. Are the two outcomes alike or different?

Problem 6

For the World Series application, use a computer to generate the seven vectors for $p=0.55$ and $p=0.6$.

1. What is the chance of the National League team winning it all, even though they have only a probability of $0.45$ or $0.40$ of winning any one game?
2. Graph the probability $p$ against the chance that the American League team wins it all. Is there a threshold value— a $p$ above which the better team is essentially ensured of winning?

(Some sample code is included below.)

Problem 7

A Markov matrix has each entry positive and each column sums to $1$.

1. Check that the three transistion matrices shown in this Topic meet these two conditions. Must any transition matrix do so?
2. Observe that if $A{\vec {v}}_{0}={\vec {v}}_{1}$ and $A{\vec {v}}_{1}={\vec {v}}_{2}$ then $A^{2}$ is a transition matrix from ${\vec {v}}_{0}$ to ${\vec {v}}_{2}$. Show that a power of a Markov matrix is also a Markov matrix.
3. Generalize the prior item by proving that the product of two appropriately-sized Markov matrices is a Markov matrix.

Solutions

Computer Code

This script markov.m for the computer algebra system Octave was used to generate the table of World Series outcomes. (The sharp character # marks the rest of a line as a comment.)

# Octave script file to compute chance of World Series outcomes.
function w = markov(p,v)
q = 1-p;
A=[0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 0-0
p,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 1-0
q,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 0-1_
0,p,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 2-0
0,q,p,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 1-1
0,0,q,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 0-2__
0,0,0,p,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 3-0
0,0,0,q,p,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 2-1
0,0,0,0,q,p, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 1-2_
0,0,0,0,0,q, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 0-3
0,0,0,0,0,0, p,0,0,0,1,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 4-0
0,0,0,0,0,0, q,p,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 3-1__
0,0,0,0,0,0, 0,q,p,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 2-2
0,0,0,0,0,0, 0,0,q,p,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0;  # 1-3
0,0,0,0,0,0, 0,0,0,q,0,0, 0,0,1,0,0,0, 0,0,0,0,0,0;  # 0-4_
0,0,0,0,0,0, 0,0,0,0,0,p, 0,0,0,1,0,0, 0,0,0,0,0,0;  # 4-1
0,0,0,0,0,0, 0,0,0,0,0,q, p,0,0,0,0,0, 0,0,0,0,0,0;  # 3-2
0,0,0,0,0,0, 0,0,0,0,0,0, q,p,0,0,0,0, 0,0,0,0,0,0;  # 2-3__
0,0,0,0,0,0, 0,0,0,0,0,0, 0,q,0,0,0,0, 1,0,0,0,0,0;  # 1-4
0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,p,0, 0,1,0,0,0,0;  # 4-2
0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,q,p, 0,0,0,0,0,0;  # 3-3_
0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,q, 0,0,0,1,0,0;  # 2-4
0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,p,0,1,0;  # 4-3
0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,0,0,0,0, 0,0,q,0,0,1]; # 3-4
w = A * v;
endfunction

Then the Octave session was this.

> v0=[1;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0]
> p=.5
> v1=markov(p,v0)
> v2=markov(p,v1)
...

Translating to another computer algebra system should be easy— all have commands similar to these.

Topic: Orthonormal Matrices

In The Elements, Euclid considers two figures to be the same if they have the same size and shape. That is, the triangles below are not equal because they are not the same set of points. But they are congruent— essentially indistinguishable for Euclid's purposes— because we can imagine picking the plane up, sliding it over and rotating it a bit, although not warping or stretching it, and then putting it back down, to superimpose the first figure on the second. (Euclid never explicitly states this principle but he uses it often (Casey 1890).)

In modern terminology, "picking the plane up ..." means considering a map from the plane to itself. Euclid has limited consideration to only certain transformations of the plane, ones that may possibly slide or turn the plane but not bend or stretch it. Accordingly, we define a map $f:\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ to be distance-preserving or a rigid motion or an isometry, if for all points $P_{1},P_{2}\in \mathbb {R} ^{2}$, the distance from $f(P_{1})$ to $f(P_{2})$ equals the distance from $P_{1}$ to $P_{2}$. We also define a plane figure to be a set of points in the plane and we say that two figures are congruent if there is a distance-preserving map from the plane to itself that carries one figure onto the other.

Many statements from Euclidean geometry follow easily from these definitions. Some are: (i) collinearity is invariant under any distance-preserving map (that is, if $P_{1}$, $P_{2}$, and $P_{3}$ are collinear then so are $f(P_{1})$, $f(P_{2})$, and $f(P_{3})$), (ii) betweeness is invariant under any distance-preserving map (if $P_{2}$ is between $P_{1}$ and $P_{3}$ then so is $f(P_{2})$ between $f(P_{1})$ and $f(P_{3})$), (iii) the property of being a triangle is invariant under any distance-preserving map (if a figure is a triangle then the image of that figure is also a triangle), (iv) and the property of being a circle is invariant under any distance-preserving map. In 1872, F. Klein suggested that Euclidean geometry can be characterized as the study of properties that are invariant under these maps. (This forms part of Klein's Erlanger Program, which proposes the organizing principle that each kind of geometry— Euclidean, projective, etc.— can be described as the study of the properties that are invariant under some group of transformations. The word "group" here means more than just "collection", but that lies outside of our scope.)

We can use linear algebra to characterize the distance-preserving maps of the plane.

First, there are distance-preserving transformations of the plane that are not linear. The obvious example is this translation.

${\begin{pmatrix}x\\y\end{pmatrix}}\quad \mapsto \quad {\begin{pmatrix}x\\y\end{pmatrix}}+{\begin{pmatrix}1\\0\end{pmatrix}}={\begin{pmatrix}x+1\\y\end{pmatrix}}$

However, this example turns out to be the only example, in the sense that if $f$ is distance-preserving and sends ${\vec {0}}$ to ${\vec {v}}_{0}$ then the map ${\vec {v}}\mapsto f({\vec {v}})-{\vec {v}}_{0}$ is linear. That will follow immediately from this statement: a map $t$ that is distance-preserving and sends ${\vec {0}}$ to itself is linear. To prove this equivalent statement, let

$t({\vec {e}}_{1})={\begin{pmatrix}a\\b\end{pmatrix}}\qquad t({\vec {e}}_{2})={\begin{pmatrix}c\\d\end{pmatrix}}$

for some $a,b,c,d\in \mathbb {R}$. Then to show that $t$ is linear, we can show that it can be represented by a matrix, that is, that $t$ acts in this way for all $x,y\in \mathbb {R}$.

${\vec {v}}={\begin{pmatrix}x\\y\end{pmatrix}}{\stackrel {t}{\longmapsto }}{\begin{pmatrix}ax+cy\\bx+dy\end{pmatrix}}\qquad \qquad (*)$

Recall that if we fix three non-collinear points then any point in the plane can be described by giving its distance from those three. So any point ${\vec {v}}$ in the domain is determined by its distance from the three fixed points ${\vec {0}}$, ${\vec {e}}_{1}$, and ${\vec {e}}_{2}$. Similarly, any point $t({\vec {v}})$ in the codomain is determined by its distance from the three fixed points $t({\vec {0}})$, $t({\vec {e}}_{1})$, and $t({\vec {e}}_{2})$ (these three are not collinear because, as mentioned above, collinearity is invariant and ${\vec {0}}$, ${\vec {e}}_{1}$, and ${\vec {e}}_{2}$ are not collinear). In fact, because $t$ is distance-preserving, we can say more: for the point ${\vec {v}}$ in the plane that is determined by being the distance $d_{0}$ from ${\vec {0}}$, the distance $d_{1}$ from ${\vec {e}}_{1}$, and the distance $d_{2}$ from ${\vec {e}}_{2}$, its image $t({\vec {v}})$ must be the unique point in the codomain that is determined by being $d_{0}$ from $t({\vec {0}})$, $d_{1}$ from $t({\vec {e}}_{1})$, and $d_{2}$ from $t({\vec {e}}_{2})$. Because of the uniqueness, checking that the action in ($*$) works in the $d_{0}$, $d_{1}$, and $d_{2}$ cases

${\text{dist}}\,({\begin{pmatrix}x\\y\end{pmatrix}},{\vec {0}})={\text{dist}}\,(t({\begin{pmatrix}x\\y\end{pmatrix}}),t({\vec {0}}))={\text{dist}}\,({\begin{pmatrix}ax+cy\\bx+dy\end{pmatrix}},{\vec {0}})$

($t$ is assumed to send ${\vec {0}}$ to itself)

${\text{dist}}\,({\begin{pmatrix}x\\y\end{pmatrix}},{\vec {e}}_{1})={\text{dist}}\,(t({\begin{pmatrix}x\\y\end{pmatrix}}),t({\vec {e}}_{1}))={\text{dist}}\,({\begin{pmatrix}ax+cy\\bx+dy\end{pmatrix}},{\begin{pmatrix}a\\b\end{pmatrix}})$

and

${\text{dist}}\,({\begin{pmatrix}x\\y\end{pmatrix}},{\vec {e}}_{2})={\text{dist}}\,(t({\begin{pmatrix}x\\y\end{pmatrix}}),t({\vec {e}}_{2}))={\text{dist}}\,({\begin{pmatrix}ax+cy\\bx+dy\end{pmatrix}},{\begin{pmatrix}c\\d\end{pmatrix}})$

suffices to show that ($*$) describes $t$. Those checks are routine.

Thus, any distance-preserving $f:\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ can be written $f({\vec {v}})=t({\vec {v}})+{\vec {v}}_{0}$ for some constant vector ${\vec {v}}_{0}$ and linear map $t$ that is distance-preserving.

Not every linear map is distance-preserving, for example, ${\vec {v}}\mapsto 2{\vec {v}}$ does not preserve distances. But there is a neat characterization: a linear transformation $t$ of the plane is distance-preserving if and only if both $|t({\vec {e}}_{1})|=|t({\vec {e}}_{2})|=1$ and $t({\vec {e}}_{1})$ is orthogonal to $t({\vec {e}}_{2})$. The "only if" half of that statement is easy— because $t$ is distance-preserving it must preserve the lengths of vectors, and because $t$ is distance-preserving the Pythagorean theorem shows that it must preserve orthogonality. For the "if" half, it suffices to check that the map preserves lengths of vectors, because then for all ${\vec {p}}$ and ${\vec {q}}$ the distance between the two is preserved $|t({\vec {p}}-{\vec {q}}\,)|=|t({\vec {p}})-t({\vec {q}}\,)|=|{\vec {p}}-{\vec {q}}\,|$. For that check, let

${\vec {v}}={\begin{pmatrix}x\\y\end{pmatrix}}\quad t({\vec {e}}_{1})={\begin{pmatrix}a\\b\end{pmatrix}}\quad t({\vec {e}}_{2})={\begin{pmatrix}c\\d\end{pmatrix}}$

and, with the "if" assumptions that $a^{2}+b^{2}=c^{2}+d^{2}=1$ and $ac+bd=0$ we have this.

${\begin{array}{rl}|t({\vec {v}}\,)|^{2}&=(ax+cy)^{2}+(bx+dy)^{2}\\&=a^{2}x^{2}+2acxy+c^{2}y^{2}+b^{2}x^{2}+2bdxy+d^{2}y^{2}\\&=x^{2}(a^{2}+b^{2})+y^{2}(c^{2}+d^{2})+2xy(ac+bd)\\&=x^{2}+y^{2}\\&=|{\vec {v}}\,|^{2}\end{array}}$

One thing that is neat about this characterization is that we can easily recognize matrices that represent such a map with respect to the standard bases. Those matrices have that when the columns are written as vectors then they are of length one and are mutually orthogonal. Such a matrix is called an orthonormal matrix or orthogonal matrix (the first term is commonly used to mean not just that the columns are orthogonal, but also that they have length one).

We can use this insight to delimit the geometric actions possible in distance-preserving maps. Because $|t({\vec {v}}\,)|=|{\vec {v}}\,|$, any ${\vec {v}}$ is mapped by $t$ to lie somewhere on the circle about the origin that has radius equal to the length of ${\vec {v}}$. In particular, ${\vec {e}}_{1}$ and ${\vec {e}}_{2}$ are mapped to the unit circle. What's more, once we fix the unit vector ${\vec {e}}_{1}$ as mapped to the vector with components $a$ and $b$ then there are only two places where ${\vec {e}}_{2}$ can be mapped if that image is to be perpendicular to the first vector: one where ${\vec {e}}_{2}$ maintains its position a quarter circle clockwise from

${\vec {e}}_{1}$

        ${\rm {Rep}}_{{\mathcal {E}}_{2},{\mathcal {E}}_{2}}(t)={\begin{pmatrix}a&-b\\b&a\end{pmatrix}}$

and one where is is mapped a quarter circle counterclockwise.

        ${\rm {Rep}}_{{\mathcal {E}}_{2},{\mathcal {E}}_{2}}(t)={\begin{pmatrix}a&b\\b&-a\end{pmatrix}}$

We can geometrically describe these two cases. Let $\theta$ be the angle between the $x$-axis and the image of ${\vec {e}}_{1}$, measured counterclockwise. The first matrix above represents, with respect to the standard bases, a rotation of the plane by $\theta$ radians.

        ${\begin{pmatrix}x\\y\end{pmatrix}}{\stackrel {t}{\longmapsto }}{\begin{pmatrix}x\cos \theta -y\sin \theta \\x\sin \theta +y\cos \theta \end{pmatrix}}$

The second matrix above represents a reflection of the plane through the line bisecting the angle between ${\vec {e}}_{1}$ and $t({\vec {e}}_{1})$.

        ${\begin{pmatrix}x\\y\end{pmatrix}}{\stackrel {t}{\longmapsto }}{\begin{pmatrix}x\cos \theta +y\sin \theta \\x\sin \theta -y\cos \theta \end{pmatrix}}$

(This picture shows ${\vec {e}}_{1}$ reflected up into the first quadrant and ${\vec {e}}_{2}$ reflected down into the fourth quadrant.)

Note again: the angle between ${\vec {e}}_{1}$ and ${\vec {e}}_{2}$ runs counterclockwise, and in the first map above the angle from $t({\vec {e}}_{1})$ to $t({\vec {e}}_{2})$ is also counterclockwise, so the orientation of the angle is preserved. But in the second map the orientation is reversed. A distance-preserving map is direct if it preserves orientations and opposite if it reverses orientation.

So, we have characterized the Euclidean study of congruence: it considers, for plane figures, the properties that are invariant under combinations of (i) a rotation followed by a translation, or (ii) a reflection followed by a translation (a reflection followed by a non-trivial translation is a glide reflection).

Another idea, besides congruence of figures, encountered in elementary geometry is that figures are similar if they are congruent after a change of scale. These two triangles are similar since the second is the same shape as the first, but $3/2$-ths the size.

From the above work, we have that figures are similar if there is an orthonormal matrix $T$ such that the points ${\vec {q}}$ on one are derived from the points ${\vec {p}}$ by ${\vec {q}}=(kT){\vec {v}}+{\vec {p}}_{0}$ for some nonzero real number $k$ and constant vector ${\vec {p}}_{0}$.

Although many of these ideas were first explored by Euclid, mathematics is timeless and they are very much in use today. One application of the maps studied above is in computer graphics. We can, for example, animate this top view of a cube by putting together film frames of it rotating; that's a rigid motion.

Frame 1	Frame 2	Frame 3

We could also make the cube appear to be moving away from us by producing film frames of it shrinking, which gives us figures that are similar.

Frame 1:	Frame 2:	Frame 3:

Computer graphics incorporates techniques from linear algebra in many other ways (see Problem 4).

So the analysis above of distance-preserving maps is useful as well as interesting. A beautiful book that explores some of this area is (Weyl 1952). More on groups, of transformations and otherwise, can be found in any book on Modern Algebra, for instance (Birkhoff & MacLane 1965). More on Klein and the Erlanger Program is in (Yaglom 1988).

Exercises

Problem 1

Decide if each of these is an orthonormal matrix.

1. ${\begin{pmatrix}1/{\sqrt {2}}&-1/{\sqrt {2}}\\-1/{\sqrt {2}}&-1/{\sqrt {2}}\end{pmatrix}}$
2. ${\begin{pmatrix}1/{\sqrt {3}}&-1/{\sqrt {3}}\\-1/{\sqrt {3}}&-1/{\sqrt {3}}\end{pmatrix}}$
3. ${\begin{pmatrix}1/{\sqrt {3}}&-{\sqrt {2}}/{\sqrt {3}}\\-{\sqrt {2}}/{\sqrt {3}}&-1/{\sqrt {3}}\end{pmatrix}}$

Problem 2

Write down the formula for each of these distance-preserving maps.

1. the map that rotates $\pi /6$ radians, and then translates by ${\vec {e}}_{2}$
2. the map that reflects about the line $y=2x$
3. the map that reflects about $y=-2x$ and translates over $1$ and up $1$

Problem 3

1. The proof that a map that is distance-preserving and sends the zero vector to itself incidentally shows that such a map is one-to-one and onto (the point in the domain determined by $d_{0}$, $d_{1}$, and $d_{2}$ corresponds to the point in the codomain determined by those three). Therefore any distance-preserving map has an inverse. Show that the inverse is also distance-preserving.
2. Prove that congruence is an equivalence relation between plane figures.

Problem 4

In practice the matrix for the distance-preserving linear transformation and the translation are often combined into one. Check that these two computations yield the same first two components.

${\begin{pmatrix}a&c\\b&d\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}+{\begin{pmatrix}e\\f\end{pmatrix}}\qquad {\begin{pmatrix}a&c&e\\b&d&f\\0&0&1\end{pmatrix}}{\begin{pmatrix}x\\y\\1\end{pmatrix}}$

(These are homogeneous coordinates; see the Topic on Projective Geometry).

Problem 5

1. Verify that the properties described in the second paragraph of this Topic as invariant under distance-preserving maps are indeed so.
2. Give two more properties that are of interest in Euclidean geometry from your experience in studying that subject that are also invariant under distance-preserving maps.
3. Give a property that is not of interest in Euclidean geometry and is not invariant under distance-preserving maps.