Trigonometry/The Pythagorean Theorem
In a right triangle
The square of the hypotenuse
is equal to
the sum of the squares of the other two sides.
Khan Academy
[edit | edit source]Video Links
[edit | edit source]The Khan Academy has video material relating to this topic which you may find easier to follow:
- The Pythagorean Theorem, gives the theorem.
- Pythagorean Theorem II, has worked through exercise on this topic.
The Theorem
[edit | edit source]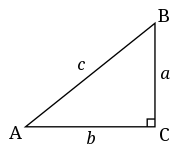
In a right triangle (right-angled triangle) the longest side is always furthest away from the right angle. It is called the hypotenuse. The length of the hypotenuse can be calculated from the lengths of the two other sides. In the diagram, c is the hypotenuse and we can calculate it from a and b.
This is a statement of the Pythagorean Theorem or Pythagoras' Theorem - as an equation relating the lengths of the sides a, b and c:[1]
where c represents the length of the hypotenuse, and a and b represent the lengths of the other two sides.
This only works for right triangles!
For the right angle triangle with corners labelled by A,B,C as shown, the following says the same thing:
All we've done here is just use a different notation for the sides a, b and c.
Geometrical Interpretation
[edit | edit source]
We can also show this equation with a diagram, as on the right, where each side of a right angle triangle has a square attached to it. This is the geometrical interpretation of the Pythagorean theorem, looking at the theorem as a theorem about areas. The areas of the smaller squares add up to the area of the larger square.
In terms of areas, the Pythagorean Theorem states:
In any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).
The two ways of talking about the Pythagorean theorem amount to exactly the same thing, since the area of a square is just the length of one side squared.
History of the Theorem
[edit | edit source]
The Pythagorean theorem is named after the Greek mathematician Pythagoras, who by tradition is credited with its discovery and proof,[2][3] although it is often argued that knowledge of the theorem predates him. There is much evidence that Babylonian mathematicians understood the formula.[4]
Three Worked Examples
[edit | edit source]In a right triangle
The square of the hypotenuse
is equal to
the sum of the squares of the other two sides.
|
Example 1 An often used example for the Pythagorean Theorem is a right triangle in which and because the numbers come out particularly nicely:
and and |
|
Example 2 Another often used example is a right triangle in which the two remaining angles are and both and . This time the answer doesn't come out as a whole number:
and and we can stop here, or else give the answer as a decimal. The symbol means 'approximately'. |
|
Example 3 One more example is a right triangle in which the shorter sides are cm and cm. What's this about and ? It really doesn't matter what letter we use to name the lengths of the sides as long as we are consistent. The formula in the blue box still holds. In this case we could call the hypotenuse , and so we have .
and
and giving the answer as a decimal.
Does the answer make sense?[edit | edit source]It's worth checking the answer makes some kind of sense. If the short sides are 11 cm and 7 cm is it reasonable that the long side is about 13 cm? Yes, it is. If you'd got an answer of 20 cm (or 170 cm) it would be unreasonable. The two other sides won't stretch that far. Or if the answer were 11 cm or less than you'd know that you hadn't got the length of the hypotenuse, the longest side. We're OK here with this answer of 13.04 cm, which we probably should round down to 13 cm. |
In 3D
[edit | edit source]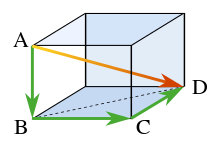
Pythagoras' theorem can be applied to three dimensions as follows.
Consider the rectangular solid shown in the figure. The length of diagonal BD along the floor of the rectangular solid is found from Pythagoras' theorem as:
where these three sides form a right triangle. Using horizontal diagonal BD and the vertical edge AB, the length of diagonal AD then is found by a second application of Pythagoras' theorem as:
or, doing it all in one step:
This result is the three-dimensional expression for the diagonal in terms of the three mutually perpendicular sides.
This one-step formula may be viewed as a generalization of Pythagoras' theorem to higher dimensions. However, this result is really just the repeated application of the original Pythagoras' theorem.
The Pyramid of Khafre
[edit | edit source]Other forms
[edit | edit source]As pointed out in the introduction, if c denotes the length of the hypotenuse and a and b denote the lengths of the other two sides, Pythagoras' theorem can be expressed as the Pythagorean equation:
or, solved for c:
That is what we have been doing in all the examples above. We are using the shorter sides to work out what the length of the hypotenuse is.
If the hypotenuse c is known, and the length of one of the legs must be found, the following equations can be used:
or
The Pythagorean equation provides a simple relation among the three sides of a right triangle so that if the lengths of any two sides are known, the length of the third side can be found.
Exercises
[edit | edit source]|
A cubical box is used to ship a printer. If one side is 90 cm, what is the longest distance between any two corners of the box? |
|
An LCD television screen is measured 26 inches from corner to corner. The screen height is 13 inches. How wide is the screen? (To one-tenth of an inch) |
|
|
Aliens from the fourth dimension are packing their holographic TV into a box ready for a trip to Earth. The box measures 1.5 Angstroms by 1.5 Angstroms by 1.5 Angstroms by 1.5 Angstroms (it is a 4 dimensional hypercube). What is the length of the longest diagonal? |
|
If a room is 17 ft long, 14 ft wide, and 10 ft high, what is the length of the diagonal of (a) the floor, (b) an end wall, and (c) a side wall of the room? |
|
Find the missing side (Pythagorean triples)
|
|
Squaring small numbers
|
References
[edit | edit source]- ↑ Judith D. Sally, Paul Sally (2007). "Chapter 3: Pythagorean triples". Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore. p. 63. ISBN 0821844032.
- ↑
George Johnston Allman (1889). Greek Geometry from Thales to Euclid (Reprinted by Kessinger Publishing LLC 2005 ed.). Hodges, Figgis, & Co. p. 26. ISBN 143260662X.
The discovery of the law of three squares, commonly called the "theorem of Pythagoras" is attributed to him by – amongst others – Vitruvius, Diogenes Laertius, Proclus, and Plutarch ...
- ↑ (Heath 1921, Vol I, p. 144)
- ↑
Otto Neugebauer (1969). The exact sciences in antiquity (Republication of 1957 Brown University Press 2nd ed.). Courier Dover Publications. p. 36. ISBN 0486223329.. For a different view, see Dick Teresi (2003). Lost Discoveries: The Ancient Roots of Modern Science. Simon and Schuster. p. 52. ISBN 074324379X., where the speculation is made that the first column of a tablet 322 in the Plimpton collection supports a Babylonian knowledge of some elements of trigonometry. That notion is pretty much laid to rest by Eleanor Robson (2002). "Words and Pictures: New Light on Plimpton 322". The American Mathematical Monthly. Mathematical Association of America. 109 (2): 105–120. doi:10.2307/2695324.
{{cite journal}}: Invalid|ref=harv(help) See also pdf file. The accepted view today is that the Babylonians had no awareness of trigonometric functions. See Abdulrahman A. Abdulaziz (2010). "The Plimpton 322 Tablet and the Babylonian Method of Generating Pythagorean Triples". ArXiv preprint.{{cite journal}}: Invalid|ref=harv(help) §2, page 7.




















































