Exponential
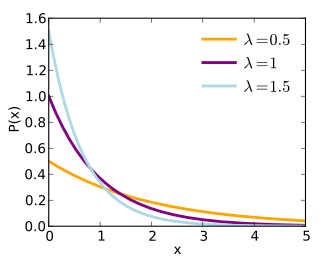
Probability density function
Cumulative distribution function
Parameters
λ > 0scale
Support
x ∈ [0, ∞)
PDF
λ e−λx
CDF
1 − e−λx
Mean
λ −1
Median
λ −1 ln 2
Mode
0
Variance
λ −2
Skewness
2
Ex. kurtosis
6
Entropy
1 − ln(λ )
MGF
(
1
−
t
λ
)
−
1
{\displaystyle \left(1-{\frac {t}{\lambda }}\right)^{-1}\,}
CF
(
1
−
i
t
λ
)
−
1
{\displaystyle \left(1-{\frac {it}{\lambda }}\right)^{-1}\,}
Exponential distribution refers to a statistical distribution used to model the time between independent events that happen at a constant average rate λ. Some examples of this distribution are:
The distance between one car passing by after the previous one.
The rate at which radioactive particles decay. For the stochastic variable X, probability distribution function of it is:
f
x
(
x
)
=
{
λ
e
−
λ
x
,
if
x
≥
0
0
,
if
x
<
0
{\displaystyle f_{x}(x)={\begin{cases}\lambda e^{-\lambda x},&{\mbox{if }}x\geq 0\\0,&{\mbox{if }}x<0\end{cases}}}
and the cumulative distribution function is:
F
x
(
x
)
=
{
0
,
if
x
<
0
1
−
e
−
λ
x
,
if
x
≥
0
{\displaystyle F_{x}(x)={\begin{cases}0,&{\mbox{if }}x<0\\{1-e^{-\lambda x}},&{\mbox{if }}x\geq 0\end{cases}}}
Exponential distribution is denoted as
X
∈
Exp(m)
{\displaystyle X\in {\mbox{Exp(m)}}}
We derive the mean as follows.
E
[
X
]
=
∫
−
∞
∞
x
⋅
f
(
x
)
d
x
{\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }x\cdot f(x)dx}
E
[
X
]
=
∫
0
∞
x
λ
e
−
λ
x
d
x
{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }x\lambda e^{-\lambda x}dx}
E
[
X
]
=
∫
0
∞
(
−
x
)
(
−
λ
e
−
λ
x
)
d
x
{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }(-x)(-\lambda e^{-\lambda x})dx}
We will use integration by parts with u=−x and v=e−λx . We see that du=-1 and dv=−λe−λx .
E
[
X
]
=
[
−
x
⋅
e
−
λ
x
]
0
∞
−
∫
0
∞
(
e
−
λ
x
)
(
−
1
)
d
x
{\displaystyle \operatorname {E} [X]=\left[-x\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-1)dx}
E
[
X
]
=
[
0
−
0
]
+
[
−
1
λ
(
e
−
λ
x
)
]
0
∞
{\displaystyle \operatorname {E} [X]=[0-0]+\left[{-1 \over \lambda }(e^{-\lambda x})\right]_{0}^{\infty }}
E
[
X
]
=
[
0
−
−
1
λ
]
{\displaystyle \operatorname {E} [X]=\left[0-{-1 \over \lambda }\right]}
E
[
X
]
=
1
λ
{\displaystyle \operatorname {E} [X]={1 \over \lambda }}
We use the following formula for the variance.
Var
(
X
)
=
E
[
X
2
]
−
(
E
[
X
]
)
2
{\displaystyle \operatorname {Var} (X)=\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}}
Var
(
X
)
=
∫
−
∞
∞
x
2
⋅
f
(
x
)
d
x
−
(
2
)
2
{\displaystyle \operatorname {Var} (X)=\int _{-\infty }^{\infty }x^{2}\cdot f(x)dx-\left({2}\right)^{2}}
Var
(
X
)
=
∫
0
∞
x
2
e
−
2
x
d
x
−
2
{\displaystyle \operatorname {Var} (X)=\int _{0}^{\infty }x^{2}e^{-2x}dx-{2}}
We'll use integration by parts with
u
=
−
x
2
{\displaystyle u=-x^{2}}
v
=
e
−
2
x
{\displaystyle v=e^{-2x}}
d
u
=
−
2
x
{\displaystyle du=-2x}
v
=
−
2
e
−
2
x
{\displaystyle v=-2e^{-2x}}
Var
(
X
)
=
{
[
−
x
2
⋅
e
−
λ
x
]
0
∞
−
∫
0
∞
(
e
−
λ
x
)
(
−
2
x
)
d
x
}
−
1
λ
2
{\displaystyle \operatorname {Var} (X)=\left\{\left[-x^{2}\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-2x)dx\right\}-{1 \over \lambda ^{2}}}
Var
(
X
)
=
[
0
−
0
]
+
2
λ
∫
0
∞
x
λ
e
−
λ
x
d
x
−
1
λ
2
{\displaystyle \operatorname {Var} (X)=[0-0]+{2 \over \lambda }\int _{0}^{\infty }x\lambda e^{-\lambda x}dx-{1 \over \lambda ^{2}}}
We see that the integral is just
E
[
X
]
{\displaystyle \operatorname {E} [X]}
Var
(
X
)
=
2
λ
1
λ
−
1
λ
2
{\displaystyle \operatorname {Var} (X)={2 \over \lambda }{1 \over \lambda }-{1 \over \lambda ^{2}}}
Var
(
X
)
=
1
λ
2
{\displaystyle \operatorname {Var} (X)={1 \over \lambda ^{2}}}






![{\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }x\cdot f(x)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c925eb7f3d99af3083ee5838c3bec6f3838997a)
![{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }x\lambda e^{-\lambda x}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de21e0e435a11373f8f68aa9365a100fd28434b7)
![{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }(-x)(-\lambda e^{-\lambda x})dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22e2936bccbe650f7919d6dfeb9db772d222f370)
![{\displaystyle \operatorname {E} [X]=\left[-x\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-1)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0a325796212c52d7cc34c2e57e5e0a5869121f)
![{\displaystyle \operatorname {E} [X]=[0-0]+\left[{-1 \over \lambda }(e^{-\lambda x})\right]_{0}^{\infty }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcfc71b113a0864019d9801c659d3ac3294525e2)
![{\displaystyle \operatorname {E} [X]=\left[0-{-1 \over \lambda }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcc46e6600d22129f1f8916bd6bcfa332679719e)
![{\displaystyle \operatorname {E} [X]={1 \over \lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf488e5f107cc237b5235226664cf3b1d5c02bcd)
![{\displaystyle \operatorname {Var} (X)=\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd5a922df13bdee788c0f06474fe002a42c25d8a)






![{\displaystyle \operatorname {Var} (X)=\left\{\left[-x^{2}\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-2x)dx\right\}-{1 \over \lambda ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aa497aeeb4e8301234482593735ec9726a74a95)
![{\displaystyle \operatorname {Var} (X)=[0-0]+{2 \over \lambda }\int _{0}^{\infty }x\lambda e^{-\lambda x}dx-{1 \over \lambda ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/620c93fc59bb00faabfa622a4b600f2a0dc8ac42)
![{\displaystyle \operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44dd294aa33c0865f58e2b1bdaf44ebe911dbf93)

